導氣式步槍單發精度仿真分析方法
苑大威,沙金龍,王雪皎
(1.瞬態沖擊技術重點實驗室,北京 102202;2.中國兵器工業第208研究所,北京 102202)
目前步槍射擊精度指標主要靠試驗獲取,現有的射擊精度仿真分析方法大多只考慮槍彈因素,無法在設計初期仿真分析精度指標,缺乏一種行之有效的射擊精度仿真分析方法用以指導設計。
隨著仿真技術的發展,研究人員相繼開展了槍械射擊精度仿真分析,李濤等[1-2]仿真分析了射頻、發射動力學對射擊精度的影響,王兆勝等[3-4]從試驗的角度分析了槍械射擊精度的影響因素、表征方法。上述仿真分析因素較為單一,需要進行更加系統、深入的研究。
本文主要研究固定架狀態步槍的單發射擊精度,研究中排除了人體因素的影響。本射擊精度仿真分析方法基于隨機內、外彈道方程,結合仿真分析,在考慮全槍和彈藥結構及參數的基礎上,研究影響射擊精度的隨機因素,在立靶散布上,獲得規定射程處R50、R100值(R50為半數彈著圓半徑,R100為全數彈著圓半徑),該方法可以用于指導槍械結構優化設計,達到提高射擊精度的目的。
1 射擊精度仿真分析方案
本文單發射擊精度仿真分析的具體方案為:將初速誤差、彈形系數誤差、射角誤差(包括橫向及縱向射角)等影響步槍射擊精度的因素融入到隨機外彈道方程[5](本研究聚焦槍械結構因素的影響,暫不考慮后效期影響產生的起始擾動和氣動跳角)。其中,彈形系數誤差來自加工尺寸公差要求;初速誤差來源于影響內彈道的裝藥量、彈丸質量、藥室容積、啟動壓力等隨機因素,通過融入隨機內彈道方程計算獲得;橫向及縱向射角誤差主要通過仿真分析提取,并進行試驗驗證;最終針對4個誤差變量建立概率密度函數數學模型,并輸入到隨機外彈道方程,可仿真分析出槍械射擊精度,獲得100 m處R50和R100值,并進行試驗驗證。方案流程如圖1所示。

圖1 導氣式步槍射擊精度仿真分析方案
2 彈丸初速誤差分析計算
彈丸初速誤差主要來源于影響內彈道的隨機因素,包括:裝藥量mc、彈丸質量mp、藥室容積V、啟動壓力p0[6-7]。將這些隨機量融入內彈道方程,建立隨機內彈道數學模型,設隨機變量X服從正態分布,即X~N(μ,σ2),概率密度函數:
(1)
則隨機量正態分布概率模型可用x=σ+μ得到,其中各隨機變量的均值為名義數值,標準差來自實際加工或工藝誤差,如表1所示。

表1 內彈道隨機變量
將這些隨機因素生成1 000組的組合作為隨機內彈道仿真的輸入,求解得到如圖2、圖3所示的最大膛壓及彈丸初速的隨機分布,圖中,ε為射彈數,最大膛壓均值為310 MPa,標準差為25 MPa;彈丸初速均值為910 m/s,標準差為20 m/s。
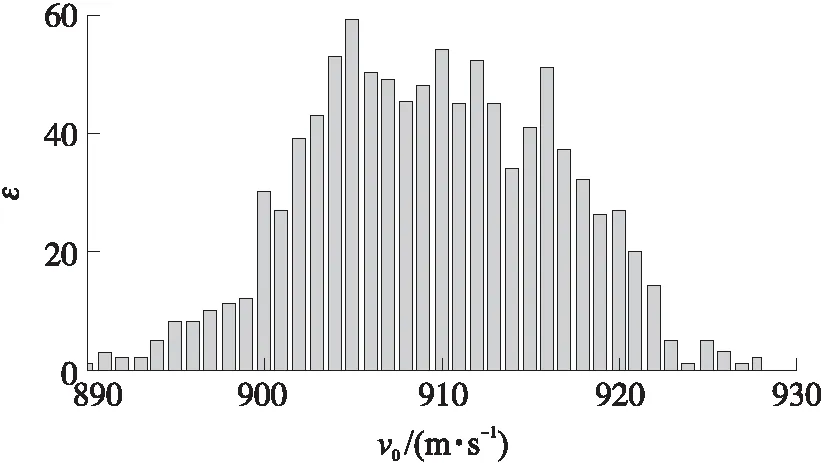
圖2 初速隨機分布
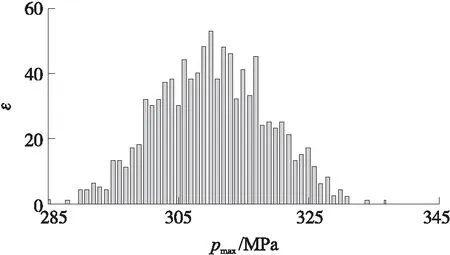
圖3 膛壓隨機分布
假設:①火藥燃燒服從幾何燃燒定律;②彈丸運動在平均壓力下進行;③膛壁熱散失忽略不計;④火藥燃燒生成物成分始終不變。內彈道方程如下:
(2)
式中:χ,μ為火藥形狀特征量;ψ為火藥已燃百分比;Ik為火藥燃燒結束瞬間壓力全沖量;φ為次要功系數;t為火藥燃燒時間;tq為彈丸經過導氣孔的時間;α為余容;lψ為藥室容積縮徑長;ζ=k-1,k為絕熱系數;B為時間參數;l為彈丸行程;β為導氣室結構參數;pq為導氣室壓力;pφ為彈丸經過導氣孔瞬間膛內火藥氣體壓力;n為燃速指數;μ1為燃速系數;e1為弧厚;e為藥粒已燃厚度;v為彈丸速度;p為平均壓力;Z為火藥已燃相對厚度;S為槍膛截面積;f為火藥力。
3 射角誤差仿真分析
射角誤差主要來源于槍管的振動和角位移,彈丸出槍口時槍管軸線與發射前產生一個小的角度。引起射角誤差的主要原因包括自動機運動和導氣壓力作用,可采用仿真的方法分析槍口的跳動量和位移量。
3.1 自動機運動下槍口跳動量分析
通過多體動力學軟件[8]分析全槍機構動作,仿真模型如圖4所示。槍托和護手設置固定約束,膛底施加膛壓曲線,采用剛柔耦合的方法將槍管柔性化,獲得槍口跳動量值,槍口橫向最大跳動量為0.02 mm,槍口縱向最大跳動量為0.08 mm。

圖4 全槍機構運動引起槍口跳動的仿真模型
3.2 導氣壓力作用下槍口偏移量仿真分析
膛壓存在的跳差導致導氣室壓力也存在跳差,經布拉文公式計算,導氣室壓力峰值為66 MPa,跳差為±8 MPa,通過仿真分析,導氣室壓力作用下槍口位移量為1.54 mm,跳差為±0.4 mm,如圖5所示,圖中,s為槍口縱向位移,位移曲線如圖6所示。

圖5 導氣室壓力作用下槍口偏移量仿真
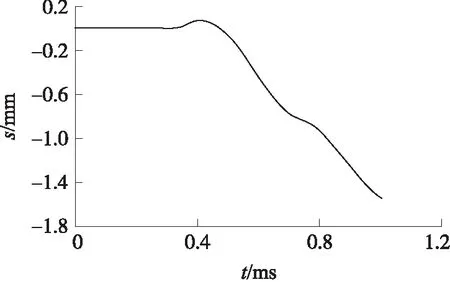
圖6 導氣室壓力作用下槍口偏移量曲線
3.3 彈丸擠進作用下槍口偏移量仿真分析
在彈丸與槍管實際裝配位置的彈丸尾部施加膛壓曲線,彈丸槍管全部劃分成六面體網格,如圖7所示。仿真分析彈丸擠進槍管全過程中彈丸和槍口的運動規律,槍口最大位移量為0.001 mm,雖然變化明顯,但是由于數量級太小,轉換到槍管射角變化,基本為0。實際上彈丸擠進槍管的過程中,槍管受力是軸對稱的,沒有使槍管徑向運動的力。
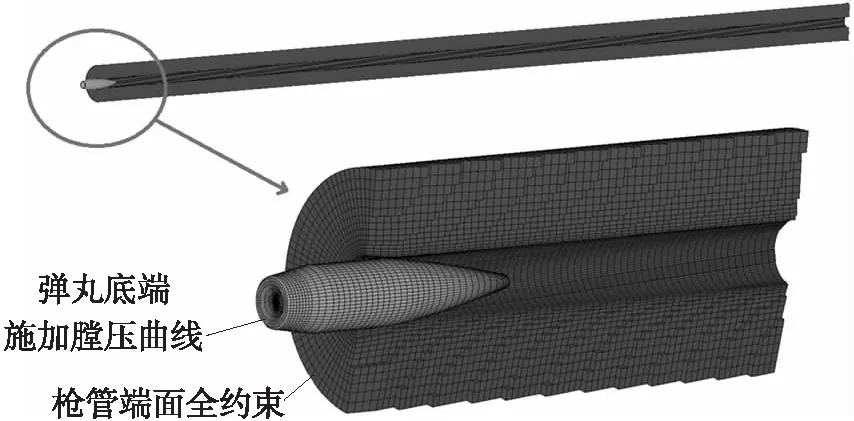
圖7 彈丸擠進槍管仿真模型
3.4 槍口縱向跳角
縱向跳角θ可由圖8計算得出,彈尖處的偏差可近似等于槍口位移量與全槍機構動作引起的槍口跳動量之和,槍口位移量為自動機運動及導氣室壓力作用2個仿真位移量之和,則θ=arctan(1.63/120)=0.78°,跳差為±0.2°。
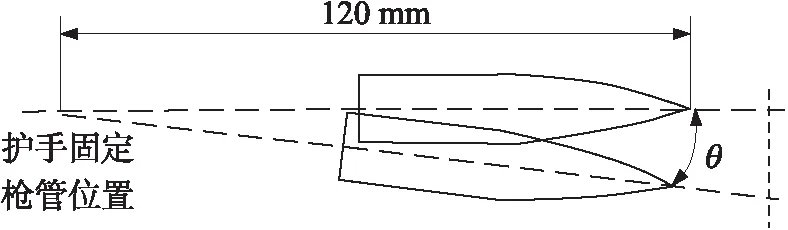
圖8 槍口縱向跳角
4 立靶散布仿真分析模型的建立
立靶散布偏差通常包括縱向偏差和橫向偏差。本文建立在初速、射角影響下的射彈立靶散布統計模型,分析槍彈外彈道散布特性。
確定影響射彈立靶散布的隨機因素,這些因素包括:初速v0、縱向跳角θz、橫向跳角θh、彈形系數i。設隨機因素服從正態分布,彈丸初速均值及標準差來自隨機內彈道計算結果,跳角均值及標準差來自仿真結果,彈形系數均值及標準差來自設計要求及經驗,將這些因素隨機生成20組的組合,作為隨機外彈道仿真的輸入。外彈道隨機變量見表2。

表2 外彈道隨機變量
本文重點研究槍械因素對射擊精度的影響,采用質點外彈道方程,通過循環調用質點外彈道計算程序進行20發隨機外彈道仿真計算,求出4種隨機因素下的20發落點坐標并保存,生成立靶散布圖,并求出平均彈著點R50,R100。3組100 m處立靶散布如圖9所示。
質點外彈道方程采用四階龍格庫塔方法解算,并用C++Builder軟件開發建立解算程序。
考慮氣溫、氣壓非標準的影響,不考慮地球曲率及科氏加速度的影響,質點彈道方程為
(3)
式中:c為彈道系數,H(y)為空氣密度函數,G(v,cs)為阻力函數。
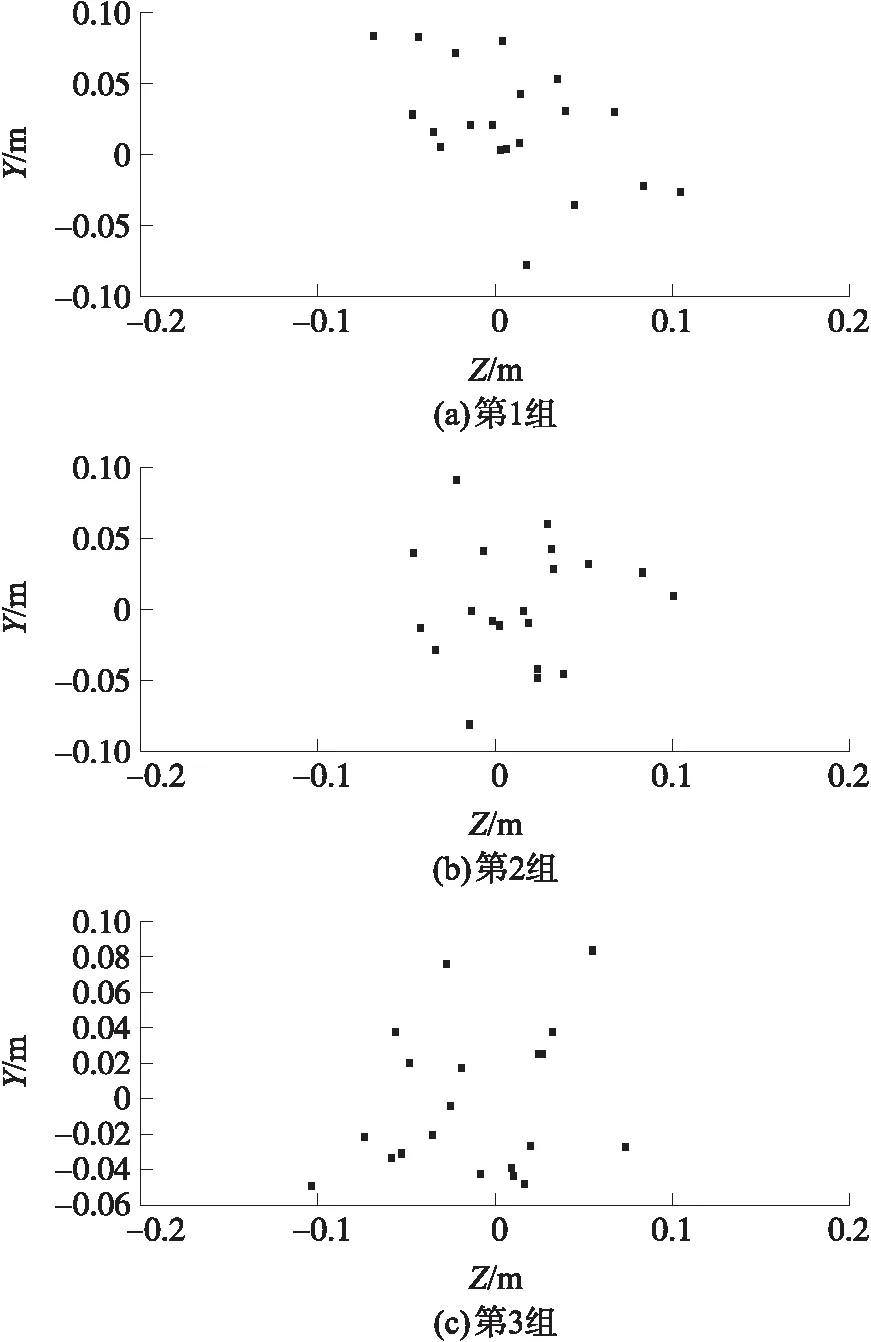
圖9 立靶散布圖(X=100 m)
5 試驗驗證
試驗以某自動步槍為研究對象,將槍托和護手夾持固定,如圖10所示,射擊距離100 m,目標為胸環靶。在槍口附近進行高速攝影,見圖11,拍攝彈丸出槍口瞬間縱向跳動情況,獲取槍口縱向位移s,如表3所示。

圖10 槍械射擊試驗圖

圖11 彈丸出槍口瞬間
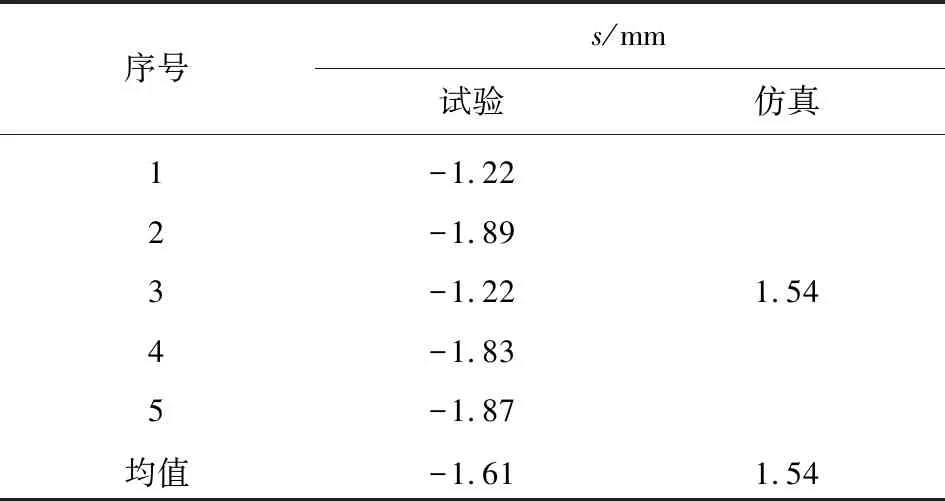
序號s/mm試驗仿真12345-1.22-1.89-1.22-1.83-1.871.54均值-1.611.54
分別進行3組射擊,每組20發,獲取胸環靶射擊結果,如圖12所示,計算得出R50,R100,與仿真結果對比分析,如表4所示。計算可得,仿真結果:σR50=0.29 cm,σR100=2.55 cm;試驗結果:σR50=0.45 cm,σR100=4.42 cm;仿真與試驗均值的相對誤差:rR50=2%,rR100=13.9%。

圖12 胸環靶射擊結果
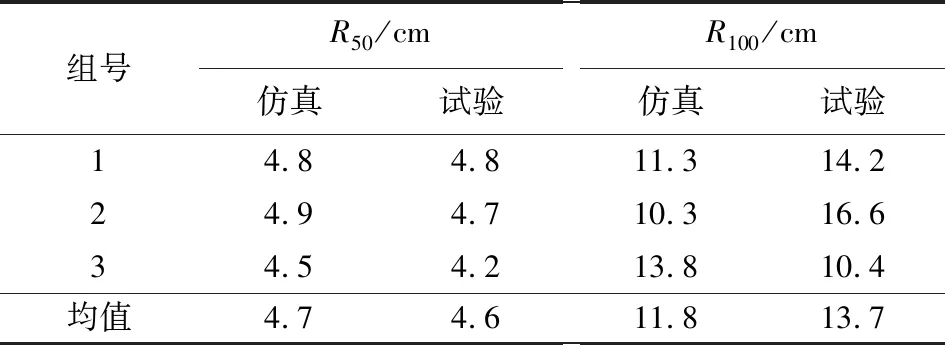
組號R50/cm仿真試驗R100/cm仿真試驗14.84.811.314.224.94.710.316.634.54.213.810.4均值4.74.611.813.7
6 結論
本文基于多體動力學仿真、結構力學仿真、隨機內、外彈道方程,建立了導氣式槍械射擊精度仿真分析模型,初步預測了100 m處的R50,R100,并進行試驗驗證,得到如下結論:
①經對比分析,該槍械槍口偏移量仿真與試驗相對誤差、R50均值相對誤差、R100均值相對誤差均小于15%,說明該技術可用于新型槍械研制中的精度分析。
②本文聚焦于步槍本身對單發射擊精度的影響,尚未充分考慮槍彈因素,如槍彈攻角變化以及后效期膛口流場的影響。本文方法可以分析槍械零部件(如上、下機匣)的公差配合對射擊精度的影響,具有一定的工程應用價值。

