一種縱彎復合單驅動足超聲波電動機的設計

張斯陽

(湖北大學知行學院， 武漢 430011)

0 引 言

超聲波電動機是近幾十年成長的非典型特種微電機，它既沒有傳統電動機的磁極，也沒有電磁感應的過程，超聲波電動機主要運用的是壓電材料的逆壓電效應，讓輸入的電能轉化為輸出所需的機械能[1]、輸出功率、驅動負載[1-2]。

1 縱彎復合超聲波電動機理論分析

1.1 結構設計

本文研究了一種新型的縱彎復合單驅動足超聲波電動機，該電機的結構如圖1所示。該超聲波電動機由后端蓋、法蘭螺栓、法蘭盤、變幅桿、壓電振子、電極、驅動足以及摩擦片組成。法蘭螺栓連接后端蓋與壓電振子以及變幅桿，法蘭盤兩側有兩個錐孔，是兩個夾持點，用于固定電機。兩個變幅桿的小端與驅動足相連接，驅動足輸出位移，驅動足貼有摩擦片。

圖1 電機結構示意圖

圖2為電機壓電振子位置選擇、極化方向以及電路連接情況。兩對縱振壓電振子在d33模式下工作，每對縱振壓電振子中的每片縱振壓電振子的極化方向相反，每片縱振壓電振子的極化方向與關于驅動足相對稱的縱振壓電振子的極化方向相同，每片縱振壓電振子均置于縱振振型的節點處，從而保證一組壓電振子在收縮狀態時，另一組壓電振子處于伸長狀態，實現驅動足的推拉諧振運動[3]。兩對彎振壓電振子在d31模式下工作，每對彎振壓電振子的極化方向相同，每片彎振壓電振子的極化方向與關于驅動足相對稱的彎振壓電振子的極化方向相同，每片彎振壓電振子均置于電機振型的波腹處。

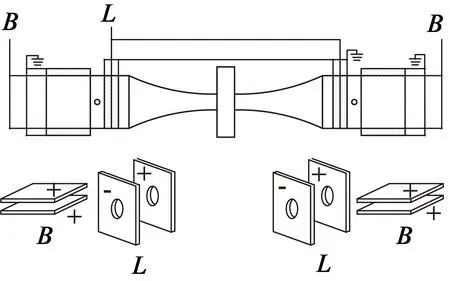
圖2 壓電振子的極化方向布置與接線情況

1.2 工作原理

1.2.1 驅動足的運動軌跡分析

如圖3所示，在驅動足與動子相接觸的一側取面中心O，在壓電振子的激勵下，定子產生縱向振動與彎曲振動的響應，驅動足分別在Y軸和X軸的方向上進行簡諧振動，則點O在Y軸和X軸的方向上的位移y和x分別如下：

(1)

式中：W1為驅動足在Y向上的振動幅值；W2為驅動足在X向上的振動幅值；α為Y向上的振動初始相位；β為X向上的振動初始相位；ω為超聲波電動機的諧振頻率。

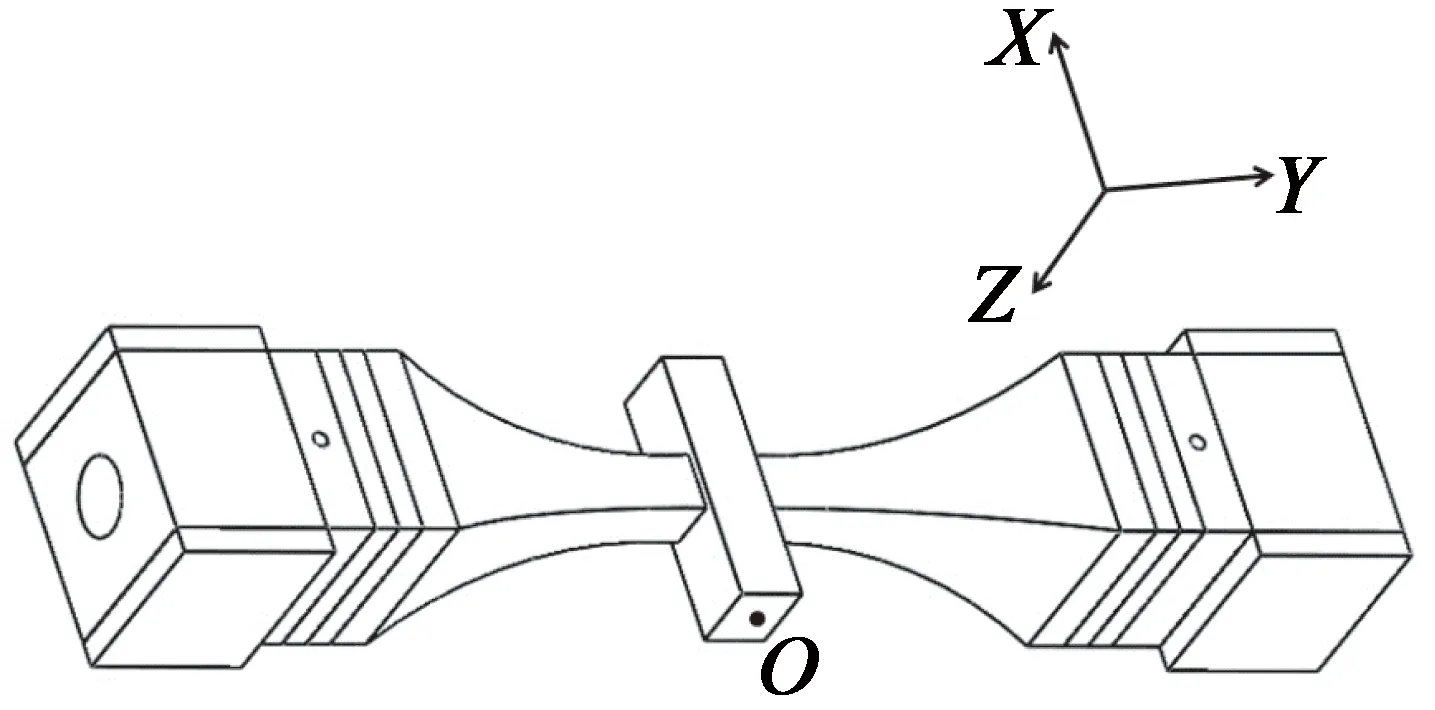
圖3 驅動面的中心

對式(1)進行三角變換，可得：

(2)

從式(2)可以看出，中心O在XOY平面內的運動軌跡為橢圓，且橢圓的中心即為O的靜止點。電機所受的兩相激勵電壓的相位差β-α決定了軌跡橢圓主軸的方向。分別令相位差β-α如下：

(3)

可得中心O的運動軌跡如圖4所示。

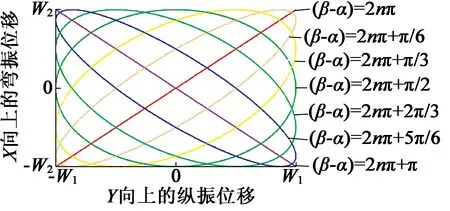
圖4 不同相位差下中心O的運動軌跡

圖4表明，通過具有一定相位差的縱振和彎振組合，驅動足可以實現以橢圓軌跡運動的激勵，縱振和彎振的振幅與相位差決定了橢圓軌跡的主軸長度和主軸方向。

當β-α=π/2時，式(2)簡化：

(4)

式(4)表明，對于彎振超聲波電動機，當兩相激勵電壓之間的相位角為π/2時，其驅動面中心O點在XOY平面內的運動軌跡為主軸的方向分別為OY和OX方向的橢圓，且W1和W2分別為橢圓主軸的長度，我們可以通過調整兩相激勵交變電壓的幅值來調整橢圓軌跡主軸長度。

1.2.2 電機的運動機理分析

給縱振壓電振子加載sin(2πft)(f為縱彎簡并后的諧振頻率)的交流電壓，給彎振壓電振子加載cos(2πft)的交流電壓。縱振壓電振子在d33的工作模式下激勵電機的縱振模態，彎振壓電振子在d31的工作模式下激勵電機的彎振模態，縱振模態和彎曲模態相疊加，驅動足的運動軌跡呈橢圓。若將加載的兩相交流電壓的相位差改為-π/2，電機可以實現反向驅動。電機在一個周期內的振型變化如圖5所示。

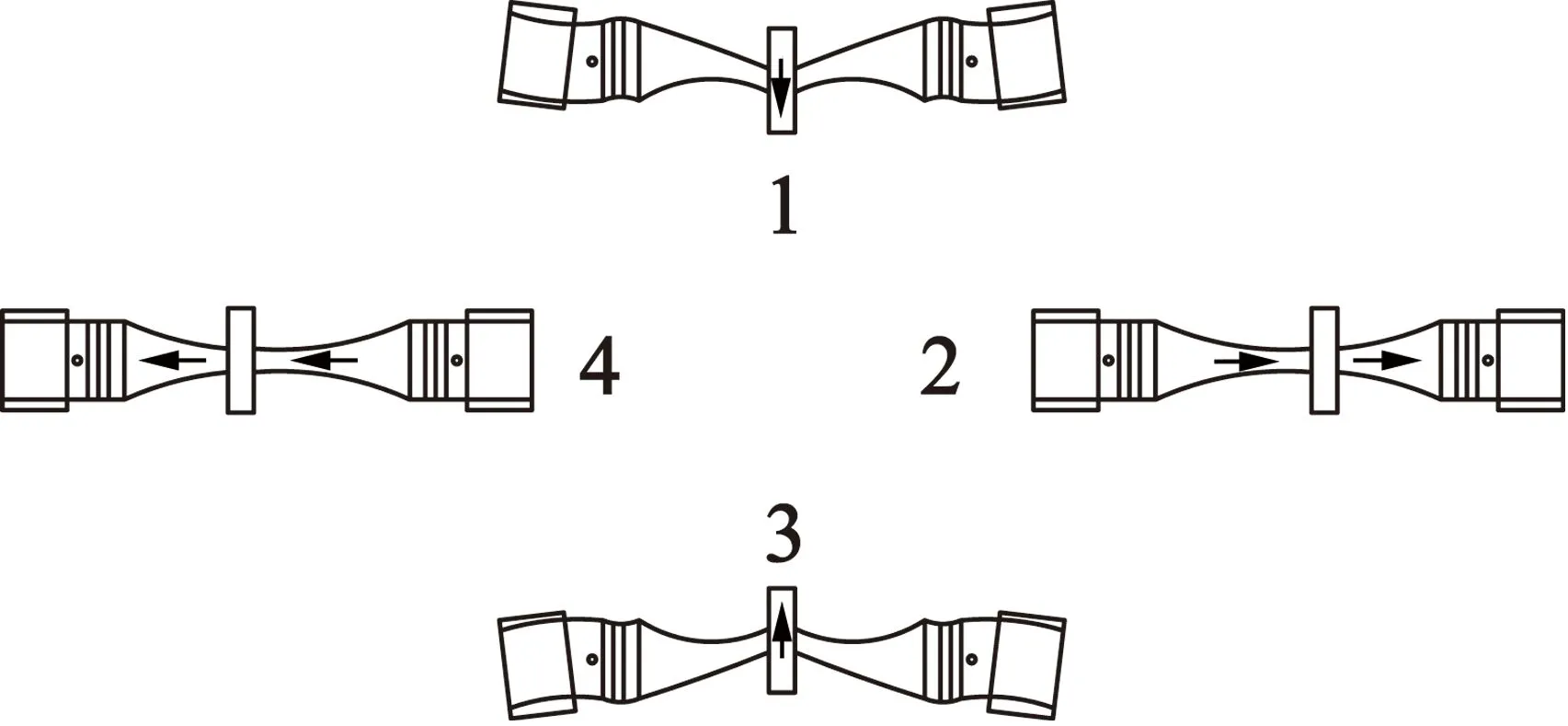
圖5 電機在一個周期內的振型變化

2 縱彎復合超聲波電動機結構設計

2.1 模型的建立

本文設計的縱彎復合單驅動足超聲波電動機選用的壓電材料為PZT-5H，變幅桿、驅動足以及法蘭盤均選擇硬鋁合金，后端蓋的材料選擇45#鋼。圖6為在ANSYS中建立的縱彎復合單驅動足超聲波電動機的有限元模型。

圖6 電機的有限元模型

2.2 結構參數靈敏度分析

縱彎復合單驅動足超聲波電動機的結構參數對電機的縱振、彎振頻率均有影響，但不同的參數對頻率的影響效果不同。本文采用有限元進行分析，通過數據和圖形的對比，找出不同參數對縱振以及彎振諧振頻率的靈敏度。圖7為標注了結構尺寸的電機[3-6]。

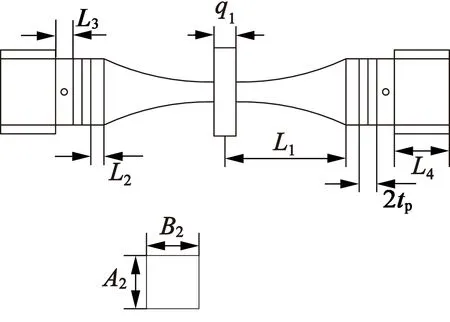
圖7 電機的尺寸標注

從圖7可以看出，電機的主要結構參數有：L1為變幅桿的長度，L2為變幅桿基座長度，tp為壓電振子的厚度，L3為法蘭盤厚度，L4為后端蓋長度；壓電振子、法蘭盤和后端的橫截面尺寸一致，寬度為A2，厚度為B2，驅動足的寬度為q1，變幅桿寬度變化系數為η，變幅桿厚度變化系數為ξ。初始結構參數如表1所示。

表1 初始結構參數/mm

將表1中的初始結構參數輸入ANSYS，建立電機有限元模型，將電極面上的節點耦合，模型加載電壓后對電極進行短路處理。對電機進行模態分析，得到電機的一階縱振模態和五階彎振模態分別如圖8和圖9所示。

圖8 一階縱振模態

圖9 五階彎振模態

經過對有限元模型的計算，在初始結構參數條件下，一階縱振頻率為31 242Hz，五階彎振頻率為36 395Hz，頻率差值為5 153Hz。可見，在初始參數條件下，縱振彎振的頻率差值較大，需要對模型的結構參數進行優化，使頻率差值盡量接近。

通過有限元分析，得出各參數對諧振頻率的影響，如圖10所示。

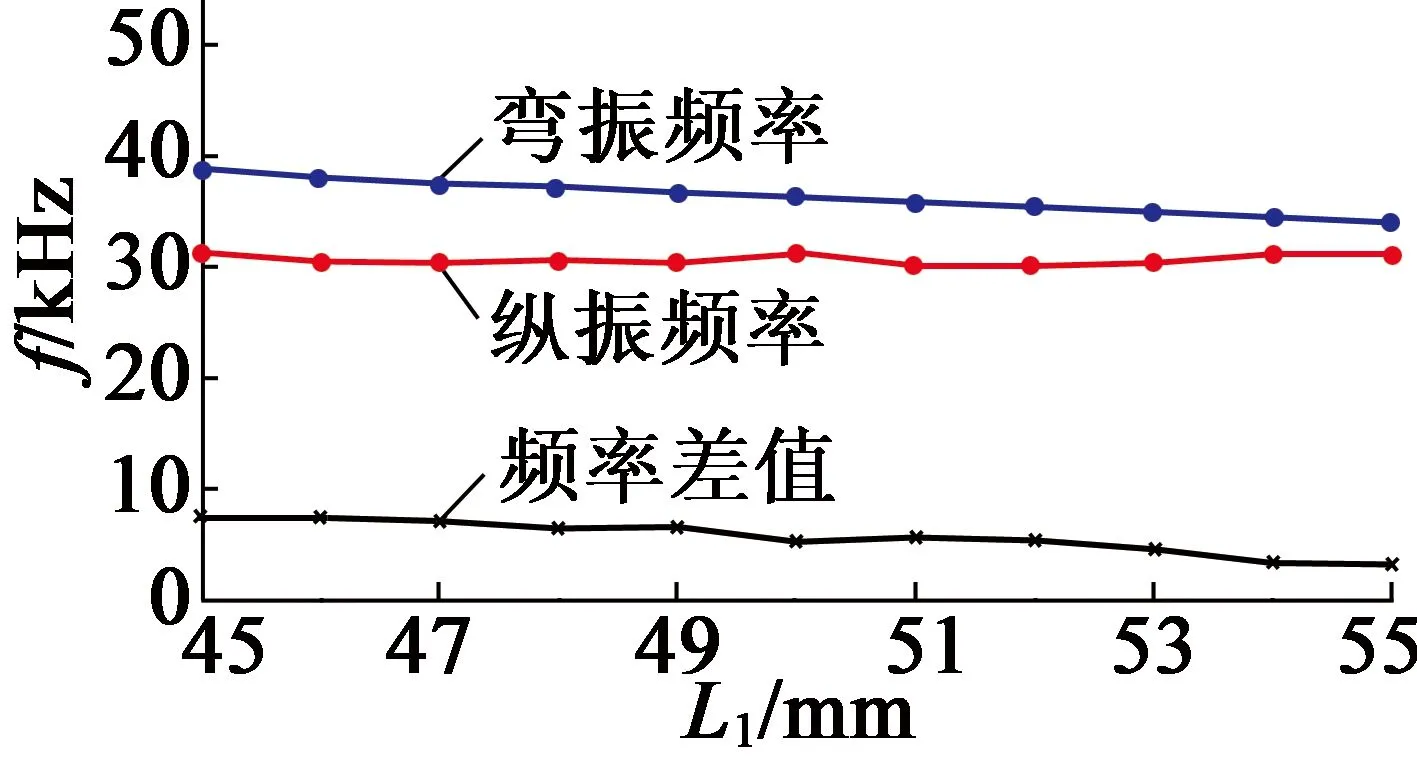
(a) L1

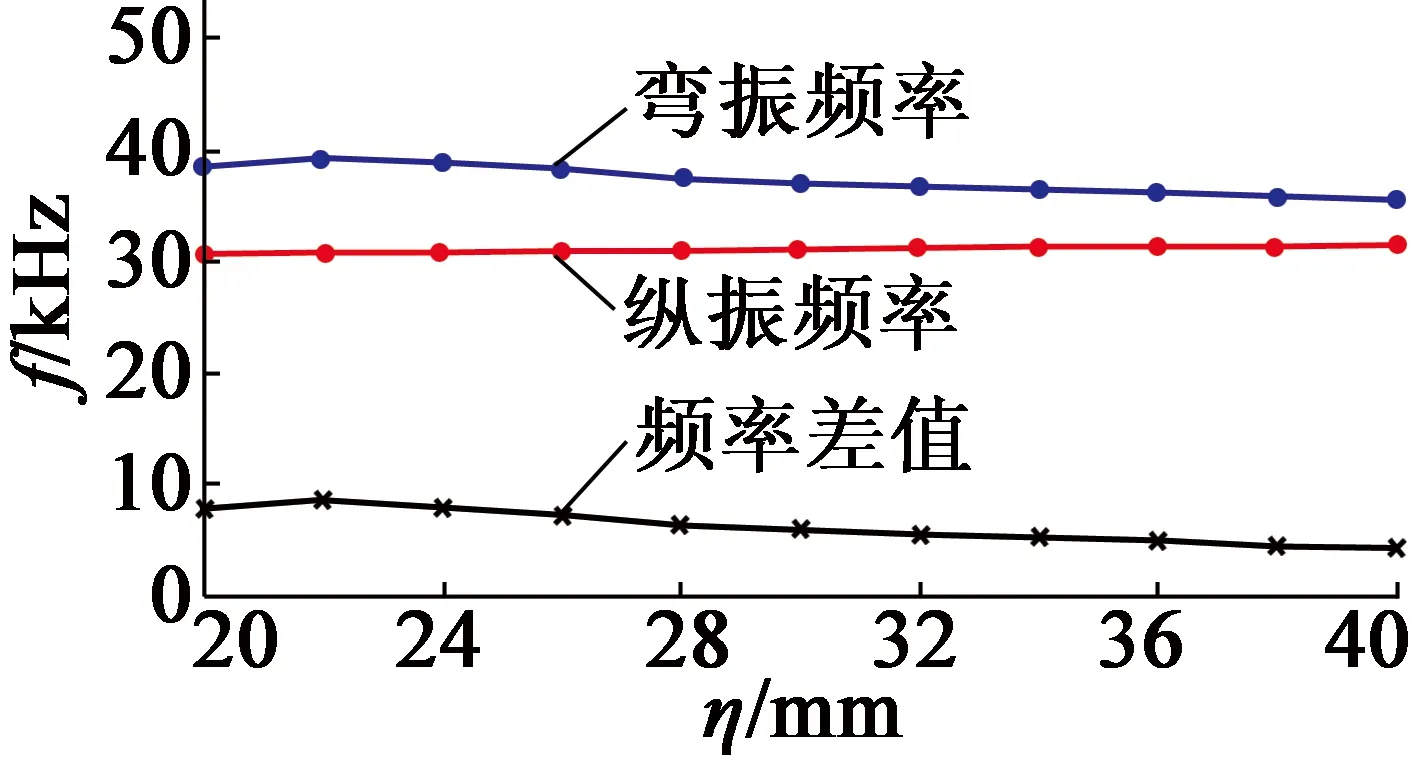
(b) η

(c) ξ

(d) L2

(e) tp

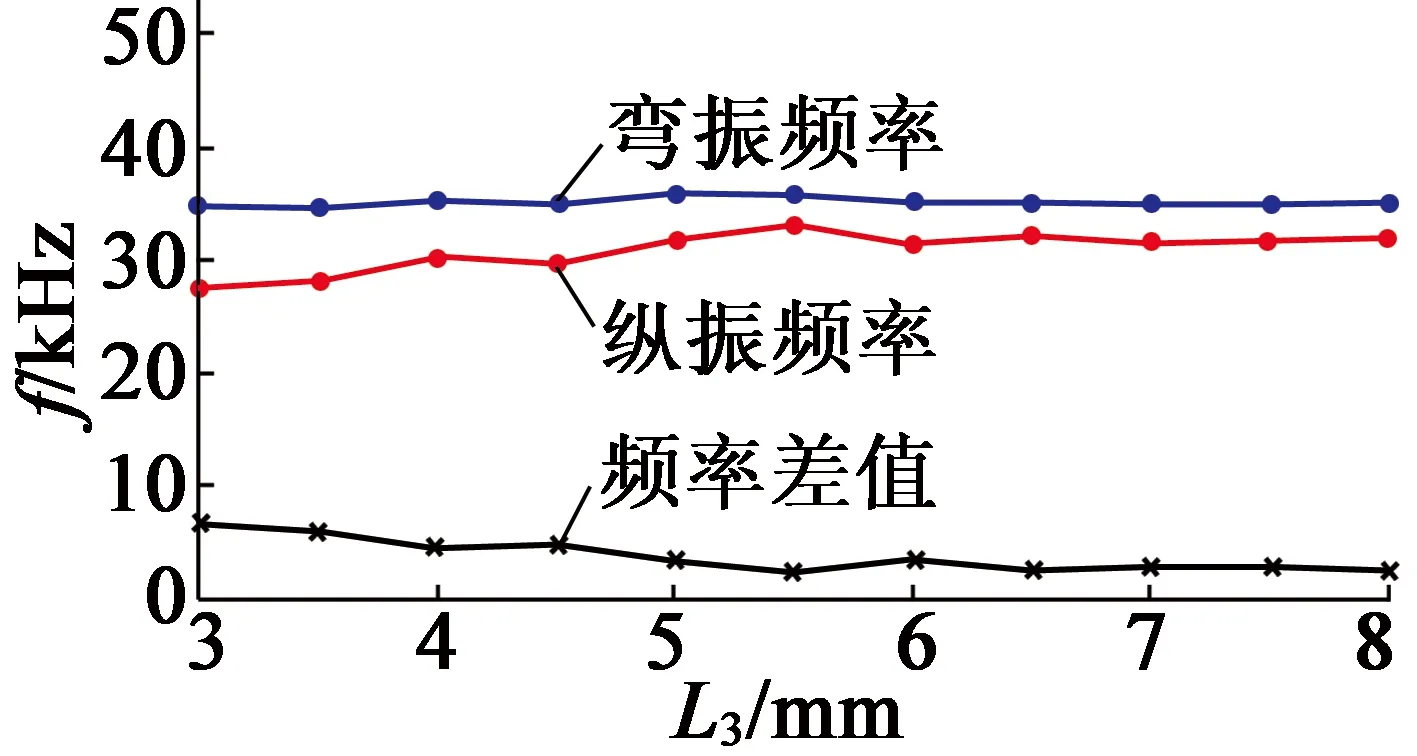
(f) L3

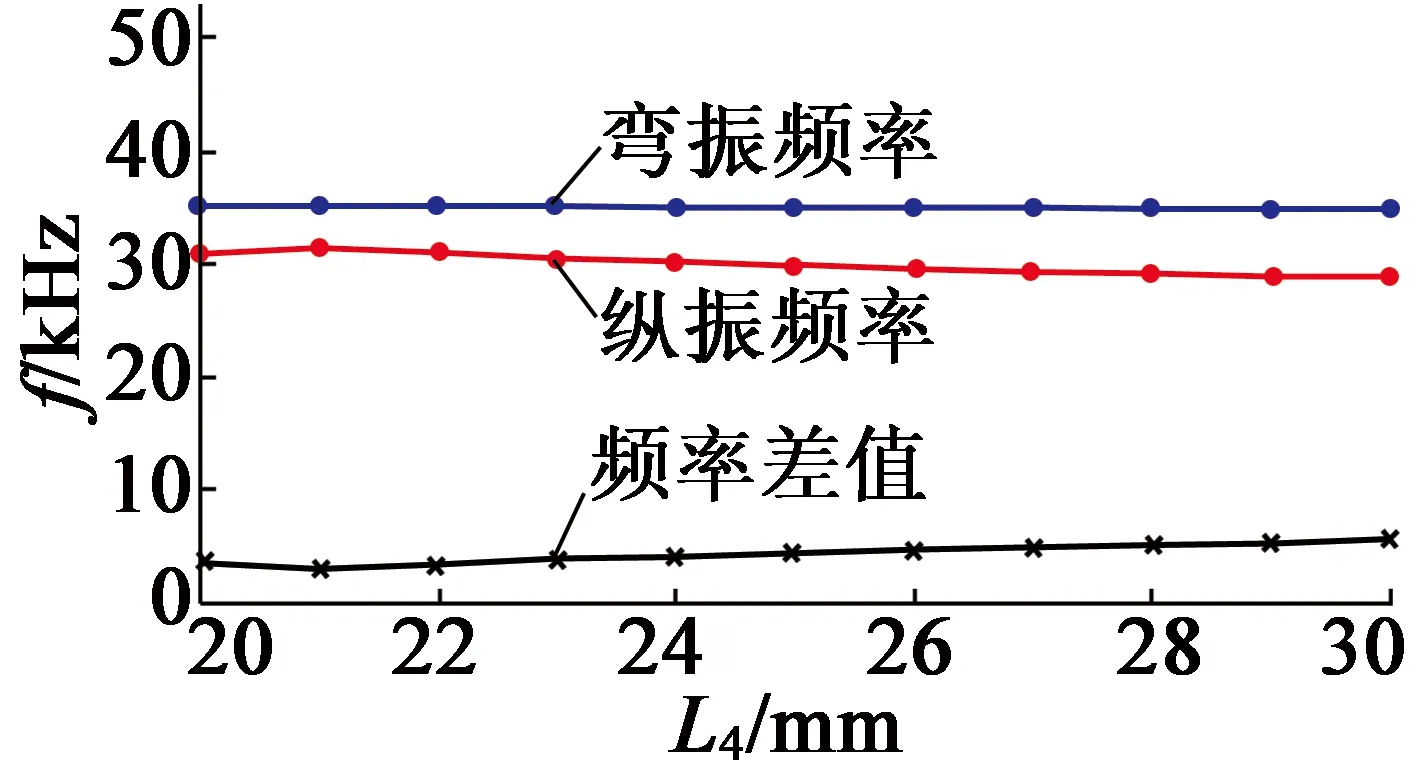
(g) L4

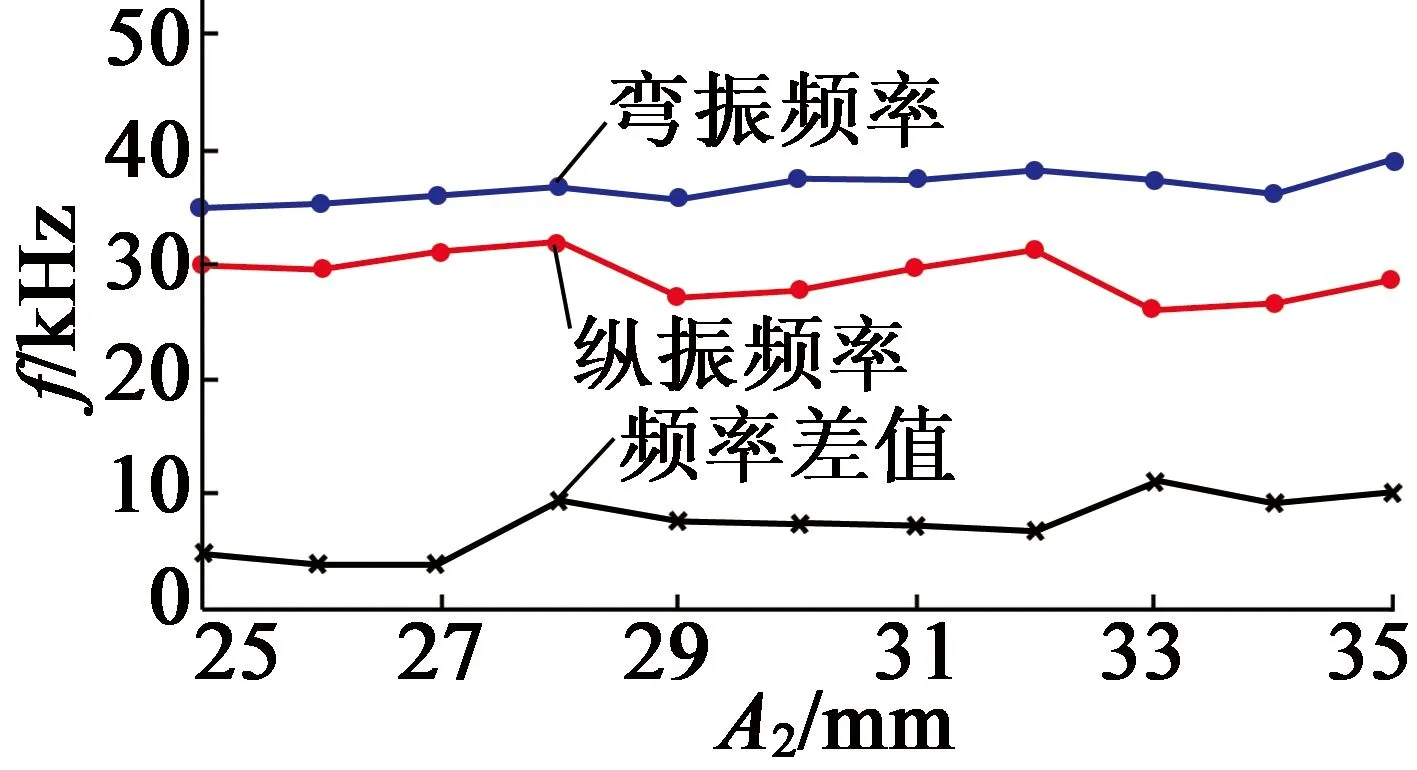
(h) A2

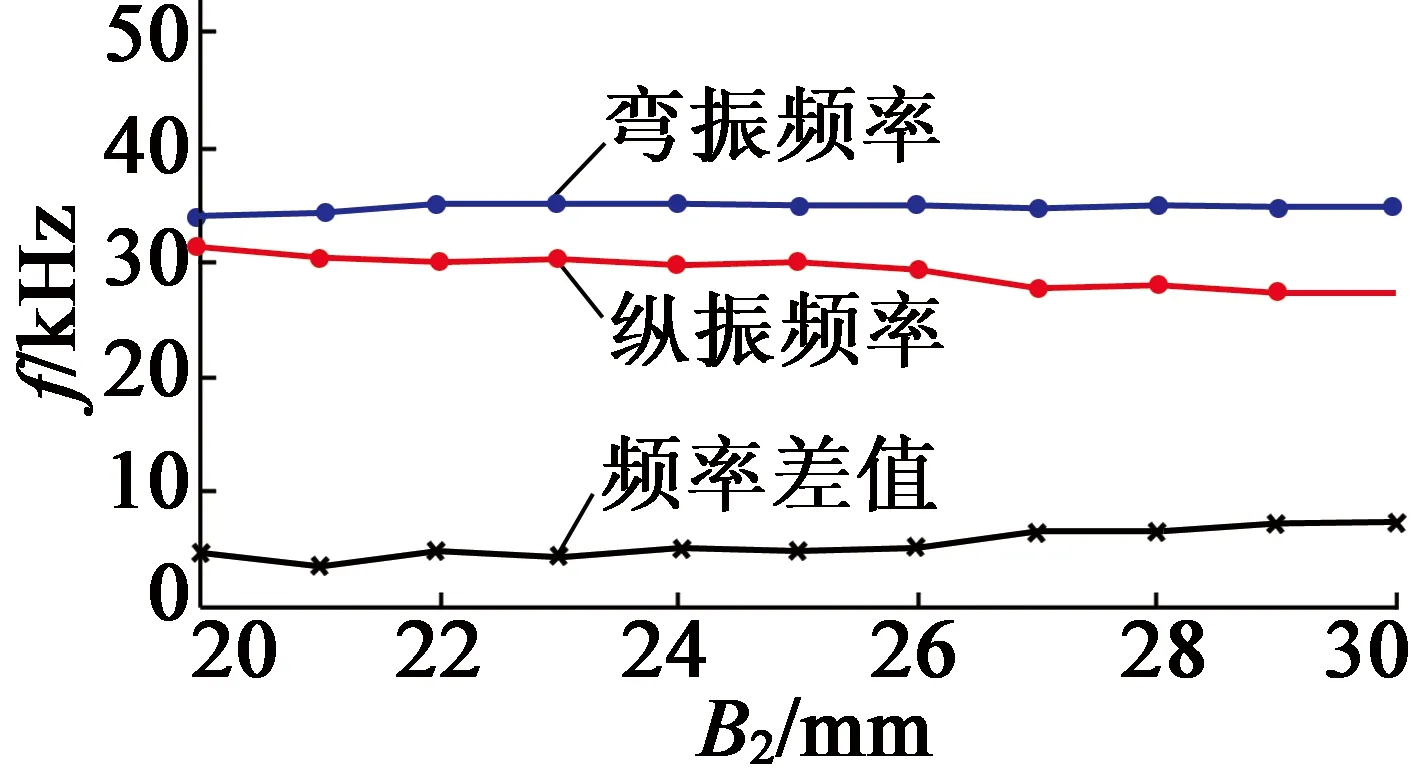
(i) B2

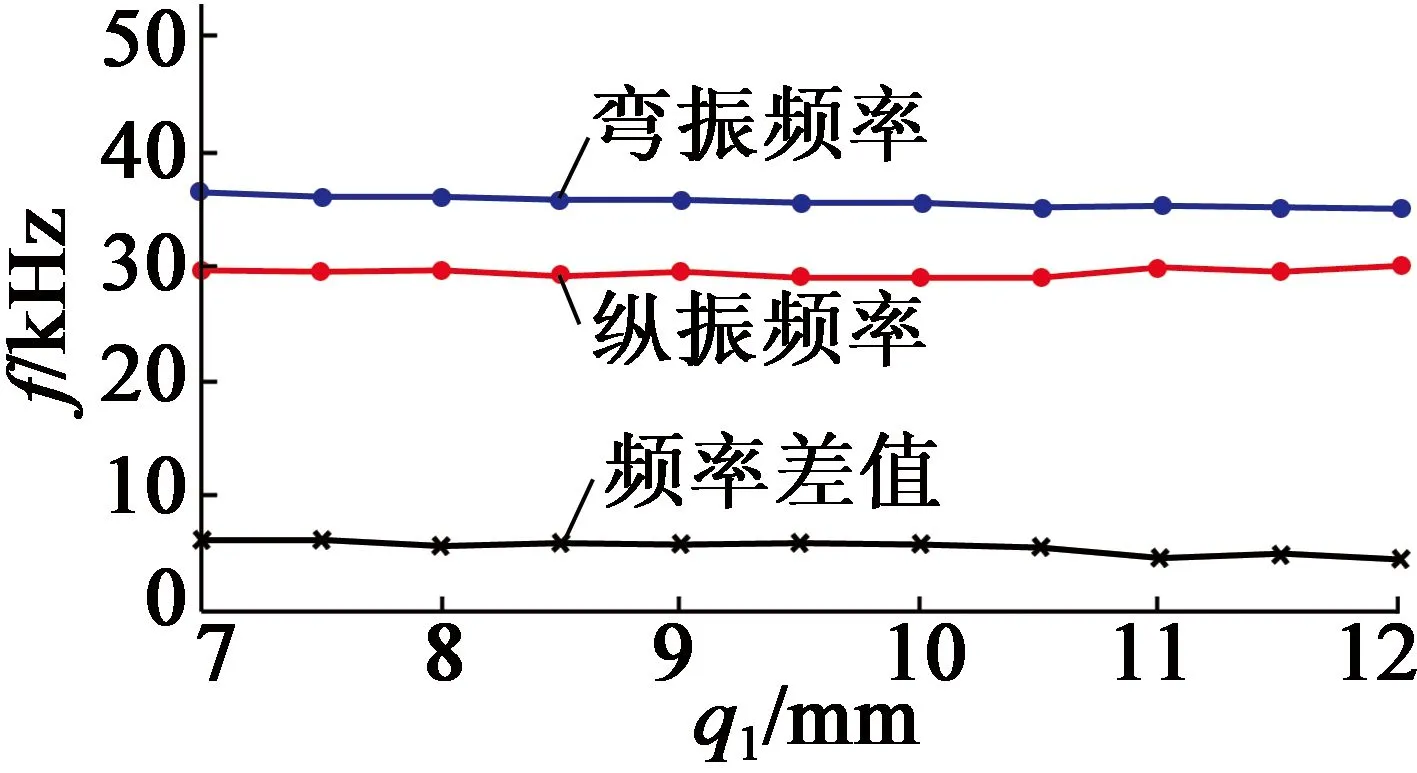
(j) q1

圖10各參數對諧振頻率的影響

2.3 縱彎模態簡并

根據上述分析，了解到各個結構參數對縱彎超聲波電動機各階諧振頻率的影響。首先調整10個結構參數，使一階縱振頻率與五階彎振頻率盡量接近；再微調變幅桿的各個系數，找到能使縱振頻率和彎振頻率最為接近的系數；并保證其諧振頻率在超聲波頻率以上，以避免超聲波電動機產生噪聲。其中，法蘭盤厚度L3為5.5mm和6.5mm時，一階縱振模態出現縱振和扭振模態，不可取。優化后的結構尺寸參數如表2所示。

表2 優化后結構參數/mm

建立優化參數后的縱彎超聲波電動機有限元模型，在ANSYS中實現模態分析，可得其一階縱振頻率為26 435 Hz，五階彎振頻率為26 507 Hz，頻率差值變為73 Hz。縱振模態和彎振模態如圖11所示，基本實現了縱彎模態簡并。特別強調的是，在優化參數的過程中，縱振壓電振子位于縱振的節點位置，彎振壓電振子位于彎振的波峰/波谷處，使縱向振動和彎曲振動的激勵充分利用。法蘭盤位于彎振的節點處，可盡量約束對激勵的影響。

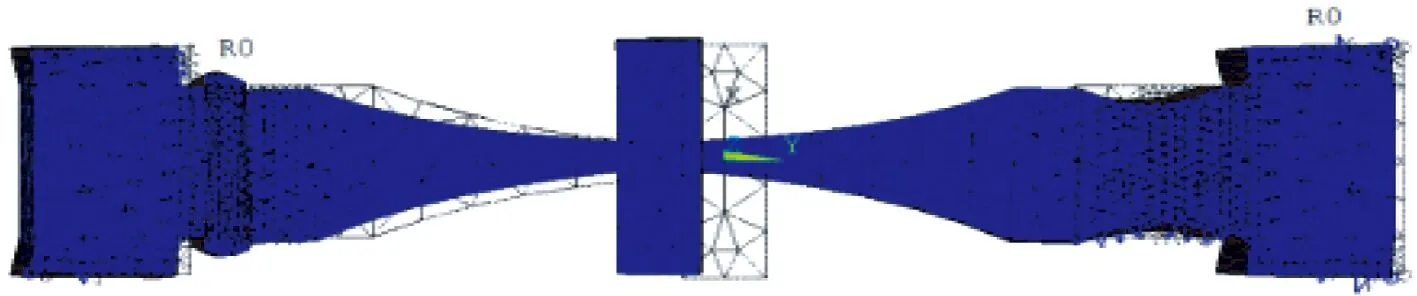
(a) 一階縱振模態

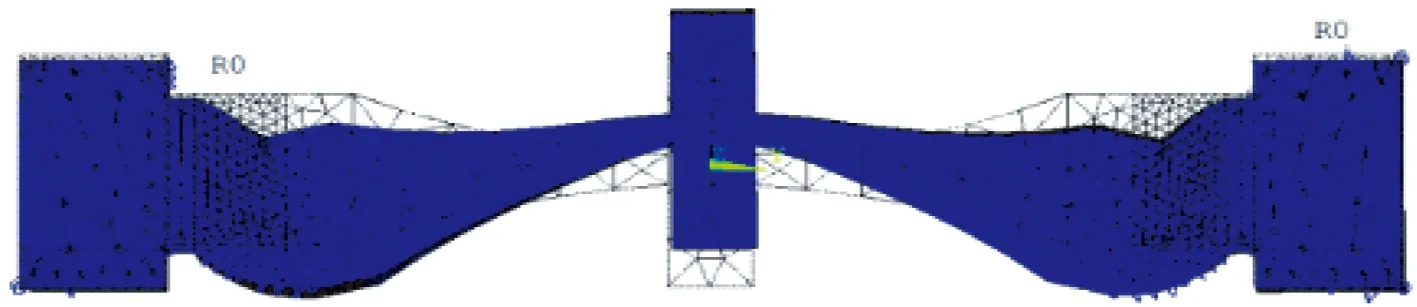
(b) 五階彎振模態

3 結 語

本文設計了一款新型的將壓電材料d31和d33相結合的縱彎復合單驅動足超聲波電動機，確定了其壓電振子的分布以及極化方向，設計了超聲波電動機的電路連接方式。對縱彎復合單驅動足超聲波電動機的10個結構參數進行了靈敏度分析，得到不同參數對電機的縱振模態、彎振模態以及頻率差值的影響，并進行了縱彎簡并，得到了理想的結構參數。