基于割線法的超聲波電動機迭代學習轉速控制

周 穎，宋 璐，史敬灼

(河南科技大學 電氣工程學院，洛陽 471023)

0 引 言

超聲波電動機固有的非線性運行特性，要求其控制策略具有應對這種非線性的能力，以得到良好的控制性能[1]。作為一種針對非線性被控對象的控制策略，迭代學習控制策略具有算法相對簡單的優點。它采用基于記憶的學習控制方法，利用過去的控制信息，通過自身學習不斷調整控制器的輸出，逐步改善控制效果。

文獻[2]給出牛頓學習律和正割學習律兩種非線性迭代學習控制策略。文獻[3]將非線性正割迭代學習律用于超聲波電動機的轉速控制，針對電機的時變特征進行改進，消除穩態誤差。文獻[4-5]分別將雙層最優迭代學習和非線性正割迭代學習控制策略用于超聲波電動機位置控制，并采用蘑菇繁殖優化算法對控制器參數進行優化。

本文針對超聲波電動機非線性運行特性，將數值分析中的割線法用于迭代學習控制，給出了簡單的超聲波電動機轉速非線性迭代學習控制策略。實驗表明，電機轉速控制性能在迭代學習過程中逐漸趨于期望，控制效果良好。

1 超聲波電動機迭代學習轉速控制策略

文獻[2]借用數值分析中用來求解非線性方程的牛頓法，給出了一種簡單的非線性學習控制律，稱之為牛頓學習律。其控制量表達式：

(1)

式中：uk+1(t)，uk(t)分別為系統第k+1，k次運行過程中t時刻的控制器輸出控制量，所用控制量為電機驅動電壓的頻率；ek(t)為系統第k次運行過程中t時刻的轉速誤差；KP為學習增益；g為控制系統的輸出函數。

包括迭代學習控制在內的各種控制策略，都是通過設計控制律來尋求使得系統誤差e=0或是趨于0的控制量u。而達到e=0的過程是否穩健、是否快速，是控制系統動態性能的主要表征，也是用來評價控制策略優劣的主要衡量標準。式(1)等號右側采用前次而不是當前運行過程中的控制量、誤差數值進行計算，從而使這一借用來的牛頓學習律又具有了迭代學習的特征，成為一種非線性迭代學習控制策略。

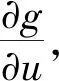
(2)

(3)

式(3)的割線學習律，采用前次控制過程的控制量、轉速誤差數值計算當前控制量，屬于傳統的開環迭代學習控制策略。另外，超聲波電動機轉速隨著驅動頻率下降而升高，式(3)中的學習增益KP應為負值。

2 割線迭代學習控制策略的實用化改進

采用式(3)作為超聲波電動機轉速迭代學習控制器，進行迭代學習轉速控制實驗研究。實驗用電機為Shinsei USR60兩相行波型超聲波電動機，驅動主電路采用H橋結構。與電機同軸剛性連接的光電編碼器，在線測量電機轉速并反饋到控制器輸入端，控制器輸出量為電機驅動頻率。

在迭代學習控制實驗過程中，第1次階躍響應過程采用比例系數為-1、積分系數為-2的PI轉速控制器；隨后，取學習增益KP為-0.5，連續進行5次割線迭代學習控制實驗，共測得6次階躍響應過程。圖1給出了階躍給定值為30 r/min情況下的實驗結果。可以看到，第2，3，4次階躍響應曲線沒有超調，但第5，6次階躍響應出現超調。另一方面，圖1的迭代學習響應曲線也出現了一些不理想的狀況，下面一一分析并給出解決辦法。

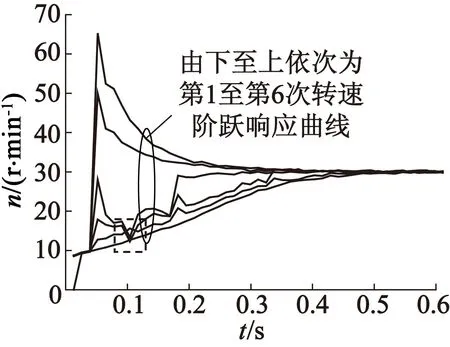
圖1 轉速階躍響應曲線(KP=-0.5，空載)

2.1 轉速凹陷

圖1中第2，3，4次轉速階躍響應曲線不平滑，出現一些凹陷與波動。為分析其原因，將圖1中虛線矩形區域放大如圖2所示。圖2給出了局部的第2，3，4次轉速階躍響應曲線，并標出了實測數據點。按照式(3)及實驗數據，計算這3次階躍響應控制過程中的控制量相關數據，如表1所示。表1中給出的數據是DSP程序中使用的16位定點數值。為保持控制過程的原貌以便分析、理解，本文未將其變化為以kHz為單位的頻率值。

圖2 轉速階躍響應曲線(局部)

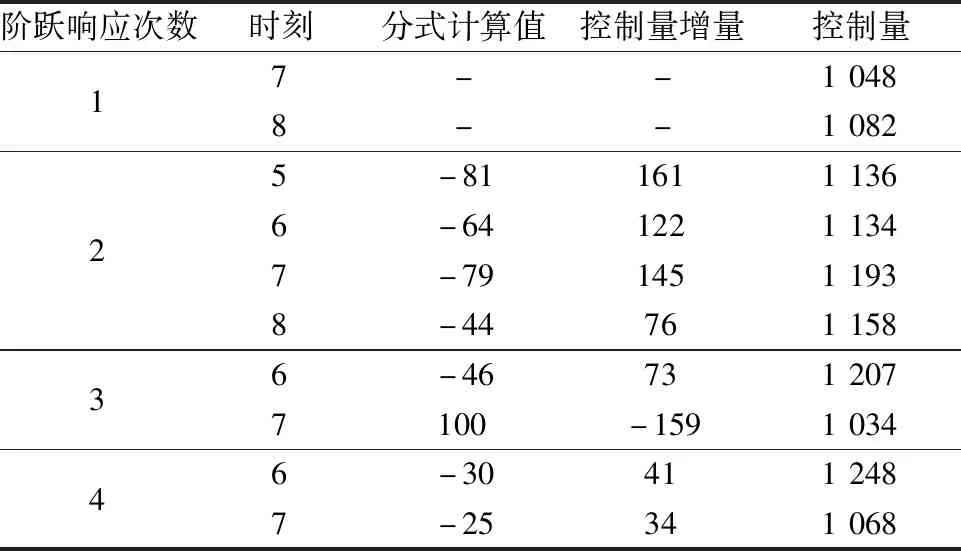
階躍響應次數時刻分式計算值控制量增量控制量17--10488--108225-8116111366-6412211347-7914511938-4476115836-467312077100-159103446-304112487-25341068

從表1中可知，第2次階躍響應過程中，第8個時刻式(3)右側第二項的計算值，即控制量增量為76，明顯小于第7時刻控制量增量值145，在疊加前次階躍響應控制量之后，所得控制量值1 158依然小于第7時刻控制量值1 193。由第7時刻到第8時刻，控制量值的減小，導致了圖2中第2次箭頭所指的轉速凹陷。圖1中，第3，4次轉速階躍響應起始階段的轉速降落，也是同樣原因引起的。由上述分析可知，當轉速處于上升過程中，控制過程中相鄰時刻控制量增量數值大小不同，可能導致當前時刻控制量小于前一時刻的控制量，使得轉速不升反降。為避免轉速凹陷，應在上升階段保持控制量的持續增加。為此，在控制策略中，若當前控制量會導致轉速誤差增大，則改用式(4)計算控制量：

(4)

式中：p為比例系數，用于調節式(4)的控制強度，以保證平穩的整體控制過程。換用式(4)計算當前控制量，因為之前已經完成了式(3)等號右側第二項的計算，所以減小了在線計算量。將式(3)中與分式相乘的ek(i+1)修改為ek+1(i)，以減小當前時刻的電機轉速誤差為目的來確定適當的控制量增量，事實上構成了閉環控制。

2.2 分式計算值符號錯誤導致的轉速下降

考察表1中的第2，3次轉速控制過程數據，第2次5，6時刻的控制量分別為1 136和1 134，第7個時刻式(3)分式中的分子(即控制量增量)為-2，而對應分母即轉速誤差的變化量為-0.02，由此導致分式計算值為100，對應計算出來的控制量增量為-159，使得當前時刻計算的控制量數值大幅度減小，導致了圖1的轉速較大幅度下降。

分析這一現象的原因是轉速測量誤差與噪聲的影響。由于控制過程中控制量變化值很小，對應的轉速變化量也很小，被淹沒在測量誤差和噪聲中，測得的轉速值反而稍增，于是導致了分式計算值的符號錯誤。從本質上來看，牛頓學習律中的微分，割線學習律中的差分，都會放大控制系統中的隨機誤差和噪聲信號，從而影響控制性能。

針對這種情況，在控制策略中，當式(3)分式值符號錯誤時，使用式(5)修正分式計算值，用于控制量的后續計算：

(5)

式中：m為式(3)等號右側分式的計算值，即：

(6)

2.3 電機突停

采用柔化階躍給定進行迭代學習控制實驗中，出現如圖3所示情況，第2次階躍響應的轉速在上升過程中，突降為0。經數據計算分析可知，由于控制量突增，變化量過大，變化過快，超出了實驗用超聲波電動機的承受能力，使得電機突然停止轉動。轉速誤差是轉速給定值與轉速值之差，在柔化階躍給定的情況下，轉速給定值是按照圖3中虛線所示曲線變化的。給定值的變化也會影響轉速誤差值，這是導致上述突停現象的直接原因。

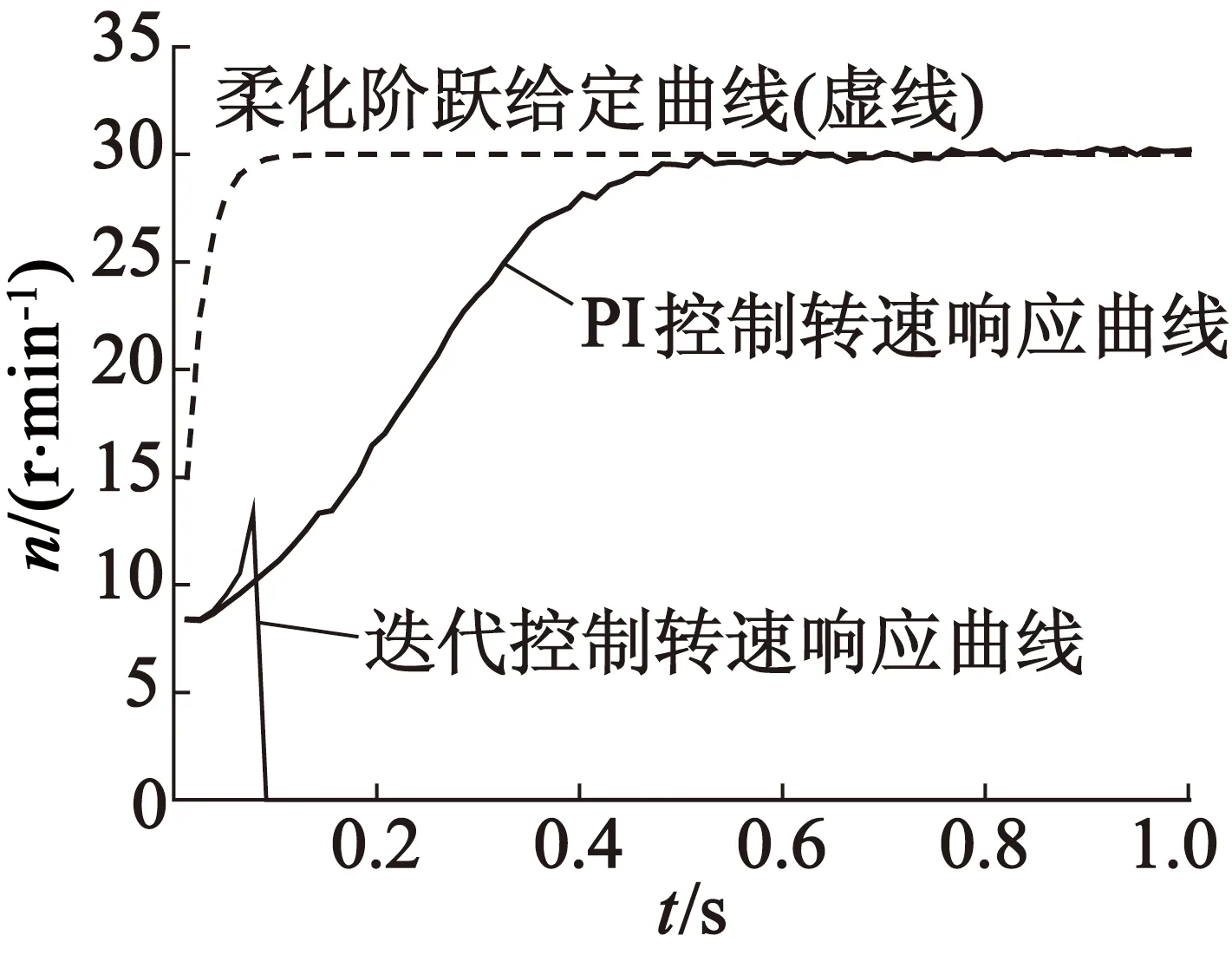
圖3 柔化的轉速階躍響應曲線(KP=-0.5，空載)

考察割線學習律式(3)，其中分式的用意是表述控制量變化導致的轉速誤差變化量，分式計算值再乘以轉速誤差，就得到使當前轉速誤差為0所需的控制量增量。但實際上，對控制量的調節，只會影響電機轉速，而不可能改變外來的給定值。為了更準確地表達了控制量變化的作用效果，將割線學習律式(3)修改：

(7)

3 割線迭代學習控制策略的實驗研究

對非線性割線迭代學習控制策略進行上述三項實用化改進，通過DSP編程實現迭代學習控制律，進行實驗研究，實驗用電機、硬件及實驗過程同前。為便于比較，控制參數設為KP=-0.3，p=1.33，轉速階躍給定值30 r/min，得到階躍給定情況下的實驗結果如圖4所示。從實驗結果來看，前述轉速凹陷、下降、突停等問題都不再出現，轉速上升過程平穩，表明前述改進措施有效。與圖1實驗結果對比，圖4給出的所有轉速階躍響應轉速響應沒有超調，調節時間等性能指標平穩趨好。

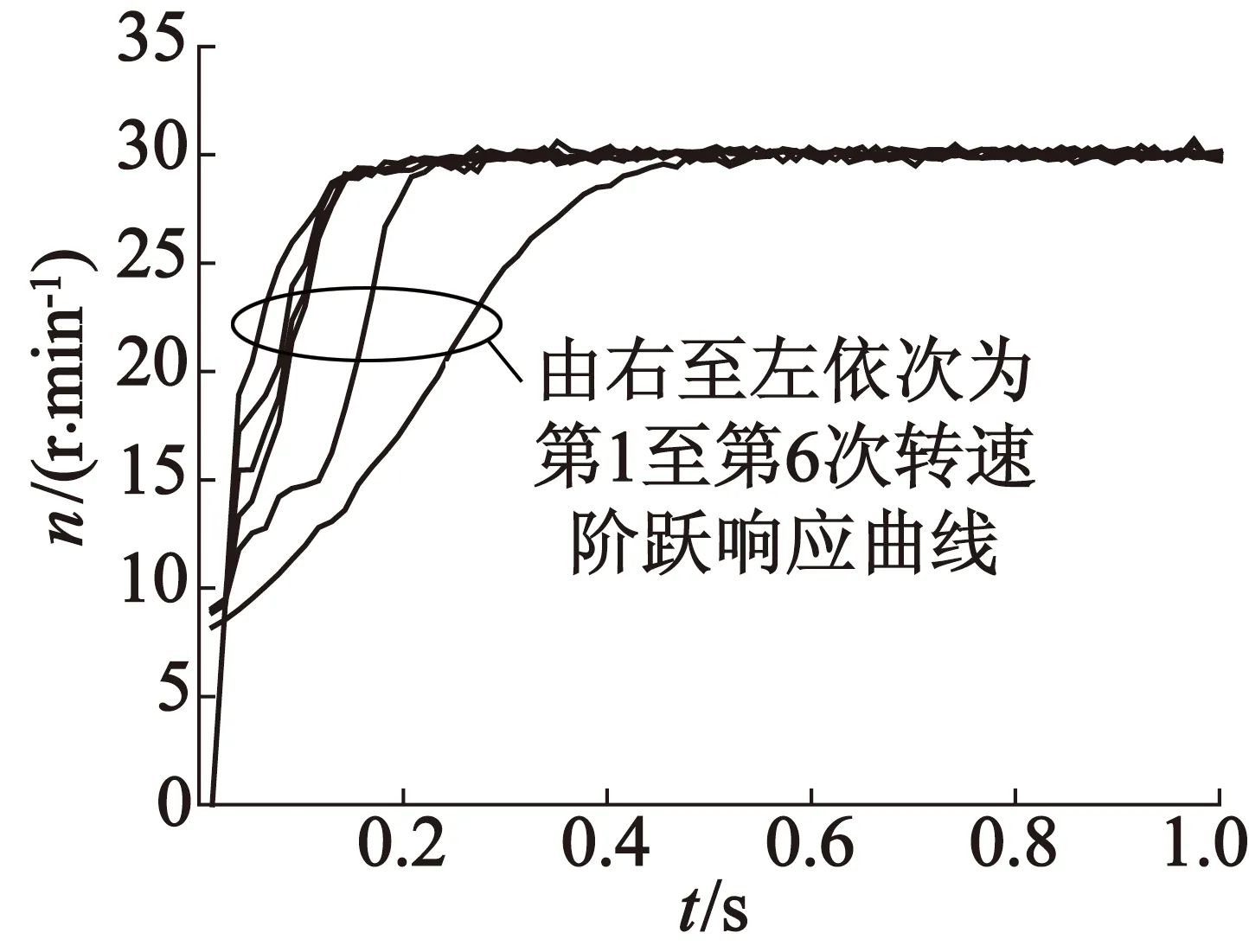
圖4 轉速階躍響應曲線(KP=-0.3，空載)

取階躍給定值為60 r/min，控制參數KP=-0.2，p=2，圖5給出了加載0.2 N·m時的迭代學習控制響應曲線。可以看出，加載后第1次到第6次階躍響應速度變慢，控制性能的改進幅度明顯減小。

但在加載的情況下，所用迭代學習控制策略依然能夠有效地逐步改進控制效果，表明所述割線迭代學習控制策略對負載變化有一定的魯棒性。同時，由于加載，轉速階躍響應曲線更為平滑，穩態轉速誤差大幅度減小。

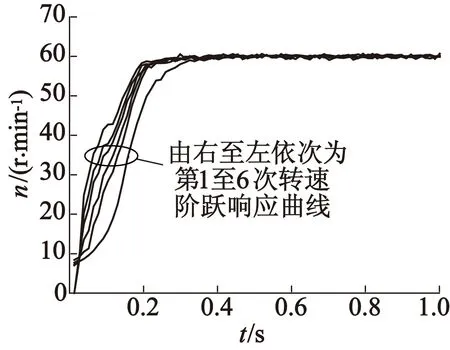
圖5 轉速階躍響應曲線(KP=-0.2，加載0.2 N·m)

4 結 語

本文針對超聲波電動機的非線性及時變特性，在牛頓學習律的基礎上，借用數值分析中的割線法，給出了割線學習律，以解決牛頓學習律中微分項無法準確獲取的問題。將割線學習律用于超聲波電動機非線性迭代學習轉速控制，針對實用中存在的問題，給出3種實用化改進措施。不同工況下的實驗結果表明，割線迭代學習律的控制性能良好。