例說微積分中的經典題的突破方法

■河南省太康縣第一高級中學 董珍珍

在高中階段,由于利用定義法求定積分的過程(四個基本步驟:分割、近似代替、求和、取極限)比較煩瑣,所以在實際的計算過程中很少使用。相反地,我們一般利用微積分基本定理來計算求解定積分。

微積分基本定理揭示了導數與定積分之間的聯系——導數與定積分的運算互為逆運算,同時還給我們提供了一個計算定積分的簡單有效的方法。

一般地,如果f(x)是區間[a,b]上的連續函數,并且F'(x)=f(x),那么=F(b)-F(a),這個結論叫作微積分基本定理,又叫作牛頓—萊布尼茨公式。

如果F'(x)=f(x),則(F(x)+c)'=f(x)(其中c為常數),那么,F(x)+c均為f(x)的原函數,要求定積分,關鍵是找f(x)的一個原函數F(x),表1就是常用的基本初等函數f(x)和它的一個原函數F(x)。

表1

分析：根據定積分,找到被積函數的原函數,運用微積分基本定理,即可求解。

點評：本題主要考查了運用牛頓-萊布尼茨公式求解定積分的方法,其中解答時根據定積分公式,找出被積函數的原函數,準確計算是解答的關鍵,著重考查了同學們的運算與求解能力,屬于基礎題。

分析：通過微積分基本定理計算出a,c的值,通過定積分的幾何意義可求出b的值,比較即可得出結果。

點評：本題主要考查利用微積分基本定理和定積分的幾何意義來計算定積分的值。

分析：先將被積函數變形,然后根據定積分基本性質和微積分基本定理,計算即可。

點評：計算定積分的步驟：①先將被積函數變形為冪函數、正弦函數等基本初等函數的和、差等形式;②根據定積分的基本性質進行變形;③分別利用求導公式的逆運算,找到相應的原始函數;④利用微積分基本定理分別求出各個定積分的值,然后求代數之和(差)即可。

例4 若函數f(x)=ln(ex+1)+a x為偶函數,則

分析：由函數f(x)=ln(ex+1)+a x為偶函數,求得,再利用微積分基本定理求解即可。

解：因為f(x)=ln(ex+1)+a x為偶函數,所以f(1)=f(-1),即ln(e+1)+a=解得所以

點評：本題主要考查由已知函數的奇偶性求參數,以及微積分基本定理的應用。已知函數的奇偶性求參數,主要方法有兩種：一是利用：(1)奇函數由f(-x)+f(x)=0恒成立求解,(2)偶函數由f(-x)-f(x)=0恒成立求解;二是利用特殊值：奇函數一般由f(0)=0求解,偶函數一般由f(-1)-f(1)=0求解,用特殊法求解參數后,一定要注意驗證奇偶性。

例5 求曲線y2=2x與直線y=x-4所圍成的曲邊圖形的面積。

分析：先作圖,根據圖形求出交點坐標,以交點的縱坐標y為積分變量,寫出積分。

解：如圖1,在y∈[-2,4]上,直線x=y+4在曲線之上,所以曲線y2=2x與直線y=x-4所圍成的曲邊圖形的面積為

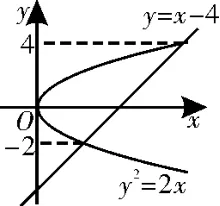
圖1

點評：根據具體情況,選取適當的積分變量,運用微積分定理進行簡便計算。

例6 已知拋物線y=x2-2x及直線x=0,x=a,y=0所圍成的平面圖形的面積為,求a的值。

分析：先作出y=x2-2x的圖像,根據圖像分析可知,要將a分成三類討論圍成區域,當a＜0時,,當0＜a≤2時,,當a＞2時,種情況分別求出a的值,其中一個值舍去。

解：作出y=x2-2x的圖像,如圖2所示。

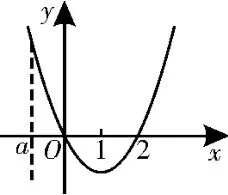
圖2

(1)當a＜0時,,所以(a+1)(a-2)2=0。因為a＜0,所以a=-1。

(2)當0＜a≤2時,所以(a+1)(a-2)2=0。因為a＞0,所以a=2。

(3)當a＞2時解得a=2。因為a＞2,所以不合題意。

綜上,a=-1或a=2。

點評：本題主要考查利用微積分基本定理計算定積分,考查分類討論和數形結合的數學思想方法。由于題目要求圍成圖形的面積,所以首先要畫出圖像,看清楚圍成的圖像是哪一個部分。本題中當a的取值不同時,圍成的圖像不一樣,故分成三種情況分別求解a的值。