函數測試題A 卷

■河南省太康縣第一高級中學

一、選擇題

1.已知3a=5b=1 5,則a,b不可能滿足的關系是( )。

A.a+b＞4

B.a b＞4

C.(a-1)2+(b-1)2＞2

D.a2+b2＜8

2.已知a,b均為正實數,函數y=aex+b的圖像過點(0,1),則的最小值為( )。

A.2 B.3 C.4 D.5

3.素數也叫質數,部分素數可寫成“2n-1”的形式(n是素數),法國數學家馬丁·梅森就是研究素數的數學家中成就很高的一位,因此后人將“2n-1”形式(n是素數)的素數稱為梅森素數。已知第2 0個梅森素數為P=24423-1,第1 9個梅森素數為1,則下列各數中與最接近的數為( )。(參考數據:l g2≈0.3)

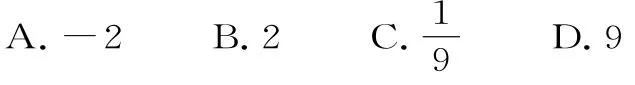
A.2 B.4 C.6 D.8

6.已知函數f(x)=ex+e4-x,則( )。

A.f(x)在(-∞,2)上單調遞增,在(2,+∞)上單調遞減

B.f(x)在(-∞,2)上單調遞減,在(2,+∞)上單調遞增

C.函數f(x)的圖像不關于直線x=2對稱

D.函數f(x)的圖像關于點(2,0)對稱

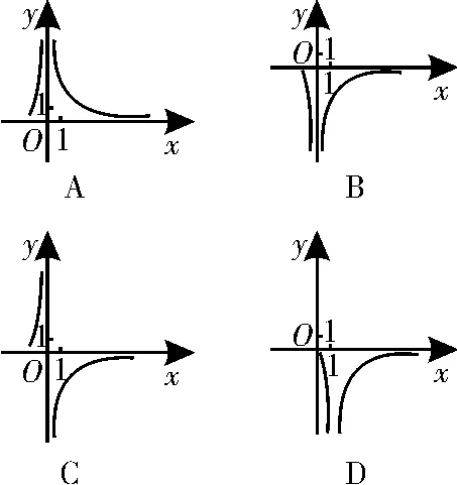
圖1

8.函數y=f(x-1)的圖像關于點(1,0)對稱,當x∈(0,+∞)時,f(x)+x f'(x)＜0成立,若,則a,b,c的大小關系是( )。

9.若函數f(x)=loga(x+1)(a＞1)的圖像與函數y=g(x)的圖像關于原點對稱,且x∈[0,1)時,不等式2f(x)+g(x)≥m2-m恒成立,則實數m的取值范圍是( )。

10.已知函數f(x)=l g([x]-x),其中[x]表示不小于x的最小整數,則關于函數f(x)的性質表述正確的是( )。

A.定義域為(-∞,0)∪(0,+∞)

B.在定義域內為增函數

C.周期函數

D.在定義域內為減函數

11.已知冪函數f(x)=(m-1)2·xm2-4m+2在(0,+∞)上單調遞增,函數g(x)=2x-t,?x1∈[1,6)時,總存在x2∈[1,6)使得f(x1)=g(x2),則t的取值范圍是( )。

A.? B.t≥2 8或t≤1

C.t＞2 8或t＜1 D.1≤t≤2 8

12.已知函數f(x)=函數g(x)=|2f(x)-m|-1,且m∈Z,若函數g(x)存在5個零點,則m的值為( )。

A.5 B.3 C.2 D.1

二、填空題

14.設實數a,b分別滿足方程3a2+6a+1=0和b2+6b+3=0,且a·b≠1,則a-3a b-1+b-1的值為

三、解答題

17.化簡或求下列各式的值。

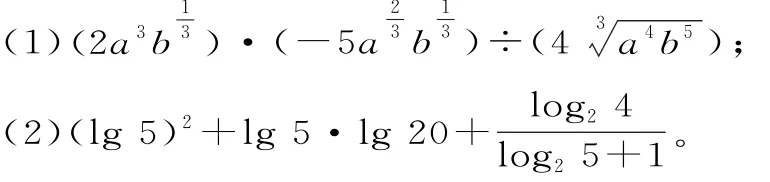
18.已知函數f(x)=ax+b(a＞0,a≠1),其中a,b均為實數。

(1)若函數f(x)的圖像經過點A(0,2),B(1,3),求函數的值域;

(2)如果函數f(x)的定義域和值域都是[-1,0],求a+b的值。

19.為了在夏季降溫和冬季取暖時減少能源消耗,業主決定對房屋的屋頂和外墻噴涂某種新型隔熱材料,該材料有效使用年限為2 0年,每毫米厚的隔熱層建造成本為6萬元,且每年的能源消耗費用H(萬元)與隔熱層厚度x(毫米)滿足關系(0≤x≤1 0),設f(x)為隔熱層建造費用與2 0年的能源消耗費用之和。

(1)請解釋H(0)的實際意義,并求f(x)的表達式。

(2)當隔熱層噴涂厚度為多少毫米時,業主所付的總費用f(x)最少?若此時與不建隔熱層相比較,業主可節省多少錢?

20.冪函數為什么叫“冪函數”呢?冪,本義為方布。三國時的劉徽為《九章算術·方田》作注:“田冪,凡廣(即長)從(即寬)相乘謂之乘。”冪字之義由長方形的布引申成長方形的面積;明代徐光啟翻譯《幾何原本》時,自注曰:“自乘之數曰冪”。冪字之義由長方形的面積再引申成相同的數相乘,即xn。

圖2

(1)判斷函數g(x)=f(1+x)+f(1-x)的奇偶性并求其值域;

(2)若關于x的方程f(x2-t x+8)=2在[1,4]上有解,求實數t的取值范圍。

22.已知函數f(x)=(a2-2a-2)logax是對數函數。

(1)若函數g(x)=loga(x+1)+loga(3-x),討論g(x)的單調性;