陸基導彈的數學模型預算法設計*

王少純 王哲峰 陳昱辰 劉艷龍 張馨丹

（1.沈陽航空航天大學航空宇航學院 沈陽 110000）（2.沈陽大學環境工程學院 沈陽 110044）（3.沈陽航空航天大學航空發動機學院 沈陽 110000）

1 引言

隨著我國國防力量的發展，彈道導彈已經成為捍衛祖國主權的戰略力量。當導彈在飛行時，其質心在空間內會形成一條運動軌跡，這條軌跡就是通常所說的基準彈道，我們通過對彈道的分析研究可以提高導彈的性能和命中率。

因此在設計導彈時，要經過彈道分析掌握導彈的運動規律，進而選擇正確的結構參數、選擇合適的飛行彈道以及進行正確精準的彈道計算、進而評定導彈的基本性能參數、同時也能夠為導彈的飛行試驗提供需要的理論彈道參數數據。導彈彈道按照坐標系不同劃分為絕對彈道和相對彈道。其中絕對彈道是建立在慣性坐標系中的導彈彈道模型。例如地空導彈、岸艦導彈、近程的地地導彈。本文通過對導彈飛行過程中位置參數和艦船運動時的位置參數進行分析，建立模型，確定導彈的軌道模型并解決相關問題。

2 導彈打擊目標的具體分析

導彈的制導過程是一個復雜的過程，在這一過程中，可能會受到大氣環境、攻擊參數和對方反導系統攔截等很多條件的干擾。本文只考慮導彈本身軌跡的改變和攻擊目標（航母）的運動以及地球的自轉及曲率影響。

當目標為靜止狀態時，通過參數方程對三維空間內的彈道進行參數化分解，將導彈彈道這一復合的軌跡分解成為三個相互垂直的分運動。通過對三維位置點的分解，可以得到三個方向關于時間的速度參數方程，并代入地球自轉［1]，地主曲率和變軌技術等產生的影響因素，即可描繪導彈的彈道軌跡。

當目標具有一定運動速度，且運動方向與導彈三個分運動方向其中一個方向在同一直線上，因此只需要在彈道軌跡的基礎上進行相關方向運動參數的修改即可。在此問題中，我們只需要考慮導彈第二階段的飛行，即發射中段的導彈飛行模型即可達到跟蹤的目的。以拋物線的頂點為起點，完善導彈中段的動態飛行模型與算法。

通過對導彈發射點和航母起始點在地球表面相對位置的確定，得到如下的相對位置圖。

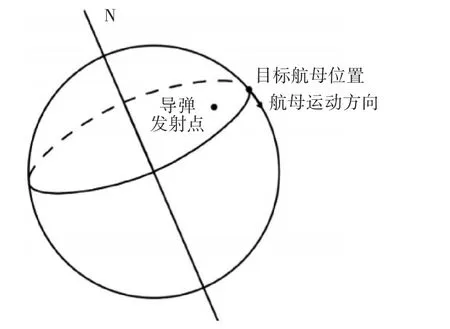
圖1 導彈發射點與航母在地球上位置確定

通過二者的坐標和在途中的相對位置可以看出，在初始時刻，二者的維度不同。因此，即使航母不運動，導彈若命中目標，也需要跨越緯度飛行。同時導彈必須要向前飛行和向上方飛行以升高飛行高度。我們可以將導彈的飛行軌跡看成一個三維的曲線［2]。

對導彈的運動建立三維模型，將其運動軌跡分解為豎直（z）方向，東西（x）方向，南北（y）方向。

若從上空觀測導彈的飛行軌跡，會發現如圖2（a）中鎖死的彈道軌跡，從某一緯度所在平面觀測，會發現如圖2（b）中所示的彈道軌跡。

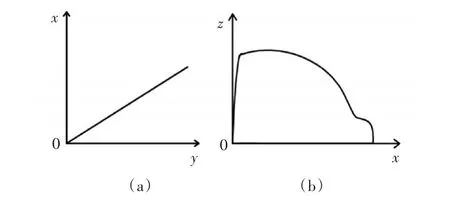
圖2 不同角度的導彈彈道軌跡

導彈在發射后的運動軌跡可分為三部分［3]，即發射段、中段和末段。如圖3所示，導彈在發射段受重力和推進器產生的推力作用（空氣阻力忽略不計）做拋物線式運動；在發射中段，導彈的運動可再分為兩部分，一是只受重力和空氣阻力作用的自由彈道，二是在衛星調控的基礎上，受到重力和空氣阻力共同作用的再入彈道；當航母進入導彈的打擊范圍，導彈進入末段軌跡，自主打擊目標。

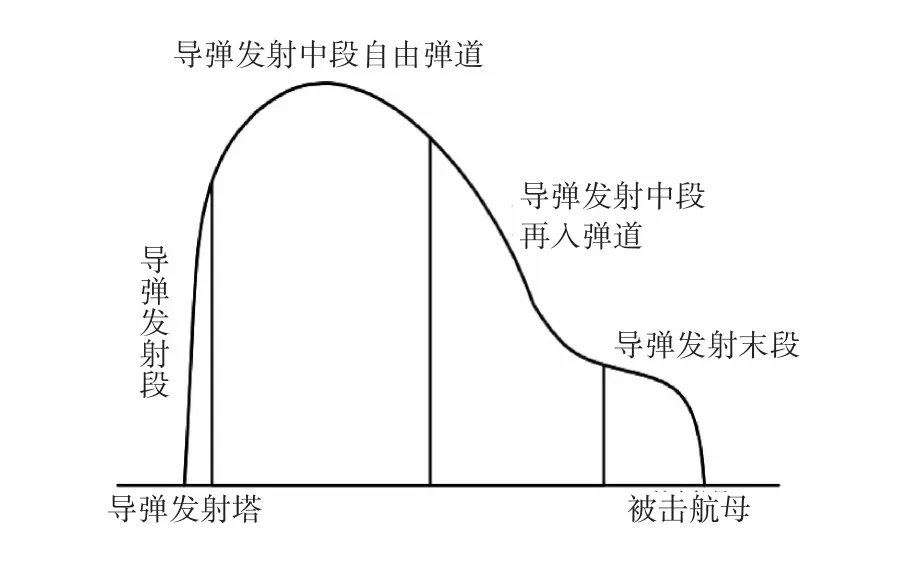
圖3 導彈發射全程示意圖

將導彈在x，y和z方向上的運動均看成為多次變加速運動的合運動，得到如下的運動方程。

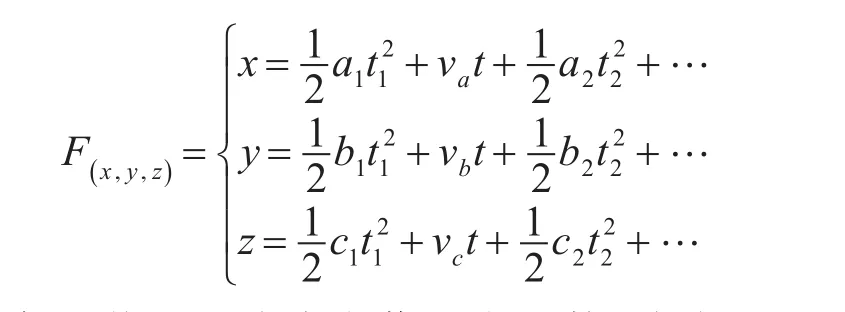
將導彈的運動分為若干個函數，式中的an，bn，cn等分別為導彈在第n段中x、y、z方向上的加速度，tn為導彈在第n段所經過的時間［4]。

以導彈發射車為坐標原點，xi為原點與地球的切線，方向指向正東方向，xi軸和zi軸相互垂直，方向豎直向上。導彈在發射段時，由于只受燃料推力，空氣阻力和重力的作用，其軌跡可以簡化為拋物線（y等于0）。在o-xizi坐標系內可以建立其彈道方程：

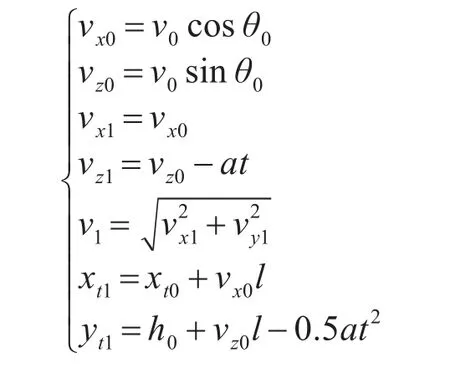
式中v0，h0分別為導彈發動機關機時的速度和高度，xt0為導彈在發動機關機時，在平面坐標系o-xizi上的橫坐標，vx0，vz0分別為導彈發動機關機處，速度在坐標系上沿oxi軸和ozi軸上的分量，vx1，vz1和xt1，zt1分別為導彈于發射段時，在坐標系上的速度和位移分量，θ0為導彈發射段開始時的傾角（極小），t為導彈在發射段的運行的時間，a為導彈在上升時所受到的加速度矢量和，H為導彈飛行高度［5]。

在導彈的中段，導彈可分為自由彈道和再入彈道兩個階段，自由彈道是近似拋物線的運動軌跡，再入彈道為導彈從脫離拋物線到再一次進入到大氣層后的運動軌跡。

導彈的自由彈道可以看成是導彈質心運動和繞心運動的結合。在中段，導彈的運動微分方程應由運動學方程，控制方程，質心運動方程和繞質心運動的動力學方程共同組成。我們同樣以導彈發射車為坐標原點，研究導彈姿態運動方程［6]。

導彈質心運動方程可由動力學方程和質心運動方程積分求得：

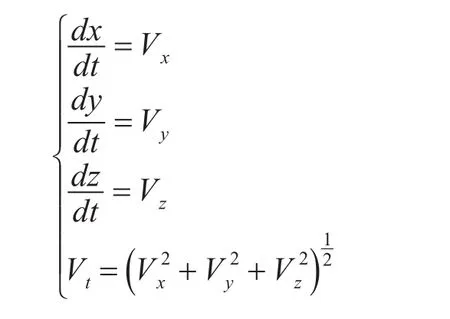
導彈姿態方程可以利用導彈轉動角速度ω1在坐標系的投影方程：

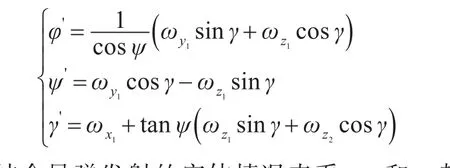
結合導彈發射的實體情況來看，ψ和γ都是很小的量，可以近似認為 sinψ≈ψ，sinγ≈γ，cosψ≈cosγ≈1。

與導彈進入自由彈道相比，導彈在進入再入彈道后所受的力主要為大氣產生的阻力和導彈自身所受的重力。所以在以導彈發射車為坐標原點的三維坐標系中，可以建立再入彈道的微分方程：

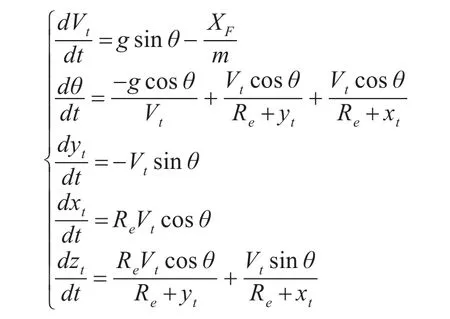
式中：m為導彈去掉推進器后的彈頭質量；vt為導彈質心在三維坐標系上速度的模；XF為空氣阻力，并且：

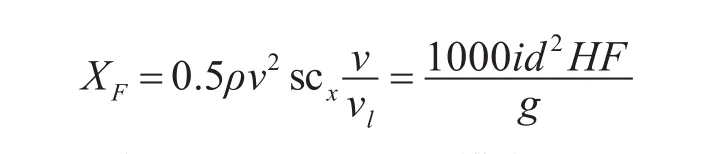
式中ρ為空氣密度；s為導彈橫截面積Rb為導彈底部半徑；d為導彈最大直徑；vl為音速，v為導彈速度；i為彈性系數，該系數與導彈外形有關；為馬赫數對應的標準阻力系數；F為阻力函數，另：

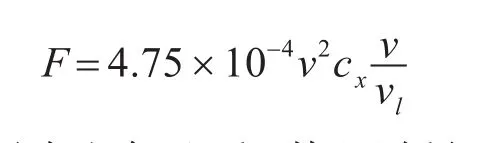
H為無因次空氣比重，其跟隨導彈高度變化的經驗公式為

當高度小于9300m時：

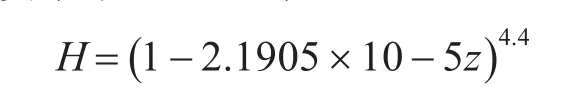
當高度大于等于9300m時：

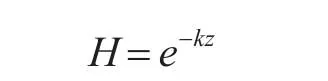
式中：k=0.0001。

在導彈中段的自由彈道結束后，導彈馬上進入再入彈道，結合自由彈道和再入彈道，可以建立方程為

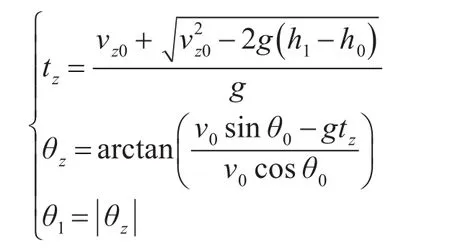
式中：h1為導彈結束自由彈道時的高度；θz為再入角；tz為導彈結束自由彈道時的時間，θ1為導彈進入再入彈道時的傾角。

考慮到在制導導彈的打擊過程中，對方的反導系統會進行攔截，故找出有效的行進軌跡來對導彈進行變軌處理，來最大化降低攔截的可能性十分必要［7]。機動變軌技術是導彈在飛行中可隨時改變其彈道，以躲避敵方反導防御系統攔截的一種突防技術，通常分為全彈道變軌和彈道中末段變軌兩種。因為導彈發射初期是在己方國土內，所以敵人很難如此迅速的檢測到發射信號，并且導彈在彈道末端是以二十秒內保持1000m/s的超音速進行俯沖，在這種高速短時狀態下敵人很難精確對導彈進行攔截。因此，為節約發動機燃料和實現最高效的精確打擊，我們將變軌技術只應用在中段。現階段常用的變軌軌跡為蛇形機動和s形機動，其變軌原理均是有自帶的小火箭在短時間內產生推力而完成。

變軌過程加速度是由推力T大小，方向單位向量uT和導彈的質量m決定的，即

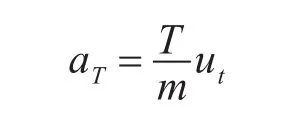
式中導彈的質量隨燃料燃燒而減小，T可以表示為

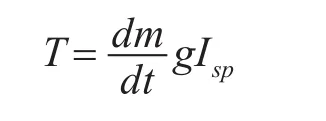
由上可得，推力方向也就是變軌方向是決定推力大小等參數的決定因素。所以我們研究出了基于大風級下的海浪波動模型。此模型通過模擬在大風級自然風下海浪的波形，來形成導彈的變軌軌跡。此軌跡具有隨機性強，風級固定下穩定的特性，所以對最終打擊精度不會有太大誤差。我們將海浪高度在坐標系內的變化用一個三元函數來表示［8]：

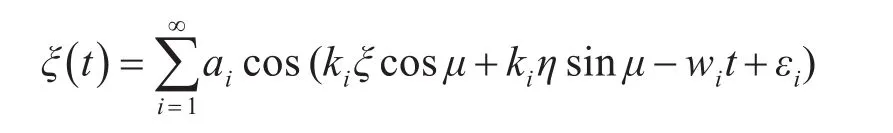
其中，ai，ki，wi，εi分別為第i次諧波的波幅，波數，角頻率，初相位。

我們知道導彈變軌是由導彈攜帶的多個矢量火箭發動機，產生的脈沖推力來完成，在變軌過程中由于減少了前進方向的速度分量，會增加飛行時間。為了降低導彈負擔，和避免貽誤戰機，并我們將海浪模型簡化成二維問題。

這種“二元不規則波”可表示為

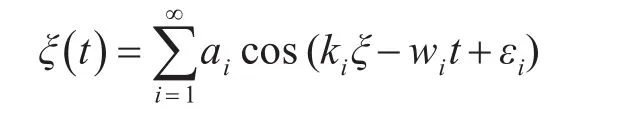
3 反導導彈殺傷區模型

從航空母艦發射的反導導彈的殺傷區是其不低于某一給定概率殺傷目標的空間范圍，它主要是有反導系統的火控系統的參數決定，并且需要同時滿足以下四個不等式。這表示出的區域就是反導系統的有效殺傷區。其中我們不考慮時間對相遇的影響［9]。

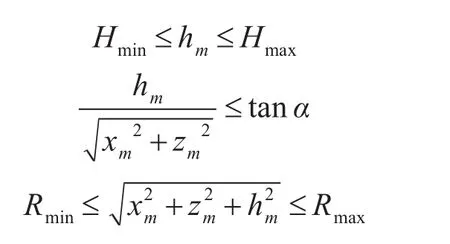
式中：Qm為OX與正北方向夾角。

我們可以把地球看成是一個繞地軸自西向東旋轉的球體，由于它的旋轉運動，地球表面上從兩極到赤道上，各點的運動速度是隨當量半徑的增長而增大的。越靠近地球兩端，表面的運動線速度越大，反之越小。而且，在同一維度上，海拔高度的不同也會導致線速度的偏差，比如說摩天大樓樓頂的線速度要大于底座的線速度。所以計算導彈軌跡時，如果不計算自轉產生的影響，那么在導彈的長距離跨經緯度的飛行過程中，就會因為這兩方面因素的影響，最終會導致無法精確打擊目標。

這其中一個重要參數為偏近角E

平進點角：

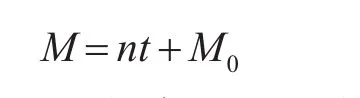
式中：M0=E0-esinE0相當于T=0時的平近點角。

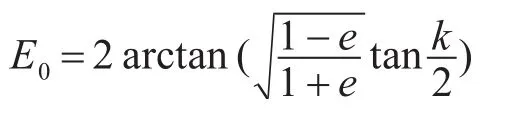
從開普勒方程可知，如果已知偏近點角E求M非常容易，但是在已知M的條件下求E，這是一個超越方程，用微分迭代比較容易求解。

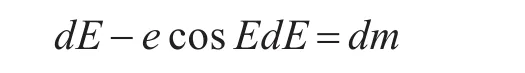
即

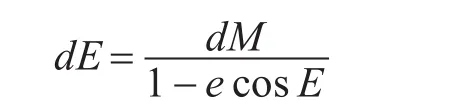
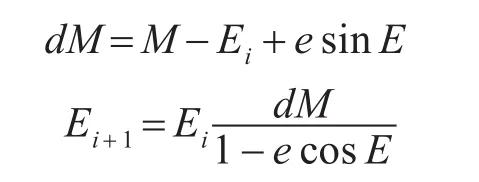
收斂條件：

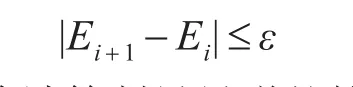
之后為精確計算制導導彈的軌道和打擊點，我們在兩個慣性參考系中，選擇對發射段結束的分離點進行分析。A坐標系原點為地球質心，X，Y，Z軸滿足右手法則且固定在地球上；B坐標系的X，Y，Z三軸的指向和A相同，但是它們隨地球自轉而旋轉，即三軸的指向在不斷變化。由上述兩個坐標系的定義可得：1）在發射段結束時刻，A坐標系中導彈的位置矢量與B坐標系的導彈位置矢量相同［10]，即：rKA=rKB，rKA和rKB的兩個位置分量分別表示關機點經度和關機點緯度，K表示關機點。2）導彈在坐標系A，B中的速度不一樣。速度矢量差為地球自轉速度在該高度引起的牽連速度，用VKe來表示。導彈在A坐標系中的速度矢量VKA（Vx，Vy，Vz）為已知參數，則在B坐標系中的速度矢量VKB為

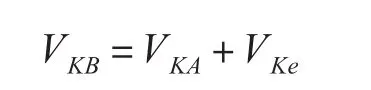
地球自轉轉向為自西向東，其角速度為w，所以，其引起的牽連速度VKe的方向沿K點自西向東，大小為ωrKcosΘk，這里Θk為K點緯度，rK為K點

賦初值：

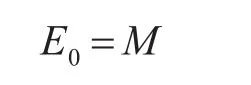
迭代公式：到地心的距離。

因此，考慮地球自轉的導彈速度為

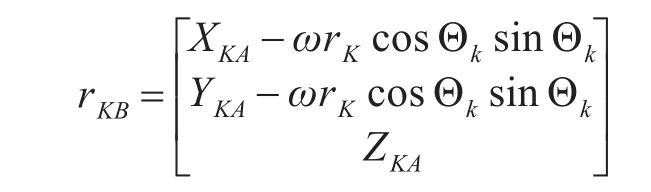
XK，YK，ZK是rKA的直角坐標形式。因此，當不考慮地球自轉時，關機點的速度參數為rKA，rKA，而上述驗證的考慮地球自轉時的關機點參數為rKA，rKB。

如果把地球視為一個半徑為6300km的球體，那么它的曲率不能忽略。

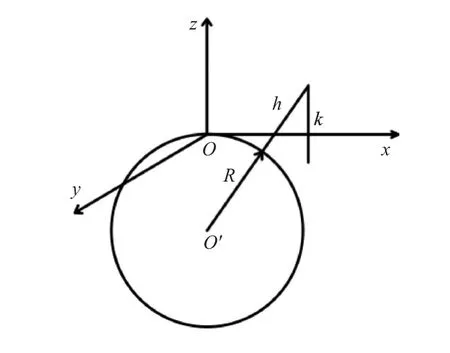
圖4 地球曲率對導彈打擊點的影響

不考慮地球曲率時，導彈平在飛段的彈道傾角θ≈0°，而實際上導彈存在彈道傾角θ'：

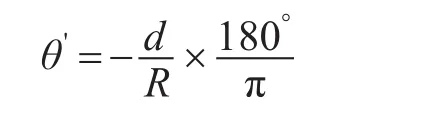
式中，d為導彈的飛行距離。

當導彈飛行340km時，θ'-θ=-3.09°，所以地球曲率對導彈打擊點的影響不可忽略。

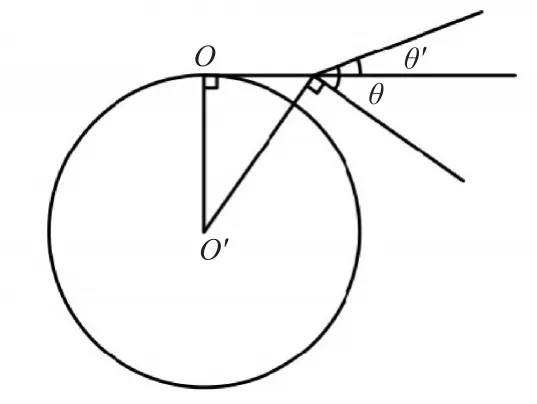
圖5 俯仰角示意圖

因為近程導彈的主軸不跟蹤地球曲面［11]，導彈發射時決定其運動狀態，而且導彈的各方向角是以各向主軸作為基準測出的，所以導彈的各方向角的定義取決于以上所定義的坐標系。因為導彈發射時的水平面與主軸始終成一定角度，所以導彈的傾角始終是導彈發射時的水平面與彈軸的夾角(?)，而不是和所處位置水平面的夾角(?')，如圖3所示。所以只需假設原始坐標系是慣性參考系，根據導彈距離地表的高度(h)及其變化率(h')來模擬無線電高度表測得的導彈高度及其變化率，將其加入到導彈的高度控制回路中，并且把重力加速度改為g'，建立考慮地球曲率的導彈彈道模型：

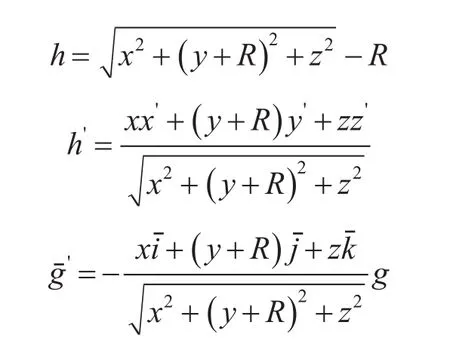
綜上我們可以得出導彈打擊模型為

通過對導彈運動的三維建模進行分析求解，我們已經得出了導彈打擊靜止點的運動方程。當航母向正南方向（y方向）以速度Vk勻速運動時，在上一個模型基礎上，給導彈運動方程添加一個y方向的速度Vk即可得到問題二的模型［12]。

導彈質心運動方程可由動力學質心運動方程積分得：

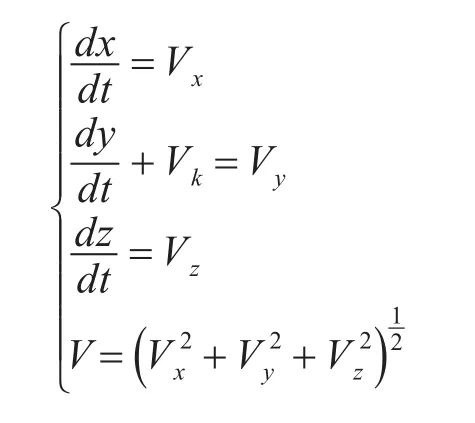
導彈姿態方程可以利用導彈轉動角速度ω1在坐標系的投影方程：

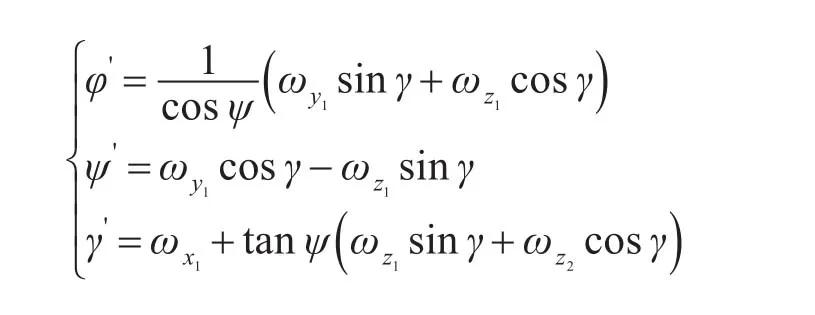
與問題一相同，結合導彈發射的實體情況，ψ和γ都是很小的量，可以近似認為sinψ≈ψ，sinγ≈γ，cosψ≈cosγ≈1。

在目標移動時，導彈的中段自由彈道運動方程為

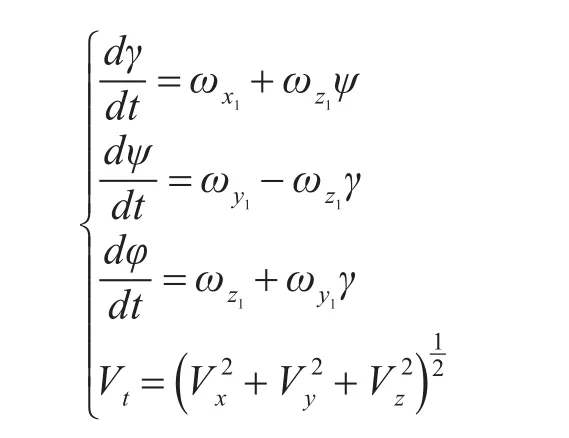
導彈進入再入段后，除y方向上加的勻速運動外，其運動方程和問題一相同，即：

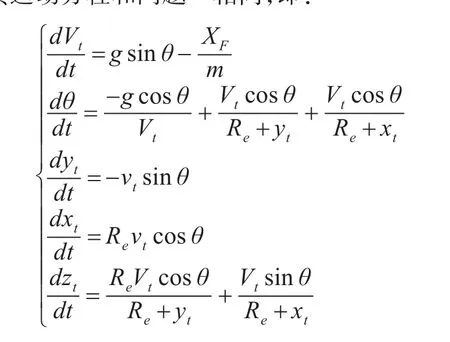
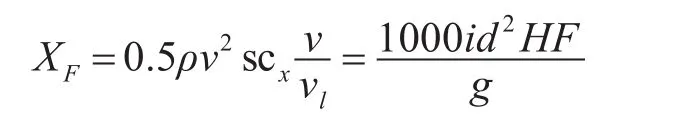
式中：m為導彈去掉推進器后的彈頭質量；vt為導彈質心在三維坐標系上速度的模；XF為空氣阻力，并且：式中ρ為空氣密度；s為導彈橫截面積Rb為導彈底部半徑；d為導彈最大直徑；vl為音速，v為導彈速度；i為彈性系數，該系數與導彈外形有關為馬赫數對應的標準阻力系數；F為阻力函數，另：

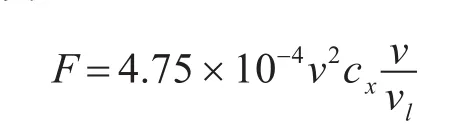
H為無因次空氣比重，其大小跟隨導彈高度變化的公式為

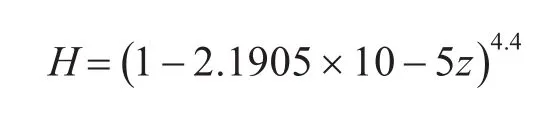
結合自由彈道和再入彈道，建立方程：

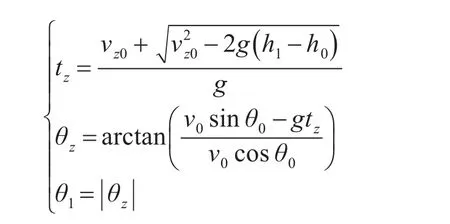
式中：h1為導彈結束自由彈道時的高度；θz為再入角；tz為導彈結束自由彈道時的時間，θ1為導彈進入再入彈道時的傾角

所以在目標航母以Vk的速度向南方向行駛時導彈的中段運動方程為

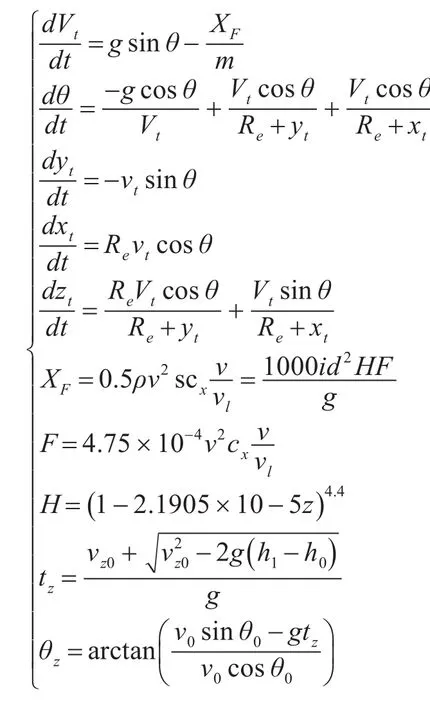
4 結語

該模型針對打擊靜止目標時的軌跡和打擊靜止目標時的軌跡均進行了數字化分析，并結合于公式，建立了全面的導彈打擊和預防攔截模型，增加了精準率并減小了偏差。同時，考慮到到溫度，天氣，空氣質量等對本模型的干擾，均將其設為干擾因子，計算比例后帶入模型。