山區河流造床流量計算探討
(四川大學 水利水電學院,四川 成都 610041)
造床流量是河道造床過程與多年流量過程的結合產物,是一種長期的平均效應,對河床形態起著控制作用。其本質上同河道來水量及其過程和與之相應的來沙量及其過程相關。需要注意的是,造床流量不是最大洪水流量,因為這種流量作用時間短;它也不是枯水流量[1],因為這種流量又過小。因此造床流量是一個偏大但又并非最大的流量[2]。合理確定造床流量[3],對河道整治規劃設計,穩定河寬的確定以及沖刷深度的計算有著重要幫助。實際工作中常采用馬卡維也夫法和平灘流量法確定造床流量。此外,還有一些經驗方法,如黃河水利委員會水利科學研究所研究得出的造床流量和多年汛期平均流量的關系方程[4];吳保生等[5]指出,平灘流量不能簡單地與造床流量混為一談。然而對于少沙河流,平灘流量與造床流量卻比較接近[6],如長江中下游各河段造床流量與平灘流量是基本一致的[7]。
這些研究成果普遍只適用于平原丘陵地區的沙質河道。目前,對山高坡陡,自然比降大的山區河道的研究還不充分,特別是河道巖坡及兩側大多屬于沖積層的情況下,大都存在土層厚、土質松散、岸坡較陡的現象[8],造床流量在工程設計應用中往往存在偏差。因此本文以黑水河下游為例,探討適應山區河流造床流量的計算方法。
1 研究區概況
研究區位于四川省阿壩州境內,海拔均在1 500 m以上,具有地質條件多變,氣候條件惡劣等特點。黑水河地處橫斷山脈中段北端,岷山與邛崍山交匯處,全長122 km,流域面積7 240 km2,水系呈羽狀發育。河流穿行于崇山峻嶺之中,下游河段河谷較為開闊,多呈“U”型,河谷兩岸高山植被稀疏,歷史上曾發生多次崩塌滑坡泥石流,因而河底多碎塊石、卵石和漂石。河岸土層較厚,植被以灌木為主,灘地多集中于右岸,河道較為順直但存在少數不規則邊坡改變河流的流態。黑水河流域及下游河道見圖1~2。
2 造床流量的多種計算方法
根據造床流量的相關研究,計算方法主要為馬卡維也夫法、平灘流量法、洪峰頻率法3種。本文旨在分析水流與河床相互作用達到穩定狀態下的造床流量,以建立河相關系,故盡可能選取長系列資料來進行計算。研究區有一處水文站-沙壩水文站,該站記錄有1956~2017年共62 a的年洪峰流量、輸沙率、徑流等資料,用這些資料進行相關計算。

圖2 黑水河下游河道Fig.2 Channel of lower Heishui River
2.1 馬卡維也夫法
馬卡維也夫法[9]是把分析時段內的日流量劃分成一系列的等區間;確定落入每一區間的流量次數占整個分析時段內觀測次數的頻率P,并計算落入每一區間的流量系列的平均值Q,見圖3。
由每一區間的Q,根據水位流量關系反推水位,再參考斷面平灘水位,確定各流量區間相應的灘地作用系數σ;河道比降J可通過Q-J曲線查得也可實測得到;m為指數(詳見2.1.1)。最后計算每一流量區間的造床流量作用值σQmJP;點繪系列Q和σQmJP關系曲線,曲線峰值對應的流量即造床流量。

圖3 各頻率下Q平均值Fig.3 Average Q value at each frequency
2.1.1m值的確定
馬卡維也夫法中的m值源于水流輸沙率Qs和流量Q,根據有關研究[10],可采用多年月均流量與多年月均輸沙率關系確定m值。統計分析表明,黑水河下游多年月均Qs~Q之間相關關系較好,表1為多年各月平均輸沙率與流量。

表1 多年各月平均輸沙率與流量Tab.1 Monthly average sediment transport rate and runoff over years
圖4為沙壩站多年月均輸沙率與多年月均徑流量的關系曲線,其中R2=0.88,擬合度較好。由此得到m值為3.227 5。
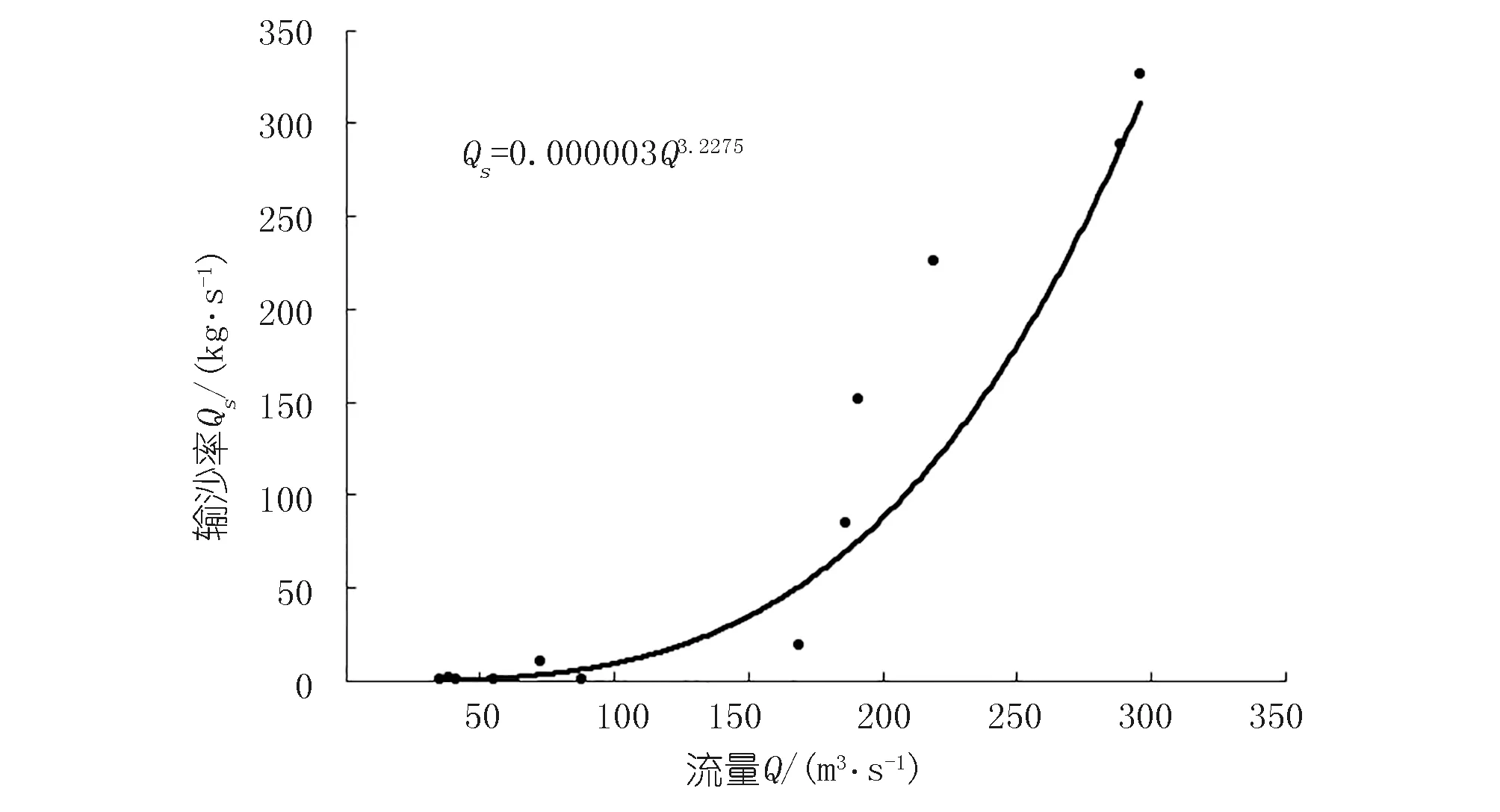
圖4 沙壩站流量-輸沙率關系曲線Fig.4 Flow-sediment transport rate curve at Shaba station
2.1.2馬卡維也夫法計算結果
本例中σ值取1,J取0.003 56,m為3.227 5,將圖3中的Q和P代入公式σQmJP得到沙壩站的σQmJP-Q曲線,見圖5。

圖5 沙壩站σQmJP-Q關系曲線Fig.5 σQmJP-Q curve of Shaba station
圖5的關系曲線存在兩個明顯的主峰,以“峰值1”和“峰值2”表示。這在研究區其他水文站的計算中也有類似現象,只是峰值1有時并不是σQmJP的最大值。因此峰值序號與峰值大小無關,而是指若干主峰出現次序。
由圖5可以看出,山區河流流量-輸沙率關系曲線擬合度較平原地區弱[11],用馬卡維也夫法計算造床流量時m取值一般大于平原地區(平原地區m取2[12])。這是由于山區河道比降大,導致的輸沙率較高,以及輸沙率對流量的響應較為敏感,同時山區徑流量的波動較大(本例所選資料的Cv為0.79)。
取圖5曲線中兩個峰值所對應的流量221,338 m3/s作為計算結果。
2.2 平灘流量法
平灘流量通常指某一斷面的水位與灘唇齊平時通過該斷面的流量,平灘流量值取決于來水來沙條件和斷面的形態。具體方法為:首先根據水文站每年實測大斷面資料確定灘唇的高程從而確定平灘水位,再根據當年水位流量關系曲線確定平灘水位對應的流量,作為平灘流量。
為便于研究,將黑水河下游河段設立的11個斷面,記為CS1~CS11,各斷面的歷年平均平灘流量見表2。
從表2中可以看出,各斷面平灘流量差異較大,這是因為各斷面地貌形態不同,如CS11、CS10、CS6等斷面因為河道較寬,平灘流量顯著偏大。因此使用這種方法應謹慎,因為山區河道往往并不順直,犬牙交錯的邊灘對平灘流量計算的影響較大。
取各斷面平灘流量的平均值957 m3/s作為該河段的整體平灘流量,這相當于該水文站處10%~20%頻率下的洪峰流量。

表2 黑水河下游平灘水位高程和平灘流量Tab.2 Water level and flow at beach elevation in the lower Heishui River
2.3 洪峰頻率法
在一些研究和工程設計中,通常使用2 a一遇洪峰流量來代替造床流量。可用水文站多年系列年最大洪峰流量求得該河段對應頻率下的流量,將62 a的洪峰流量降序排列,根據序號和歷史洪水計算出每個流量值的頻率,點繪至頻率格紙上得到經驗點據,由此計算出平均值、變差系數、偏態系數并得到皮爾遜Ⅲ型理論曲線[13],調整參數使理論曲線適應經驗點據,見圖6。
通過理論曲線查得2 a一遇頻率(50%)下的洪峰流量。本例中為739 m3/s。
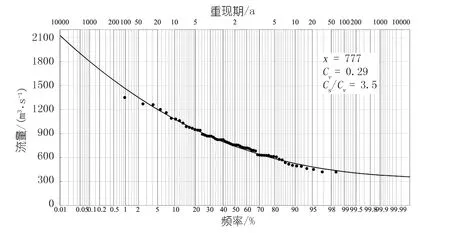
圖6 洪峰頻率法P-Ⅲ型曲線Fig.6 P-Ⅲ curve of Peak Frequency Method
3 結果驗證
為探討何種方法最適用于計算山區河流造床流量,本文采用穩定河寬這一指標來檢驗。穩定河寬是河勢穩定計算中的重要指標,本文提出用歸一化方法來比較計算得到的穩定河寬是否與現有河道寬度相符[12],來判別哪種方法最優。穩定河寬計算公式為
Bs=KQ6/11/(n32/33·J3/11)
(1)
式中,Bs為橫向穩定河寬,m;系數K取1/10030/33;Q為造床流量,m3/s;J為比降,本例中取0.003 56;n為糙率,本例中取0.04。
歸一化方法為

(2)
式中,Bmin和Bmax分別代表實際河道最窄處和最寬處的寬度,本例中Bmin取30 m,Bmax取60 m。
由3種方法得到的黑水河下游造床流量及其對應的穩定河寬和α值見表3。

表3 3種方法計算的造床流量、穩定河寬、α值Tab.3 Calculated flow rate of stoma, width of stable river and value of α by three methods
通常穩定河寬不會大于河道最大寬度,且根據歷史資料,黑水河下游河勢較穩定,即α值應介于0到1并靠近0為宜。從表2可知:平灘流量法和洪峰頻率法計算的穩定河寬和α值顯著偏大,不符合實際情況。馬卡維也夫法的計算結果最接近實際值,并且用峰值1對應的流量計算的結果要好于峰值2的計算結果。因此針對山區河流,應考慮用馬卡維也夫法峰值1對應的流量來進行河勢穩定分析。
在一些研究中[12],偶見用多年平均年徑流量來代替造床流量,用該地區多年平均年徑流量(140 m3/s)計算的α值為0.208,與馬卡維也夫法峰值2對應的流量計算的α值接近。因此,在山區用多年平均年徑流量代替造床流量也是可行的,同時也簡化了計算流程。
幾種方法的對比結果見表4。

表4 幾種方法的對比Tab.4 Comparison of several methods
4 結 論
本文旨在從3種不同造床流量的計算方法中找出較適用于山區河流造床流量的計算方法。對造床流量求得的穩定河寬與實際河寬進行歸一化處理,取得主要成果如下。
(1) 馬卡維也夫法σQmJP-Q關系曲線峰值1對應的流量最接近實際造床流量,因此該法在山區河勢穩定分析中值得推廣。同時發現該法中山區流量-輸沙率關系曲線擬合度較平原地區弱,山區m值也普遍大于平原地區[13-14]。
(2) 可考慮用山區多年平均年徑流量代替造床流量,以簡化計算流程[15]。
馬卡維也夫法對資料的要求較高,而山區河流往往缺乏資料,如何優化該算法以降低過多資料的依賴還需要學者進一步研究。

