一道競賽試題的多解及變式*

四川內江師范學院數學與信息科學學院 (641112)

賀鋅菠 劉成龍

一、問題及簡評

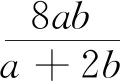
簡評:問題是數學的心臟，問題是研究的核心.好的數學問題能誘發思考、發展思維、啟迪智慧.賽題是一個好問題，是研究的好素材.

(1)問題具有數學美：問題敘述簡潔，富含簡潔美；(2)問題解答視角寬：學生能利用從三角換元、函數法、重要不等式法、向量法、方程法、待定系數法等多個視角解答，既能開拓學生的視野，同時為求異思維的形成提供了良好的素材；(3)問題可變程度高：問題可從“構造原件”、“關聯結構”、“元素狀態”等視角得到一系列變式；(4)問題考查素養多：問題的解答需要學生具備邏輯推理、數學運算、數學建模等多種素養.

二、解法探究

問題解決是數學活動的基本形式和主要內容.正如數學家哈爾莫斯說：“數學家存在的主要理由是解問題，數學的真正組成部分是問題和解”.下文從不同的視角解答賽題.

視角1 三角函數法

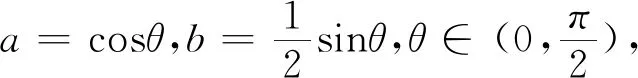
點評：解法1運用三角換元法實現了雙變量到單變量的轉化.

視角2 函數法

點評：解法2、3、4均通過構造函數來解答，不一樣的是所構造函數不同：解法2構造的函數需借助導數來得到單調區間；解法3構造了雙勾函數，其單調區間學生比較熟悉，不需要求導；解法4構造了學生熟悉的二次函數求解.

視角3 重要不等式法

點評：通過對分式等價變形，借助均值不等式求解是此類問題的基本解法.

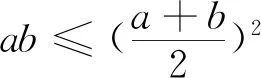
視角4 向量法

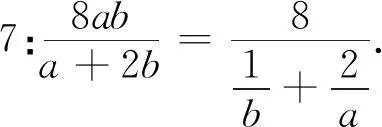
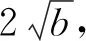
視角5 方程法

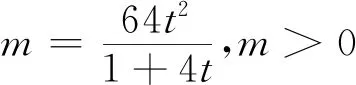
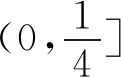
點評:解法8的關鍵是將問題轉化為一元二次方程在區間根的分布問題.

視角6 待定系數法

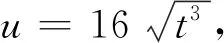
三、問題變式

問題變式是指相對于某種范式，不斷變更問題情境或改變思維角度，使問題的非本質屬性時隱時現，而問題的本質屬性保持不變的思維方式.[1]不斷地變更數學問題中的情境或改變思維的角度，變換問題中的條件或結論，轉換問題的形式或內容，配置各種實際應用的環境等，以期暴露問題的本質特征或內在聯系.[2]下面從問題的“構造原件”、“關聯結構”、“元素狀態”[3]三個方面進行問題變式，引導學生挖掘賽題的本質屬性.

1.變“構造原件”

引入新元素“λ”，且λ>0可得：

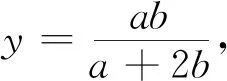
點評：通過引入新元素“λ”，改變問題的組成“原件”，得到一個新的問題.新問題與賽題在實質上沒有改變，變的僅是ab的取值范圍.

基于變式1，引入新元素“μ”，可得：

2.變“關聯結構”

將賽題中的ab移入條件等式，可得：

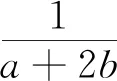
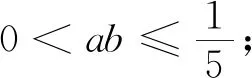
點評：改變ab在原問題中的位置，以改變問題的“關聯結構”，將ab作為條件的組成部分.

基于變式4，引入新元素“λ”，且λ>0可得：

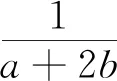
3變“元素狀態”

將元素a和b范圍擴大為實數，可得：

變式6 已知實數a和b，且4a2+ab+b2=1，則a+2b最小值為-2，最大值為2.

點評:改變元素a和b的狀態，將正數a、b擴充為實數，此時不滿足基本不等式的使用條件，無法直接用基本不等式求解,并且a+2b無法直接與條件建立關系,所以考慮從待定系數法求解.

基于變式6，引入新元素“λ”和“μ”，且λ>0可得：

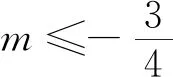
變式8 已知實數a和b，且4a2+2μab+b2=λ，當μ∈(0,1)時，a+μb最小值為

通過對賽題的解法探究及多層次變式，巧妙地把賽題蘊含的數學思想、方法充分挖掘.在此過程中，充分體現了數學知識的融會貫通，對數學學科核心素養的培養具有積極意義.