領略中考數學壓軸題的魅力,源于對題目的深入理解
——參加說題比賽所引發的思考
于川東 烏魯木齊市第七十中學 新疆烏魯木齊 830011
2018年,新疆烏魯木齊市教研中心舉行舉行了一次初中說題比賽,參賽教師根據比賽提供的歷年烏魯木齊市數學中考的壓軸題,需要按照“解法分析—題目立意—功能和價值—預測試題”的步驟撰寫課件.現結合說題比賽過程中的案例,談談自己參加這次比賽的一些思考.
一、試題的呈現
(1)求點C的坐標;
(2)設直線y=2x與拋物線交于A,B兩點(點A在點B的左側):
在拋物線的對稱軸上是否存在點G,使∠AGC=∠BGC?若存在,求出點G的坐標;若不存在,請說明理由;
(3)點P在直線y=2x上,點Q在拋物線上,當以點O,M,P,Q為頂點的四邊形是平行四邊形時,求點Q的坐標.
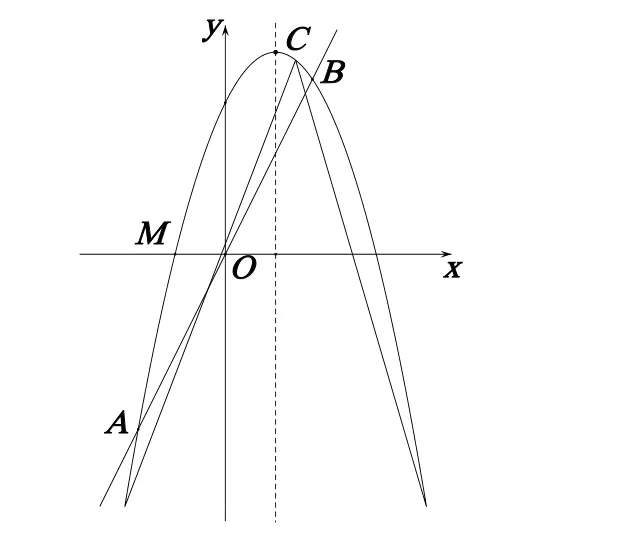
圖一
二、試題的解法分析
解:(1)由題意得- 1-2 + n= 0,解得 n=3, 得 C(1,4)
(2)存在符合條件的點G.
(方法1)求得交點A、B 坐標,再做點B關于對稱軸的對稱點B’,連接AB’交對稱軸于點G,連接BG,則∠AGC=∠BGC,設直線AB’解析式y=kx+b,解直線AB’解析式,最后得 G(1,6)
(方法2)過A、B兩點作對稱軸x=1的垂線AP和BQ,設G(1,a),
∵∠AGC=∠BGC,∠APG=∠BQG=90°,
解得a=6,得G(1,6)
【點評】這一問運用幾何畫板動態演示并度量出兩個角度的大小,能直觀的表達講解意圖.
(3)設 P(m,2m)
①當四邊形OMQP是平行四邊形時,
則 Q(m-1,2m),
∴ 2m=-(m-1)2+2(m-1)+3,
解得:m=0或2,
∴ Q1(-1,0)(舍),Q2(1,4),
②當四邊形OMPQ是平行四邊形,
③當OM是對角線時,分別過P、Q作x軸的垂線,垂足分別為G、H,可得△PGM≌△QHO,
∴ Q5(-1,0)(舍),Q6(1,4),
【點評】如果借助幾何畫板動態演示平行四邊形產生的過程,可以得到更富有啟發性的講解效果,提高解題效果.
三、題目立意和其他變式
第⑴問屬于基礎性的考查,來自九上二次函數第56頁第4題第(1)小題的變形.
第(2)問考查了化歸思想、數形結合思想、方程的思想。還可以進行以下變式:將問題∠AGC=∠BGC改為當△AGM周長最小時,求點G.
第(3)問考察平行四邊形存在問題,考查了分類討論、數形結合、方程與函數、化歸等思想.
四、本題功能和價值
試題突出考查了函數思想在幾何中的運用,涵蓋了方程、函數、平行四邊形等知識.試題在考查學生運算能力以及思維的靈活性、廣闊性方面具有較高的效度.
五、預測此類試題的趨勢和方向
1.基礎性:一定要注意核心概念、基礎知識,不脫離基礎.
2.綜合性:指代數、幾何等內容的基礎知識、基本思想方法的自然融合和聯系.
3.啟發性:對學生思維的啟發,能激發學生思維的創造力.
4.難度適中:不能任意的拔高難度.
說題比賽對于參賽教師各方面的能力要求很高.首先就解題能力而言,說題比賽要求提供盡可能多的解法和變式;其次說題比賽考察的是選手從多角度闡述一道試題的能力,這一點對教師的專業成長有極大的幫助;最后,說題比賽更關注參賽教師如何站在中考出題者的角度考慮試題的趨勢和方向,因此是一種更貼近教學實際的教研活動.

