基于中智模糊關聯規則生成的大數據挖掘分析算法

梁 凡 趙 麗

1(南寧職業技術學院信息工程學院 廣西 南寧 530008)2(山西大學軟件學院 山西 太原 030013)

0 引 言

隨著數據庫系統的大量建設與互聯網技術的廣泛應用，采用大數據挖掘技術對海量數據中蘊含的潛在價值進行分析逐步受到世界各國的高度重視，如商業、科技、健康、智能電網等[1]。大數據分析技術作為有效手段之一，可發現不同項目間潛在的未觀察到的關聯。關聯規則挖掘[2]作為大數據分析中的一類技術，指采用某種算法發現不同項目間可能存在的關聯或聯系[3]。例如，文獻[4]提出一種多尺度關聯規則挖掘算法，實現了多尺度數據集之間知識的跨尺度推導，算法具有較高的覆蓋率、精確度和較低的支持度估計誤差。文獻[5]針對動車組運維數據的數據量巨大、價值密度低的特點，提出了基于近似最小完美Hash函數的關聯規則挖掘算法，算例結果表明，挖掘出的規則可以有效地指導動車組修程修制優化，從而達到提高動車組運維效率的目的。類似研究見文獻[6-8]。但上述文獻均建立在經典的布爾型關聯規則基礎上，即輸出結果是0-1型的二進制數據。當應用經典的布爾型關聯規則進行數據庫定量分析時，會引入硬化數據“尖銳邊界”問題。換言之，經典布爾型關聯規則僅通過硬性的離散化劃分策略可能破壞了不同項數據間存在的內在聯系。針對傳統布爾型關聯規則挖掘算法存在的這一缺點，文獻[9]提出一種顧及模糊屬性的空間關聯規則挖掘方法，結合模糊集理論，采用隸屬度函數將模糊空間數據轉化為由隸屬度表征的模糊數值，進而將模糊空間屬性化為模糊集合，最終提取出模糊關聯規則。類似地，文獻[10]提出一種基于時間衰減模型的模糊會話關聯規則挖掘算法，同樣基于模糊理論進行關聯規則的模糊化挖掘。然而，現有的模糊關聯規則挖掘方法在量化語言學術語時過多依賴于人工或專家經驗進行劃分，很少考慮到規則本身存在的不確定性，故導致很難以最優方式生成關聯規則。

為解決現有關聯規則挖掘方法中存在的缺點，提出了一種新型的中智關聯規則挖掘算法，主要創新點為：

1) 針對傳統布爾型挖掘算法硬性關聯規則處理導致數據間聯系被破壞的風險，將模糊理論引入關聯規則挖掘模型中，從而提升數據間潛在聯系的挖掘成功率。

2) 針對傳統模糊關聯規則挖掘算法存在的語言學術語量化預處理過度依賴人工經驗的缺點，基于中智集合理論對傳統模糊關聯規則挖掘算法進行改進。不僅考慮了不同項間的隸屬度函數，并且綜合考慮關聯規則自身不確定性以及項間的非隸屬度函數，可更有效地實現關聯規則的模糊化處理并發現所有可能存在的關聯規則，有助于提升數據挖掘準確性。

1 關聯規則挖掘模型相關知識

為便于后續分析，首先給出關于關聯規則挖掘模型的基本術語與相關定義，隨后建立基于模糊化的關聯規則挖掘模型。

1.1 關聯規則挖掘模型

令集合|D|為從一個給定數據集中挖掘得到的關聯規則集合，相關定義如下：

1)I={i1,i2, …,im}表示所有可能的數據集合，其中元素稱為項目(item)。

2) 資料庫T表示來源于數據集I中進一步挖掘分析的數據集，滿足T?I。

3) 對于給定的項目集X?I以及一個給定的資料庫T，則T包含X當且僅當X?T。

4) 定義表示σX項集X的支持度(support frequency)，其含義為項集X在整個數據集中出現的頻率，公式如下：

(1)

5) 對于項集X、Y，X∩Y的可信度定義為同時包含X、Y的支持度與包含X的支持度之比：

(2)

6) 關聯規則：一個形如X?Y的蘊含式，其中X?I、Y?I且X∩Y=φ。關聯規則成立的條件是：① 資料庫T中至少有s%的項包含X∪Y，即具有最小支持度s；② 在資料庫T中包含X的項中最少有c%同時也包含Y，即具有最小可信度c。

關聯規則挖掘問題本質上就是確定不同項集見支持度和可信度分別大于用戶給定的最小支持度和最小可信度的關聯規則(即強規則)，具體包含以下兩個子問題：

子問題1：找出資料庫T中具有用戶定義的最小支持度的項目集，并將其定義為頻繁項目集，反之則成為非頻繁項目集。

子問題2：利用頻繁項目集生成關聯規則。

1.2 模糊關聯規則

關聯規則挖掘作為數據挖掘的主要任務，其生成的關聯規則表征了不同屬性的項集間的聯系。對于傳統布爾型關聯規則挖掘而言，其項目集的劃分往往采用精確截斷區間劃分的方式。但此種方法存在過于硬化處理的弊端，如10.1和9.9在事實上是兩個非常接近的數值，但在[1, 10)、[10, 20)的劃分方式下則會分屬于兩個不同的項目集合，顯然會導致與實際結果不符的情況。因此，模糊關聯規則進一步地運用模糊理論對關聯規則進行了改進，從而克服了傳統布爾型關聯規則生成算法對數據過于硬化的處理缺陷。

模糊關聯規則挖掘的基本原理為：設資料庫T={ti|i=1, 2, …,n}，項目集合I={i1,i2, …,im}，項目集合的每個元素ii對應一個模糊集合Lj={l1,l2, …,l|Lf|}(j=1, 2, …,m)。定義模糊項目集合為項目集合I中所有項目對應的模糊集所有成的集合，而模糊集的隸屬度函數可由專家進行人為定義，記為fjk，下標滿足：1≤j≤m，1≤k≤|Lf|，其實際意義為表征了項目元素ij隸屬于資料庫T的程度。例如，f12為項目i1所對應的模糊集合中第2個模糊項目的隸屬度函數。故根據給出的模糊集隸屬度函數，可將原資料庫集合轉換為模糊資料庫T={t′1,t′2,…,t′n}，且t′i= (f11,…,f1|L1|,…,fm1, …,fm|Lm|)，i={1, 2, …,n}。與傳統布爾型關聯規則相比，模糊關聯規則通過引入對數據的模糊化處理實現了劃分邊界的柔性過渡。

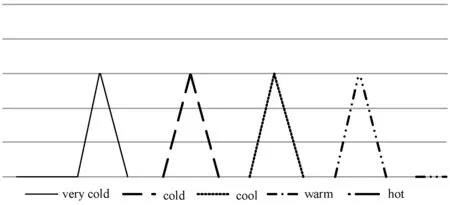
為更清晰地說明本文所提模糊關聯規則生成方法，本文以溫度相關的數據挖掘為例進行說明。在進行數據挖掘過程前，本文需對數據項進行預處理。其主要內容記為將語言學術語轉換為具有量化的數值，并定義每個語言學術語對應的量化數值范圍，此過程可基于專家知識進行。例如，表征溫度的語言學術語{very cold，cold，cool，warm，hot}。進一步地，不同的表征溫度的語言學術語的模糊化隸屬度函數可按如表1所示的數據資料庫進行計算，圖1為響應的隸屬度函數曲線。

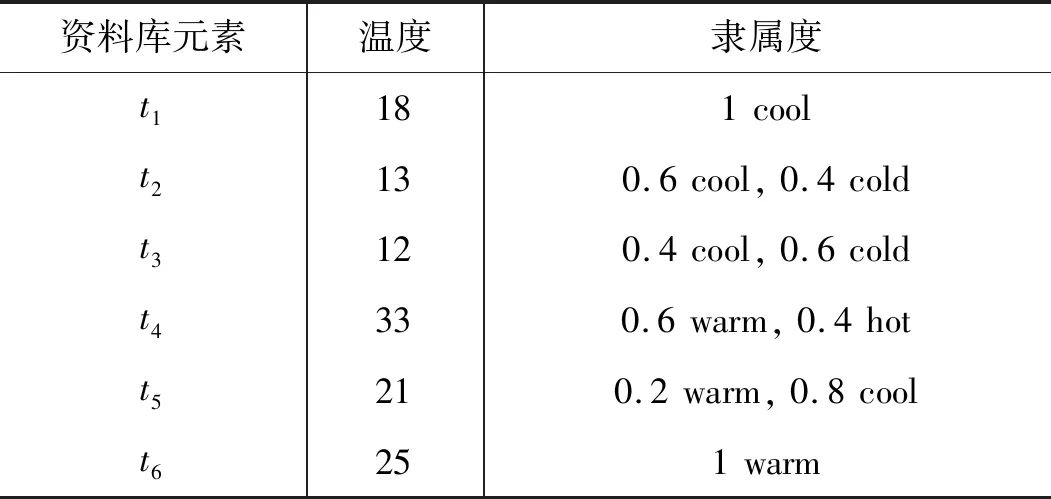
表1 數據庫事務的隸屬度函數

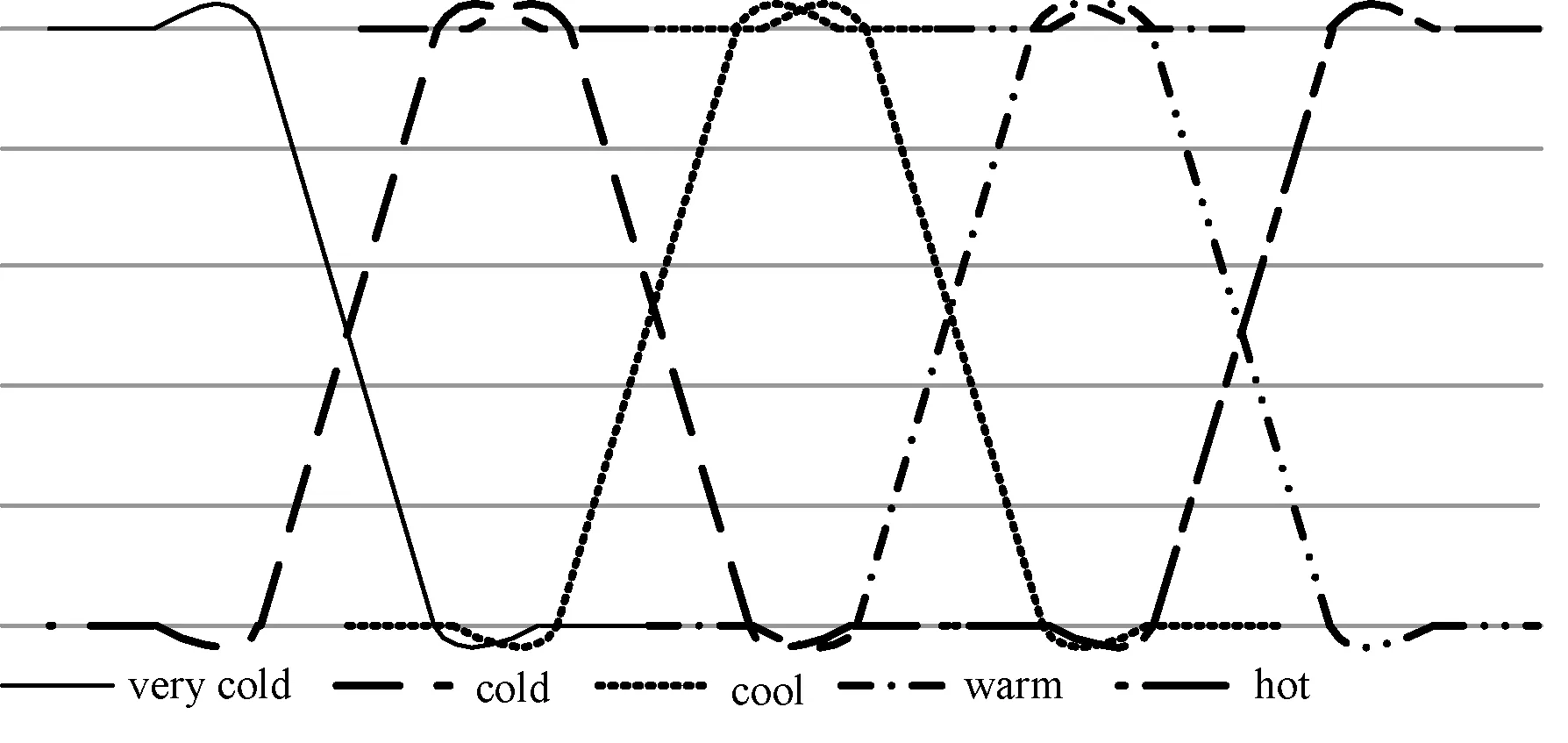
圖1 表征溫度的語言術語

將語言學術語{very cold，cold，cool，warm，hot}添加到候選集中，并計算這些項集的支持度，從而實現每個語言學術語的量化特征值，從而生成模糊候選集。依據2.1節中支持度的定義，本文可計算出單項集和多項集的支持度。同樣以溫度的單一指標和雙重指標為例，支持度如表2和表3所示。后續內容中，將包含k個項目的項集表示為k-項集，并記集合L中的k-項集為Lk。

表2 單一項集的支持度

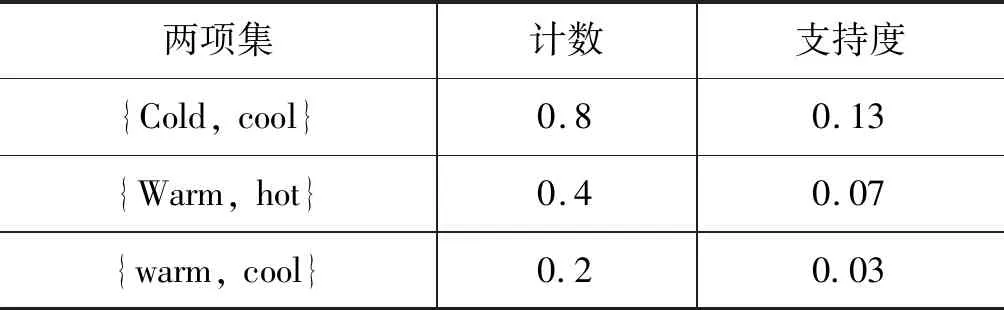
表3 兩項集的支持度

2 中智模糊化關聯規則挖掘模型

在經典的模糊關聯規則模型中，隸屬度函數的選擇仍存在過于依賴人工經驗的缺陷，即隸屬度函數同樣存在“硬化”的不足。此外，經典的模糊關聯規則模型并未考慮到數據集自身存在的不確定性。上述兩點將導致最后的挖掘結果可能因模糊隸屬度函數的選擇不同而出現偏差。中智學作為模糊理論的進一步發展，是模糊結合論、并行相容性集合論和直覺集合論的概括總結。因此，基于中智集合理論提出針對經典模糊關聯規則挖掘的改進算法，其進一步將數據元素的不確定性考慮在內，有效克服了傳統模糊理論的缺點。為此，首先給出中智集合的基本定理和運算規則，隨后進一步建立基于中智模糊的關聯規則挖掘模型[12-13]。

2.1 中智集合理論基本概念

中智集合理論中，設集合X為空間上的全集，而集合A是集合X的一個子集。而元素x∈X進一步表示為x(t,i,f)，其中t、i、f分別表示元素x的真實性、不確定性和非真實性概率，且有t=T(x)、i=I(x)、f=F(x)成立。T、I、F分別為元素x的真隸屬度、不確定性隸屬度和非隸屬度集合。根據文獻[11]定義，其為|-0, 1+|的標準和非標準實數子集，其中|-0, 1+|表示非標準單位區間，-0=0-ε，1+=1+ε，其中“0”、“1”表示集合邊界的標準值，而“ε”則表示不確定度(即非標準部分)且為無窮小正數。故T、I、F的上確界和下確界以及對應的模糊集合的上確界和下確界分別表示為：

SupT=tsupInfT=tinf

(3)

SupI=isupInfI=Iinf

(4)

SupF=fsupInfF=finf

(5)

nsup=tsup+isup+fsup

(6)

ninf=tinf+iinf+finf

(7)

-0≤SupT+SupI+SupF≤3+

(8)

進一步，文獻[14]定義了單值中智集合的概念，以克服經典中智集合理論中對真隸屬度、不確定性隸屬度和非隸屬度集合定義過于抽象不適合應用于實際工程中的缺陷。設X為論域，而集合X上的單值中智集合A具有如下形式：

A={:x∈X}

(9)

式中：TA(x):X→[0,1]，IA(x):X→[0,1]，FA(x):X→[0,1]，從而對于所有x∈X，都有0≤TA(x)+IA(x)+FA(x)≤3 。區間TA(x)、IA(x)和FA(x)分別表示單值真隸屬度、不確定隸屬度和假隸屬度函數。進一步將式(9)簡記為A=(a,b,c)，其中a,b,c∈[0, 1]，且有a+b+c≤3。

2.2 中智集合的基本運算

1) 交集運算：對兩個單值中智集合A=和B=，其并集操作定義為C=A∩B，C的真隸屬度函數、不確定隸屬度函數和假隸屬度函數分別定義為TC(x)=min(TA(x),TB(x))、IC(x)=min(IA(x),IB(x))和FC(x)=max(FA(x),FB(x))。

2) 并集運算：對兩個單值中智集合A=和B=，其并集操作定義為C=A∪B，C的真隸屬度函數、不確定隸屬度函數和假隸屬度函數分別定義為TC(x)=max(TA(x),TB(x))、IC(x)=max(IA(x),IB(x))和FC(x)=min(FA(x),FB(x))。

3) 包含運算：中智集合A包含于另一個中智集合B，可表示為A?B，當且僅當對于所有x∈X，有TA(x)≤TB(x) 、IA(x)≤IB(x)且FA(x)≥FB(x)。

2.3 中智模糊化關聯規則模型

提出的基于中智模糊化關聯規則生成模型為：X→Y，其中X∩Y=?，X、Y均為中智集合。本文目標為找到頻繁集和相應的支持度，以及其相應的關聯規則生成準則。結合2.2節中的模糊化關聯規則定義，本文將中智集合添加到集合I中，集合I為所有可能的數據集(即項集)。具體操作為I=N∪M，其中N是中智集，M是經典項集。關聯規則的一般形式為：

X→YX?I，Y?I，X∩Y=?

上述中智模糊關聯規則生成流程如圖2所示。

圖2 中智模糊關聯規則生成流程

同樣以溫度相關的關聯規則挖掘為例說明本文的中智模糊關聯規則建模流程。

Step1設置溫度相關的語言學術語{very cold，cold，cool，warm，hot}的量化數值范圍如表4所示。

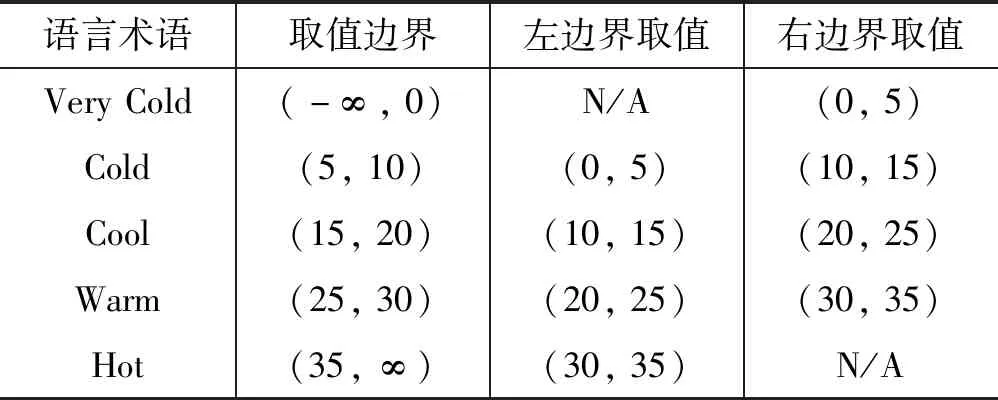
表4 語言術語的量化數值范圍

Step2基于表4中量化的語言術語范圍，定義溫度的真隸屬度、不確定隸屬度和非隸屬度函數。式(10)-式(14)為真隸屬度函數，式(15)-式(19)為不確定隸屬度函數，式(20)-式(24)為非隸屬度函數。

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

圖3為這些變量的真隸屬度、不確定隸屬度、非隸屬度函數以及中智模糊化隸屬度函數。

(a) 真隸屬度函數

(b) 不確定隸屬度函數

(c) 非隸屬度函數

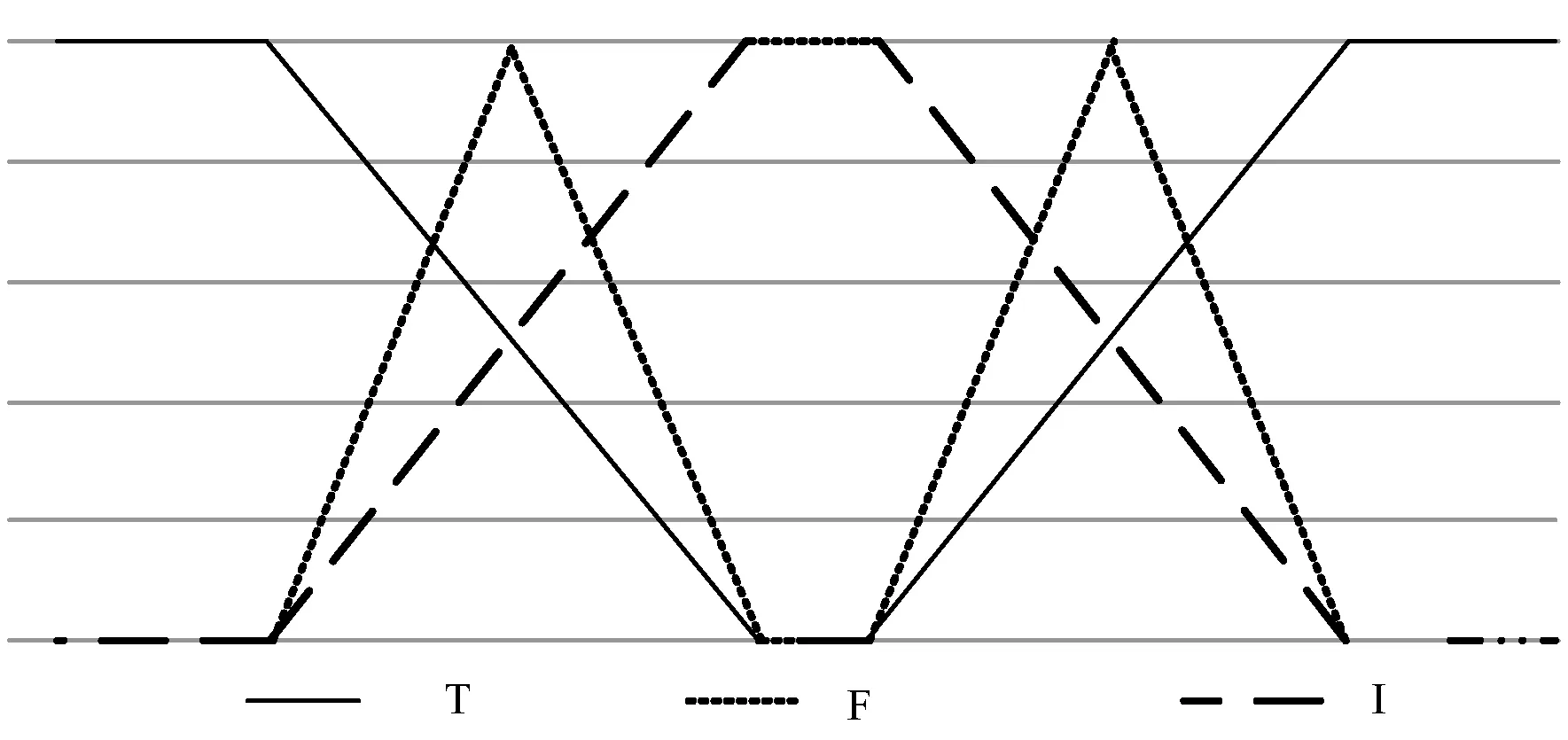
(d) 中智模糊化隸屬度函數圖3 隸屬度函數波形

Step3基于隸屬度函數數值，不同的項集被劃分至不同的溫度集合中，如表5所示。

表5 不同數據庫事務的隸屬度函數

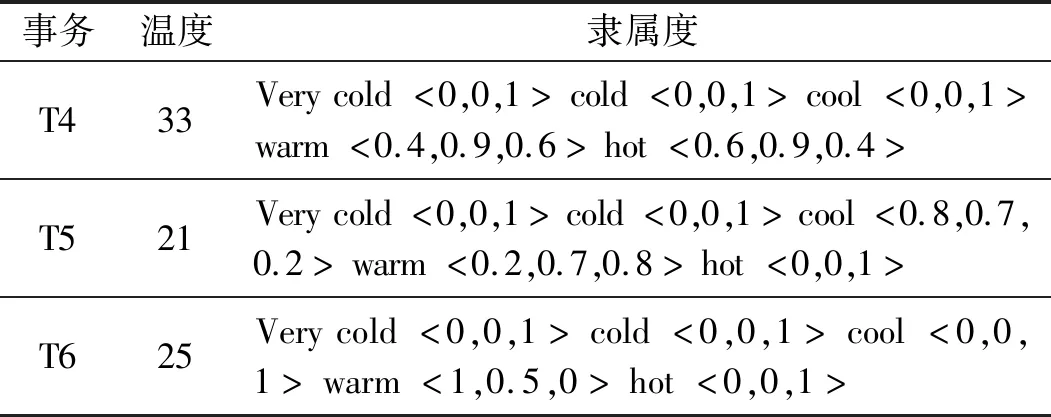
續表5

Step4計算資料庫中每個元素的語言學術語集合{very cold, cold, cool, warm, hot}。由于真隸屬度、假隸屬度和不確定隸屬度是獨立的函數，所以語言學術語的集合可以擴展到{Tvery-cold,Tcold,Tcool,Twarm,Thot,Fvery-cold,Fcold,Fcool,Fwarm,Fhot,Ivery-cold,Icold,Icool,Iwarm,Ihot}。其中，Fwarm表示不溫暖，而Iwarm表示不確定是否溫暖。

Step5使用表5中給出的隸屬度函數，分別計算單項集和兩項集的頻數和支持度，如表6、表7所示。

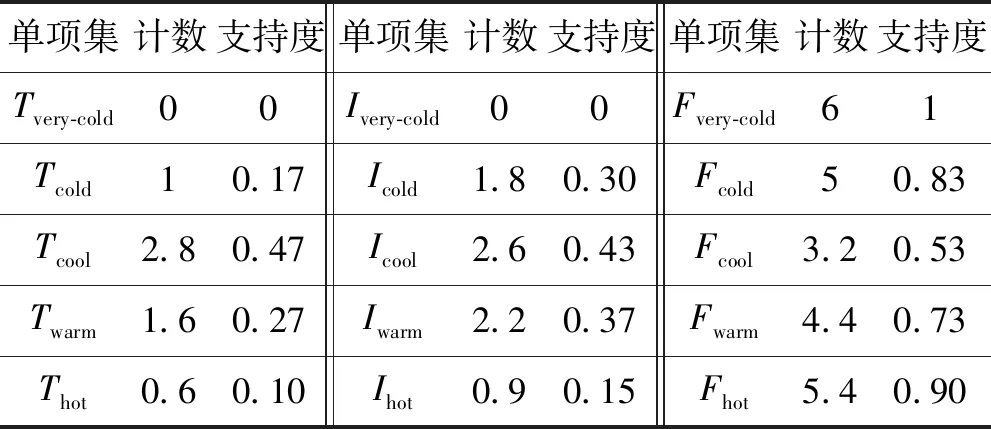
表6 單項集中智集的支持度

續表7

3 實 驗

為說明所提方法的實際運行效果，在同樣的實驗條件下(計算機配置為Intel Core i5 CPU, 10 GB RAM, Windows 10 64位 旗艦版)，并將其與文獻[15]所提布爾型關聯規則挖掘算法以及文獻[16]所提傳統模糊關聯規則挖掘算法進行對比。實驗程序統一采用VB.net進行編程。

3.1 實驗數據預處理

股票交易市場的歷史數據來源于2012年9月至2017年9月期間埃及股票市場。數據包含每只股票的開盤價、收盤價、最高價、最低價和成交量。本文以開盤價(openprice)與收盤價(closeprice)的差值比率定義股票的變化率(pricechangerate)：

(25)

并定義股票成交比例如下：

(26)

此外，數據屬性項包含季度、月度、股票變化率、成交率、指標變化率，表8表示了預處理后的部分數據。

表8 預處理后部分數據

根據上述語言學術語，基于單值中智集合定義對上述數據進行模糊化處理。本文將變化率模糊化處理為{“high up”，“high low”，“no change”，“low down”，“high down “}，而對于成交量，模糊化處理為{“low”, “medium”, “high”}，其對應的隸屬度函數波形分別如圖3、圖4所示。

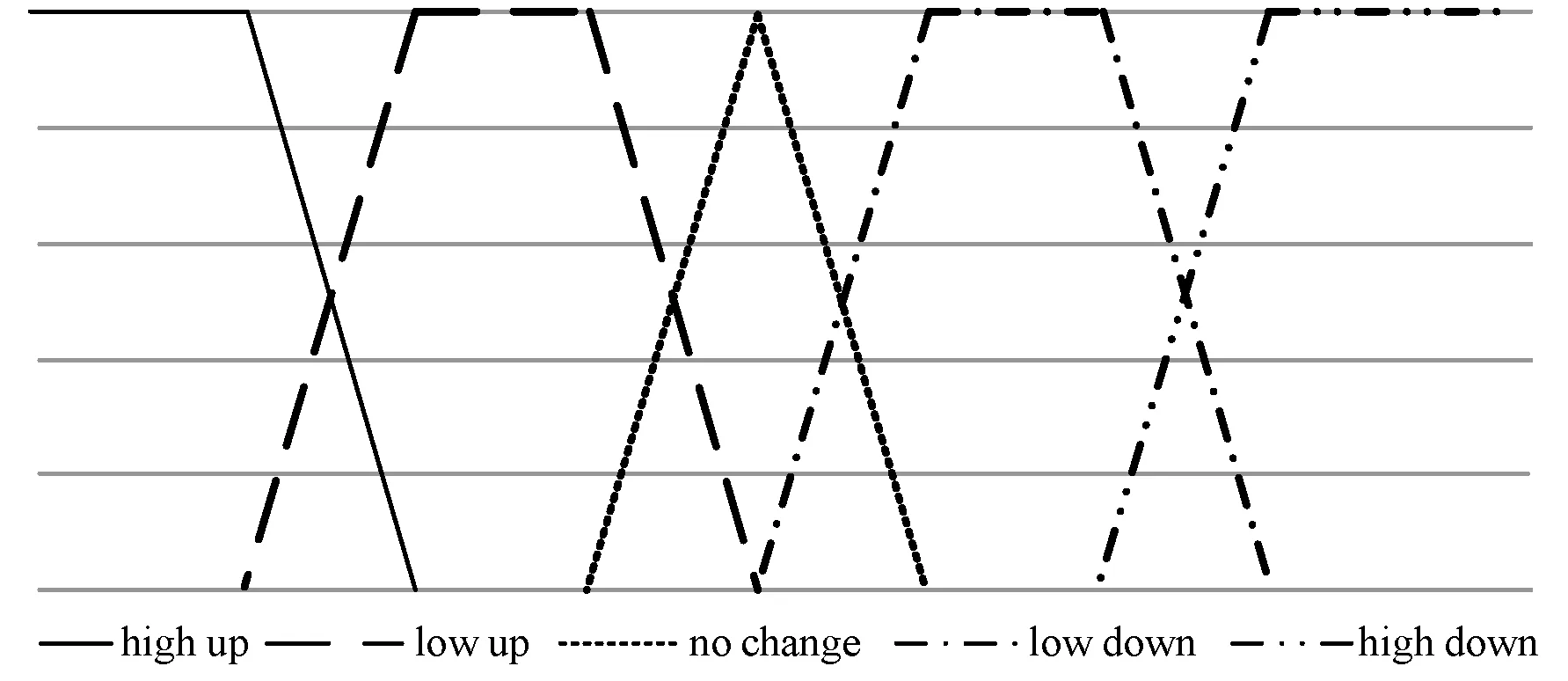
圖3 變化率真隸屬度函數

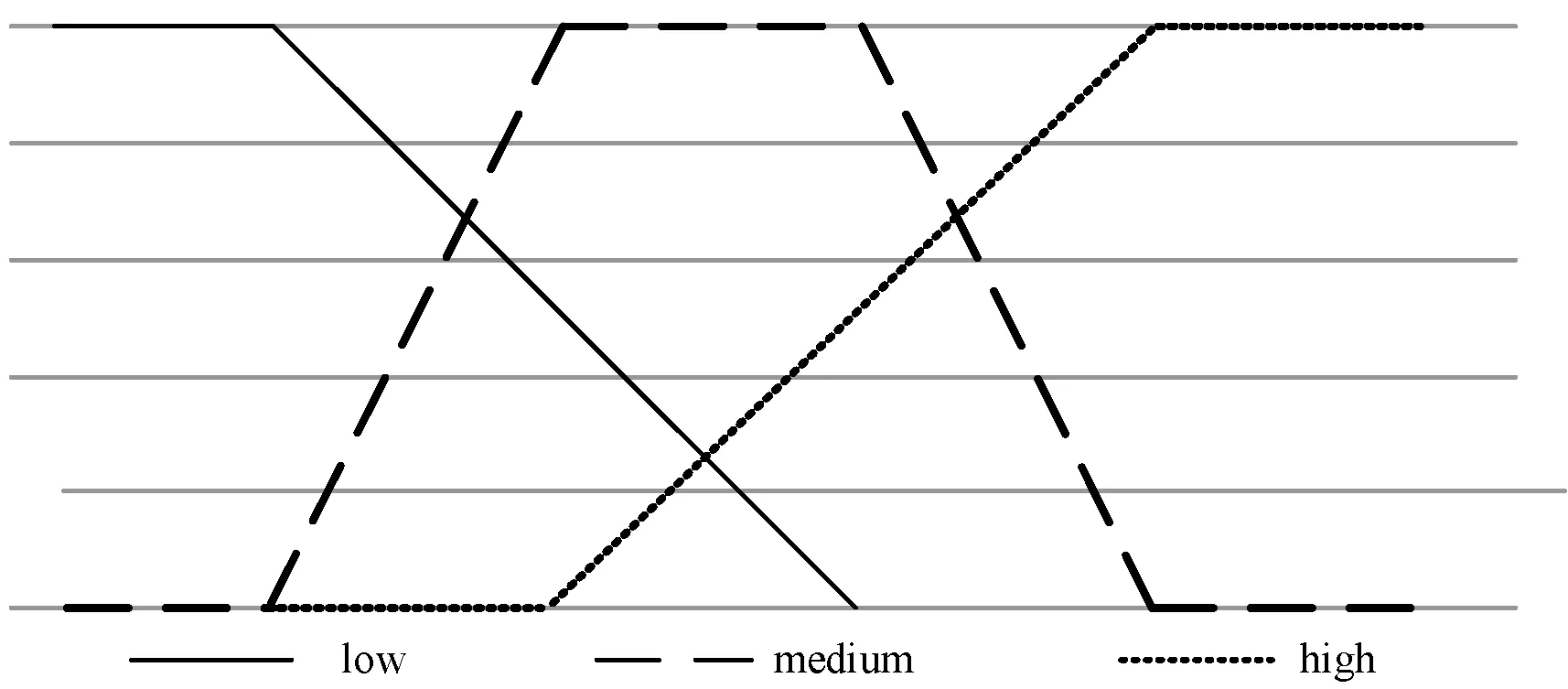
圖4 成交量的真隸屬度函數

3.2 實驗結果

3.2.1生成關聯項數量分析

基準實驗中，設最小支持度為0.02，對比分析不同關聯規則挖掘方法下生成的關聯項數量。如表9所示，由于所提中智模糊化算法考慮了不確定性和非隸屬度函數，故在關聯項的數量上，應用所提中智模糊關聯規則生成的關聯項較布爾型算法布爾型算法提升了270%，而較文獻[16]提出的傳統模糊算法提升了142.9%。由此可見，本文方法能夠顯著挖掘出更多的潛在關聯規則。

表9 關聯項生成數量

3.2.2最小支持度對關聯規則生成數量的影響

本節研究了最小支持度對不同挖掘算法所生成的關聯規則的影響。圖5、圖6和圖7分別為文獻[15]提出的布爾型關聯挖掘算法、文獻[16]提出的模糊關聯挖掘算法和本文所提中智模糊關聯規則挖掘算法所生成的關聯規則數量隨項集數量的變化趨勢。橫向比較圖5-圖7，可發現隨著最小值尺度閾值的升高，關聯規則生成數量均處于下降狀態，且隨著項目集合的增多，二者下降速率均逐漸加快。而縱向比較可知，當最小支持度閾值設置較小且項目集合數量較低時，中智模糊關聯規則挖掘算法的性能與文獻[16]提出的模糊關聯規則生成算法的性能相近，而文獻[15]提出的布爾型挖掘算法由于生成關聯數量較少，性能則較差。但當項目集合增多時，由于中智集合考慮了更多的隸屬度函數，使得挖掘到的關聯規則數量遠大于文獻[16]提出的模糊關聯規則挖掘算法。

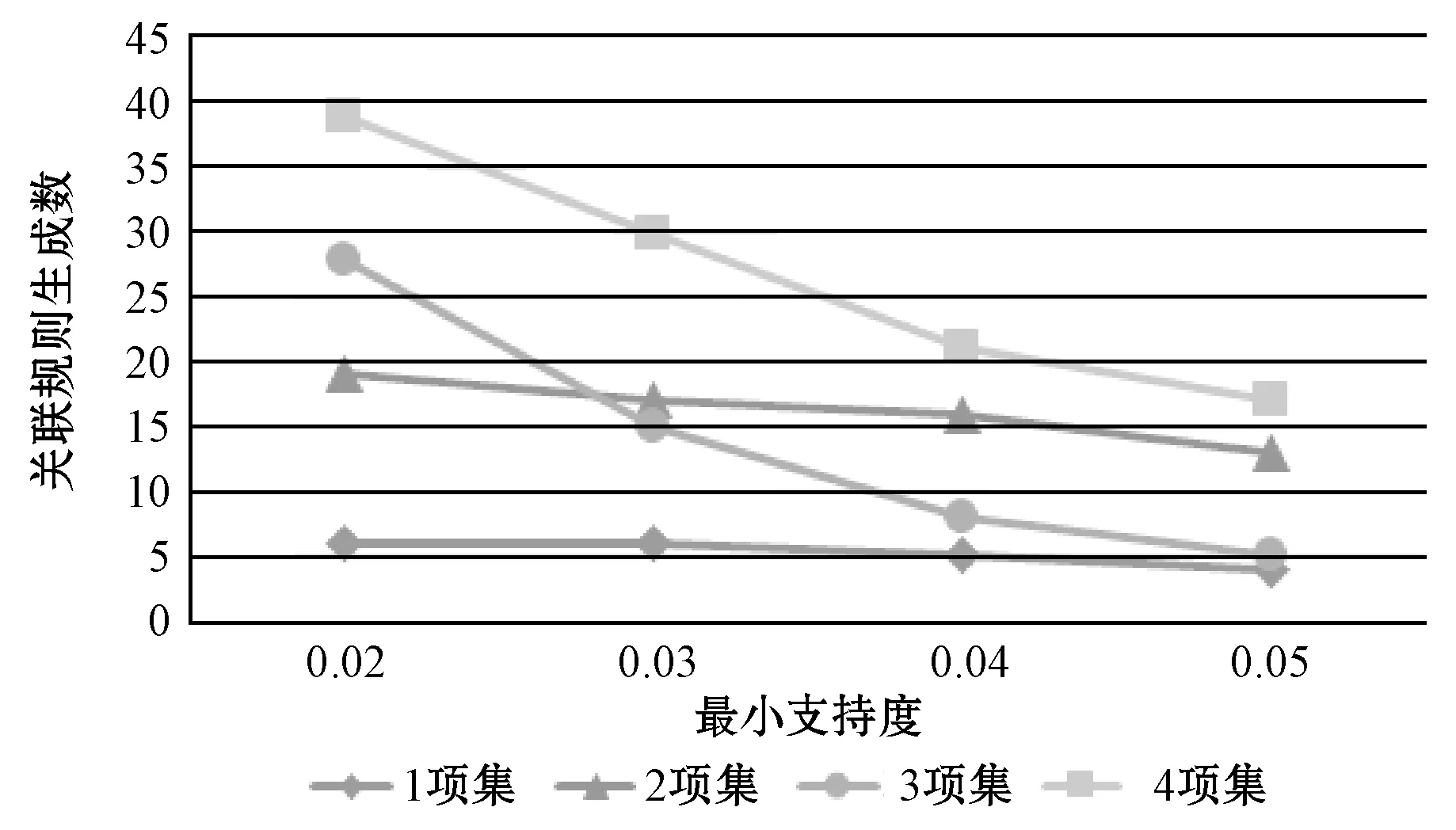
圖5 文獻[15]提出的布爾型關聯規則生成數量隨項集數量變化趨勢

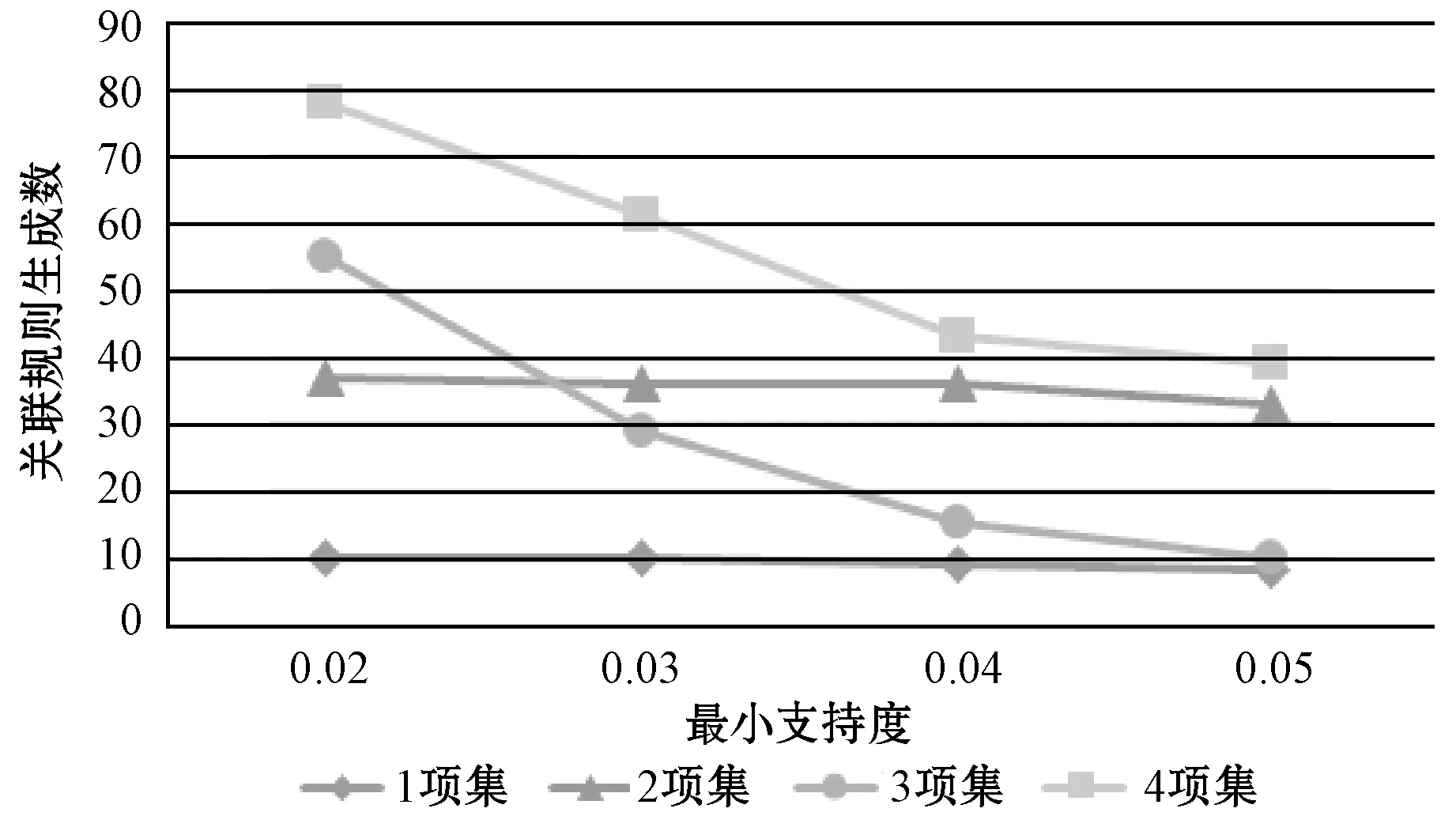
圖6 文獻[16]提出的模糊關聯規則生成數量隨項集數量變化趨勢

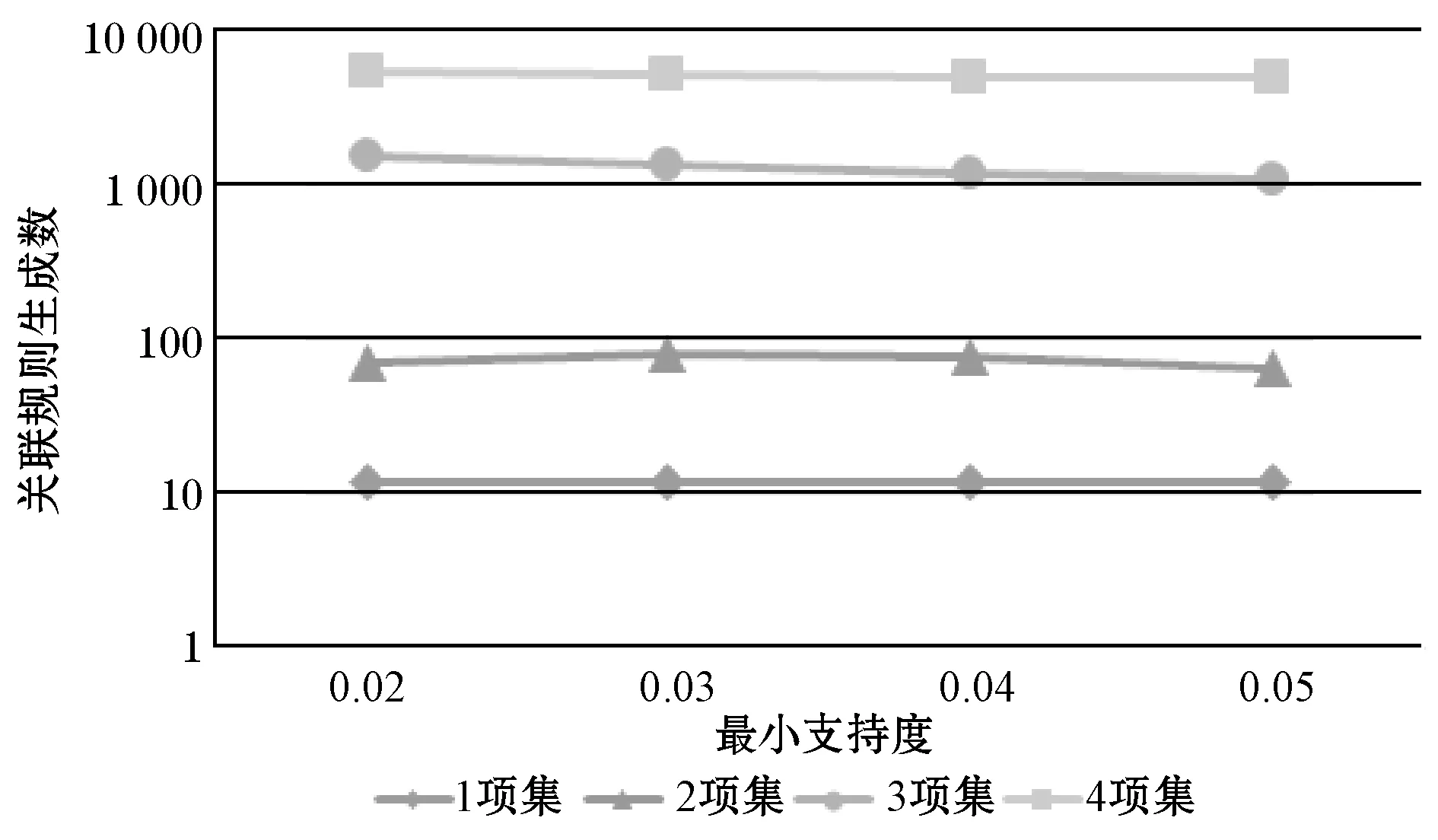
圖7 中智模糊化關聯規則生成數量隨項集數量變化趨勢

然而，中智模糊化方法雖然顯著增大了關聯規則數量，但過多的關聯規則數量可能給用戶帶來信息誤導的風險。因此，本文進一步研究最小支持度對本文所提中智模糊關聯規則挖掘算法的性能算法。圖8為最小支持度閾值從0.5到0.9變化時采用中智模糊關聯規則生成算法所產生的關聯規則數量與支持度和項集數量的變化趨勢。

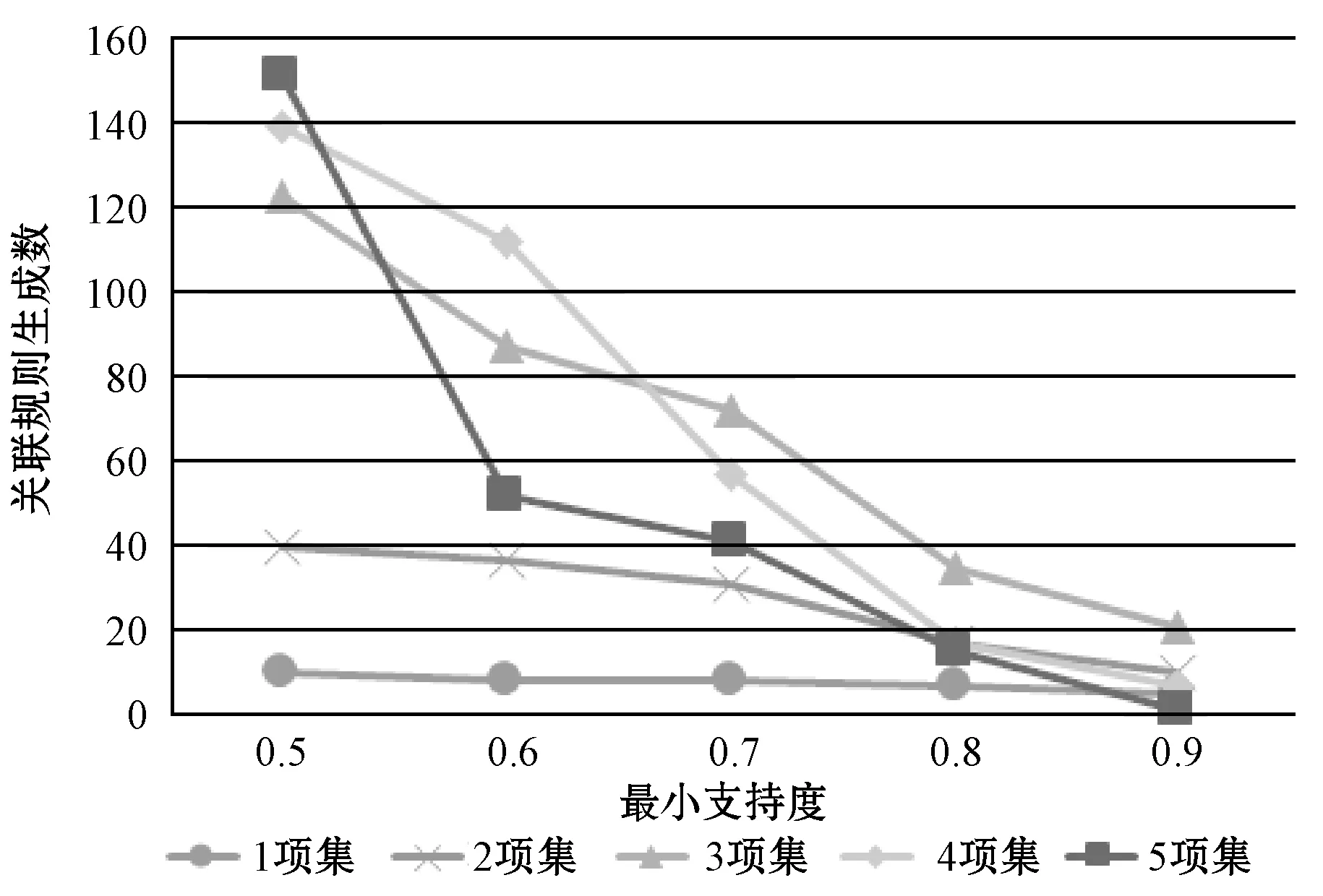
圖8 中智規則數量隨最小支持度變化關系

對比圖7和圖8可知，當采用本文所提中智模糊關聯挖掘算法時，最小支持度大于50%時能夠有效濾除過多生成的關聯規則，得到和傳統模糊關聯規則挖掘算法相近的性能。

綜上可得：1) 本文算法能夠得到用戶感興趣的強關聯、有價值的數據信息；2) 本文算法在挖掘得到的關聯規則上的可信度要強于其他兩種對比算法；3) 在算法中考慮更多的隸屬度函數，有助于增加挖掘到的關聯規則數量。

4 結 語

針對傳統布爾型關聯規則挖掘算法存在的硬化數據“尖銳邊界”問題以及傳統模糊關聯規則挖掘算法未考慮關聯規則的不確定性與非真實性問題，提出一種新型中智關聯規則挖掘算法。通過實例分析表明，相比其他兩種對比算法，本文算法在相同支持度時能夠挖掘更多數量的關聯規則，在多項集關聯規則生成數量與可信度上具有明顯優勢，有助于提高數據挖掘的準確性。此外，算法考慮了更多的隸屬度函數，有助于增加挖掘到的關聯規則數量。后續研究工作中，將繼續深入研究模糊邊界設定值對生成關聯規則數量的影響以及算法普適性研究。