兩個無證書代理環簽名方案的攻擊與改進

李慧敏 寧華英 梁紅梅 張金輝

1(莆田學院數學與金融學院 福建 莆田 351100)2(閩南師范大學數學與統計學院 福建 漳州 363000)3(應用數學福建省高校重點實驗室 福建 莆田 351100)

0 引 言

隨著計算機網絡和電子商務的的快速發展，數字簽名的應用越來越廣泛。例如：代理簽名[1-2]讓人們能夠通過代理人進行一些簽名操作，在電子認證方面起著重要的作用；環簽名[3]讓人們能夠在不泄露自己身份的情況下完成簽名，它是由Rivest等[3]在研究如何匿名泄秘的現實背景下首次提出的一種新型無條件匿名簽名，在電子商務、匿名通信及區塊鏈等方面中都有廣泛的應用[4-5]。在某些特定場合，代理簽名人更傾向以完全匿名的方式進行代理簽名，因為他們認為這種方式能更有效地隱藏自己的身份不讓任何人(包括他的原始簽名人)得知，從而能更好地保護好原始簽名人及代理簽名人的隱私，如代理環簽名[6]、代理群簽名[7]或盲環簽名[8]均可實現這個目的。而在代理環簽名[6]中，環中任意一個成員都可以代表其他環成員進行代理簽名而不被他人得知，而且沒有人能判斷出誰是真正的簽名實施人，這樣可以很好地保護代理簽名人。因此，代理環簽名因既能滿足原始簽名人的委托簽名權力，又能保護代理人的隱私而受到眾多學者的青睞。基于身份的代理環簽名[9-11]、基于證書的代理環簽名[12-13]和無證書的代理環簽名方案[13-19]不斷被提出，其中無證書公鑰密碼系統避免了密鑰生成中心(Key Generating Center,KGC)失信問題，同時也不需要認證中心頒發、驗證、保管證書，可以滿足代理環簽名的可區分性、不可偽造性等基本性質。文獻[19]提出了一種采用短簽名方案進行授權的無證書的代理環簽名方案，該簽名方案是基于文獻[20]中所提出的一種無證書環簽名方案而設計出來的。遺憾的是，我們分析發現該簽名方案是不安全的，原始簽名人的私鑰可被恢復出來。另外，標準模式下的簽名方案與隨機預言模型相比不需要完全隨機的Hash函數，而是依賴于一些不可逆的單向的或在現實生活中能夠實現的Hash函數，它也是基于一些困難問題假設[21]。因此，標準模型下的安全性證明是一種符合現實并讓人信任的證明方式。張春生等[22]提出了一個標準模型下的無證書代理環簽名方案，該簽名方案是基于CDH(Computational Diffie-Hellman)問題假設，只需要兩次對運算。然而，我們從該方案的驗證式中發現該方案不具備不可否認性，任何人都可以偽造簽名。本文指出了文獻[19]和文獻[22]中兩個方案的安全問題，并給出了具體的攻擊方法，最后給出了相應問題的改進方法，對構造安全的無證書代理環簽名方案具有重要的借鑒意義。

1 預備知識

1.1 雙線性對的定義

假設存在兩個循環群G1和G2，它們的階數均為素數q，且G1為加法群，G2為乘法群。設P為G1的生成元。假設映射e:G1×G1→G2是一個雙線性對，那么G1、G2滿足如下性質：

(1) 非退化性：e(P,P)≠1；

(2) 可計算性：存在一個有效的算法計算e(P,Q)，其中P,Q∈G1；

1.2 困難性問題

在數據規模達到一定的情況下，下面兩個問題是困難的。

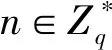
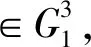
1.3 代理環簽名方案的構造及安全性需求

代理環簽名方案一般由四個步驟組成，即系統參數設置(產生授權人和代理人密鑰對及相關系統參數)、代理密鑰產生(生成代理簽名密鑰對)、簽名生成(輸入待簽名的消息、相關系統參數、身份信息的集合和代理人的代理簽名私鑰后得到該消息的簽名)和簽名驗證(確定簽名是否有效)。安全性需求包括以下四點：

(1) 可驗證性 所有人都可以去驗證簽名方案的正確性。

(2) 無條件匿名性 真正的代理簽名人不會被原始簽名人和包括KGC在內的第三方得知。

(3) 不可偽造性 只有被授權的代理簽名人才可以計算出有效的代理環簽名。而沒有被授權的任何人(包括原始簽名人和KGC)都無法偽造出有效的代理環簽名。

(4) 可區分性 代理環簽名可以與代理人用自己的私鑰產生的環簽名區分開來。

2 文獻[19]簽名方案的分析

2.1 方案回顧

為了達到構造簡潔、并提高授權期間的傳輸效率，文獻[19]中的無證書代理環簽名方案在授權時使用雙線性對構造一種短簽名方案。具體方案如下：

設授權人為A，代理人為B，B建立一個包括他自己在其中的環u={U1,U2,…,Un}，待簽名的消息為m，A對B的授權信息表示為w。

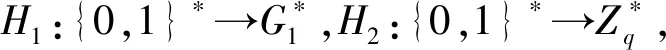
用戶密鑰生成：

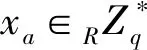
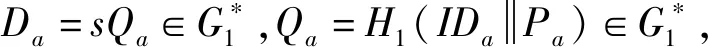
(3)A生成自己的私鑰Sa=xaDa=xasQa。

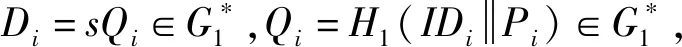
代理密鑰生成：

(1)A創立一個只有簽名人才可認證許可的信息w，其中信息分別包括A和B的身份信息、說明授權關系以及使用限制等。隨后進行計算Sw=H2(w)Sa,然后將(Sw,w)傳送給B。

(2)B驗證e(Xa,P0)=e(Ya,P)以確認授權人的身份，然后驗證e(Sw,P)=e(Qa,Ya)H2(w)是否成立。如果該驗證成立，則表示授權步驟已完成。

代理簽名：

(1)B選擇包括自己本身在內的n個用戶來成立一個環u={U1,U2，…,Un},L={P1,P2，…,Pn}為環用戶的公鑰集，已知B為Ub,1≤b≤n。

(3) 隨機選擇A∈G1。

(5) 計算hp=H2(u,m,Rb)。

(7) 消息m的簽名為：

Sign=(u,m,R1,…RR,hτ,…,hη,σ,H2(w))

簽名驗證：

(1) 驗證下列各式：

e(Xa,P0)=e(Ya,P),e(Xi,P0)=e(Yi,P),hi=H2(u,m,Ri),i=1,2，…,n；

(2) 驗證下式：

若上述等式都成立，則接受簽名。

2.2 安全性問題

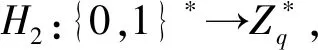
(H2(w))-1Sw=(H2(w))-1H2(w)Sa=Sa

由此可以看出代理簽名人B可以通過A傳遞給B的(Sw,w)恢復出原始簽名人A的私鑰。所以該簽名方案是不安全的，會受到恢復密鑰的攻擊。因此，要克服該攻擊就要重新設計新的代理密鑰的產生方式，從而需要重新設計相應的簽名方案。但是，這里存在的安全問題在沒有注意運算性質的情況下容易被忽視。

3 文獻[22]簽名方案的分析

3.1 方案回顧

文獻[22]所提出的標準模型下的無證書代理環簽名方案是由系統參數設置、用戶密鑰產生、代理密鑰生成、代理環簽名算法和驗證算法構成，具體方案如下：

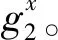
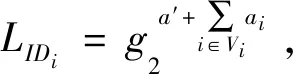
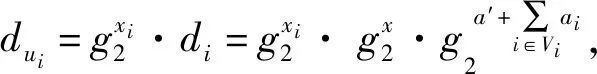
代理密鑰生成：授權人AI將授權信息ω、消息集mω及代理成員集合L={u1,u2,…,un}發送給KGC，其中，ω包含了AI的身份信息以及AI與L的授權管理。

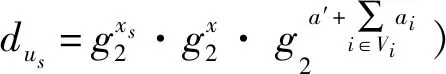
若上式成立，則(t,dAI)是合法有效的授權簽名信息，us驗證后計算得到自己的代理簽名密鑰dSAI，且dSAI=dus·dAI。

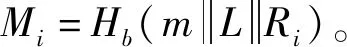
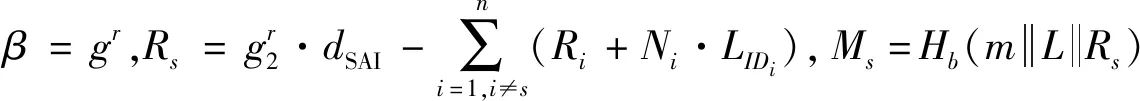
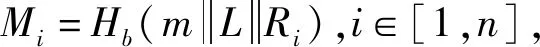
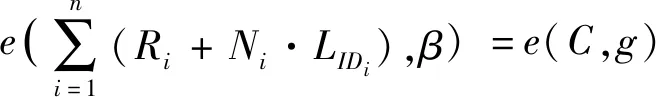
3.2 攻擊方案

經過分析，我們發現張春生等[22]所提出的上述標準模型下的無證書代理環簽名方案在面對惡意用戶攻擊時，將不再滿足不可偽造性這一安全特性，下面將給出具體的攻擊方法：

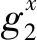
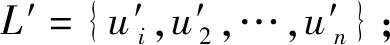
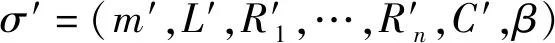
e(C′,g))

則該簽名有效。至此，惡意用戶成功地創建出有關m′的簽名σ′。

3.3 安全性分析與改進

(1) 用戶的私鑰生成方式是有問題的：原方案中把系統主密鑰乘以一個用戶也可以生成的數據作為用戶的部分私鑰，這樣導致了系統主密鑰可被用戶恢復出來。因此，要克服這個問題，就得改變用戶部分私鑰的生成方式，不能直接用相乘的方式來產生。

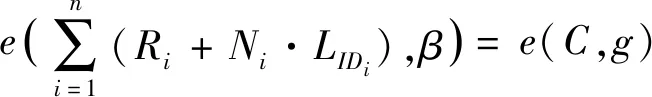
4 結 語

代理環簽名使得原始簽名人既可以委托別人代替自己簽名，又可以保護自己的匿名性。因此，代理環簽名在對用戶身份等隱私信息的保護具有較高要求的領域(如電子現金、電子投票、電子選舉、匿名通信等)具有廣泛的應用價值。標準模型下簽名方案的安全性證明更貼近實際并且更具有說服力，近年來逐漸成為關于簽名方案研究的熱點問題。現有的無證書代理環簽名及標準型模型下可證明安全的無證書代理環簽名方案的研究文章還不是很多，而且現有的很多方案存在可被偽造等不安全的問題。本文對文獻[19]所發表的無證書代理環簽名方案以及文獻[22]中的標準模型下的無證書代理環簽名方案進行安全性分析，發現這兩個方案均存在一定的安全性漏洞，容易被惡意用戶的攻擊，如惡意用戶可以恢復出KGC保管的系統主密鑰，從而對代理環簽名成功進行偽造。最后，本文給出的分析方法對同類代理環簽名方案的設計具有借鑒參考意義且具有部分的使用價值。