論蒙提霍爾悖論中的信息不對稱

許萬承

摘 要：蒙提霍爾悖論自被提出至今已有近五十年的歷史，由于其簡單易懂卻又違反日常直覺的特性，長期受到學界內外廣泛討論。然而學者們普遍關注該悖論的形成機制以及解悖方案，而對該悖論所顯露的信息不對稱問題有所忽視。故本文將對蒙提霍爾悖論予以介紹，揭露該悖論中存在的信息不對稱在問題，并借此對經濟學中的理性人假設做出要批判。

關鍵詞：蒙提霍爾悖論 理性人假設 信息不對稱

一、蒙提霍爾悖論的來源

蒙提霍爾悖論又稱三門悖論，最初來源于美國一個廣受歡迎的電視節目“讓我們來做交易”。該節目要求參與者從三扇關閉的門中做出選擇，三扇門中有兩扇后面藏著山羊，一扇則藏著汽車。如果參與者選中了藏著汽車的那扇門，那么他將會獲得獎品，沒有選中就會被宣告失敗。為了使節目更一波三折，在參與者選定一扇門之后，主持人蒙提·霍爾并不急于宣布結果，而是會打開沒有被選擇的兩扇門中的一扇，由于主持人知道每扇門后面的情況，所以可以保證打開的門后面藏著的是山羊。然后再詢問參與者，是否要變更自己的選擇：堅持原來選定的門，還是改換成剩下那個沒被選擇的門。

原本這個節目雖受歡迎，卻并沒有形成對參與者是否應該換門這一行為策略的嚴肅思考，直到有好事者給號稱“最聰明的女人”的專欄作家瑪麗蓮投稿，詢問參與者的最佳決策。瑪麗蓮回復的是應該選擇換門，這樣獲勝的概率將會是不換門的兩倍，也就是說換門的取勝概率為2/3，不換門則為1/3。該回復引發了軒然大波，瑪麗蓮收到了大量的讀者來信，批評她的回復是錯誤的，其中還有聲稱自己是已獲得數學或者統計學博士學位的專家學者。顯然大部分的批評者都有這樣的直覺，無論換不換門，獲勝的概率都應當是均等的1/2，然而事實證明瑪麗蓮是對的。經過對該節目的大量統計分析，結果發現選擇換門的獲勝概率確實近似是不換門的兩倍。

二、基于概率表的解答方案

蒙提霍爾悖論形式結構的簡單性和其違反直覺的深刻性形成了鮮明的比照。疑問也隨之而來，既然瑪麗蓮的答案是正確的，那么為什么大多數人卻會弄錯呢？對于大多數人而言，換不換門獲勝概率都應該是1/2，這才符合大眾的日常直覺。

大多數認為概率是1/2的人實際上是將節目的競猜模式混淆為這樣一個情況：參與者在選擇之前，主持人直接為參與者排除了一個錯誤選項，參與者在剩下的兩個門做出選擇。在這種情況下，主持人排除某一錯誤選項的行為是先于參與者的選擇行為的。參與者也就從三選一轉變為二選一，獲勝概率自然就是1/2。

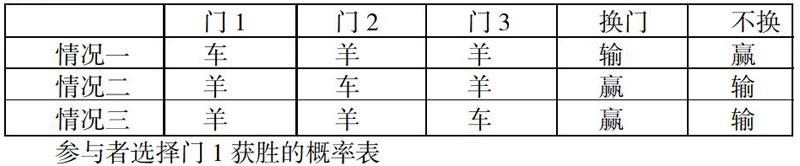
然而實際上節目的運作模式是參與者選定了一扇門之后，主持人再排除另外一扇沒有獎品的門，這時候概率就大不相同了。為了便于理解，可以畫出以下的獲勝概率表格。該表假定參與者選定的就是門1，各行表示獎品實際分布的三種可能情況，而這三種情況出現的概率是均等的，都是1/3。

有必要對該表格給出說明，首先表格雖然假定參與者選定門1，但是無論參與者選擇哪個門，實際的獎品分布也僅是表格中顯示的三種可能的情況，獲勝概率自然也是相同的;其次在表格里，并沒有表明主持人打開的是哪扇門，因為這是沒有必要的，我們可以推知在不同情況下，主持人開的是哪扇門：第一種情況中，參與者已經選對了，主持人開門2或者門3都沒有區別，所以他會隨機開門2或者門3。而在第二種情況和第三種情況中，參與者一開始就選擇了一個錯誤的門，主持人為了避免打開有獎品的門，只能打開另外一扇沒有獎品的門。現在可以從表格看出來，換門的獲勝概率是2/3，不換門則為1/3。瑪麗蓮也正是憑此方法得到了正確的答案。

該表格雖然給出了一定的解釋，然而依舊不足以打消大多數人的疑惑。雖然獲勝概率在表格中清晰地體現出來，但是日常的直覺總還是會告訴我們，主持人打開一扇沒有獎品的門之后，獎品要么在參與者選定的門里，要么在剩下的沒選的門里，所以概率好像應該是均等的。由此可見該方案雖然有效，但是解釋力終歸是有限的。

三、蒙提霍爾悖論中的信息不對稱

蒙提霍爾悖論的關鍵之處在于主持人是在參與者選定之后再進行對游戲的干預，而干預行動的前提就是主持人掌握了完全的信息，這里就牽扯到信息不對稱問題了。

在這場競猜游戲中，主持人和參與者所獲得的信息當然是不對稱的，主持人知道所有門后獎品的分布，而參與者對此一無所知。主持人在選擇開門的時候，是有所限制的，他既不能打開參與者選定的門，也不能打開其后有獎品的門，這就使得參與者換不換門的概率必然不可能相等。簡單來講，如果把三門推廣到千門，即假設一千扇門里僅有一扇門后有獎品，參與者從一千扇門里頭隨機選一個，主持人再打開998沒有獎品的門，此時再問參與者是否換門，那么參與者必然會換門了。因為他的門是隨機選的，獲勝概率只有1/1000，而主持人知道哪扇門有獎品，所以排除了998扇沒有獎品的門，那么此時換門的獲勝概率則有999/1000。這里可以看出來，從三門到千門，參與者隨機選中有獎品門的概率其實不會隨主持人之后的行動有所改變，然而大部分人并沒有意識到這個事實，而是不自覺地將三門競猜中堅持自己所選門的獲勝概率1/3錯誤地轉換為1/2了。

蒙提霍爾悖論體現的信息不對稱問題，并不僅僅是參與者和主持人對于該競猜節目信息完全度的差異，如果僅是這種層面的信息不對稱現象，顯然并不值得討論。比如說主持人在參與者選門之前就排除了一個錯誤選項，那么盡管雙方信息不對稱，但是公布的規則是顯明的。這種情況下，盡管參與者并不是信息完全的，但是可以正確估計自己的取勝概率，自然就能正確計算出收益的數學期望。

而蒙提霍爾悖論之所以和上述情形不同，是因為參與者對自己獲勝的概率實際上出現了認知錯誤。而這種認知錯誤的產生，恰恰又是主持人代表的主辦方在參與者選擇行為之后，借助信息完全的優勢，采取后續行動刻意制造出來的。參與者在不知道自己的概率估計是錯誤的做出了選擇。例如假若他堅持不換門，他以為取勝概率1/2，實際上卻僅是1/3。這個兩個概率值雖然相差不多，但是卻給了信息優勢者借之牟利的機會。

這里所要關注的并不是信息不對稱現象的普遍性，而要關注信息優勢者利用這種不對稱是否能夠獲利，以及此種利益是否可以通過經濟活動中的長期或者重復博弈予以減少和消除。對于這個問題，蒙提霍爾悖論一定程度上給出了消極的回答，以此換門競猜的游戲為例，該節目舉辦十多年之久，然而參與者大多都沒有意識到換門和不換門兩者的概率是不均等的。

四、信息不對稱與理性人假設

在經濟學學界，信息不對稱理論雖對理性人假設予以批駁，卻并沒有動搖該假設作為經濟學理論基礎的重要地位。理性人假設的核心在于“最大化原則”，亦即作為經濟活動的理性個體都會謀求自身利益最大化，而對自己所處經濟環境的信息完備性或者說豐富性只是為了達成利益最大化理想的附帶要求。也就是說，即便經濟活動的參與者是信息不完備的，但是并不妨礙參與者通過有限的信息去盡量為自己牟取利益。只要經濟活動的參與者意識到自身信息的匱乏，就自然會調高風險預期，并相應地使自己投資等經濟行為偏向保守。所以盡管現實的經濟環境并非如經濟學理論所設定的那么理想，但是經濟活動主體似乎天然具有很強的適應性，能夠依據不同的外部條件調節自己的經濟行為。所以無論是道德風險還是逆向選擇問題，并沒有在根本上反對理性人假設，而僅僅是一種修正和補充。

例如諾貝爾獎得主阿克洛夫所討論的“次品車問題”就揭露了信息不對稱導致的逆向選擇現象，并指出逆向選擇會影響市場資源配置的有效性。“次品車問題”講的是：在二手車市場中，通常有一個二手車的平均價格，并且賣方比買方更清楚自己汽車的狀況，這就導致如果賣方知道自己的車是次品，更樂意以平均價格出售自己的車;而如果自己的車保養的很好，就會覺得平均價格太低，不愿意在二手車市場出售。結果就使得二手車市場出售的車大多價高質次，買方自然不會太樂意在二手車市場上購車。但是考察二手車市場的交易雙方的行為，卻可以發現，他們并非沒有在謀求自身利益最大化。盡管總體而言整個市場資源配置是低效的，但是就每個經濟活動的個體，依然是在做出對自己最有利的行為決策，最終形成了某種總體并非最優的均衡。

蒙提霍爾悖論對于理性人假設則是予以直接質疑的：大眾容易被自己的日常直覺所干擾，使得經濟參與者在計算期望收益時產生極大的偏差。而這種認知偏差，即便是長期或者重復博弈都很難消除。并且陷入這種認知偏差的也不僅僅是一般大眾，高等教育的接受者也不能完全豁免。蒙提霍爾悖論所展現的不過是這種不理性的極端情況，在現實生活中，經濟活動參與者所表現出來的這種不理性是處處可見的，例如博彩等高風險經濟活動屢禁不絕，這些經濟活動的參與者很容易受到信息干擾而高估了自己獲得收益的概率。

雖然大多數的經濟參與者不具有理想化的經濟理性，但是也不必太過悲觀，畢竟即便如蒙提霍爾悖論經過系統性的研究和闡釋，最終還是能夠被大多數人所理解。所以想要在現實層面解決經濟參與者的非理性問題，必須需要將各類認知謬誤多加普及，使之作為背景常識被公眾接受，才能糾正公眾日常直覺導致的認知錯謬，使得經濟運行更為高效和順暢。

參考文獻：

[1]博弈論與信息經濟學[M]. 上海人民出版社 ， 張維迎著， 2004

[2]信息非對稱條件下資本市場[M]. 中國社會科學出版社 ， 孫強，郭樹華著， 2002

[3]博弈論[M]. 中國人民大學出版社 ， （美）朱·弗登博格，（法）讓？梯若爾著， 2002

[4]經濟學[M]. 商務印書館 ， （美）薩繆爾森， 2012

[5]就業、利息和貨幣通論[M]. 商務印書館， （英） 凱恩斯，2006