基于熵權法和改進灰色聚類模型的雷達軟件安全性需求分析

夏 亮，楊江平，鄧 斌，余 娟，宋若愚

(空軍預警學院， 武漢 430019)

analysis

軟件系統本身不會對人員和裝備安全造成直接威脅，但是軟件安全問題可能通過軟、硬件的接口使硬件發生誤動或失效，或者直接導致裝備無法正常運行，造成嚴重的安全事故，目前，對軟件系統安全性研究較少，如何對軟件進行安全性需求分析是一個亟待解決的難題[1-5]。

常見的安全性需求分析方法有濫用用例、橫切威脅、反模型和安全的I*/Tropos等方法，其中Sinder和Opdahl等人給出了濫用用例的組織形式和內容[6]；Haley等人提出從橫切威脅描述中獲取安全需求的方法[7]；Axel等人提出了反模型方法，該方法給出了惡意障礙目標獲取方法和消解惡意障礙目標的方法[8]；劉璘等提出以I*建模活動為基礎，從攻擊者的角度考慮步驟中存在的安全隱患的方法[9]。以上方法都是基于安全分析人員的頭腦風暴，需要的是分析人員的經驗和能力，如果安全分析人員的經驗不足，無法得到有效的結果。

針對這種情況，本研究提出了一種基于熵權法和改進灰色聚類模型的方法對軟件安全性需求進行分析，這種方法可以基于軟件自身的數據去對其安全性需求進行分析，避免了過多的主觀判斷。傳統灰色聚類模型可以解決貧信息聚類分析問題，但是各灰類綜合聚類系數取值相近，導致分析結果不全面。因此，提出了一種改進型灰色聚類模型，充分考慮各個灰類對分析對象重要性判斷的影響，結合熵權法確定分析對象的權重，建立了軟件安全性需求分析模型，并對具體例子舉行計算。

1 雷達軟件安全性需求指標體系建立

根據GJB/Z 142—2004的定義，軟件安全性(software safety)指的是軟件具有的不導致事故發生的能力。而軟件安全(software security)指軟件在受到惡意攻擊的情形下依然能夠繼續正確運行及確保軟件在被授權范圍內合法使用的能力。本研究認為software safety 側重于對無意發生的事故或事件進行的安全保護；而software security 側重于對人為地、有意破壞而進行的安全防護。因此，本文在建立安全性需求指標時將兩者進行綜合考慮，既要考慮到無意發生的事故，即software safety；也要考慮人為的攻擊和破壞，即software security。

在建立安全性需求指標之前，還需要明確安全性指標和可靠性指標的關系，安全性與可靠性既有聯系，又有區別。可靠性是指在一定條件下，在某一時間內軟件完成其規定功能的能力。安全性則是指不能出現導致意外事故的條件或狀態，而不管其規定功能是否完成。也就是說可靠性會考慮軟件所有可能發生的故障，而安全性則考慮能造成軟件安全性事故的故障。

雷達軟件安全性需求指標體系包括漏洞總數、系統癱瘓時間、數據隱藏技術、通信保密技術和構架完整性這五個方面，具體的指標體系如圖1所示。其中漏洞是指能夠被一個或多個威脅利用的資產或控制中的弱點，如果漏洞被攻擊者利用，將會給軟件系統安全帶來嚴重威脅和經濟損失；系統癱瘓時間指的是軟件系統從本次無法正常工作開始到下次正常工作時所經歷的時間，系統癱瘓時間越長，對雷達戰備值班的影響越大，戰爭來臨時可能帶來致命后果，因此，系統癱瘓時間雖然和可靠性有關，但是因為它會帶來嚴重后果，所以將其列為安全性需求指標；數據隱藏技術指的是對于雷達軟件中的一些敏感數據，應當利用數據隱藏技術保護其存在，提高讀取權限，控制其傳播范圍，防止被攻擊者竊取；通信保密技術指的是在雷達數據傳送過程中，對傳輸信道和傳輸設備中傳送的信息采用加密技術的情況；構架完整性指的是軟件全局的安全保護到位和配合情況，各保護措施之間不會因為相互矛盾從而削弱保護強度。

圖1 雷達軟件系統安全性需求指標體系框圖

2 基于熵權法的改進灰色聚類模型

灰色聚類是根據灰色關聯矩陣或灰數的白化權函數將一些觀測指標或觀測對象劃分成若干個可以定義類別的方法[10-12]，本文采取基于熵權法的灰數白化權函數進行建模。傳統的灰色聚類模型如圖2所示，其聚類中心是一個固定點，受相鄰灰類影響較大，難以準確得到分析結果，當分析對象的聚類系數相近時，分析結果會產生較大誤差。針對以上問題，本研究提出了一種改進的白化權函數灰色聚類模型，將聚類中心由一個固定點擴展到一個取值范圍，并結合上下限測度白化權函數得到分析結果，使得到的結果更準確。此外，運用熵權法確定權重可以避免主觀因素的影響，使權重最大程度的保持指標原有的信息。

圖2 傳統灰色聚類模型

在建模之前，需要先明確兩個定義。

定義1設有n個分析對象，m個需求指標，s個不同灰度，根據對象i關于指標j的觀察值xij(i=1,2,…,n，j=1,2,…,m)，將對象i歸于第k個灰類(k∈{1,2,…,s})，稱為灰色聚類。

定義2對于灰類k(k∈{2,3,…,s-1})，稱最可能屬于灰類k的點為其中心點。中心點可以是中點，也可能不是，以屬于灰類k最大可能性為依據。

2.1 指標無量綱化處理

由于指標體系中定量指標的量綱不同，需要對其進行無量綱標準化處理，使指標的取值范圍為[0,1]，采用區別對待的極化差方法對聚類指標xij進行無量綱標準化處理。

對于指標越大越好數值型指標：

(1)

對于指標越小越好數值型指標：

(2)

2.2 熵權法

利用熵權法可以確定各指標的權重，設有n個分析對象，m個需求指標，初始數據矩陣為X=(xij)n×m：

(3)

式中，xij為對象i關于指標j的觀察值。

熵權法確定權重的過程為：

步驟1計算第i個對象在第j個指標下的比重pij：

(4)

步驟2計算指標j的熵值ej：

(5)

步驟3計算指標j的權重wj：

(6)

2.3 改進灰色聚類模型

步驟1確定評價灰類

對于對象i的指標j，設其取值范圍為[aj,bj]。根據分析對象需求，將分析結果劃分為s個灰類，選取最屬于灰類k的區間[λ1,λ2],…,[λ2k-1,λ2k],…,[λ2s-1,λ2s]，確定各個區間端點，將各指標的取值范圍相應劃分為s個灰類。

步驟2構建改進型白化權函數

(7)

(8)

(9)

根據式(7)～式(9),可以得到改進的白化權函數圖,如圖3所示。

圖3 改進灰色聚類模型

步驟3計算單位化綜合聚類系數

(10)

(11)

步驟4判斷灰類

(12)

根據式(12)，可以判斷對象i屬于灰類k*。

2.4 綜合測度決策模型

一般情況下，根據灰色聚類系數向量δi各分量的最大值進行分類，但是當最大主分量與其余主分量差異不顯著時，難以得到準確結論。例如，設k=1,2,3分別對應于好、中、差3個不同灰類，有兩個對象的灰色聚類系數向量分別為δ1=(0.42,0.30,0.28)和δ2=(0.41,0.39,0.20)。如果直接比較聚類系數的最大值，由于0.42>0.41，則對象1優于對象2；但是如果綜合考慮δ1和δ2的各個分量，也可以認為對象2優于對象1。

針對這種問題，可以把灰色聚類系數向量視作一個整體進行研究，提出了一種綜合測度決策模型。

步驟1計算綜合加權決策向量

s-k+2,…,s-1,s,s-1,…,k)

(13)

由式(13)可知，該向量的第k個分量為s，并以此為中心，兩側分量取值依次減1，表明第k個分量對決策對象屬于灰類k的貢獻最大，因此被賦予最大的權重s，其余分量的權重根據與第k個分量的距離確定，距離越近，權重越大。

步驟2計算綜合測度決策系數向量

對象i關于灰類k的灰色綜合測度決策系數的計算公式為：

(14)

步驟3綜合判斷

(15)

由式(15)判定對象i屬于灰類k*。若有多個對象屬于灰類k*，可通過綜合測度決策系數對同屬于灰類k的所有對象進行排序，從而進行決策。

3 實例計算

雷達軟件系統包含終端分系統、監控分系統和信號處理分系統，分別用N1、N2和N3表示，結合雷達軟件系統安全性需求指標體系，采用本文提出的基于熵權和改進灰色聚類模型的方法對雷達軟件系統的3個分系統進行安全性需求分析，得到安全性需求分析結果。

3.1 數據處理

首先按照極化差方法對指標體系中的定量指標進行數據處理，指標體系中的定量數據包括U1、U2，對于定性數據，通過專家打分的德爾菲法得到，同樣也進行無量綱標準化處理，經過處理后的數據如表1所示。

表1 雷達軟件安全性需求指標無量綱化值

3.2 計算權重

其次，利用熵權法計算雷達軟件安全性需求指標的權重，根據式(4)～式(6)，求得指標體系的權重為wj(0.205 3,0.203 8,0.202 3,0.197 5,0.191 1)。

3.3 改進灰色模型求解

然后，根據本文確定的建立改進灰色模型的方法對某型雷達軟件安全性需求分析問題進行求解。

步驟1確定評價灰類

將雷達軟件安全性指標的無量綱化值轉化為百分制，根據各分系統最高、最低分值和灰類劃分需要，在指標區間[50,100]內劃分不重要、一般重要、重要、非常重要4個灰類，取值區間分別為[58,62]、[68,72]、[78,82]、[88,92]。

步驟2構建改進型白化權函數

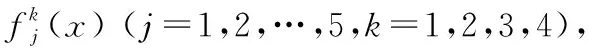
表2 指標的隸屬度情況

表3 單位化綜合聚類系數

步驟4判斷灰類

根據式(12)，判斷雷達軟件分系統N1、N2、N3的最大單位化綜合聚類系數依次為0.737 9、0.667 7、0.540 8，對應的灰類依次為k3、k3、k4。因此雷達軟件終端分系統和監控分系統的安全性需求為重要，信號處理分系統的安全性需求為非常重要。

3.4 綜合測度模型求解

根據判斷結果可知，雷達軟件終端分系統和監控分系統的安全性需求分析結果相同，均為重要，為了對這兩個分系統進一步進行分析和排序，采用綜合測度模型進行求解。

步驟1計算綜合加權決策向量η

根據式(13)，可以求得各個灰類對應的綜合加權決策向量依次為：

步驟2計算綜合測度決策系數向量ρi

根據式(14)，可以求得分系統N1的綜合測度決策系數向量ρ1的各分量依次為：

因此，可以得到ρ1為：

(0.205 9,0.254 9,0.311 5,0.294 1)

同理，可以求得分系統N2的綜合測度決策系數向量ρ2為：

(0.203 5,0.260 8,0.314 3,0.307 8)

步驟3綜合判斷

4 對比分析

表4 傳統模型單位化綜合聚類系數

3個分系統對應的最大單位化綜合聚類系數分別為0.642 3、0.641 8和0.538 9，對應的灰類分別為重要、重要和非常重要。

將傳統灰色聚類模型方法和本文方法進行對比，可以發現兩者的分析結果相同，說明本文的方法具有正確性。但是，兩者也存在一定差異性，比如傳統灰色聚類模型的區分度不如改進灰色聚類模型明顯，改進灰色聚類模型的分析結果更具有說服力，也更準確；此外，傳統灰色聚類模型對于分析結果相近的兩個分系統不能進一步對其重要程度進行判斷，改進灰色模型可以很好地解決這個問題。

5 結論

1) 對雷達軟件系統安全性需求進行了理論分析并建立了雷達軟件安全性需求指標體系；

2) 提出了一種基于熵權法和改進灰色聚類模型的雷達軟件安全性需求分析方法，并建立了相應的模型；

3) 利用該方法對某型雷達軟件的安全性需求進行分析，得到分析結果并對各系統的安全性需求重要程度進行排序；

4) 將該方法與傳統灰色聚類模型進行對比分析，證明了該方法的正確性、科學性和先進性。