靈活選解法 方程巧計算
文焦倩玉
親愛的同學們,你們知道嗎,人類認識一元二次方程的歷史相當久遠。阿拉伯數學家阿爾·花拉子米在他的著作《代數學》里第一次承認了一元二次方程有兩個根,還用幾何學方法得出一般的求根公式,極大地推動了數學的發展。我們都知道解一元二次方程常見的方法有直接開平方法、配方法、公式法和因式分解法,下面我們一起來結合具體題目,合理選擇解一元二次方程的方法,以方便我們的計算。
一、直接開平方法
例1 解方程:(x+1)2-1=3。
【解析】把x+1看作一個整體,將方程兩邊同時加1,變形為(x+1)2=4,再直接開平方,計算即可。
解:(x+1)2-1=3。
(x+1)2=4。
x+1=±2。
x=-1±2。
∴x1=1,x2=-3。
【點評】形如(x+h)2=k(h、k為常數,k≥0)的方程通常使用直接開平方法。需要注意的是,若k=0,則答案需寫作x1=x2=-h的形式,方程有兩個相等的實數根。
二、配方法
例2 解方程:x2-10x+22=0。
【解析】觀察這個一元二次方程,我們發現二次項系數為1,一次項系數為偶數,此時考慮選擇使用配方法。
解:x2-10x=-22。
x2-10x+52=-22+52。
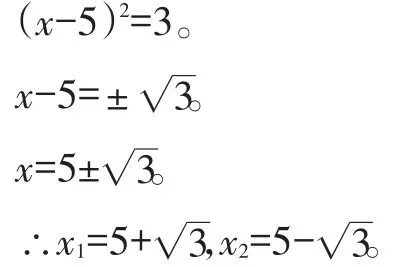
【點評】關于x的一元二次方程ax2+bx+c=0(a、b、c是常數,a≠0),當a=1,b為偶數時通常使用配方法。先把常數項移到方程的右邊,然后加上一次項系數的一半的平方。將方程轉化為(x+h)2=k的形式,進而求解。當一元二次方程的一次項系數不是偶數時,配方容易出錯,同學們應引起注意。
三、公式法
例3 解方程:2x2+x-1=0。
【解析】觀察這個一元二次方程,我們發現二次項系數不為1,一次項系數為奇數,此時應選擇使用公式法。
解:∵a=2,b=1,c=-1,
b2-4ac=12-4×2×(-1)=9。
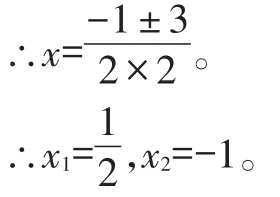
【點評】關于x的一元二次方程ax2+bx+c=0(a、b、c是常數,a≠0),當b2-4ac≥0時,方程的實數根是x=同學們對一元二次方程的求根公式需要熟練掌握,把各項系數的值直接代入公式,進而求解。特別對于a≠1,b為奇數的情況,公式法通常較為簡便。
四、因式分解法
例4 解方程:x(2x-1)=3(1-2x)。
【解析】觀察這個一元二次方程,我們發現2x-1與1-2x互為相反數,移項后可提公因式,因此應選擇使用因式分解法。
解:x(2x-1)-3(1-2x)=0。
x(2x-1)+3(2x-1)=0。
(2x-1)(x+3)=0。
∴2x-1=0或x+3=0。
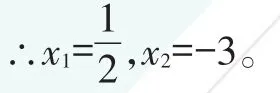
【點評】開始動筆做題之前,同學們一定要養成認真讀題的好習慣。這道題可通過移項,將方程右邊化為0,方程左邊經提公因式之后可分解為兩個一次因式的乘積。把解這樣的一元二次方程轉化為解兩個一元一次方程,從而得出結果。
小弱沮喪地趴在桌上,遠遠看上去就像是喝醉了,不過坐在他身邊的安潔西卻看到他呆滯地盯著地面的眼睛里滿是清醒。
例5 解方程:(3x-1)2-4x2=0。
【解析】將4x2看作2x整體的平方,我們可以利用平方差公式將這個一元二次方程的左邊進行因式分解,轉化成兩個一次因式的乘積。
解:(3x-1)2-(2x)2=0。
(3x-1+2x)(3x-1-2x)=0。
(5x-1)(x-1)=0。
∴5x-1=0或x-1=0。
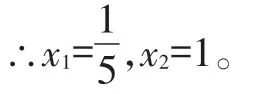
【點評】形如x2-ax=0和x2-a2=0的一元二次方程通常可以使用因式分解法快速地解決。
例6 已知關于x的方程2x2+mx+50=0的一個根是10,求它的另一個根。
【解析】已知一元二次方程的一個根,可以將此根代入方程求出參數的值,再通過解這個方程得到它的另一個根。或者根據題目條件,利用根與系數的關系,進行求解。
解法一:把x=10代入,得2×102+10m+50=0。
解得m=-25。
把m=-25代入,得2x2-25x+50=0。
∵a=2,b=-25,c=50,

【點評】對比本題的這兩種解法,我們可以明顯看出方法2更為便捷。已知一元二次方程ax2+bx+c=0(a、b、c是常數,a≠0)中a和b的值,可以利用x1+x2=進行求解;已知a和c的值,則可以利
例7 已知關于x的方程x2+bx+c=0的兩根分別是 2+1、 2-1,求b、c的值。
【解析】已知一元二次方程的兩個根,那么我們可以直接代入,聯立得到關于b和c的二元一次方程組,進而求解。經過計算,我們發現這種方法并不方便。我們可以逆向使用根與系數的關系,直接得到b和c的值。
解:∵x1+x2=-b,
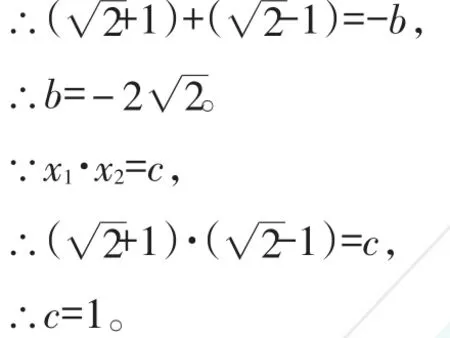
【點評】此處為根與系數的關系的直接應用,同學們要注意歸納總結。另外中,負號不要漏寫。

