角動量守恒定律的應用

李小芳, 王志梅

(1.中北大學信息商務學院， 山西 晉中 030600;2.太原師范學院 物理系， 山西 晉中 030619)

0 引 言

角動量守恒定律是物理學的基本守恒定律之一，大到宇宙天體，小到原子內部都服從這一定律，它在生產、生活、工程技術等方面有著廣泛的應用。

1 角動量守恒定律

角動量定理的微分式為

對一固定點O或轉軸,當物體不受力矩或所受的合外力矩M=0時，物體的角動量L保持不變，這個結論就叫角動量守恒定律[1]。

對于質點，角動量守恒定律的表達式為

L=r×mv=常矢量,

對于剛體，角動量守恒定律的表達式為[1]

L=Jω=常矢量。

2 角動量守恒定律在天體運動方面的應用

2.1 證明開普勒第二定律

開普勒行星運動第二定律，也稱面積定律，指的是對任一行星，太陽和該行星的連線(矢徑)在相等時間內掃過的面積相等。現用角動量守恒定律證明。

行星對太陽角動量的大小為

L=rmvsinθ,

(1)

式中：m----行星的質量;

θ----矢徑r與速度v之間的夾角，行星速率

則

(2)

式(2)中

rsinθds=r⊥ds=2dA,

(3)

其中，dA為行星矢徑在dt時間內掃過的面積，因此

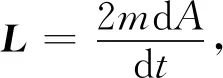
(4)

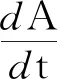
由于太陽和行星之間的萬有引力為有心力，它對力心的力矩為零，故行星的角動量守恒，即L=常量，因此

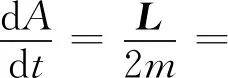
從而證明了行星的矢徑在相同時間內掃過的面積相同。事實上，開普勒第二定律與角動量守恒定律等價。

2.2 證明太陽在焦點位置

開普勒第一定律：每一行星沿各自的橢圓軌道環繞太陽，而太陽則處在橢圓的一個焦點上。現用角動量守恒定律及牛頓力學理論證明太陽處在橢圓的一個焦點上。

設橢圓方程為

式中：a----長軸;

b----短軸。

焦點位置為(0,±c)，且a2-c2=b2。

行星繞太陽運動時，行星所受的力矩為零，角動量守恒。由角動量守恒定律，得

r1mv1=r2mv2,

(5)

式中:v1,r1----分別為行星處于遠日點時的速率及距太陽的距離;

v2,r2----分別為行星處于近日點時的速率及距太陽的距離。

由式(5)得

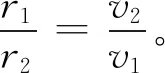
(6)

由于萬有引力為保守力，只有保守力做功時，機械能守恒。由機械能守恒定律，得

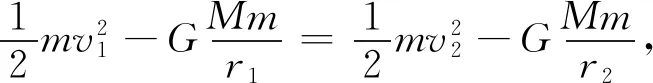
(7)

整理上式得

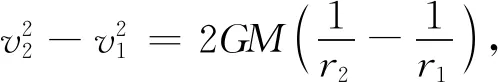
(8)

由向心力公式，得

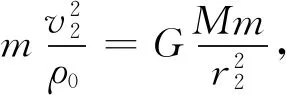
(9)

式(9)中長軸端點弧元的曲率半徑

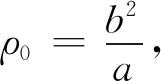
(10)

由式(6)、式(8)～式(10)得

r1r2=aρ0=b2，

(11)

又因為

r1+r2=2a,

(12)

聯立式(11)和式(12)得

r2=a-c,

(13)

證明了太陽的位置為橢圓的焦點。

2.3 定性解釋星系的扁平狀旋轉結構

對于很多星系來說，它們都是扁平狀旋轉結構。數學家拉普拉斯的“星云說”指出，星系旋轉盤狀結構的成因是角動量守恒。對于星系來說，其一開始是一個緩慢旋轉的球狀氣體云，具有初始角動量。在垂直于軸向的徑向上，星系由于引力作用慢慢向內收縮，因為引力為有心力，因此星系對轉軸的角動量L=rmv守恒，當星系半徑減小時，其速率增大，離心力也隨之增大，當離心力增大至與引力恰好平衡時，星系停止收縮。對于軸向不存在離心力，則星系持續收縮，最終在引力的作用下，軸向變得非常扁平。因此星系形成了具有一定半徑大小的扁平狀旋轉結構[2]。

圖1 天體的旋轉盤狀結構

3 角動量守恒定律在工程技術方面的應用

3.1 進動陀螺儀

陀螺儀有兩個特性：進動性和定軸性，這兩種特性都是建立在角動量守恒的原則下[3]。

3.1.1 陀螺的進動

陀螺在繞自身對稱軸高速轉動的同時，其對稱軸繞經過定點的豎直軸轉動，這種高速自轉物體的轉軸在空間轉動的現象叫做進動[4]。

陀螺的旋進如圖2所示。

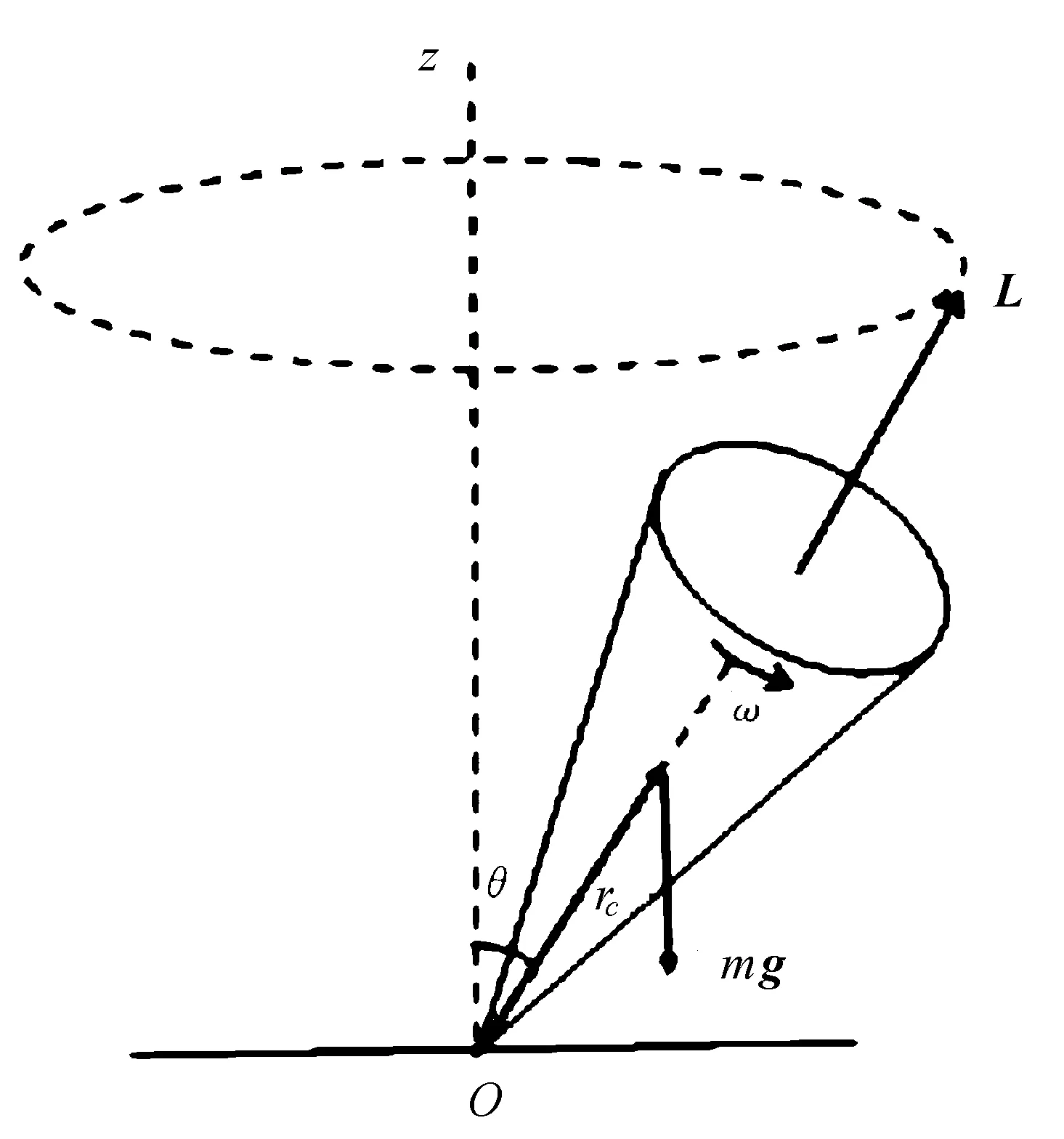
(a) 自轉陀螺的對稱軸同時繞OZ軸轉動

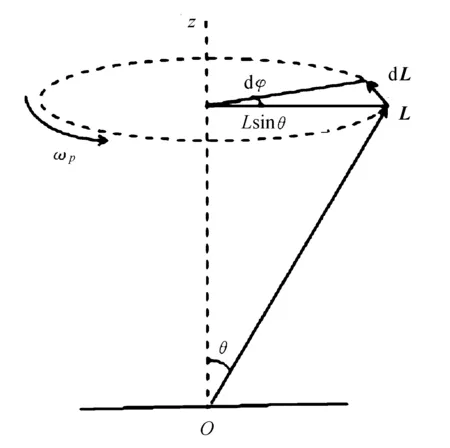
(b) 陀螺的對稱軸轉動一定的角位移圖2 陀螺的旋進

圖2(a)中，質量均勻對稱分布的陀螺在高速旋轉時，相對于O點的角動量為

L=Jω，

(14)

式中：J----陀螺的轉動慣量;

ω----自轉角速度。

L的方向沿對稱軸，由于陀螺質量對稱分布，此角動量就是陀螺對自身對稱軸的角動量。高速旋轉的陀螺，在傾斜狀態時，由于進動產生對O點的角動量遠小于其本身對稱軸的角動量，可將總角動量近似為對其自身對稱軸的角動量。

以O點為參考點，只有重力產生力矩，重力的力矩

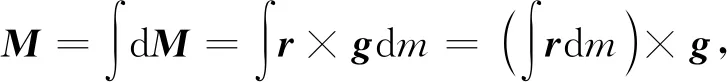
(15)

式中：dm----陀螺上小質元的質量;

r----質元相對于O點的位置矢量。

整理上式，得

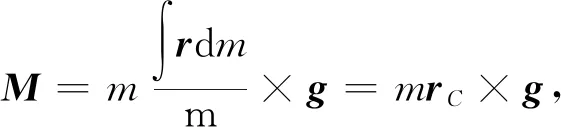
(16)

式中：rC----質心相對于O點的位置矢量。

由于rC與L同向，因此重力對O點的力矩M始終與角動量L垂直。

在重力矩的作用下，dt時間內，陀螺自旋角動量的增量

dL=Mdt=mrC×gdt。

(17)

方向垂直于紙面向里，與L方向垂直。所以在重力矩的作用下，陀螺的自旋角動量大小不變，只改變方向，L的末端軌跡為圓。

圖2(b)中，陀螺對稱軸與豎直軸之間的夾角為θ，dt時間內，陀螺對稱軸轉過的角位移為dφ，自旋角動量的增量大小

|dL|=Lsinθdφ。

(18)

陀螺重力矩的大小

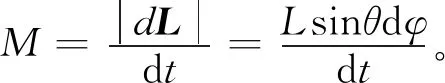
(19)

因此,陀螺的進動角速度為

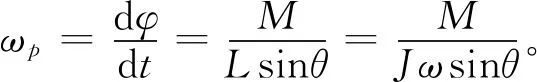
(20)

將式(16)代入式(20)，得

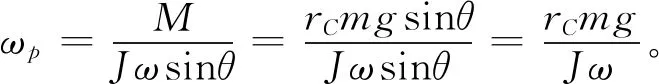
(21)

即進動角速度ωp與陀螺自轉角速度成反比，與角度θ無關。ωp隨自轉角速度的增大而減小，自轉角速度越大，陀螺越容易穩定旋轉。當陀螺的自轉角速度不夠大時，則除了自轉和進動外，陀螺的對稱軸還會在鉛垂面內上下擺動，稱為章動[2]。

3.1.2 陀螺儀

陀螺儀如圖3所示。

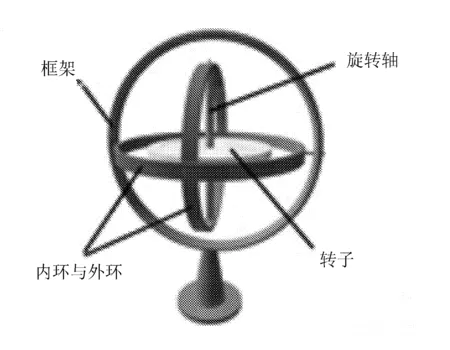
圖3 陀螺儀

從圖3可以看出，陀螺儀的轉子、內環、外環都可以繞著各自的轉動軸自由轉動，三個轉動軸正交于轉子質心，在忽略摩擦和空氣阻力的情況下，這種設計保證了轉子所受的合外力矩為零，轉子的角動量L=Jω守恒。陀螺儀的轉動慣量J不隨時間變化，若將陀螺儀的轉軸指向某方向，當轉子繞自身對稱軸以角速度ω高速轉動時，不管如何改變框架的方位，其中心軸的空間取向都始終保持不變，因而具有導航能力[5-6]。

高速轉動的陀螺儀受到一定的干擾力矩后，轉子的對稱軸會在初始方位附近產生幅度很小的短時高頻章動，保證對稱軸的方向基本不變，因此具有極強的穩定性。但是如果陀螺儀持續受到干擾力矩的話，對稱軸的指向會隨時間產生誤差。

我國的WS-35型155 mm口徑制導炮彈，其最大射程可達到100 km，且精確度高，使用“北斗”衛星導航系統進行GPS/慣性制導(INS)。慣性制導的核心部件為三軸陀螺儀，其抗干擾能力和自主性強，但是存在導航精度隨時間不斷降低的問題。利用GPS的長期穩定性與適中精度可以不斷對INS加以校準，消除INS積累的誤差[7]。

3.2 直升飛機螺旋槳

直升飛機一般都有兩個螺旋槳。當直升機靜止在地面時，受到重力及地面給它的支持力，兩力產生的合外力矩為零，直升機的角動量守恒。飛機靜止在地面時，初始角動量為零，當直升飛機的主螺旋槳旋轉時，機身必然會朝著反方向旋轉。為了阻止機身旋轉，需要另一個螺旋槳來產生阻力矩，使其與主螺旋槳產生的力矩相抵消。大多數直升機通過在尾部安裝一個螺旋槳來阻止機身轉動，但也有直升機采用反向轉動的雙旋翼來阻止機身旋轉，“共軸雙槳”與“縱列式雙槳”的直升機分別如圖4和圖5所示。

圖4 俄羅斯制造的卡50直升機

圖5 雪地降落的支努干飛機

4 角動量守恒定律在游戲和體育方面的應用

4.1 扔水瓶挑戰

“扔水瓶挑戰”是一個風靡于社交網站的游戲，向空中旋轉扔出一個裝有部分水的瓶子，瓶子在空中翻一個跟頭后，可以平穩垂直地站立在桌面或地面上。下面分析一下“扔水瓶挑戰”背后所蘊含的物理知識。

在忽略空氣阻力的情況下，水瓶被扔出去之后，只受重力，且重力通過質心，因此系統所受的合外力矩為零，角動量L=Jω守恒。由于水具有流動性，當瓶子在空中旋轉時，瓶內的水并不會隨著瓶子旋轉，而是沿著瓶子晃動，導致水的質量沿著瓶子重新分布，從而改變了系統的轉動慣量。

文獻[7]構建了一個簡單的一維模型來研究在空中旋轉的水瓶，導出了系統的質心和轉動慣量

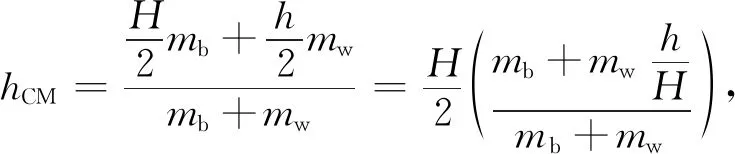
(22)

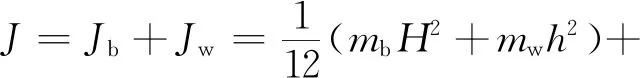
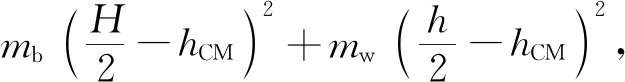
(23)

式中:hCM----系統質心的位置;

J----系統的轉動慣量;

Jb、Jw----分別為瓶子和水的轉動慣量;

mb----瓶子的質量;

mw----瓶中水的質量;

H----瓶子的高度;

h----瓶中水的高度。

水瓶在旋轉過程中，水的高度h時刻變化，因此,系統的質心和轉動慣量也隨時變化。水在瓶中晃動的時候，由于水的質量沿著瓶子分散分布，導致系統的轉動慣量增大[8-9]。

根據角動量守恒定律，當系統的轉動慣量增大時，其旋轉角速度會減小。因此水瓶在落地時角速度較小，可以平穩垂直地站立在桌面或地面上。若游戲中使用空瓶子或裝滿水的瓶子，則挑戰很難成功。空瓶子或裝滿水的瓶子在轉動過程中可看成剛體，其轉動慣量不變，水瓶旋轉時角速度就會保持不變，水瓶落地時旋轉角速度大，導致挑戰失敗。

“扔水瓶挑戰”成功的關鍵有兩個：一是盡量減小落地的角速度；二是盡可能降低系統的重心，重心越低系統越穩定。挑戰時，瓶中的水不能太少也不能太多。水太少，系統的重心雖低，但其轉動慣量增大不明顯；水太多，系統重心不僅高，而且水在瓶中晃動不明顯，對改變轉動慣量沒有太大貢獻。經過實驗和分析[8-9]，當瓶中的水為1/3～1/4時，“扔水瓶挑戰”最容易成功。

4.2 體育賽事

體育賽事中的許多運動，同樣是通過改變運動員自身的質量分布來改變旋轉時的角速度，從而使表演更具有觀賞性。

跳水運動員、花樣滑冰運動員經常會做一些旋轉動作，這些運動員的旋轉速度可以通過改變肢體動作來實現。在阻力可以忽略不計的情況下，不論運動員在地面上旋轉還是空中旋轉，所受的合外力矩都為零，因此角動量守恒。當運動員收攏雙臂或腿時，其轉動慣量減小，旋轉速度增大；當運動員伸開雙臂或腿時，其轉動慣量增大，旋轉速度減小。

5 結 語

角動量守恒定律在諸多領域都有體現，是一個非常重要的理論，除了文中介紹的應用外，生活中很多常見現象也蘊含著角動量守恒定律的知識，因此角動量守恒定律及其應用研究非常重要。