一字型鋼管束混凝土剪力墻軸壓力學性能有限元分析

孫 浩,萬青青,楊秋寧,李宏波

(寧夏大學 a.土木與水利工程學院;b.寧夏節水灌溉與水資源調控工程技術研究中心;c.旱區現代農業水資源高效利用教育部工程研究中心,銀川 750021)

0 引 言

剪力墻具有空間布置靈活、抗剪切剛度高、整體抗震性能優良等優點，被廣泛應用于各類公共建筑中。隨著高層建筑結構的發展,傳統的鋼筋混凝土剪力墻的承載力和抗震性能已不能滿足現實需求,且在地震高烈度區域的使用受到限制。近年來,鋼管混凝土結構在建筑領域中發展迅速,備受建筑設計師的青睞。鋼管混凝土是在鋼管中填充混凝土,且鋼管及其核心混凝土能共同承受外荷載作用的結構構件[1]。鋼管混凝土結構具有承載力高、抗震性能優越、耐火性能好等優點,被廣泛用于高層和超高層建筑中。

目前,國內外對鋼管約束混凝土軸壓構件進行了大量的研究： 任慶新等[2-3]對圓鋼管混凝土短斜柱和橢圓形鋼管混凝土長柱軸進行試驗研究及理論分析; 文獻[4-8]對方鋼管約束混凝土短柱軸壓力學性能進行研究, 以上試驗及研究結果表明, 混凝土立方體抗壓強度是決定鋼管混凝土軸壓破壞模式的主要因素。 Rong等[9]對L形鋼管混凝土短柱的軸壓性能進行理論分析及試驗研究,得出的理論值、 試驗值與數值模擬結果吻合良好; 楊曉杰等[10]提出隨著鋼管壁厚的增加, 短柱塑性變形能力提高,塑性破壞角變大; 文獻[11-12]研究了帶暗支撐鋼筋混凝土短肢剪力墻的模型問題; 張敏等[13]對局部設縫剪力墻的問題進行了試驗; 文獻[14-15]對型鋼混凝土短肢剪力墻受力性能進行了研究。 以上試驗結果表明： 設置暗支撐、 局部設縫和型鋼的剪力墻抗震性能顯著提高, 但是設置暗支撐、 局部設縫和型鋼在施工時不僅增加了施工難度, 而且不能保證混凝土的澆筑質量, 設縫雖然提高了延性, 但其承載力和剛度明顯下降。 所以本課題組提出了鋼管束混凝土組合剪力墻改善鋼筋混凝土短肢剪力墻的力學性能。

對于中國西北地區,由于經濟和地域的原因,多高層結構和鋼管混凝土組合結構的發展受到了限制。為了改善這一問題,更好地推動鋼管混凝土組合結構的發展與應用,提高經濟效益,優化施工工藝,本文建立了9個一字型鋼管束混凝土剪力墻的有限元模型,選出最優鋼管束管壁厚度,為實際工程應用提供一定的理論基礎和技術支持。

1 工程背景

本次有限元分析以銀川市洪廣鎮洪鑫苑城市棚戶區改造項目為背景。為推進“棚戶區”的改造工作,在與寧夏遠高綠色科技建筑有限公司共同合作的基礎上,進行試驗驗證,為實際工程作參考。圖1為本次有限元模擬的實體鋼管及其鋼管束生產線。在該項目中,多處運用鋼管束構件，如圖2所示,實現了工廠式流水施工生產。全面提升了住宅綜合品質,大幅提高了勞動生產率,節能減排效果顯著,有利于環境保護、實現文明施工、降低建造成本,提高了經濟效益,符合科學發展的要求。

2 有限元模型的建立

基于一字型多腔鋼管混凝土短柱,采用大型有限元軟件建立有限元模型進行短柱軸壓力學性能分析。

2.1 模型尺寸設計

鋼管束管壁厚度為6 mm時, 每個腔體內部為88 mm×88 mm, 高為300 mm, 平面尺寸見圖3。

圖1 鋼管束生產線Fig.1 Steel tube bundle production line

圖2 鋼管束構件Fig.2 Steel tube beam components

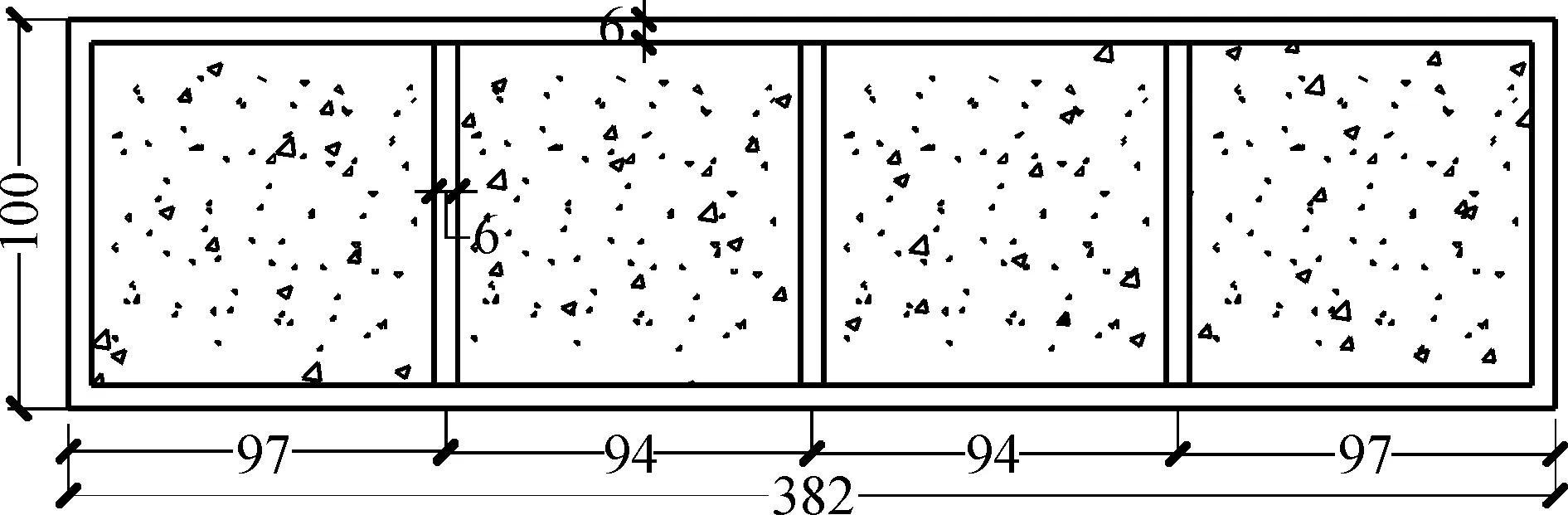
圖3 試件幾何尺寸示意圖Fig.3 Schematic of geometric dimensions of specimens

2.2 材料本構模型材料

鋼材采用單向荷載作用下應力-應變五階段本構模型[16], 如圖4所示 。鋼管在三向應力狀態下,應力強度和應變強度[16]分別見式(1)和式(2)。 鋼材的彈性模量Es和泊松比μ依據《鋼結構設計規范》(GB 50017—2003)分別取2.06×105MPa和0.283， 其中fp=190 MPa、fy=241 MPa、fu=539 MPa。

(1)

圖4 應力-應變五階段本構模型Fig.4 Five-stage stress-strain constitutive model

核心區混凝土采用分解分析法得到的核心混凝土的應力-應變關系曲線[15]為

(3)

該本構關系使用方便,能夠較好地表現出軸壓條件下鋼管對混凝土的約束作用。式中:

εc=1 300+10fcu；

A=2-K；B=1-K；

其中，fcu為混凝土立方體抗壓強度(MPa);fck為混凝土軸心抗壓強度標準值(MPa);ξ為混凝土界限相對受壓區高度;ε0核心混凝土環向應變;fy為鋼材屈服點(MPa);As為鋼筋的面積(mm2);Ac為混凝土的截面面積(mm2)。

表1 混凝土塑性損傷參數

注:fb0/fc0為初始等效雙軸壓縮屈服應力與單軸抗壓縮屈服應力之比;K為第二應力不變量之比, 其定義了混凝土在屈服平面在偏平面上的形狀。

2.3 相互作用與邊界條件

本模型的相互作用分為4種:第一種是邊界耦合與參考點的約束;第二種是混凝土與鋼管之間的表面-表面接觸,定義切向行為庫倫罰摩擦為0.3,切向為“硬接觸”;第三種是外包鋼管與加載板之間的Tie連接;第四種是混凝土與加載板之間的Tie連接。對于加載板兩端設置鉸接邊界條件,用于模擬在試驗機上的平板鉸加載模式,加載方式為位移加載,使模型更易收斂。

2.4 網格劃分與單元選擇

為提高計算機運算模型的效率,對于研究構件截面承載力,并考慮主從面的關系,對加載板設置30 mm×30 mm的網格,混凝土設置22 mm×22 mm的網格,鋼管設置10 mm×10 mm的密布網格。上下加載板與混凝土采用隱式求解器下三維實體縮減積分單元(C3D8R);一字型鋼管采用四節點縮減積分殼單元(S4R)。為保證結果的精確性,殼體單元在厚度方向上設置9個積分點。

3 模擬結果及分析

3.1 整體受力過程

對9個鋼管束混凝土短柱在軸心荷載作用下的受力過程進行對比和分析。鋼管束混凝土的示意圖如圖5所示。鋼管混凝土每個腔為88 mm×88 mm，高300 mm,鋼管的厚度分別為3、6和9 mm,混凝土的強度等級分別為C30、C40和C50。圖6—圖8分為混凝土強度為C30、C40、C50對應的3、6和9 mm對應的荷載-位移曲線。

由于該模型的套箍系數分別為1.65、1.23和1,故工作分為彈性、彈塑性和強化3個階段。為了敘述方便,在圖8所示的荷載-位移曲線上選取3個特征點A、B和C點。

圖5 鋼管束混凝土剪力墻整體示意圖Fig.5 Steel tube confined concrete shear walls

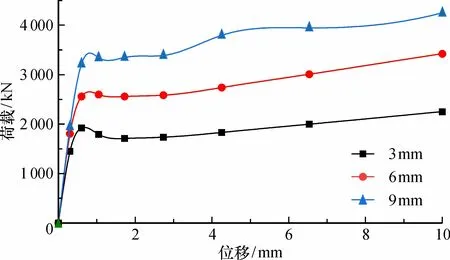
圖6 混凝土強度為C30時不同鋼管厚度下的荷載-位移曲線Fig.6 Load-displacement curves for different steel tube thickness with concrete strength of C30

圖7 混凝土強度為C40時不同鋼管厚度下的荷載-位移曲線Fig.7 Load-displacement curves for different steel tube thickness with concrete strength of C40

圖8 混凝土強度為C50時不同鋼管厚度下的荷載-位移曲線Fig.8 Load-displacement curves for different steel tube thickness with concrete strength of C50

(1)彈性階段(OA):該階段荷載-位移曲線接近直線,在鋼管應力達到比例極限時停止。在這一階段,由于混凝土和鋼材的泊松比μ不同,鋼管橫向變形的能力大于混凝土橫向變形的能力,二者單獨受力,沒有協同工作,此時構件的承載能力等于內置混凝土和鋼管束承載力的簡單疊加。

(2)彈塑性階段(AB): 鋼管進入彈塑性工作階段, 由于該階段鋼材的彈性模量Es不斷減小, 而核心混凝土的彈性模量無明顯變化, 這使得鋼管與核心混凝土之間在軸力分配的比例上不斷改變, 核心區混凝土受力不斷增加, 鋼管受力不斷減小。 當核心區混凝土的泊松比超過鋼管的泊松比時, 二者開始產生相互作用力——緊箍力p, 這時的鋼管與核心區混凝土均處于三向應力狀態, 在構件腹板的中部出現明顯的鼓曲現象, 如圖9所示。

圖9 腹板中部鼓曲圖Fig.9 Chord in the middle of the web

(3)強化階段(BC):在該階段，荷載主要由核心混凝土承擔,核心區混凝土的橫向變形增大,且泊松比遠遠大于鋼管的泊松比,混凝土徑向擠壓鋼管,這使得鋼管環向應力增大。根據Von Mises屈服條件,環向應力增大的同時徑向應力隨之下降,核心混凝土由于環向應力的增大而提高了承載能力。這就是雖然核心混凝土已經破碎,但是由于受到鋼管的約束,承載能力卻一直在上升的原因。

3.2 核心混凝土縱向應力分析

圖10為混凝土H/2高的特征點, 圖11給出在峰值荷載作用下鋼管厚度為6 mm, 內核心混凝土立方體抗壓強度為30 MPa時的應力-應變關系曲線, 施加不同荷載, 核心混凝土縱向應力的分布狀況。 在同一截面高度, 核心混凝土的縱向應力不同。 這表明, 進入彈塑性階段以后, 受壓區核心混凝土開始與鋼管束協同工作。 角點處核心混凝土的縱向應力大于內隔板兩側點和中心點處的核心混凝土的縱向應力, 角點處的最大應力達到了60 MPa, 比其他部位應力高50%左右,原因是鋼管束對靠近角點處的約束作用最大。

圖10 H/2高處混凝土特征點Fig.10 Concrete feature points at H/2 height

圖11 峰值荷載作用下混凝土各點縱向應力-應變關系曲線Fig.11 Longitudinal stress-strain curves of concrete at each point under peak load

圖12為鋼管束特征點示意圖,特征點分布在高度為H/2的截面上。圖13為鋼板外側點、內側點應力-應變關系曲線。在荷載施加的初期,應力-應變曲線呈線性關系。隨著軸向荷載的增加,核心混凝土和多腔鋼管的應力和應變增大,當應變達到2×10-3時,鋼材腹板內外出現應力差,并且隨著荷載的不斷增大,應力差也不斷增大。這說明鋼管腹板處開始出現局部彎曲變形。由圖14內隔板中點應力-應變關系可知,當鋼板達到Von Mises應力屈服的同時,縱向應力也同時達到了峰值,即多腔鋼管的軸向荷載達到了最大值。隨著軸向荷載的增加,縱向應力開始下降,環向應力逐漸上升,這說明混凝土的橫向變形已經漸漸大于多腔鋼管的橫向變形, 鋼管約束核心混凝土的橫向變形。 因為鋼板屈服后服從Von Mises屈服準則, 所以在環向應力不斷上升的同時, 縱向應力必然下降,鋼材自此進入彈塑性階段。

圖13 鋼板內、外側應力-應變曲線Fig.13 Stress-strain curves of inner and outer steel plate

圖14 內隔板中點應力-應變曲線Fig.14 Stress-strain curves of inner midpoint

3.4 參數分析

3.4.1 混凝土的立方體抗壓強度 由圖15可知,隨著混凝土抗壓強度的提高以及鋼管束混凝土短柱初始剛度的增加,承載能力也隨之提高,強化段趨勢幾乎相同,變形能力相差不大。

3.4.2 鋼管束管壁的厚度 由圖6—圖8可知,當鋼管束管壁厚度增大時, 隨著軸向位移的增加,曲線有靠近縱坐標的趨勢,鋼管束混凝土短柱的剛度逐漸增大。由圖15可知,隨著鋼管束管壁厚度的增加,試件的極限承載力逐漸升高,但是構件的極限位移變化不大。原因可能是隨著鋼管束管壁厚度的增加,構件的含鋼率逐漸提高,核心區混凝土受到更大的緊箍力p。對于C30混凝土,每增加3 mm厚的鋼管束，混凝土極限承載力分別提升56%和24%;對于C40混凝土,每增加3 mm厚的鋼管束，混凝土極限承載力分別提升62.3%和29%;對于C50混凝土,每增加3 mm厚的鋼管束，混凝土極限承載力分別提升62.7%和30.4%。由此得出,隨著緊箍力的減小,增加鋼管束管壁的厚度,提升極限承載力的效果越好。

圖15 不同鋼管束管壁厚度和混凝土強度下的最大承載力Fig.15 Maximum bearing capacity of steel tube with different thickness and concrete strength

4 結 論

通過建立9組鋼管束混凝土有限元模型,分析了一字型鋼管束混凝土剪力墻的受壓全過程及參數對鋼管束混凝土軸壓性能的影響,得出如下結論:

(1) 一字型鋼管束混凝土剪力墻具有較高的承載力及較強的變形性能,在核心混凝土進入彈塑性階段后,鋼管束對核心混凝土產生約束作用。相同厚度的鋼管束管壁,鋼管束對混凝土的角點處約束效果最優,角點處應力相比中心點、內隔板兩側點、腹板中點均提高50%左右。

(2) 隨著混凝土強度等級的增加,不同鋼管束管壁厚度的一字型鋼管束混凝土短柱的承載力均有不同程度的提高。對于C30混凝土,每增加3 mm厚的鋼管束，混凝土極限承載力分別提升了56%和24%。對于C40混凝土,每增加3 mm厚的鋼管束，混凝土極限承載力分別提升了62.3%和29%。對于C50混凝土,每增加3 mm厚的鋼管束管壁厚度，混凝土極限承載力分別提升了62.7%和30.4%。

(3) 在混凝土強度相同條件下,增加鋼管束管壁的厚度,其極限承載力的提升幅度呈現先增加后減小的趨勢,對于C50混凝土,從3 mm到6 mm時極限承載力增加最為明顯,其極限承載力增加了63.7%;不同等級強度混凝土,鋼管束管壁厚度為6 mm時,其承載力提升的幅度最為顯著。