角度自適應離散縱標輸運計算方法

陳義學，張 斌

(華北電力大學 核科學與工程學院，北京 102206)

粒子輸運計算在許多領域起到至關重要的作用，如核裝置的屏蔽設計[1]、聚變中子學、輻射治療應用[2]和天體物理等。隨著計算機軟件和硬件技術的快速發展，粒子輸運模擬逐漸成為研究科學問題的重要手段。在屏蔽計算方面，輻射屏蔽安全是核能安全的重要組成部分，輸運計算方法的研究為輻射屏蔽設計提供有力支撐。穩態中子輸運方程是一個包含能量、空間和角度變量的六維方程[3-4]，同時由于實際屏蔽模型幾何材料的復雜性和非均勻性，三維大規模高保真粒子輸運模擬極具挑戰。目前的屏蔽計算由于計算條件和計算時間的限制，在物理和幾何方面采用了大量近似處理，實際經驗可以修正近似引入的不確定性。然而，不同屏蔽問題的特性差異較大，已有的屏蔽計算經驗適應性不強。隨著核能技術的發展，一些復雜屏蔽輸運問題的出現，如孔道屏蔽問題[5]、聚變堆深穿透問題、醫學物理等，傳統屏蔽計算方法存在局限性，導致屏蔽計算的精度和速度均受到極大影響。

離散縱標法(SN)具有計算速度較快、精度較高、適合求解深穿透輸運問題等優點，在屏蔽計算中得到廣泛應用。SN對輸運方程的方向變量采用直接離散的方式，將原來連續的方向變量轉換為有限的離散方向求解。在角通量密度各向異性較強的物理模型中，當離散求積組數值積分角通量密度精度較低時，會導致射線效應問題[6-8]，使標通量密度呈現空間震蕩如鋸齒波紋狀分布。射線效應極大影響了屏蔽計算的精度及輻射屏蔽設計的可靠性。對于具有孤立點源、大空腔或孔道的屏蔽問題，射線效應更加嚴重，因此有必要研究精確、可靠的屏蔽計算方法。實際屏蔽計算模型中輸運方程變量的離散導致極大的耦合線性方程組，在計算機存儲和快速求解方面都存在挑戰，這是粒子輸運模擬的難點。為有效地利用計算資源，本文采用角度自適應方法求解輸運問題[9-11]。

1 自適應離散求積組

自適應方法根據計算過程中處理數據的特征自動調整求解參數，是求解偏微分方程的一種方法。數值求解過程中自動調整計算所需網格，產生最佳的離散方式，從而以盡量少的計算量達到要求的精度。角度自適應方法基于角度變量的局部細化[12-14]，采用相對于均勻角度離散較少的離散方向，有效地提高屏蔽計算精度。自適應方法成功應用的關鍵因素有：可靠的局部誤差估計，用以評價局部區域的離散誤差；靈活的數據結構，便于程序實現與應用；不同細化層之間的數據傳遞的延拓和限制算子。

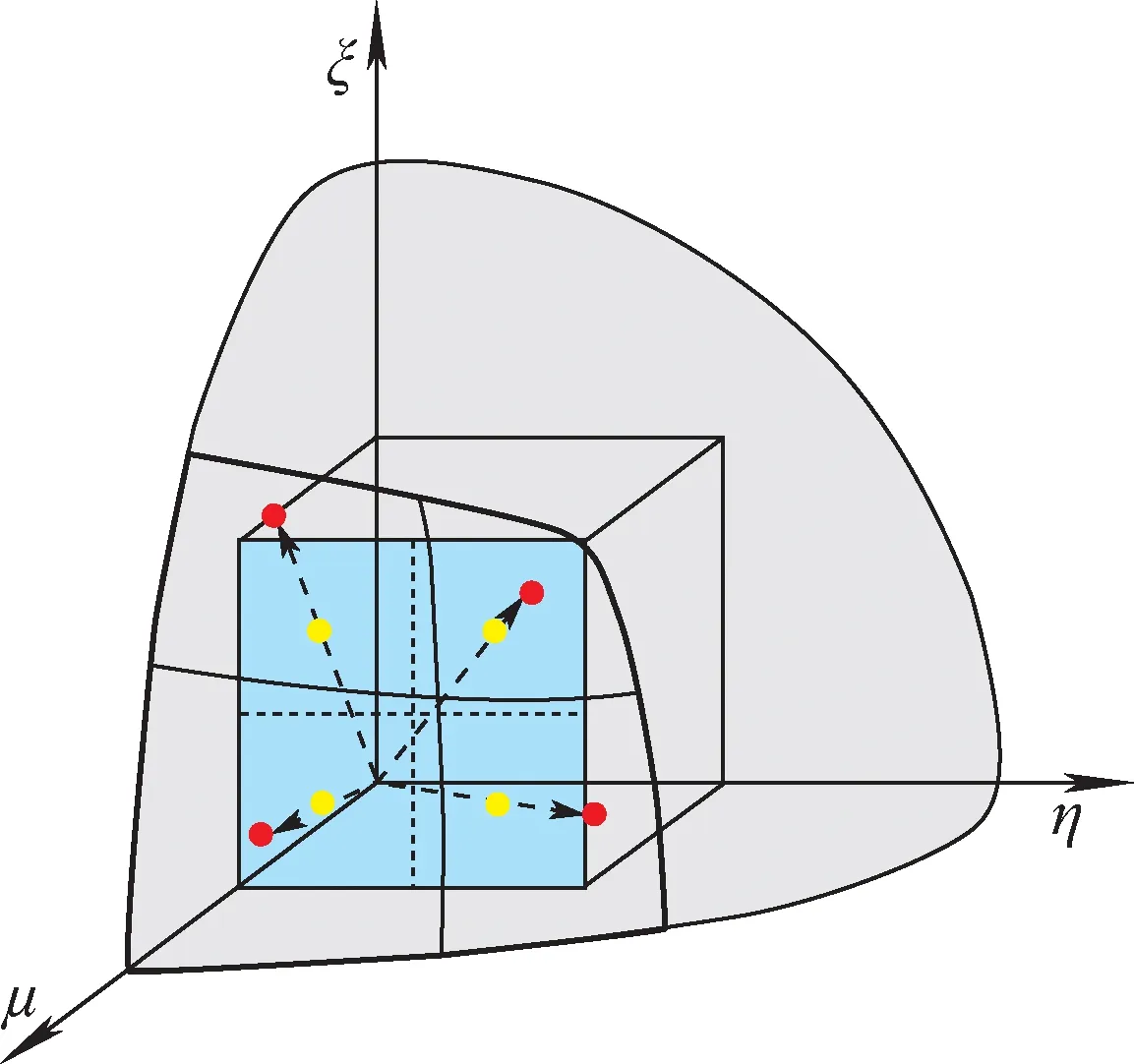
圖1 立方體的外接圓Fig.1 Cube inscribed into unit sphere

實際屏蔽計算問題中，在局部角度區域內經常出現角通量密度間斷或接近間斷的情況，自適應離散求積組應具備在較小的角度區域內精確計算通量矩的能力，同時還需要具有局部角度區域可細化、權重系數非負和離散方向數不受限制等特征。自適應離散求積組的構造，將1個立方體鑲嵌到單位球內，立方體的每個角對應每個卦限，如圖1所示。在立方體表面上劃分出若干四邊形，在每個四邊形內定義離散方向，向單位球面投影得到求積點，通過細化四邊形的劃分來細化離散方向。每個平面四邊形包含4個坐標點，從單位球的原點到每個坐標點的矢量確定唯一的離散方向，每個球面四邊形內對應有4個離散方向。采用中心點法確定坐標點，平面四邊形內4個子四邊形各自的中點作為坐標點。求積組的所有離散方向確定后，每個平面四邊形對應的球面四邊形的面積作為該求積點的權重系數。

任意局部角度區域的細化功能是自適應離散求積組的優點之一，當角通量密度在局部角度區域內不光滑，甚至出現間斷或接近間斷的情況時，在局部角度區域內細化離散方向，局部細化的求積組具有分層的數據結構。1個卦限對應的3個四邊形上分別采用二階、三階和四階細化求積組的情況，如圖2所示。

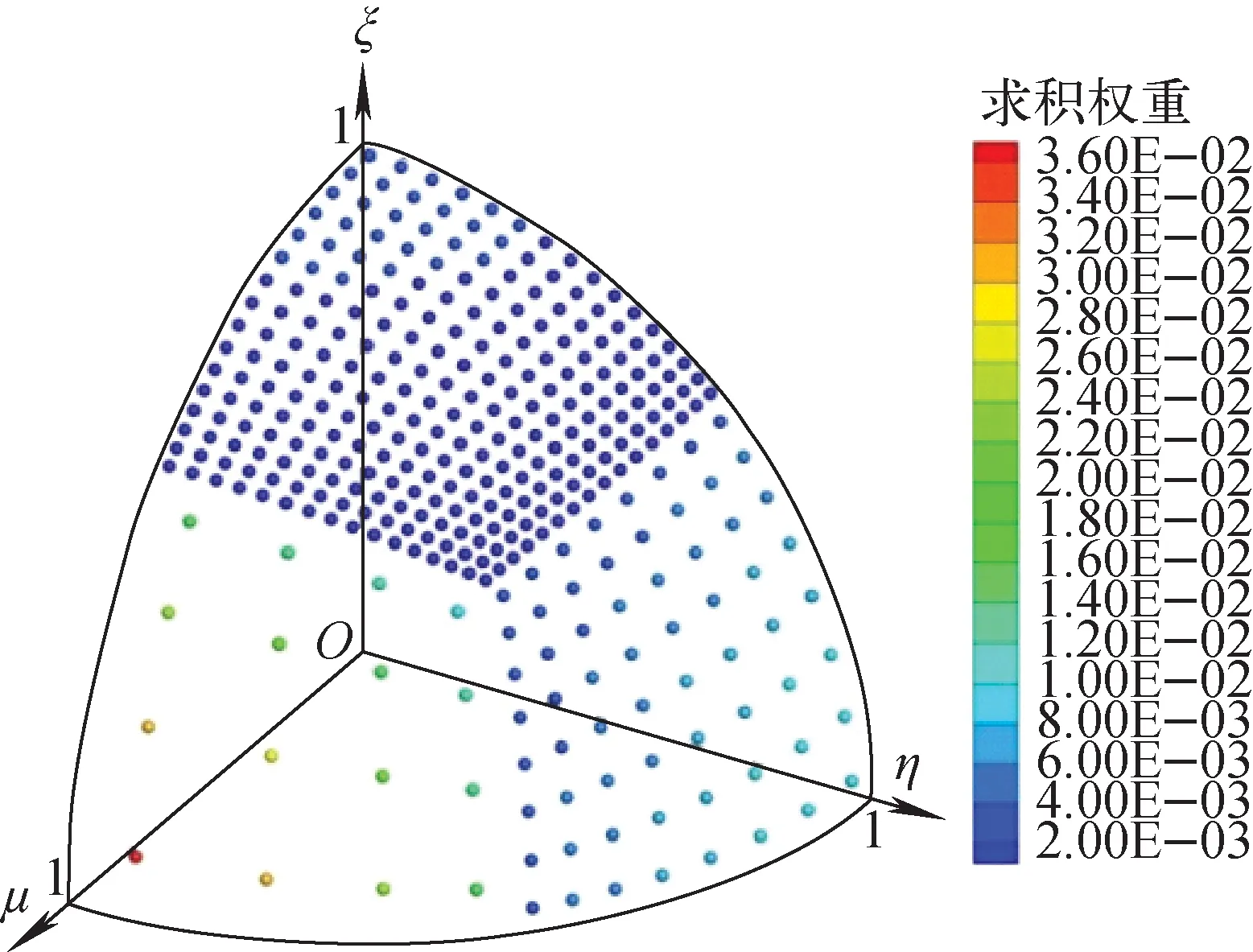
圖2 局部區域細化求積組Fig.2 Local quadrature set refinement

2 角度自適應方法

角度自適應方法在角通量密度梯度較大或間斷的區域進行局部細化，能提供較好的數值近似。另一方面在角通量密度分布光滑的區域，采用較粗的角度離散仍能產生精確的計算結果。自適應方法不僅可有效控制離散誤差，且極大減少了計算量。屏蔽計算問題的幾何模型劃分為不同的求積區域，1個區域內的所有網格采用相同的求積組，分別定義每個求積區域的求積組。自適應過程中還需要定義一些常數，包括第1次自適應前的迭代次數、兩次自適應間的迭代次數、最大自適應次數和自適應收斂準則等。在穩態輸運問題的計算中，角度自適應方法以初始求積組開始輸運掃描，所有求積區域采用相同的低階求積組。經歷若干次源迭代后，基于當前的數值解獲得角度離散誤差分布。在此過程中需準確估計誤差分布，將其中一部分誤差相對較大的角度離散區域細化，即采用更高階求積組代替當前的低階求積組，盡可能地減少離散角度未知量的個數。然后，將該細化的求積組作為新的計算參數，在下一次自適應前一直使用。每經歷多次迭代后進行1次自適應判斷，自適應過程一直持續到滿足規定的誤差收斂準則或達到最大迭代次數。角度自適應方法流程如圖3所示。其中Na為自適應過程對應的內迭代次數，為提前設置的1組常數，Np為第1次自適應前的內迭代次數，為提前確定的1個常數。

圖3 角度自適應方法流程圖Fig.3 Flow chart of angular adaptive algorithm

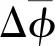
(1)

(2)

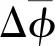
若求積區域邊界上任何一個網格的角度離散誤差大于事先規定的自適應細化收斂準則，則該求積區域的求積組細化到下一層高階求積組，同時更新該求積區域網格上的通量矩和區域邊界的出射角通量密度。自適應細化判斷如下：

(3)

(4)

式中：εflux為標通量密度自適應細化收斂準則；εcurrent為中子流密度自適應細化收斂準則。

通過當前數值求解的后驗誤差估計得到局部角度離散誤差，為角度自適應方法提供了判斷依據。角度自適應可采用4種尺度，包括全部求積區域統一自適應、各求積區域獨立自適應、各求積區域的每個卦限獨立自適應和各求積區域每個球面四邊形獨立自適應。另外，由于輸運方程空間角度的強耦合性，空間變量的離散方式和空間網格劃分都會對角度自適應過程產生影響。相鄰求積區域如果具有相同的離散求積點，一對一的簡單映射可傳遞相鄰求積區域的角通量密度。若相鄰求積區域的離散求積點存在不同的離散方向數目和不同的離散方向位置，簡單一對一的映射無法處理，角通量密度在一個求積區域傳遞到另一個求積區域需要映射方法。對于角通量密度從高階求積組映射到低階求積組的情況，一般采用多項式權重法，即通過4個與待求方向大圓距離最近的高階求積組的離散點，計算1個低階求積組離散點的角通量密度；對于從低階求積組映射到高階求積組的情況，則采用球諧函數擬合法，將角通量密度球諧函數展開并進行傳遞。

基于后驗誤差估計的角度自適應方法能自動優化角度離散，同時有效地控制全局通量密度的計算誤差，然而通常實際工程計算中感興趣的物理參數由局部或全局通量密度函數的積分確定，如核反應堆設計中功率密度分布、泄漏率和有效增殖因數等，輻射屏蔽計算中劑量當量率和探測器響應等，醫學物理應用中特定器官的劑量率等。從工程角度出發，獲得所有網格的精確解并沒有必要。在某些屏蔽計算問題中，數值結果在整個模型內相差多個數量級，在某區域的絕對誤差可能很小，但相對誤差可能會很大。在源區和源區與屏蔽材料的交界面處數值結果較大，自適應方法容易使該區域變量的離散過于細化，造成關注的屏蔽區域相對誤差依然很大。因此，關于特定物理量的誤差估計與現實應用更加相關，根據用戶的定義確定目標導向自適應方法中的目標函數，同時作為輸運共軛方程的源項，產生相對于目標函數的誤差估計。

3 理論方法測試與分析

圖4 Kobayashi基準題模型2Fig.4 Model 2 of Kobayashi benchmark

Kobayashi基準題模型2的幾何如圖4所示，該基準題模型對傳統確定論輸運方法提出了挑戰，是典型的深穿透屏蔽問題[15]。孔道的存在增加了角通量密度的各向異性程度，采用低階求積組時，導致較大的角度離散誤差。本文分析角度自適應方法的精度和效率，并研究關鍵參數的選擇對自適應方法的影響。

圖5示出均勻細化、角度自適應和目標導向自適應方法關鍵點相對誤差均方根的變化。由圖5可見，隨離散角度數的增多，相對誤差逐漸減小。角度自適應過程中，由于映射方法精度的影響會造成曲線在某些區域產生震蕩。在滿足精度要求的前提下，角度自適應和目標導向自適應方法均能有效地減少角度變量的數目。目標導向自適應方法僅采用52個卦限平均離散角度數就可獲得較高的計算精度。當所需精度均方根為1.00×10-2時，角度自適應方法需要的每個卦限平均離散角度數約為250個，而均勻細化方法的要超過3 000個。目標導向自適應方法僅是均勻細化方法離散角度數的1/60，極大地減少了計算量。角度自適應和目標導向自適應方法的計算時間分別為354 s和83 s。目標函數作為輸運共軛方程的源項，局部角度離散誤差通過對計算目標函數的重要性加權，產生適當的目標導向的誤差估計，生成針對特定目標函數精度改善最有效的離散角度分布。二階均勻細化求積組和目標導向自適應方法的相對誤差列于表1，二階均勻細化求積組的平均卦限離散方向數為48個，目標導向自適應方法僅增加了4個離散角度，計算精度獲得很大提高，相對誤差的均方根從1.86×10-1下降到1.19×10-2。

圖5 模型2關鍵點相對誤差的均方根變化Fig.5 RMS variation of relative error of key point in model 2

表1 模型2關鍵點通量密度的相對誤差Table 1 Relative error of key point of flux density for model 2

4 結論與展望

基于價值理論的目標導向方法與角度自適應相結合，有效地減弱了角度離散誤差對屏蔽計算的影響，提高了屏蔽計算方法的精度和效率。自適應求積組具有較好的收斂性，積分精度滿足輸運計算的要求。對于Kobayashi基準題模型，自適應方法比均勻細化離散角度數少1～2個數量級獲得了相同的計算精度，極大地減少了計算量。為進一步提高數值積分效率和精度，研究間斷有限元自適應離散求積組。空間和角度耦合的自適應方法研究是未來的一個難點，其中后驗誤差估計是極具挑戰的問題。