十字形圓鋼管-橫向板相貫節點的抗彎剛度

(1.浙江工業大學 建筑工程學院，浙江 杭州 310023；2.浙江工業大學 國際學院，浙江 杭州 310023)

圓鋼管構件具有雙向抗彎和抗扭性能優異、建筑視覺效果美觀、連接構造用鋼量省等眾多優點，因此鋼管相貫節點被廣泛應用于各種建筑結構。但當支管直徑較大且數量較多時，鋼管相貫節點將形成搭接連接，使得隱蔽焊縫質量難以保障，進而導致受力性能受到影響，而鋼管-板節點可以避免這個缺陷。此外，節點板還可連接索，形成剛柔混合體系，如鋼管拱+節點板+索+膜組成的大跨空間結構等。鋼管-板相貫節點按照節點板和鋼管的相對位置主要分為鋼管-縱向板節點、鋼管-橫向板節點和鋼管-斜板節點[1]。目前，關于鋼管-板節點的研究大多為節點靜力承載力方面[1-6]，但鋼管-板相貫節點的構造特點使其產生明顯的局部變形，表現出典型的半剛性特性[7]，節點的剛度將直接影響到結構的受力性能[8-10]。目前對于鋼管-板節點抗彎剛度的研究較少且集中在鋼管-縱向板節點[11]，鋼管-橫向板節點剛度的研究則集中在軸向剛度和半剛性性能方面[12-13]。在空間結構中應用較多的十字形節點圓鋼管-橫向板往往處于軸力、彎矩和剪力共同作用的復雜受力狀態，需要研究其抗彎剛度。

筆者通過有限元分析了十字形圓鋼管-橫向板相貫節點在彎矩作用下的傳力與局部變形特點，結合有限元參數分析和多元回歸分析，建立較實用的圓鋼管-橫向板相貫節點抗彎剛度參數化計算式，并將其與有限元結果進行對比，驗證其合理性。

1 節點的傳力方式和局部變形特點

筆者以有限元為研究手段，首先對十字形圓鋼管-橫向板節點在彎矩作用下的傳力方式、局部變形特點進行分析。節點有限元模型采用對稱面施加對稱約束的半結構，以減少計算量。主管兩端固定支座，用Coupling約束將板端部截面和其形心點(控制點)的各自由度耦合在一起，再在控制點上施加集中彎矩，有限元模型中材料彈性模量E=206 GPa，幾何參數為D=300 mm，βp=0.75，γ=15，τp=0.8，主管長LD取10D，支管凈長ld=l-D/2為3b，采用ABAQUS的六面體線性縮減積分單元C3D8R，網格劃分時主管沿壁厚方向為4等分，節點域內(中間2D范圍內主管)單元的最長邊和最短邊之比限制在2以內，橫向板沿厚度方向為2等分。節點構造與加載簡圖、網格劃分后的節點有限元模型見圖1。

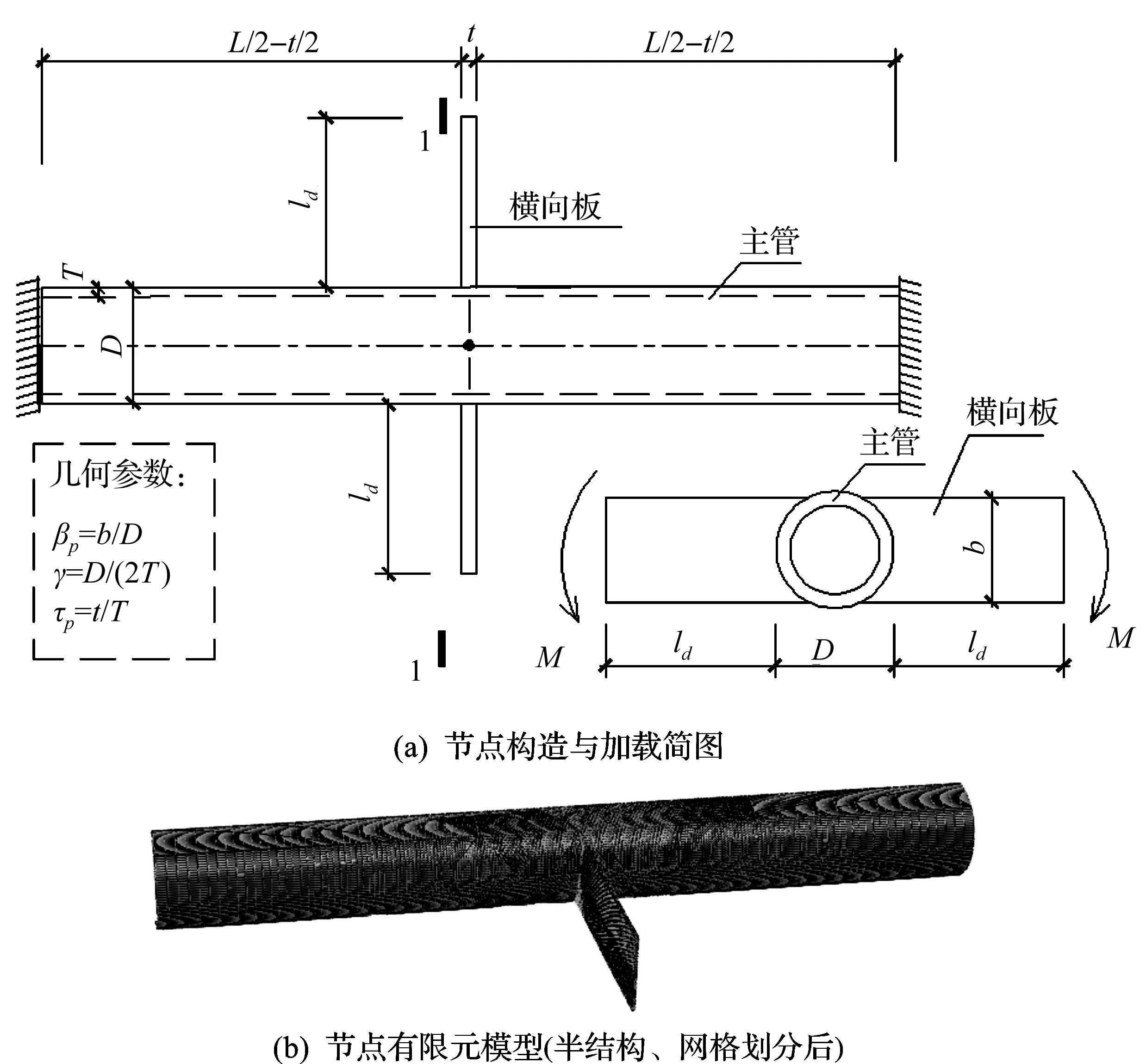
圖1 十字形節點的簡圖、有限元模型Fig.1 Structure diagram and FE model (with half structure) of cross-type transverse plate-to-CHS joint

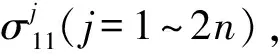
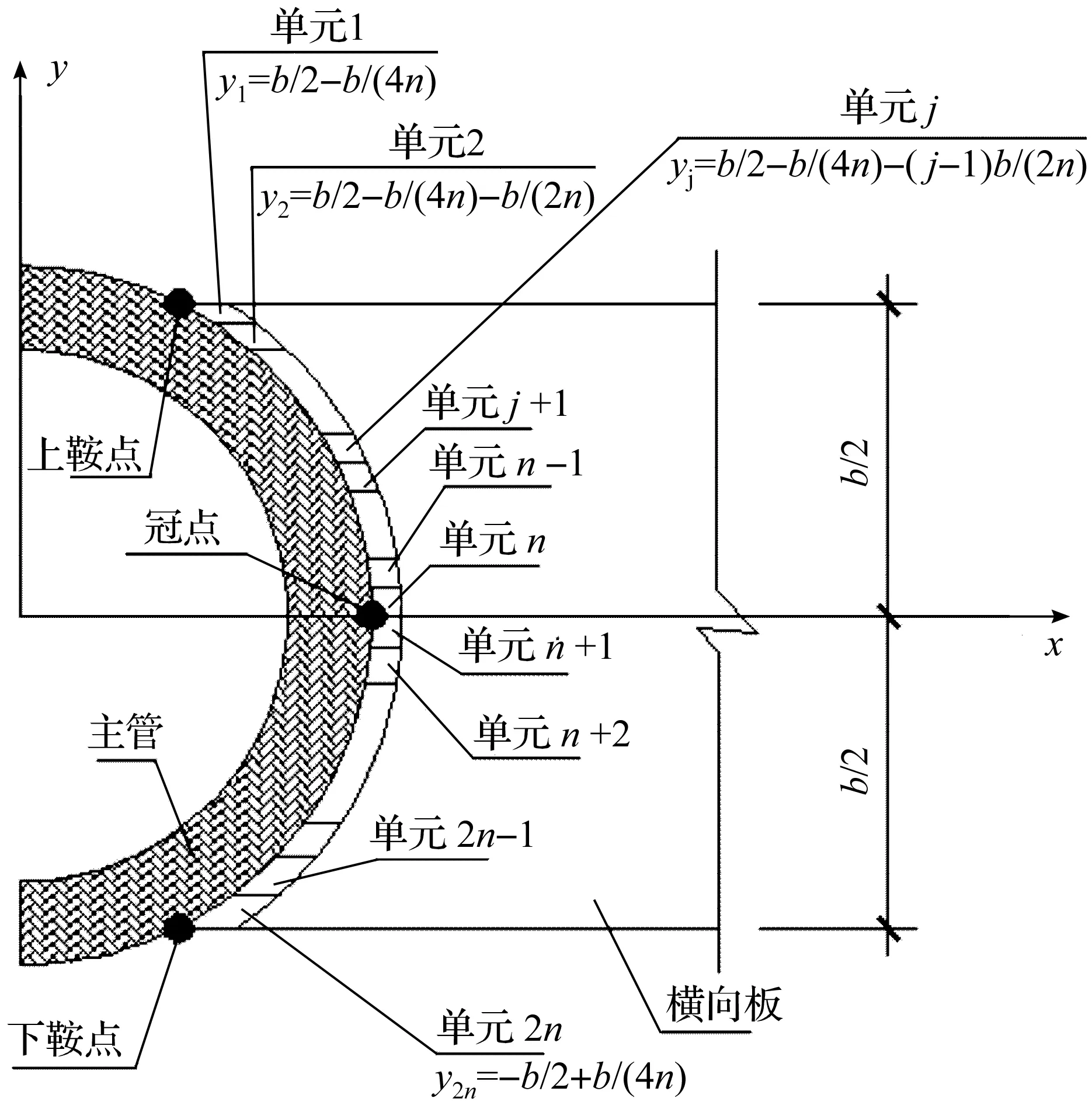
圖2 靠近相貫線的橫向板的一排單元的序號及位置Fig.2 Numerical order and location along the direction of plane width for every element of transverse plate near to intersecting line

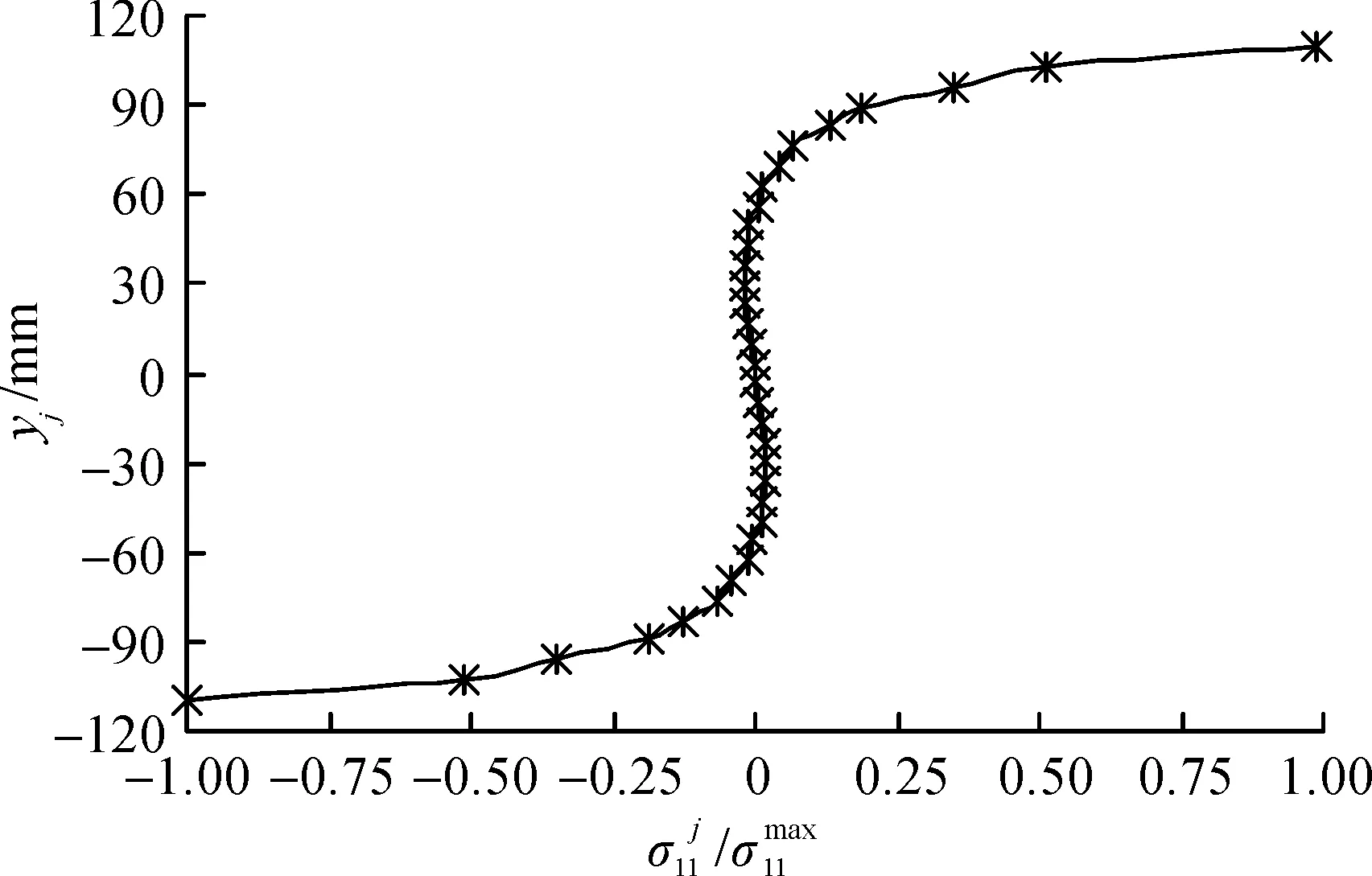
圖3 圓鋼管-橫向板節點(半結構)的彈性應力分布Fig.3 Elastic stress distribution of cross-type transverse plate-to-CHS joint (half structure) under bending moment

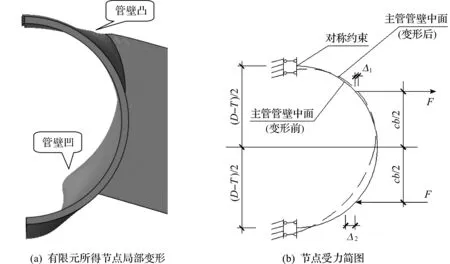
圖4 彎矩作用下節點(半結構)的局部變形和受力簡圖Fig.4 Local deformation from the result of FEA and the force diagram for the joints (half structure) under moment

2 節點抗彎剛度的影響因素分析

2.1 節點抗彎剛度的獲取

節點剛度定義為產生單位廣義位移所需的廣義力，圓鋼管-橫向板的抗彎剛度K定義為

(1)

式中：M為橫向板傳來的彎矩(廣義力)，即為節點有限元模型中的板端部截面控制點上的集中力矩；節點轉角θ計算公式為

(2)

式中：ld為支管凈長(圖1)；δrp為節點轉動(相貫線附近的主管管壁凹凸變形所致)導致橫向板產生的近似剛體位移，利用板端面加載點(控制點)的總變形δtot(節點有限元計算得到)扣除δbp(橫向板作為桿件產生的彎曲撓度)得到；δbp可利用有限元實體單元建立，如圖5所示的固定端為圓柱面的懸臂梁模型獲得，也可用簡單彈性梁(跨度為ld的等截面固定支座梁、截面高×寬為b×t)理論計算得到，對比βp=0.45，0.75，0.9，γ=10，15，22等幾個節點表明，兩種方法所得δbp的差異在10%以內，故采用彈性梁理論計算δbp，以減少計算量。

圖5 懸臂梁有限元模型Fig.5 FEA model of cantilever beam

2.2 節點抗彎剛度的影響因素分析

十字形圓鋼管-橫向板相貫節點的幾何參數包括了D，βp，γ，τp，這些參數都有可能影響節點抗彎剛度。首先建立節點有限元模型(單元類型、邊界約束條件等與第1部分所述一致)進行分析計算，獲得大量的節點抗彎剛度數據，對可能影響節點剛度的因素進行單參數分析，了解其對節點剛度的影響。表1給出節點抗彎剛度K關于D的單參數分析結果，其余節點幾何參數為γ=15，βp=0.75，τp=0.8，文中鋼材的材料彈性模量為E=206 GPa。表中的誤差指各個節點的KD-3最大值與最小值之間的相對誤差。由表1可知：誤差約2.2%，可認為K與D3成正比關系。對參數E(20～2 000 GPa)進行類似分析，結果KE-1的相對誤差小于1%，說明K與E成正比關系。K與ED3成正比，不僅可以用量綱關系來解釋，還可通過圖4(b)所示的節點受力簡圖(對稱約束的拱模型)來解釋，借鑒Togo關于X形圓鋼管相貫節點在支管軸力作用下的承載力計算的環模型思想[14]，將圖4(b)中的力F均勻布在拱的截面寬度ηD上，因此圖4(b)所示拱模型的抗彎剛度EI=ηET3D/12，節點轉角θ近似為(Δ1-Δ2)/(cb)，再根據桿系結構力學以及節點抗彎剛度的定義，經推導得節點抗彎剛度為

(3)

表1 節點剛度關于D的單參數分析結果及其誤差Table 1 Parametric analysis for D and its error

圖6給出了十字形圓鋼管-橫向板相貫節點抗彎剛度K關于γ(βp=0.6，τp=0.8)，βp(γ=15，tp=0.8)，τp(βp=0.75，γ=15)的單參數分析結果，D均取300 mm，圖6中橫坐標為節點幾何參數γ等，縱坐標為節點剛度的無量綱化KE-1D-3×104，圖6中的粗線為根據有限元所得散點數據的擬合結果。由圖6可看出：K與γ，βp分別呈近似的冪函數、指數函數關系，對比之下，函數γ-n能很好地表達K—γ曲線，但簡單的指數函數exp(c0βp)表達K—βp曲線時有一定的差異，尤其βp較大時。K隨參數τp(0.3～1.2)的增加而呈近似線性增加，但其中K的最大值與最小值之間的差異僅約為11%，故可忽略τp對K的影響。

圖6 參數γ，βp，tp對節點抗彎剛度的影響Fig.6 Effect of parameters γ，βp，τp on flexural rigidity of cross-type transverse plate-to-CHS joint

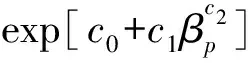
在前面γ與βp變化的20 個節點有限元模型的基礎上，增加τp=0.4，1.2，形成共計60 個節點有限元模型并計算得到60 個節點剛度，較全面地分析τp對節點剛度的影響，見圖7。圖7中的差異1，2分別表示τp=0.4，τp=1.2時的節點剛度與τp=0.8的節點剛度之間的相對差異。由圖7可知：差異1，2大多在5%以內，即使是τp=0.4的節點剛度K與τp=1.2的K之間的相對差異也大多小于10%，進一步說明τp十字形圓鋼管-橫向板節點抗彎剛度的影響小，可忽略。

圖7 τp對節點抗彎剛度的影響Fig.7 Effect of τp on flexural rigidity of the joints

3 節點剛度參數化計算公式的建立與校驗

基于單參數分析的結果，十字形圓鋼管-橫向板相貫節點的彈性抗彎剛度計算式為

(4)

式中C0～C3為常系數。

根據前面計算得到的60 個節點抗彎剛度散點數據，通過置信度為95%的多元非線性回歸分析，常系數為C0～C6，最終得到十字形圓鋼管-橫向板相貫節點剛度剛度參數化計算式為

(5)

利用前面有限元計算所得的69 個節點有限元模型計算所得剛度數據(包含單參數分析數據在內)，同時新增基于三參數三水平正交設計所得的9 個節點有限元模型(模型參數取值見表2)計算所得的剛度數據，用來校驗節點抗彎剛度參數化計算式(5)的合理性。節點模型涉及參數范圍為D(100～500 mm)，τp(0.3～1.2)，βp(0.3～0.9)，γ(7～30)，基本上覆蓋工程常用范圍。圖8比較了有限元計算結果和式(5)計算值，圖8中的誤差值=(計算值-有限元值)/有限元值×100%。由圖8可知：誤差大部分都在10%以內，少量誤差為10%～20%，最大誤差約21%，誤差絕對值的平均值約6%。因此，兩側橫向板在同向相等彎矩(工程中最常見荷載工況)作用下，十字形圓鋼管-橫向板節點的彈性剛度參數化計算式總體上較好地反映了節點的抗彎半剛性。

表2 三參數三水平正交模型表格

Table 2 Orthogonal model table for three parameters and three horizontal

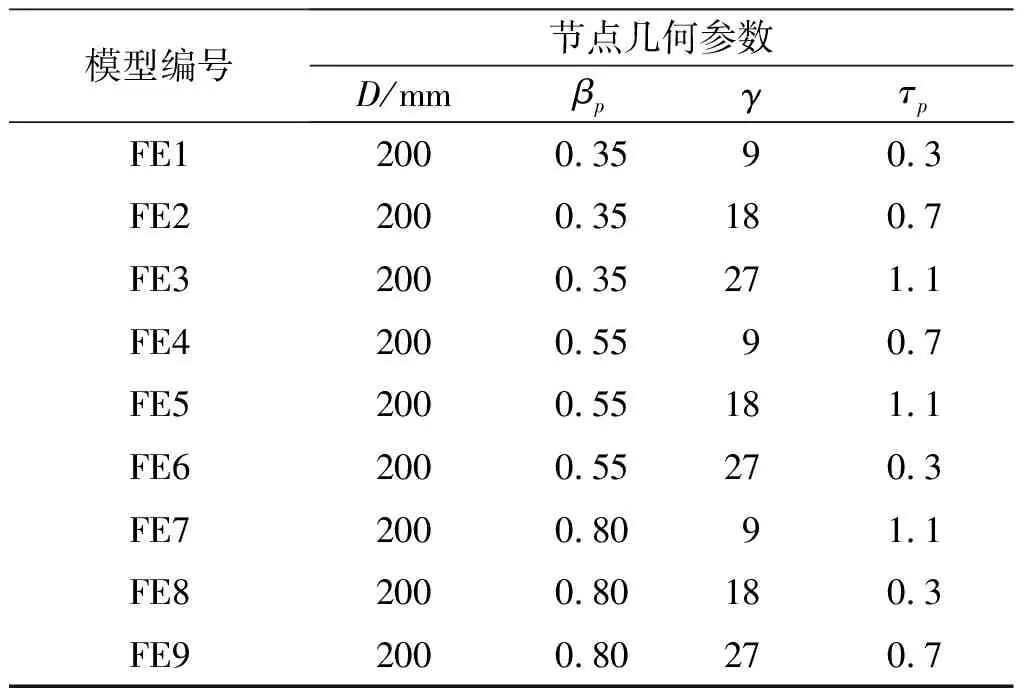
模型編號節點幾何參數D/mmβpγτpFE12000.3590.3FE22000.35180.7FE32000.35271.1FE42000.5590.7FE52000.55181.1FE62000.55270.3FE72000.8091.1FE82000.80180.3FE92000.80270.7

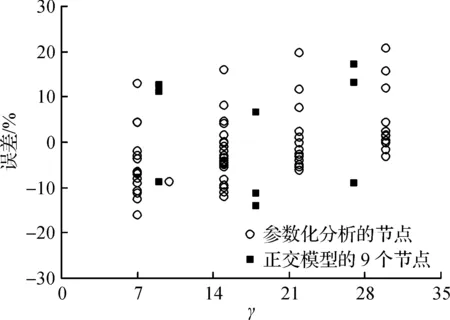
圖8 式(5)計算值與有限元結果的誤差Fig.8 Error for the elastic flexural rigidity of cross-type transverse plate-to-CHS joints between Eq. 5 and FEA shaped-type joints with the change of βp and γ

4 結 論

基于十字形圓鋼管-橫向板相貫節點在彎矩作用下的傳力和局部變形特點，結合有限元單參數分析和多元非線性回歸分析，獲得較實用的十字形節點抗彎彈性剛度計算式，研究獲得以下結論：1) 相貫線附近的板的軸向應力從鞍點沿冠點急劇下降，橫向板的傳來的彎矩可簡化為一對作用在上、下鞍點附近的力偶；2) 節點抗彎剛度K與ED3成正比，與βp，γ呈近似的指數函數、冪函數關系，βp和γ對K的影響大，而對τp的影響小；3) 有限元結果及已有試驗數據驗證了節點抗彎剛度參數化計算式在0.3≤βp≤0.9，7≤γ≤30，0.3≤τ≤1.2，100 mm≤D≤500 mm這一工程常見幾何參數范圍內使用的合理性。