多地面運動目標大動態(tài)SAR成像稀疏表示

楊 磊，岳云澤，李埔丞，章 濤，楊 桓

(1.中國民航大學 天津市智能信號處理與圖像處理重點實驗室，天津 300300；2.中國工程物理研究院 電子工程研究所，四川 綿陽 621999)

合成孔徑雷達(Synthetic Aperture Radar，SAR)具有全天時、全天候的工作能力，可對地面靜止場景/目標實現(xiàn)高分辨率成像[1]。合成孔徑雷達地面運動目標指示(Ground Moving Target Indication，GMTI)可進一步實現(xiàn)在復(fù)雜地面雜波環(huán)境下對運動目標的檢測、估計和定位[2]。通過引入沿航向多通道天線，可以大大地減輕地面靜止場景雜波對運動目標檢測的影響，從而便于估計運動目標的多普勒信息，實現(xiàn)對目標速度的估計和重新定位。隨著現(xiàn)代雷達成像技術(shù)對成像分辨率需求的不斷升高，運動目標造成的圖像散焦問題愈加嚴重，由此發(fā)展起來的地面運動目標成像(Ground Moving Target Imaging，GMTIm)技術(shù)研究愈加火熱。然而，對于復(fù)雜的多地面運動目標場景，獲得聚焦性能良好的多目標合成孔徑雷達圖像仍然問題較多。

為了實現(xiàn)對多地面運動目標的同時聚焦成像，傳統(tǒng)的方法通常通過一系列的目標運動參數(shù)假設(shè)建立匹配濾波器組，分別實現(xiàn)對運動目標的合成孔徑雷達成像，并從中選取最佳的聚焦參數(shù)，從而獲得目標參數(shù)估計和成像結(jié)果[3]。匹配濾波器組法雖然操作簡單，但是匹配濾波器的維度隨著運動目標數(shù)目的增加劇增，導(dǎo)致實用性驟減。由此，后續(xù)提出了基于時頻分析的運動目標估計方法，可以避免建立超完備字典，從而直接獲得目標運動參數(shù)估計并建立匹配濾波器實現(xiàn)聚焦成像。其中WVD (Wigner-Ville Distribution)時頻分析方法運算效率較高，但是對于多目標情況存在嚴重的交叉項問題[4]。分數(shù)傅里葉變換(Fractional Fourier Transform，F(xiàn)rFT)作為一種線性時頻表示方法，可以避免交叉項的影響，但是時頻表示動態(tài)范圍偏低[5]。此外，即使在獲得目標參數(shù)估計的情況下，匹配濾波法作為一種典型的傅里葉頻譜分析方法，雖然計算相對簡單，但是在多目標場景下成像響應(yīng)的動態(tài)范圍偏低，響應(yīng)旁瓣過高，尤其在目標相距較近或者在同一距離單元內(nèi)時，運動目標的散焦響應(yīng)或高旁瓣可能導(dǎo)致目標難以被準確檢測，甚至造成虛假目標。

2006年DONOHO正式提出了“壓縮感知”的概念[6]，并給出稀疏信號可恢復(fù)的重要條件之一是感知字典滿足有限等距特性(Restricted Isometry Property，RIP)。為了能夠量化評估有限等距特性，文獻[7]中定義了壓縮感知字典的互相關(guān)度，并通過實驗驗證了傅里葉稀疏表示字典互相關(guān)度越小，越能以高概率滿足有限等距特性，從而可以實現(xiàn)對稀疏合成孔徑雷達圖像的恢復(fù)。經(jīng)過近十年的快速發(fā)展，目前針對合成孔徑雷達成像稀疏恢復(fù)的算法大致可以分為3類：貪婪類算法、凸優(yōu)化類算法和統(tǒng)計學習類算法。由于概率先驗的引入和統(tǒng)計學習的優(yōu)勢，相較其他兩類算法，統(tǒng)計學習類算法不但精度較高，而且模型可擴展性也較強，通過引入具有稀疏特征的先驗概率分布，可以獲得目標合成孔徑雷達圖像的后驗概率分布估計。

針對多地面運動目標同時合成孔徑雷達成像時存在的響應(yīng)動態(tài)范圍偏低的問題，筆者提出了一種基于稀疏貝葉斯學習的大動態(tài)合成孔徑雷達成像稀疏表示方法。該方法首先利用漸進線性的呂氏分布[8](LV’s Distribution, LVD)時頻表示方法獲得多個地面運動目標的參數(shù)估計，可以保證在較長相干積累時間內(nèi)交叉項的影響可以忽略不計；然后，利用估計獲得的目標參數(shù)建立參數(shù)化的二階多項式傅里葉字典，同時應(yīng)用μt互相關(guān)度計算方法定量評估該字典的有限等距特性性能；最后，針對擬引入的稀疏拉普拉斯先驗分布與觀測數(shù)據(jù)概率分布非共軛的問題，進行層級貝葉斯建模，同時考慮目標高階運動及載機運動誤差造成的相位誤差影響，應(yīng)用基于變分貝葉斯的期望最大算法求解目標后驗概率密度函數(shù)，從而獲得響應(yīng)動態(tài)范圍較大且聚焦性能良好的多運動目標合成孔徑雷達圖像。仿真數(shù)據(jù)及權(quán)威的實測Gotcha數(shù)據(jù)集驗證了筆者所提算法針對多地面運動目標大動態(tài)成像的處理性能。

1 SAR-GMTIm信號模型

為了保證地面運動目標的檢測和成像性能，采用多通道合成孔徑雷達體制實現(xiàn)對地面靜止場景回波的有效抑制[9]。多通道SAR-GMTIm幾何模型如圖1所示，其中機載合成孔徑雷達工作在聚束模式。假設(shè)載機以恒定速度v沿預(yù)定航線飛行，如圖1中虛線航線所示。

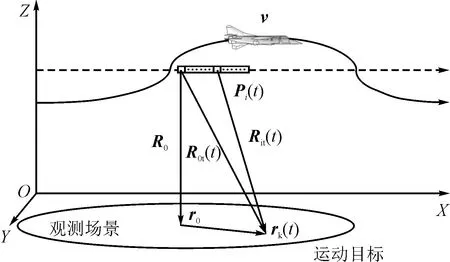
圖1 多通道SAR-GMTIm幾何模型示意圖

多通道合成孔徑雷達天線第i通道等效天線相位中心(Antenna Phase Center，APC)的位置可表示為Pi(t)=P0(t)+di=P0(t)+div/|v|，其中P0(t)表示參考通道，di表示第i通道與參考通道之間的距離矢量，di=|di|，t表示方位時間，且t∈[T0,T1]。再設(shè)地面運動目標運動軌跡rt(t)=R0+r0+vtt+att2/2，其中R0表示載機航線到場景中心的參考斜距，r0表示目標位置相對觀測場景中心的位置偏移，vt和at分別表示目標速度和加速度矢量。由此可得第i通道天線相位中心到目標的斜距矢量Rit(t)=rt(t)-Pi(t)。

接下來，針對各個通道天線相位中心運動目標的斜距矢量進行泰勒展開近似，同時考慮K個運動目標成像場景，經(jīng)過極坐標算法(Polar Format Algorithm，PFA)成像操作后，運動目標回波可近似建模為線性調(diào)頻信號形式(Linear Frequency Modulation，LFM)：

(1)

其中，sinc(·)表示距離向包絡(luò)形式，r表示距離向位置變量，t′表示經(jīng)過極坐標算法插值處理后的方位時間變量。根據(jù)文獻[10]可知，krt=k0t′，其中kr表示極坐標算法插值后距離向波數(shù)變量，k0(k0=4π/λ)表示波數(shù)中心，λ表示波長。根據(jù)文獻[10]中的推導(dǎo)，可得

(2)

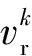
多通道合成孔徑雷達系統(tǒng)每個通道接收到的回波包括地面靜止場景回波(即雜波)，以及地面運動目標回波和通道噪聲。在忽略通道間幅相誤差的情況下[11]，第i條通道接收到的回波相比參考通道存在延時Δηi=di/v。根據(jù)地面靜止目標回波方位不變性[12]，各個通道之間雜波可以認為是相同的。而對于地面運動目標回波，由于在延時Δηi過程中存在目標運動移位，因此動目標回波在通道間存在差異。應(yīng)用偏置天線相位中心(Displaced Phase Center Antenna，DPCA)[13]技術(shù)，可通過簡單的通道間回波相減實現(xiàn)對雜波的對消。經(jīng)過雜波對消后的回波信號可近似表示為

(3)

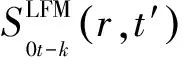
(4)

其中，ΔT表示信號相干積累時間。由式(4)可見，ΔT越大，針對多普勒中心頻率和多普勒調(diào)頻率的表示精度越高，并且多目標交叉項的影響越小[8]。但ΔT越大，運動目標的運動狀態(tài)就越復(fù)雜，完成距離徙動校正的難度就越大。因此在對實際問題的處理中，需要選擇一個合適的信號相干積累時間ΔT，既要保證距離徙動校正的便捷性，又要保證呂氏分布對多普勒參數(shù)的估計精度。

此時，多地面運動目標在雜波抑制后的回波信號可進一步簡化表示成矩陣形式：

Y=EAX+CN，

(5)

其中，Y為觀測數(shù)據(jù)矩陣，即經(jīng)過雜波抑制后的距離多普勒域數(shù)據(jù)，如式(3)所示，距離向按列排布，方位向按行排布；X為待求解的合成孔徑雷達運動目標圖像矩陣；E為乘性的相位誤差矩陣，根據(jù)該相位誤差的非空變特性，可建模為對角矩陣，對角線上的元素對應(yīng)相應(yīng)方位時刻的相位誤差Δφ(t′)；CN表示剩余的雜波和系統(tǒng)噪聲；A為成像表示字典。根據(jù)呂氏分布時頻表示獲得的多普勒參數(shù)，可將A建模為

(6)

2 基于參數(shù)化稀疏貝葉斯學習的SAR-GMTIm算法

基于以上敘述建立的SAR-GMTIm回波信號模型如式(5)所示。為了獲得目標合成孔徑雷達圖像X，可直接利用X=A-1Y，該方法可以被理解為是一種匹配濾波方法。在存在多個目標同時成像的場景中，應(yīng)用該方法獲得的圖像的目標響應(yīng)的動態(tài)范圍會受到嚴重影響，造成旁瓣升高，甚至導(dǎo)致假目標的出現(xiàn)。此外，受到加性觀測噪聲和乘性相位誤差的影響，匹配濾波方法會出現(xiàn)嚴重失配的現(xiàn)象，造成成像性能損失嚴重。針對該問題，筆者擬應(yīng)用基于統(tǒng)計機器學習理論的貝葉斯估計算法，對目標合成孔徑雷達圖像X的后驗概率密度函數(shù)進行估計，相應(yīng)的數(shù)學期望即為所求的合成孔徑雷達圖像。

2.1 層級貝葉斯概率模型

假設(shè)式(7)中的加性誤差CN服從均值為零的對稱復(fù)高斯分布，由此可得觀測數(shù)據(jù)似然函數(shù)為

(7)

其中，β=[β1,…,βM]，βm表示第m個距離單元的加性誤差精度參數(shù)，對應(yīng)高斯模型中方差的倒數(shù)。為了實現(xiàn)對運動目標合成孔徑雷達圖像X的后驗概率密度函數(shù)估計，需要對X施以合適的先驗假設(shè)。基于雜波抑制后運動目標存在稀疏性的先驗知識，筆者擬對X引入稀疏先驗分布。通常情況下，稀疏先驗分布屬于重尾分布，如拉普拉斯(Laplace)分布、學生t(Student-t)分布等。筆者采用拉普拉斯分布作為稀疏先驗概率分布。然而，考慮到拉普拉斯先驗分布與式(7)相應(yīng)的觀測數(shù)據(jù)高斯概率分布非共軛，將導(dǎo)致X的后驗概率密度函數(shù)無閉合解，故針對拉普拉斯分布建立層級貝葉斯模型，通過引入中間超參數(shù)分層建立概率模型。在層級貝葉斯概率模型中，第1層首先對動目標合成孔徑雷達圖像建立多變量聯(lián)合高斯分布

(8)

其中，Λm=diag(α：m)，可以看成是超參數(shù)矩陣α中第m列構(gòu)成的對角矩陣，該矩陣表示式(8)所示高斯分布的協(xié)方差矩陣。然后，第2層引入關(guān)于α的條件概率分布服從參數(shù)為η和λ的伽馬分布:

(9)

(10)

其中a，b，c，d可設(shè)置為常參數(shù)[10]，根據(jù)經(jīng)驗值可取10-6。

2.2 基于變分貝葉斯的期望最大算法

根據(jù)2.1節(jié)給出的層級貝葉斯建模結(jié)果，直接應(yīng)用貝葉斯推論計算合成孔徑雷達圖像X和超參數(shù)α，λ，β的聯(lián)合后驗概率密度函數(shù)為

(11)

令Θ={X,α,λ,β}，據(jù)變分貝葉斯原理[14]，采用平均場假設(shè)進行因式分解近似，并進一步代入聯(lián)合似然函數(shù)，可得相應(yīng)隨機變量Θi的解為

(12)

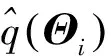
(13)

將式(7)～(8)代入式(12)，可得[10]

(14)

其中,

(15)

由式(14)～(15)可見，動目標合成孔徑雷達圖像的后驗概率密度函數(shù)估計服從復(fù)高斯分布，對應(yīng)的期望μ可用來表示X的均值，對應(yīng)的方差Σm可用來表示X第m個距離單元的協(xié)方差矩陣。同理，根據(jù)式(12)可得超參數(shù)α的后驗概率密度函數(shù)估計，并將式(8)～(9)代入，可得αnm的第l階矩為

(16)

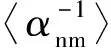
(17)

其中，超參數(shù)λ的后驗概率密度函數(shù)估計服從伽馬分布。最后，再由式(14)可得超參數(shù)β的后驗概率密度函數(shù)估計，并將式(7)～(10)代入，可得超參數(shù)βm的均值為

(18)

其中，‖·‖F(xiàn)表示矩陣的F范數(shù)。由式(18)可見，超參數(shù)β的后驗概率密度函數(shù)估計服從伽馬分布。通過式(17)～(20)的循環(huán)迭代，可以獲得各個隨機變量的均值估計。由于在迭代中體現(xiàn)了隨機變量的相關(guān)制約關(guān)系，從而可以有效降低誤差的傳播效應(yīng)。

在獲得隨機變量Θ的后驗概率密度函數(shù)估計后，乘性相位誤差E的估計值可通過下式計算[10]：

(19)

由于目標函數(shù)為凸函數(shù)，通過分別對E對角線上元素的實部和虛部計算偏導(dǎo)并置零，計算相位誤差的解為

(20)

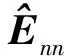
筆者在利用合成孔徑雷達圖像相對于背景固有的稀疏性的基礎(chǔ)上，引入X的稀疏先驗分布。針對X的稀疏先驗分布與觀測數(shù)據(jù)所服從的高斯分布不共軛的問題，引入層級貝葉斯概率模型。在層級貝葉斯概率模型的求解中，利用基于變分貝葉斯的最大期望方法，完成了對隨機變量Θ={X,α,λ,β}以及乘性相位誤差E的后驗概率密度函數(shù)的貝葉斯估計。

3 二階多項式傅里葉字典A的RIP特性定量評估

上面討論了針對SAR-GMTIm回波信號模型，應(yīng)用參數(shù)化貝葉斯估計方法實現(xiàn)了多地面運動目標的大動態(tài)范圍合成孔徑雷達成像和稀疏特征增強。根據(jù)稀疏恢復(fù)理論[7]，針對雜波抑制后運動目標的稀疏性特征，筆者引入拉普拉斯先驗分布，并應(yīng)用呂氏分布時頻表示獲得參數(shù)化的壓縮感知表示字典A。為了進一步評估引入的參數(shù)化字典在稀疏恢復(fù)中的性能，明確應(yīng)用低維度回波信號恢復(fù)高分辨圖像的壓縮感知性能，研究應(yīng)用互相關(guān)度對稀疏感知字典A的性能進行定量評估。

在壓縮感知理論中，判斷傳遞字典是否可以成為壓縮感知傳遞矩陣的一個重要的標準是有限等距特性[7]。若存在δs∈(0,1)，使得二階多項式傅里葉字典A的子矩陣As∈CN×s和對應(yīng)的X滿足

(21)

則稱二階多項式傅里葉字典A∈CN×KN以有限等距常數(shù)δs滿足s階有限等距特性，其中1≤s≤KN且s為整數(shù)。有限等距性質(zhì)常數(shù)(Restricted Isometry Property Constant, RIPC)δK為所有可能的δs的下確界，滿足

(22)

觀察式(21)～(22)可見，實際應(yīng)用中很難定量計算δK，因此筆者引入互相關(guān)度的定義來從側(cè)面定量評估該二階多項式傅里葉字典的性能。二階多項式傅里葉字典A的互相關(guān)度定義為

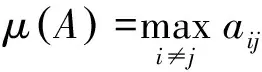
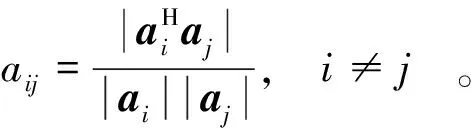
(23)

aij代表二階多項式傅里葉字典A的不同的兩列ai，aj的相關(guān)系數(shù)。在不同空間位置的回波響應(yīng)之間，二階多項式傅里葉字典A的互相關(guān)度度量了多個地面運動目標最保守情況下的相關(guān)性。

由于同時對多個地面運動目標成像時，前面提出的二階多項式傅里葉字典A的有限等距特性必然不會十分理想。由式(6)可見，由于B的引入造成了字典A中列之間的相關(guān)度升高，嚴重影響了稀疏信號恢復(fù)的性能，因此A的本身結(jié)構(gòu)所造成的互相關(guān)度較高的問題會影響壓縮感知的性能。為此，筆者為μ的衡量設(shè)定一個門限值t，取出互相關(guān)度位于前t的列集合，然后求其平均互相關(guān)度。由于相關(guān)性與稀疏信號重構(gòu)性能直接相關(guān)，平均互相關(guān)度可以作為一種衡量稀疏驅(qū)動合成孔徑雷達重構(gòu)的平均重構(gòu)性能的方法。對A來說，μt被定義為互相關(guān)度位于前t的不同列之間的互相關(guān)度所有歸一化內(nèi)積的平均值，記為

(24)

其中，εt表示包含互相關(guān)度位于前t的所有列的集合。由于設(shè)定了閾值，使得μt相對于μ對離群點具有更強的魯棒性，從而降低了這些離群點對A的互相關(guān)度的影響。同時，μt可以與文獻[15]中的累計相關(guān)度聯(lián)系起來，用以導(dǎo)出在凸代價函數(shù)條件下的稀疏信號恢復(fù)條件。此外，在實際應(yīng)用中，文獻[15]提出的累計相關(guān)決定了閾值t的上界。在實際的雷達數(shù)據(jù)收集之前，可以通過計算μt來確定需要設(shè)定的閾值，從而定量衡量二階多項式傅里葉字典的有限等距特性。

4 實驗驗證

4.1 仿真實驗

仿真數(shù)據(jù)模擬機載合成孔徑雷達工作在聚束模式，X波段，帶寬為75 MHz，脈沖重復(fù)頻率為1 000 Hz。合成孔徑雷達天線沿航向三通道，相鄰?fù)ǖ捞炀€相位中心間距為0.2 m，載機飛行速度約為150 m/s，成像場景距離機載合成孔徑雷達參考距離約為10 km，仿真數(shù)據(jù)相干處理時間約為2 s。仿真目標為3個點狀的地面運動目標，其中兩個點目標相距較近，另一個相距較遠。3個點目標的后向散射系數(shù)服從0.8～1.2的均勻分布，背景雜波設(shè)為均勻雜波，系統(tǒng)噪聲假設(shè)服從零均值的高斯分布，乘性相位誤差函數(shù)服從高斯分布。在仿真實驗過程中，對成像場景內(nèi)的動目標進行數(shù)據(jù)預(yù)處理，以保證越距離單元徙動有效校正。當分辨率要求不高時，對運動目標分別進行一階Keystone變換和二階Keystone變換以校正距離走動和距離彎曲信息。當相干積累時間較長或要求的分辨率提高時，其越距離單元走動、多普勒擴散、多普勒模糊使得完成校正的難度大大增加。傳統(tǒng)的Keystone變換處理無法實現(xiàn)更為良好的校正效果，此時校正方法可參考文獻[16]。

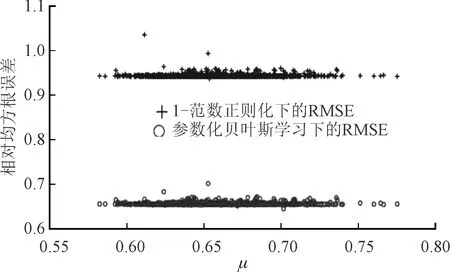
圖2 1 000次蒙特卡羅實驗下μ與相對均方根誤差的關(guān)系

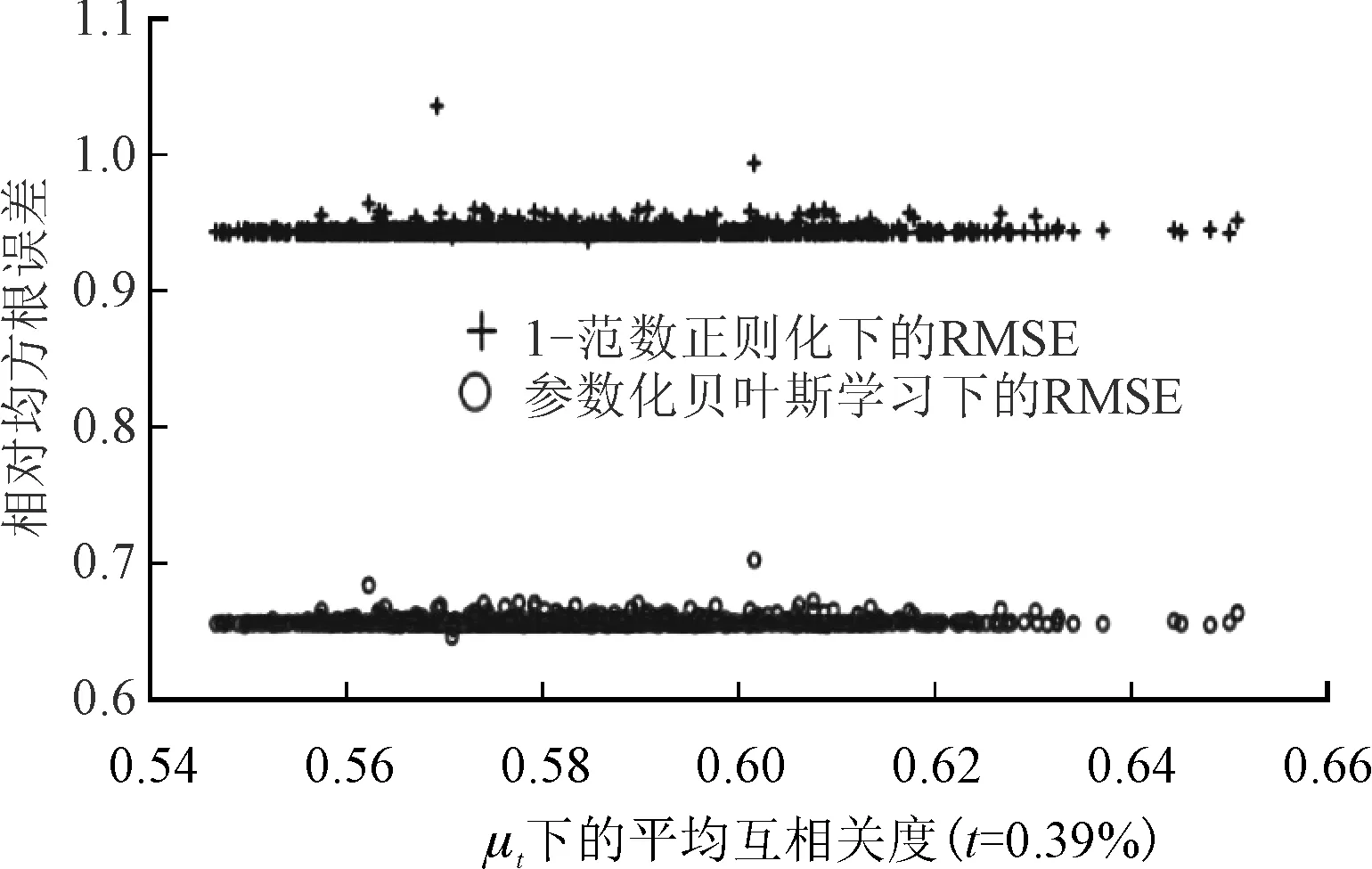
圖3 1 000次蒙特卡羅實驗下μt與相對均方根誤差的關(guān)系

考慮對雜波抑制后的地面運動目標回波數(shù)據(jù)進行隨機降采樣，再分別應(yīng)用參數(shù)化貝葉斯估計和傳統(tǒng)的1-范數(shù)正則化方法進行成像重構(gòu)，同時針對相應(yīng)降采樣后的二階多項式傅里葉字典A設(shè)定t=0.39%為閾值，并計算相應(yīng)的互相關(guān)度μ和μt，最后采用相對均方根誤差(Relative Mean Square Error，RMSE)計算重構(gòu)誤差[17]。經(jīng)過1 000次蒙特卡羅實驗并計算相應(yīng)的均值,可得如圖2所示的仿真結(jié)果。根據(jù)多次獨立同分布試驗的極限分布服從高斯分布，且滿足各態(tài)歷經(jīng)性，因此可以應(yīng)用幾何平均近似替代統(tǒng)計平均。

圖2和圖3分別給出了應(yīng)用筆者所提參數(shù)化貝葉斯估計及傳統(tǒng)1-范數(shù)正則化方法得到的μ和μt互相關(guān)度與成像重構(gòu)精度相對均方根誤差結(jié)果，其中1 000次蒙特卡羅實驗的結(jié)果以點狀分布在平面上。由圖可見，應(yīng)用參數(shù)化貝葉斯估計恢復(fù)的成像結(jié)果恢復(fù)精度遠高于應(yīng)用1-范數(shù)正則化恢復(fù)的成像結(jié)果，相應(yīng)的相對均方根誤差分布在約為0.65的平直線上，遠低于1-范數(shù)正則化方法獲得的相對均方根誤差約為0.95。此外，通過對比圖2和圖3可見，μt互相關(guān)度的結(jié)果相比μ的結(jié)果在橫軸方向上相對集中，因此應(yīng)用μt對稀疏表示字典進行有限等距特性評估更為穩(wěn)健可靠。

圖4所示為仿真實驗結(jié)果。其中圖4(a)為仿真實驗原始參考圖，其中包括3個仿真點運動目標。對回波數(shù)據(jù)進行降采樣率為0.5的降采樣并施加0 dB加性噪聲和隨機相位誤差，可得匹配濾波成像結(jié)果，如圖4(b)所示。由圖4可見，由于多目標同時成像，造成直接匹配濾波的結(jié)果點目標響應(yīng)動態(tài)范圍降低，此外，降采樣和噪聲及相位誤差的引入進一步降低了成像質(zhì)量。筆者應(yīng)用圖像熵值來衡量合成孔徑雷達成像結(jié)果的聚焦性能[18]，圖像熵值越小，則成像聚焦性能越好。應(yīng)用1-范數(shù)正則化方法進行稀疏恢復(fù)可得結(jié)果如圖4(c)所示，可見目標成像的響應(yīng)動態(tài)范圍得到了大幅度提升，目標聚焦性能明顯提升，圖像熵值相應(yīng)減小。最后，如圖4(d)所示，應(yīng)用筆者所提的基于參數(shù)化稀疏貝葉斯學習的多目標大動態(tài)成像方法，目標響應(yīng)的旁瓣可進一步降低，圖像聚焦性能進一步提升，熵值進一步下降。

圖4 一次蒙特卡羅實驗下的不同算法成像結(jié)果對比

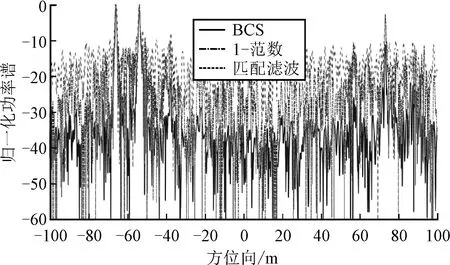
圖5 不同恢復(fù)算法間方位向響應(yīng)曲線比較(3個點目標的尖峰分別在方位向的-65.8，-53.5，74 m處)

為了進一步顯示稀疏恢復(fù)在大動態(tài)成像上的優(yōu)勢，圖5給出了圖4中響應(yīng)結(jié)果的方位向響應(yīng)曲線圖，其中虛線、點劃線和實線分別為直接匹配濾波、1-范數(shù)正則化和參數(shù)化貝葉斯估計結(jié)果。通過對比可見，合成孔徑雷達所提方法在提高多目標同時成像時的動態(tài)范圍較為明顯，效果相比傳統(tǒng)方法有明顯提升。

4.2 實測數(shù)據(jù)實驗

應(yīng)用多通道實測數(shù)據(jù)驗證參數(shù)化稀疏貝葉斯學習大動態(tài)成像算法的有效性和優(yōu)越性。實測數(shù)據(jù)集為美國空軍實驗室公開的Gotcha數(shù)據(jù)集，由三通道X波段合成孔徑雷達系統(tǒng)采集，發(fā)射信號帶寬約為640 MHz，脈沖重復(fù)頻率為2 172 Hz，成像場景參考距離約為10 km，同時設(shè)置成像場景中包含一個合作的運動目標Durango，其運動速度和方向由車載全球定位系統(tǒng)同步記錄。數(shù)據(jù)整體長度約為71 s，如圖6(a)所示，為參考時刻t=46 s，相干積累時間為2 s的合成孔徑雷達成像結(jié)果，其中方框處為合作目標Durango和某一非合作目標。與仿真實驗類似，對Gotcha數(shù)據(jù)集要先進行距離徙動校正，以保證筆者所提算法的驗證的有效性。

圖6(b)為經(jīng)過多通道雜波抑制后的方框處成像結(jié)果，圖6(c)為基于呂氏分布時頻表示獲得的參數(shù)進行匹配濾波的成像結(jié)果。由圖6可見，目標得到了一定程度上的聚焦，但是效果仍然較差。圖6(d)和(e)分別為應(yīng)用1-范數(shù)正則化和參數(shù)化貝葉斯估計獲得稀疏恢復(fù)成像結(jié)果。通過對比可見，經(jīng)過稀疏恢復(fù)后的成像結(jié)果目標響應(yīng)旁瓣較低，且目標成像聚焦性能良好，其中基于筆者所提的參數(shù)化貝葉斯估計大動態(tài)成像算法獲得的成像響應(yīng)動態(tài)范圍較大，聚焦性能較好，背景雜波及噪聲抑制效果較好，相應(yīng)的圖像熵值亦可證明聚焦性能的提升。

圖6 成像結(jié)果

5 總 結(jié)

針對傳統(tǒng)方法對多個地面運動目標同時合成孔徑雷達成像時，目標相應(yīng)動態(tài)范圍較低的問題，筆者提出了一種基于參數(shù)化稀疏貝葉斯學習的合成孔徑雷達稀疏特征增強成像算法，并定量評估了二階多項式傅里葉字典A對重建性能和魯棒性的影響。仿真及實測Gotcha數(shù)據(jù)集均驗證了該方法的有效性，同時與傳統(tǒng)壓縮感知算法對比，顯示了筆者所提算法在性能上的優(yōu)越性和穩(wěn)健性。