偏場下薄膜體聲波諧振器頻率偏移的攝動分析

張大鵬　高楊　許夏茜

摘要：為準確預測測量力、熱場的薄膜體聲波諧振器（FBAR）傳感器的靈敏度，采用疊加于有限偏場之上的小增量場理論描述，提出一種攝動與有限元聯合求解方法。該方法利用COMSOL有限元軟件計算FBAR傳感器受外界載荷下其壓電層AlN的平均偏置應力，進一步在COMSOL中計算FBAR的諧振頻率與相應的振型，將有限元的計算數據代入攝動積分公式中，得到FBAR傳感器的頻率靈敏度。并以一個圓膜片FBAR為案例，介紹該方法用于計算圓膜片FBAR頻率-集中力靈敏度的詳細過程。采用攝動與有限元聯合求解方法得到的頻率靈敏度為41.3MHz/N，與文獻報道的實驗結果50MHz/N接近，驗證了方法的可行性。

關鍵詞：傳感器;薄膜體聲波諧振器;頻率偏移;攝動;有限元

中圖分類號：TP212.1;TB931

文獻標志碼：A

文章編號：1674–5124（2019）03–0012–06

Perturbation analysis of frequency shift in a thin film bulk acoustic wave resonator under biasing field

ZHANG Dapeng1， GAO Yang2， XU Xiaxi1

（1. School of Information Engineering， Southwest University of Science and Technology， Mianyang 621010， China; 2. Institute of Electronic Engineering， China Academy of Engineering Physics， Mianyang 621900， China）

Abstract： In order to accurately predict the sensitivity of thin film bulk acoustic wave resonator （FBAR） sensors for measuring mechanical or thermal field， a combined perturbation and finite element method is proposed based on the theory for small field superposed on the finite bias. Firstly， the average biasing stress of piezoelectric layer AlN of FBAR sensor under external load is calculated by COMSOL finite element software. Then， the resonant frequency and corresponding mode shape of FBAR are calculated in COMSOL. Finally， the calculated data of the finite element are substituted into the perturbation integral formula to obtain the frequency sensitivity of the FBAR sensor. The frequency sensitivity obtained by the perturbation and finite element method is 41.3 MHz/N， which is close to the reported experimental result of 50 MHz/N. The feasibility of this method is verified.

Keywords： sensor; thin film bulk acoustic wave resonator; frequency shift; perturbation; finite element

0 引言

1980年Lakin和Wang[1]公開了第一個薄膜體聲波諧振器（thin film bulk acoustic wave resonator，FBAR），FBAR便以其高Q值、小體積、可集成化等特點逐漸吸引了研究者的關注。隨著移動通信技術的發展，FBAR技術不僅在射頻濾波器應用中得到了飛速發展，在傳感檢測應用中也表現出了很大潛力[2]，比如生物化學檢測[3-4]、力學檢測[5-6]。FBAR換能器的生物化學檢測依賴于FBAR的質量負載效應，其靈敏度的預測方法由Sauerbrey方程[7]給出;力學檢測目前主要采用實驗測試[8-11]的方法，其靈敏度的預測方法報道較少，且存在有效性和易用性問題。文獻[12]提出了一種基于Mason模型的多尺度計算方法，文獻[13]提出了一種基于有限元的多尺度計算方法。這些方法都只修正了線性壓電理論中壓電材料的彈性常數，而偏場（力、電場）的存在會導致線性壓電理論失效，在偏場作用下壓電體的行為采用有效材料常數來描述，這是完全非線性壓電理論的結果。1971年Tiersten[14]給出了非線性壓電理論的基本方程組。對于諧振器在偏場作用下的行為，需要利用疊加于有限偏場之上的小增量場的線性方程來描述。Tiersten[15]在1978年給出了疊加于有限偏場之上的小增量場的線性方程的攝動公式，Sinha和Tiersten[16-17]利用該公式研究了溫度對諧振器的影響，Kosinski[18]利用攝動與結構理論相結合研究了石英晶體諧振器的加速度靈敏度，Masson等[19]利用攝動與Fahmy-Adler公式相結合研究了受準靜態應力的石英FBAR的應力靈敏度。文獻[14-19]均是研究的石英晶體諧振器，石英是單晶，而在以AlN（氮化鋁）為壓電材料的FBAR中，AlN實質是多晶，只是晶體在c軸（與c軸垂直的晶面為002面）方向有取向。因為體聲波是沿晶胞體內傳播，而沿c軸體聲波速率最快，大多數晶胞都是趨向于c軸垂直于基片，這樣體聲波才能較為順利的定向傳播，也即AlN薄膜呈多晶c軸擇優取向。利用上述方法預測AlNFBAR的頻率靈敏度并不能與文獻報道的實驗結果吻合。

針對以上不足，本文提出了一種攝動與有限元聯合求解的方法。利用有限元軟件計算FBAR壓電層在外界載荷下的平均應力、FBAR在無擾動下的諧振頻率和振動模態，再使用攝動積分公式得到FBAR傳感器的頻率靈敏度。通過圓膜片FBAR的案例，描述了方法的具體流程，并將計算結果與文獻[10]報道的實驗結果進行對比，驗證了方法的可行性。

1 模型建立與求解

1.1 攝動積分法

壓電晶體諧振器在偏場作用下，最終狀態可通過兩步到達：一是在初始偏場作用下產生有限靜態變形和電場;二是偏場之上的動態小增量場。這種情況可以通過求解一系列線性偏微分方程而得到諧振器的最終狀態，只不過方程的系數與初始變形和場有關，這就是疊加于有限偏場之上的小增量場的線性方程的攝動法。圖1所示為壓電晶體諧振器的3種構型。

1）參考構型。在t=0時刻，壓電體未發生形變而且不受電場作用。參考構型中的壓電體質點用X表示，其笛卡爾坐標為XK，壓電體的密度用ρ0表示。

2）初始構型。此時，壓電體上已受到有限靜電場或靜態力場作用，并且發生了有限靜態變形，這種變形和電場為偏場。此時壓電體質點X的位置為x=x（X），應變為E0，電勢為φ0（X），偏置位移w=x?X。

3）現時構型。向已在初始構型中發生靜態變形的壓電體之上再施加與時間相關的小增量變形與電場。X的最終位置由y=y（X，t）確定，最終電勢為φ0（X）+φ1（X，t），位移增量u（X，t）=y（X，t）?x（X），電勢增量為φ1（X，t）。

疊加在偏場之上的小增量場的線性壓電方程可以表示為：

其中，大寫指標表示參考構型;小寫指標表示現時構型;希臘指標表示初始構型;指標后面的逗號表示對坐標的偏微分，指標取值1，2，3，并服從愛因斯坦求和約定。第一Piola-Kirchhoff應力增量KL1γ和電位移增量?1K線性依賴于位移梯度和電勢梯度。GLγMα、RMLγ和LKL分別被稱為有效彈性常數、有效壓電常數和有效介電常數。不論是石英還是AlN，它們都是壓電耦合效應較弱的材料，因此可以只考慮有效彈性常數[17]：

其中，T-T0表示初始構型下壓電體受到的偏場，如壓力、溫度等;cLγMα和cLγMαKN分別被稱為二階和三階彈性勁度常數（除非特別指出，后文均簡稱為彈性常數）;c?LγMα被稱為彈性常數的偏置系數;?cLγMα為由偏場引起的彈性常數線性變化;δγα為Kronecker張量;wα，K表示偏置變形梯度;T1和E1分別表示由偏場導致的靜態偏置應力和應變。靜態偏置應力和應變定義為：

而均勻剛性介質的轉動在壓電振動的動力學中不起作用，應變矩陣對稱，因而可以得到：

將式（5）和式（6）代入式（3）中，可以得到

其中，sABLM為彈性順度常數（elastic compliance constant）;彈性順度矩陣[s]與彈性勁度矩陣[c]互為逆矩陣，即：

對于計算壓電諧振器受到環境因素（如在諧振器中引起偏場分布的溫度、力和加速度變化等）而導致的頻率漂移是以疊加于有限偏場之上的小增量場理論為基礎的特征問題。考慮純彈性非線性，Tiersten[15]給出了計算壓電諧振器由偏場引起的頻率漂移的一階攝動積分公式：

其中，ω和ωμ分別為擾動后和擾動前壓電諧振器的特征角頻率;?μ表示諧振角頻率的變化;式（11）給出的攝動積分公式看起來很復雜，但本質上可以理解為：H表示諧振器在振動模態下隨空間變化的有效彈性常數的加權平均值，其權重因子由振動模態的振型決定;gμγ表示對振動模態下實際位移uμγ的歸一化振型，壓電體的體積為V，上下標μ表示第μ個特征模態。一階攝動積分公式有效地將含偏場影響的復雜特征值問題式（1）分解為求解偏場的狀態問題和求解無偏場時的振動問題兩個相對簡單的問題。

對于測量力熱場的壓電傳感器而言，由偏場引起的頻率漂移還需要考慮彈性常數的線性變化?cLγMα，因此在式（11）中除了c?LγMα項，還要加上?cLγMα項，重寫式（11）為：

將式（14）代入式（10）中，通過變形可以得到由偏場引起的相對頻率偏移?μ為：

其中υL是壓電體表面S的法向量。假設表面應力為0，則式（15）右邊的面積分可以消去。將式（4）和式（7）代入式（15）中，得到：

若偏置應力T1在壓電體內分布是均勻的，KN可設材料輔因子k和振動模態因子U分別為：

因此諧振器頻率-偏置應力靈敏度ΓKN可寫為：

諧振器由偏場導致的相對頻率偏移可簡化為：

1.2 攝動與有限元的聯合求解

當FBAR傳感器受外界載荷時，FBAR受限于安裝結構而發生變形，此時引起FBAR的諧振頻率漂移最主要的機制是聲速的變化。在決定聲速的因素中，壓電層的彈性常數是最主要的因素。因此采用攝動與有限元聯合求解FBAR諧振頻率偏移的基本思路是：首先計算FBAR傳感器受外界載荷時，FBAR結構的偏置應力;然后計算FBAR壓電層的平均偏置應力，建立外界載荷與平均偏置應力的關系;接著利用有限元軟件求解FBAR的特征模態和特征頻率，并計算振動模態因子ULγMα;再利用攝動積分式（19）計算FBAR的頻率-應力靈敏度;最后根據外界載荷與平均偏置應力的關系，得到FBAR傳感器的頻率靈敏度。有限元軟件采用COMSOL Multiphysics軟件，具體步驟如下：

1）求解FBAR結構偏置應力。在COMSOL中建立FBAR傳感器的結構模型，加載外界載荷進行穩態求解，得到FBAR結構的偏置應力分布云圖。外界載荷可以是加速度、壓力或溫度。

2）計算FBAR壓電層的平均偏置應力。采用平均偏置應力可以簡化計算，并擬合出外界載荷與平均偏置應力的關系式。

3）求解FBAR的特征模態和特征頻率。建立單獨的FBAR結構模型，邊界條件與傳感器中保持一致，定義FBAR壓電層為積分域，使用特征頻率求解，得到FBAR縱波模式所對應的特征頻率和相應的振型，并計算振動模態因子ULγMα。

4）計算頻率-偏置應力靈敏度。利用壓電材料（AlN）彈性常數與應力的關系，得到dcLγMα的值，并計算材料輔因子kLγMαKN，將上述計算的數據代入式（19）中，可以得到FBAR的頻率-偏置應力靈敏度。5）計算FBAR傳感器的頻率靈敏度。利用擬合的外界載荷-平均偏置應力的關系式，得到FBAR頻率-外界載荷的靈敏度。

2 案例驗證

本算例的結構模型來自于文獻[10]中圓膜片型FBAR。在COMSOL軟件中建立圓膜片型FBAR結構的二維軸對稱模型，其疊層結構由下至上依次為支撐層Si（厚2μm）、絕緣層SiO2（厚0.4μm）、底電極Pt（厚0.15μm）、壓電層AlN（厚1μm）、頂電極Pt（厚0.15μm）、鈍化層Si3N4/SiO2（厚0.7μm/0.4μm）。設置其頂、底電極的電壓邊界條件分別為終端（1V）和接地（0V），側壁固定，對稱軸邊界條件為u（r）=0，即橫向位移為0，其二維軸對稱模型及邊界條件示意圖如圖2所示。外界載荷為集中力，作用于圓膜片FBAR的中心。計算過程中所涉及的材料參數如表1所示，AlN的三階彈性常數[20]如表2所示，表中與后面的計算均采用縮寫下標表示。AlN共有10個獨立的三階彈性常數，其他三階彈性常數均可通過對稱關系[21]求解得到。

利用COMSOL中穩態分析，圓膜片FBAR中心受到軸向的集中力載荷F，求解得到壓電層（AlN）的徑向平均（體平均）應力T1、T1和軸向平均12應力T31，并定義壓應力為正，拉應力為負。而軸向平均應力遠遠小于徑向平均應力，可以忽略。徑向平均應力與集中力載荷的關系如圖3所示，徑向平均應力（Pa）與集中力載荷（N）擬合關系式為：

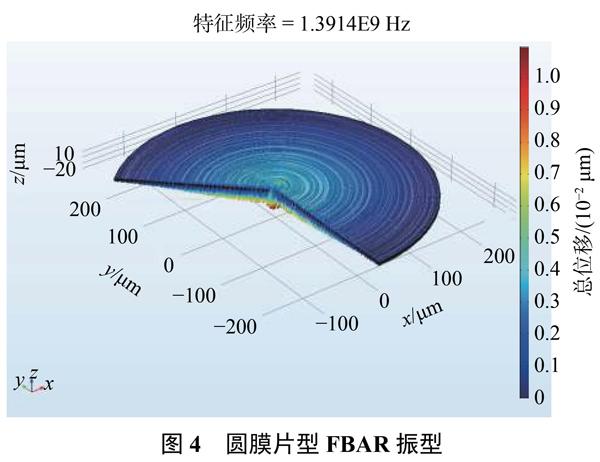
在FBAR傳感器中，FBAR僅僅是一個敏感元件，除了計算傳感器受外界載荷下壓電層的偏置應力，還要單獨建立FBAR的結構模型，用于計算FBAR的諧振頻率和相應的振型，并且邊界條件需符合傳感器結構。在此案例中，外界載荷直接作用于FBAR上，因此可以直接利用上述模型，不需要重新構建。利用COMSOL特征頻率分析求解FBAR的諧振頻率及其相對應的振型，得到FBAR的厚度拉伸模態（縱波模式）的振型如圖4所示，其諧振頻率約為1.3914GHz。定義FBAR壓電層為積分域，利用COMSOL的體積分計算振動模態因子。在FBAR中主要考慮的是縱波模式，因此只需要計算U33。得到U33=1.2625ppm/MPa。

利用AlN的二階彈性常數和式（8），計算得到彈性順度常數sABLM，利用表3中AlN應力-彈性常數的表達式[22]，計算得到dc33+dc33=?6.47，從表3中可以看出彈性常數對雙軸水平方向應力P//的一階導數約為彈性常數對單軸水平方向應力P/的一階導數的兩倍。將上述數據代入式（17）中，計算得到在縱波模式下受徑向應力時，材料輔因子k331+k332=?11.914。最后將數據代入式（19）并結合式（21）得到FBAR頻率-集中力載荷靈敏度約為41.3MHz/N，與文獻[10]的靈敏度50MHz/N接近。

3 結束語

本文提出了一種攝動與有限元聯合求解方法，利用COMSOL中的穩態分析求解壓電層AlN受到外界載荷下的平均偏置應力，建立外界載荷和平均偏置應力的關系，再利用COMSOL中的特征頻率分析求解FBAR的諧振頻率和相應的振型，最后利用攝動積分公式得到FBAR的頻率-外界載荷的靈敏度。使用攝動與有限元聯合求解方法計算了圓膜片FBAR案例的頻率靈敏度約為41.3MHz/N，與文獻報道的頻率靈敏度50MHz/N接近，驗證了方法的可行性。

參考文獻

[1] LAKIN K M， WANG J S. UHF composite bulk wave resonators[C]//Proc of IEEE Ultrasonics Symposium， 1980.

[2] GAO J N， LIU G R， LI J， et al. Recent developments of film bulk acoustic resonators[J]. Functional Materials Letters， 2016， 9（3）： 1630002.

[3]唐寧，常燁，劉晶，等.新型便攜式薄膜體聲波諧振氣體傳感器的研制與應用[J].納米技術與精密工程，2016（5）：331-336.

[4] PANG W， ZHAO H， KIM E S， et al. Piezoelectric microelectromechanical resonant sensors for chemical and biological detection[J]. Lab on a Chip， 2012， 12（1）： 29-44.

[5] CHIU K H， CHEN H R， HUANG R S. High-performance film bulk acoustic wave pressure and temperature sensors[J]. Japanese Journal of Applied Physics， 2007， 46（4A）： 1392- 1397.

[6] NAGARAJU M B， LINGLEY A R， SRIDHARAN S， et al. 27. 4 A 0. 8 mm 3±0. 68 psi single-chip wireless pressure sensor for TPMS applications[C]//Proc of IEEE International Solid- State Circuits Conference， 2015.

[7] ZHANG H， KIM E S. Micromachined acoustic resonant mass sensor[J]. Journal of Microelectromechanical Systems， 2005， 14（4）： 699-706.

[8] CAMPANELLA H， PLAZA J A， MONTSERRAT J， et al. Accelerometer Based on Thin-Film Bulk Acoustic Wave Resonators[C]// Proceedings of IEEE Ultrasonics Symposium， 2007.

[9] CAMPANELLA H， PLAZA J A， MONTSERRAT J， et al. High-frequency sensor technologies for inertial force detection based on thin-film bulk acoustic wave resonators （FBAR）[J]. Microelectronic Engineering， 2009， 86（4）： 1254-1257.

[10] CAMPANELLA H， CAMARGO C J， ESTEVE J， et al. Sensitivity of thin-film bulk acoustic resonators （FBAR） to localized mechanical forces[J]. Journal of Micromechanics and Microengineering， 2013， 23（6）： 065024.

[11] DELICADO A， CLEMENT M， OLIVARES J， et al. Influence of induced stress on AlN-solidly mounted resonators[C]//Proc of IEEE European Frequency & Time Forum，2016.

[12]高楊，趙坤麗，趙俊武.體聲波換能器靈敏度的微分-綜合分析法[J].強激光與粒子束，2016，28（6）：1-7.

[13]趙俊武.FBAR的應力負載效應研究[D].綿陽：西南科技大學，2017.

[14] TIERSTEN H F. On the nonlinear equations of thermo- electroelasticity[J]. International Journal of Engineering Science， 1971， 9（7）： 587-604.

[15] TIERSTEN H F. Perturbation theory for linear electroelastic equations for small fields superposed on a bias[J]. Journal of the Acoustical Society of America， 1978， 64（3）： 832-837.

[16] SINHA B K， TIERSTEN H F. First temperature derivatives of the fundamental elastic constants of quartz[J]. Journal of Applied Physics， 1979， 50（4）： 2732.

[17] SINHA B K， TIERSTEN H F. On the temperature dependence of the velocity of surface waves in quartz[J]. Journal of Applied Physics， 1980， 51（9）： 4659-4665.

[18] KOSINSKI J A. The fundamental nature of acceleration sensitivity[C]//Proc of IEEE International Frequency Control Symposium，1996.

[19] MASSON J， REINHARDT A， BALLANDRAS S. Simulation of stressed FBAR thanks to a perturbation method[C]//Proc of IEEE Mtt-s International Microwave Symposium Digest， 2005.

[20] PANDEY D K， SINGH D， YADAV R R. Ultrasonic wave propagation in IIIrd group nitrides[J]. Applied Acoustics， 2007， 68（7）： 766-777.

[21] BRUGGER， K. Pure modes for elastic waves in crystals[J]. Journal of Applied Physics， 1965， 36（3）： 759-0.

[22] WANG Z， ZHAO J， GAO Y， et al. First-principle studies on the influence of anisotropic pressure on the physical properties of aluminum nitride[J]. Materials Research Express， 2017， 4（1）： 016303.

（編輯：李剛）