噴水試驗機桁桿系統氣動優化設計

張鋒 宋銳紅

摘? ?要：基于理論估算，CFD分析和風洞試驗，在桁桿系統總體布局的基礎上，通過優化主桁桿剖面，確定小翼尺寸、安裝位置，解決了桁桿系統氣動優化設計中的主要參數選擇。獲得了滿足系統需求的總體氣動外形，通過飛行試驗對設計進行了檢驗。

關鍵詞：噴水試驗機? 桁桿剖面? 小翼? 計算流體力學

中圖分類號：V216.8? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1674-098X（2019）05（c）-0024-06

結冰飛行試驗是飛機定型試飛的高風險科目之一，傳統的結冰飛行試驗需要苛刻的氣象條件，ARJ-21飛機為了適航取證不得不遠赴北美進行自然結冰試驗，說明我們不具備可控的結冰飛行試驗條件。因此，研制不受氣象條件限制，可重復使用的結冰噴水試驗機，模擬結冰氣象微條件，對提升我國軍、民機防/除冰設計和定型試飛具有現實意義。

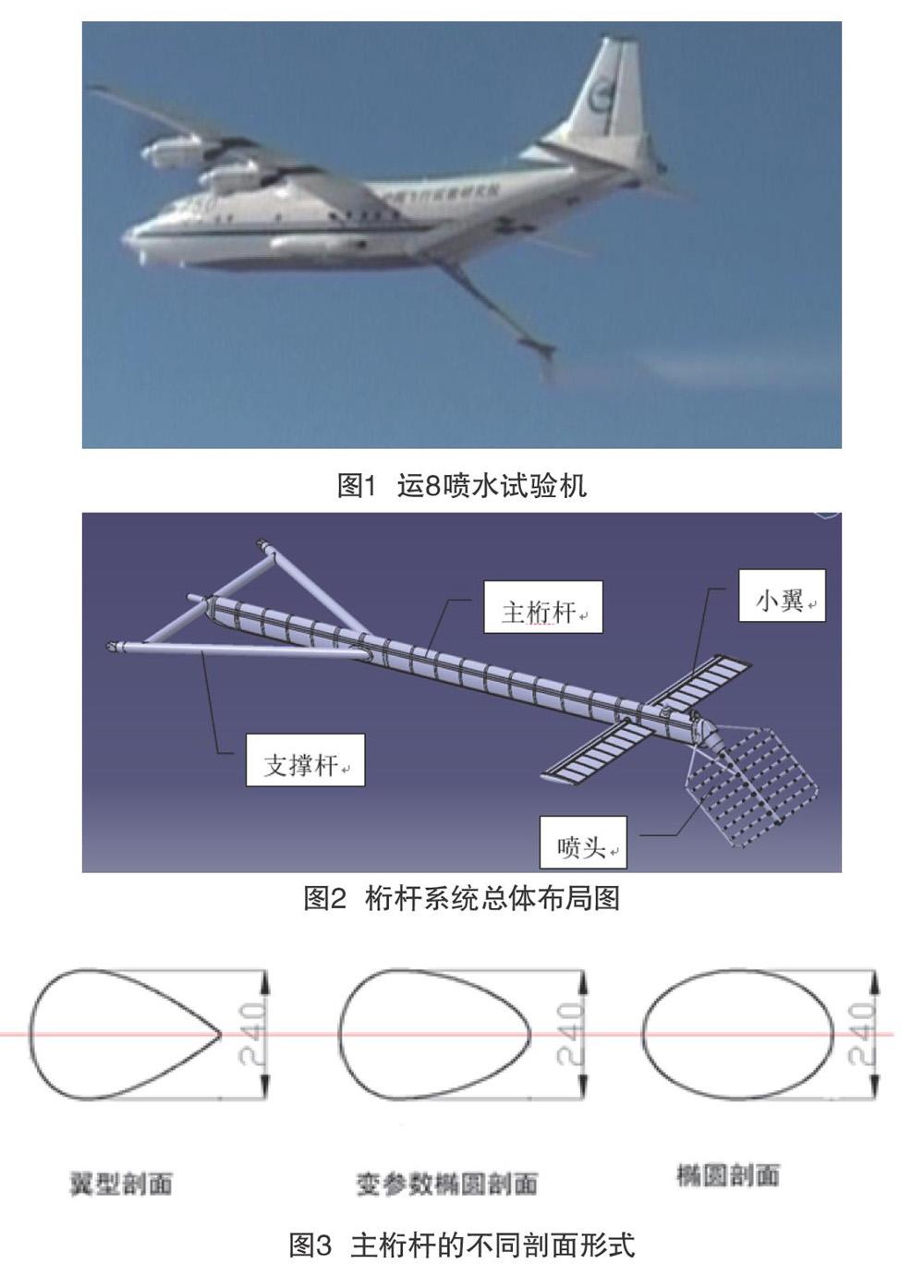
美國在20世紀50年代后期開始研究結冰噴水試驗機，距今已成功應用于多種軍、民型號飛機的結冰飛行試驗和冰風洞的驗證試驗[1]。本文研究的結冰噴水試驗機以運8飛機為載機平臺，在艙內加裝結冰試驗裝置，在機身外圍加裝桁桿系統，通過小翼操縱桁桿系統的縱向運動，待桁桿系統穩定在工作位置后，打開艙內的結冰試驗裝置，在桁桿系統的噴頭后方形成人工模擬結冰微環境，為被試飛機提供結冰試驗所需的氣象環境，加快型號研制周期，縮減試飛成本，見圖1[2]。

在試驗機的研制過程中，桁桿系統的氣動布局設計不僅關系到桁桿系統能否正常收放，是否滿足結冰噴水的試驗要求，同時對載機的飛行性能、飛行品質以及飛行安全有著較大的影響，成為改項目研制中的重點難點之一。

1? 桁桿系統總體布局設計

噴水試驗機桁桿系統為單自由度桁桿系統，主要由主桁桿、支撐桿、噴頭和小翼組成，總體布局如圖2所示。支撐桿為結構強度設計所附加，噴頭為成品件，主桁桿和小翼為本次優化設計的主要對象。經分析，主要設計目標、限制條件和設計參數如下。

1.1 設計目標

（1）桁桿系統對載機的氣動特性影響盡可能小;

（2）小翼有足夠的操縱效率實現桁桿系統的正常收放;

（3）桁桿系統下放角度30°～40°。

1.2 設計限制

（1）桁桿系統的尺寸、布局應與載機幾何協調;

（2）主桁桿剖面厚度不小于240mm，以保證內部管路、線路的空間需求。

1.3 設計參數

（1）主桁桿剖面形狀;

（2）小翼尺寸、安裝位置。

2? 主桁桿剖面優化設計

噴水試驗機主桁桿類似硬桿式加油機的加油桿[2]，具有典型的二元特性，其剖面形式的選擇不僅決定了整個桁桿的氣動特性，而且對載機的飛行性能及品質有著不可忽略的影響。

2.1 待選剖面

橢圓剖面由于具有二階光順、保凸性好、結構簡單等優點，是飛機整流外形常用的剖面形式，Kwon、Chitta、Benazza等對橢圓翼型升阻特性進行了數值計算研究[3-5]。翼型剖面也是氣動整流常用的剖面外形，當此剖面的長細比較小時會產生嚴重的氣流分離，甚至會出現升力線斜率反號的特殊現象[6]。變參數橢圓剖面位于橢圓剖面與翼型剖面之間，由于后緣較飽滿，可能具有相對較好的氣動特能。

分別選取翼型剖面，變參數橢圓剖面和橢圓剖面進行對比計算分析，其中翼型剖面采用NACA 0070翼型[7];橢圓剖面短軸/長軸比例為0.7;變參數橢圓剖面以30%為最大厚度點，前后分別使用Rho=0.414和0.35的二次曲線銜接而成，最大相對厚度保持70%。三種剖面厚度均為240mm，弦長約340mm，主桁桿長度8300mm，三種剖面形式見圖3。

通過CFD計算確定三種剖面桁桿的氣動特性。

計算狀態：高度H=4km，速度Vb=400km/h

計算構型：主桁桿處于工作位置。

2.2 計算結果

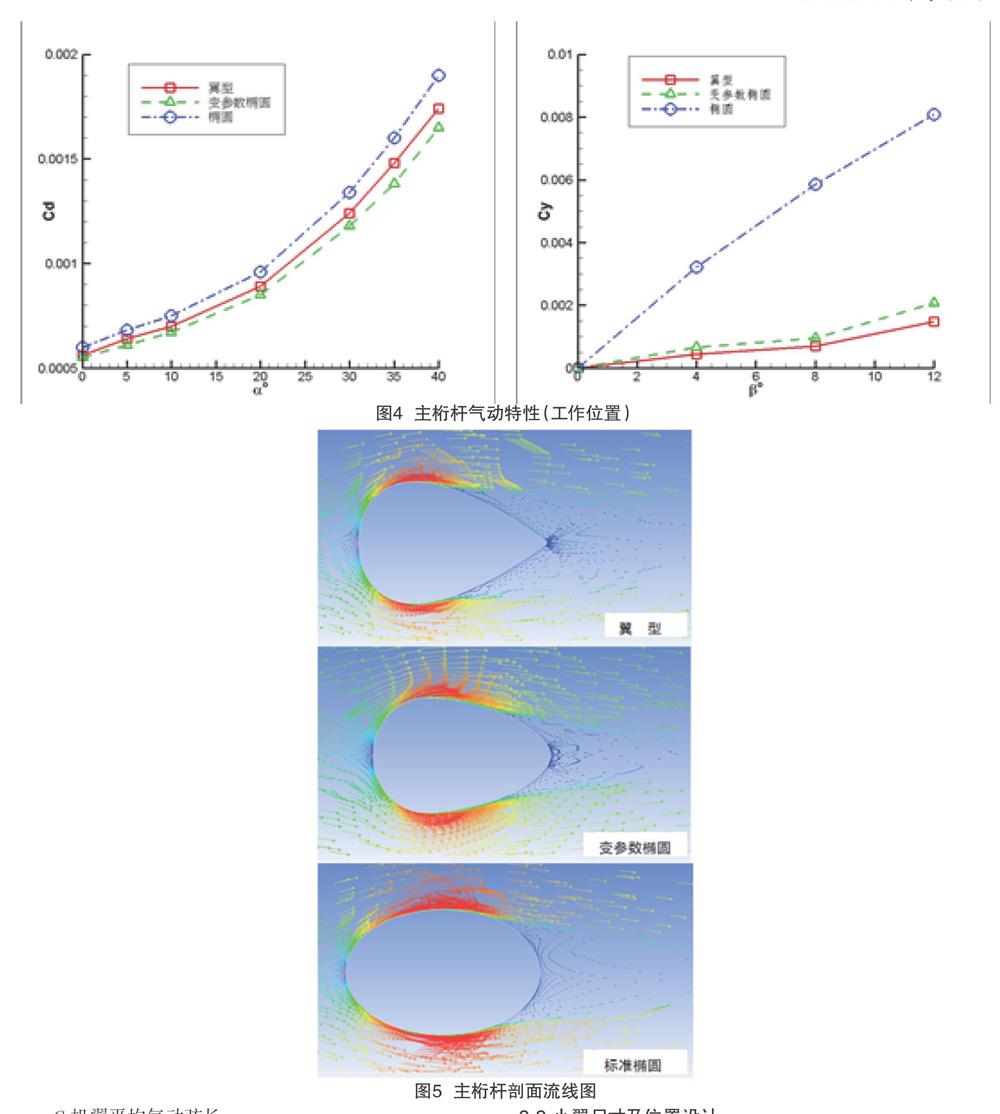
圖4為主桁桿處于工作位置時，三種剖面形式的側力/阻力特性。圖5為三種剖面形式的流線圖。

橢圓剖面桁桿的側力隨側滑角的增大明顯大于翼型和變參數橢圓剖面，這對單自由度噴水試驗機設計而言，對整個桁桿系統的結構設計非常不利;主桁桿在工作位置時，橢圓剖面桁桿的阻力最大，翼型剖面次之，變參數橢圓剖面桁桿的阻力最小;無側滑時翼型、變參數橢圓和橢圓剖面的氣流分離點分別在55%、75%和80%弦長，變參數橢圓剖面具有較小的氣流分離區，產生振動的風險相對較小。

在剖面弦長和厚度相同的基礎上，橢圓剖面、變參數橢圓剖面相對翼型剖面，其截面積和有效厚度有不同程度的增加，對于結構設計有利。

綜合以上分析，變參數橢圓剖面具有綜合較優的氣動和結構特性，可作為主桁桿剖面的優先選項。

3? 小翼尺寸及位置設計

小翼控制桁桿系統的收放運動，經分析，在桁桿系統的收放過程中，當桁桿系統處于工作位置時，在氣動力的作用下，桁桿系統產生一個較大的上升旋轉力矩，需要小翼產生足夠的負升力來平衡該上升力矩。這就要求小翼擁有足夠的舵效，來實現桁桿系統的正常收放。

3.1 小翼舵效研究

小翼舵效主要由其升力和安裝位置決定，小翼的升力通過桁桿作用在桁桿系統的轉軸處，產生旋轉力矩，以操縱桁桿系統的收放。同飛機俯仰力矩規定，小翼產生使飛機抬頭，桁桿系統下放的力矩為正。經分析研究，公式（1）為小翼相對桁桿系統轉軸的舵面效率，由于升力產生使桁桿系統上收的力矩，故公式（1）為負值。

（1）

其中：CLa小翼的升力線斜率;

ρ小翼處的密度（對于低速不可壓流動，）;

kq小翼區域速度阻滯系數;

小翼的面積;

L小翼25%氣動弦長距離桁桿系統轉軸的距離;

θ桁桿系統下放角度，θ=-18°～40°;

S機翼參考面積;

Ca機翼平均氣動弦長;

小翼為三維翼面，其流動特性不同于翼型剖面，存在展向流動，升力系數可通過公式（2）進行估算。

（2）

其中：小翼翼型的升力線斜率;

AR小翼展弦比，AR=4.5;

e效率因子，其典型值0.6～0.95之間，此處取0.8。

3.2 小翼尺寸及位置設計

經CFD計算，在低速情況下，無小翼的桁桿系統處于工作位置（約35°）時，其旋轉力矩系數大約為-0.015，若平衡該力矩所需小翼的偏角為10°，則小翼的設計舵效應為-0.0015。

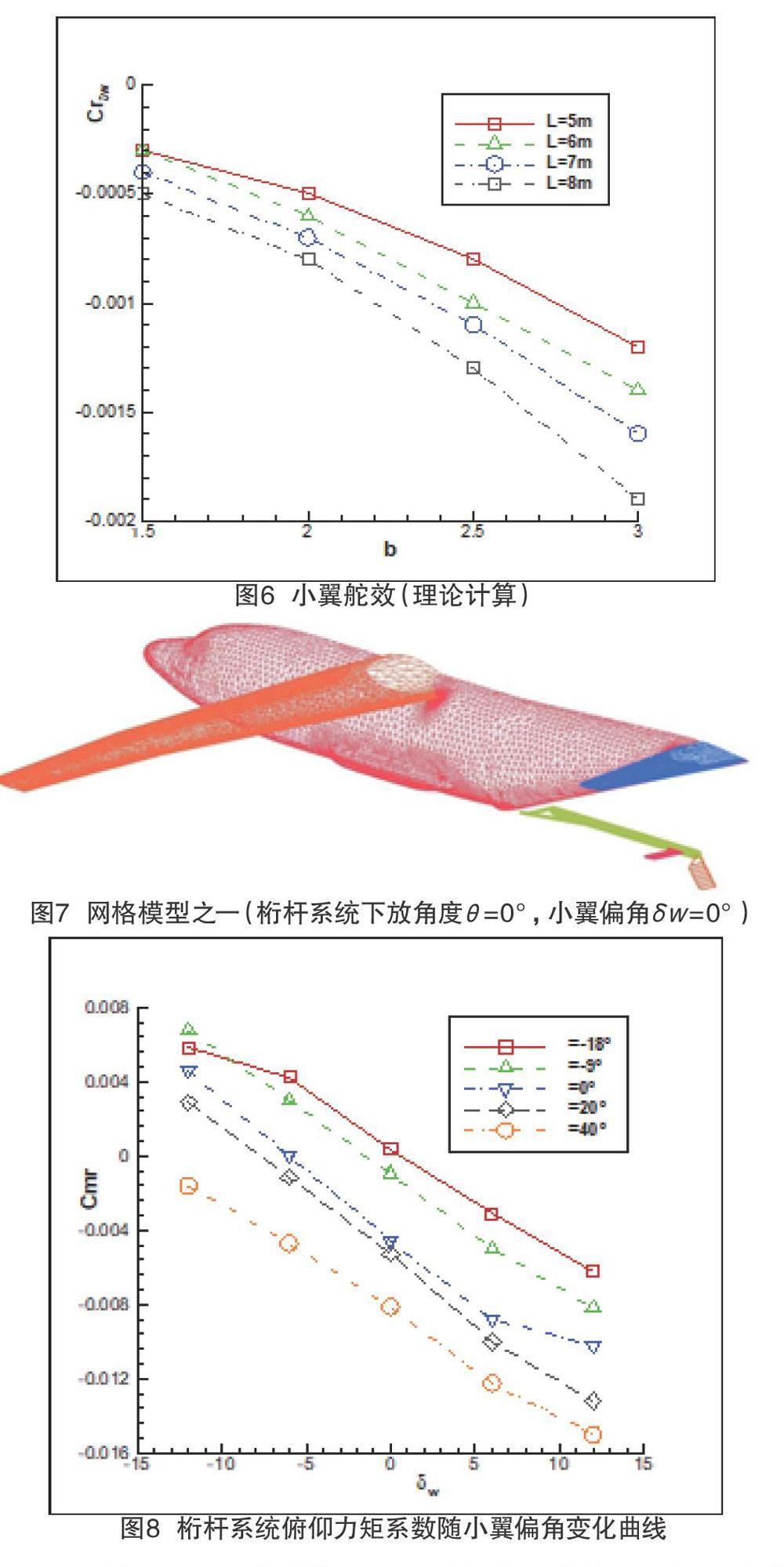
假設小翼采用經典的NA0012翼型，展弦比AR=4.5，展長b∈（1.5～3m），距離桁桿系統轉軸長度L∈（5～8m），根據公式（1），估算各種組合情況下小翼舵效如圖6所示。根據圖6的理論估算值，綜合考慮小翼舵效和桁桿系統結構設計的相容性，取展長b=2.8m，弦長c=0.6m，安裝位置L=7.25m，作為小翼尺寸及位置的初始設計值，此時小翼舵效約為-0.0015。

4? CFD計算分析

4.1 計算模型

為減小網格量，提高計算效率，計算模型采用半模形式，計算網格采用非結構網格，各網格模型均采用相同的參數設置，生成10層棱柱網格模擬飛機和桁桿系統的附面層，飛機第一層附面層網格高度為飛機平均氣動弦長的10-4量級，桁桿系統第一層附面層網格高度為小翼平均氣動弦長的10-4量級，相鄰兩層附面層厚度的比例為1.2，網格量大約為750萬。

桁桿系統模擬5個下放角度，分別為-18°，-9°，0°，20°，40°，在每個角度下，小翼角度分別設置為±12°，±6°，0°，共生成25套網格，圖7為桁桿系統下放角度θ=0°，小翼偏角δw=0°時的網格模型。

4.2 計算結果

圖8為飛行Ma=0.5，桁桿系統不同下沉角度時，其俯仰力矩系數隨小翼偏角的變化曲線。由計算結果可知：

（1）桁桿系統在不同角度下，其俯仰力矩系數隨小翼偏角的增加而較小，桁桿系統穩定性較好。

（2）桁桿系統在-18°～20°的范圍內，小翼有足夠的效率操縱桁桿系統。

（3）假設小翼的失速迎角為15°，通過外插延伸，可知該小翼可使桁桿系統最大下放到約-35°。

（4）當桁桿系統在收起狀態（θ=18°），小翼δw=-18°時，由于機身干擾，小翼上翼面處的流道變窄，小翼上翼面的壓力增量小于自由流中的理論增量，致使此時小翼的負升力增量小于自由流中的理論增量，這一負升力增量的減小降低了桁桿系統的旋轉力矩系數。

（5）當桁桿系統平行與機身水平線（θ=0°）時，由于機身干擾使小翼處的氣流產生較大的上洗，增加了此處小翼的實際迎角，當δw=12°時，小翼上翼面出現氣流分離，此時升力增量小于自由流中的理論升力增量，使得此時桁桿系統的旋轉力矩系數增量減小。圖9為此時小翼上翼面氣流的分離情況。

5? 風洞試驗驗證

5.1 試驗方法

為保證試驗數據的準確可信，模型采用反裝“增量法”安裝。反裝可避免風洞支架對桁桿系統的干擾，使飛機腹部及桁桿系統處在無干擾影響的氣流中。“增量法”可避免整體模型支架扣除的誤差、模型其它方面帶來的誤差及試驗數據全量的修正誤差。

流場觀察試驗采用“絲線法”。

試驗風速：測力試驗v≈70m/s，流場觀察試驗v≈40m/s。

試驗雷諾數：Re≈1.02×106。

模型支撐方式：前后兩點支撐。

5.2 主桁桿選型

圖11為主桁桿選型方案的阻力增量，試驗結果表明，桁桿系統下沉21°和42°時，變參數橢圓剖面桁桿相對翼型剖面桁桿減阻0.0007～0.0010，性能較優，與CFD計算分析趨勢一致。

5.3 桁桿收放角度試驗

（1）桁桿下沉30°，小翼偏角-15°，正常飛行迎角αw=4°～12°時，桁桿系統旋轉力矩系數CR>0，并留有適當的余量，可以實現下沉操縱;

（2）根據數據分析，小翼偏角-15°時，桁桿系統能夠下沉到36°，所以下沉限制偏角確定為36°。

6? 飛行試驗問題及解決辦法

（1）架次1：鎖止機構開鎖后，桁桿系統未正常下放。

原因分析：桁桿系統在收起狀態，小翼預設角度δw=0°（平行與桁桿系統），根據CFD計算分析，此時桁桿系統的氣動合力產生一個使其上收的力矩，在未操縱小翼的情況下，無法實現正常下放。

（2）架次2：桁桿系統正常收放，實現了噴水作業與最大下放角度驗證。

2015年12月28日，15：06：48秒，試驗機實現了持續約4min的噴水作業，此時桁桿下放角度θ=23°，小翼偏角δw=-13°。

2015年12月28日，15：14：45秒，桁桿系統實現了持續大約20s的最大下沉角度驗證，此時桁桿下放角度穩定在θ=32°，小翼偏角δw=-15°。

7? 結語

試驗機在氣動優化設計過程中準確把握了桁桿系統特殊布局的技術特點，通過理論分析、CFD計算和風洞試驗相結合的方式，解決了桁桿系統氣動優化設計的主要參數選擇。主要結論如下。

（1）變參數橢圓剖面具有綜合較優的氣動和結構特性，選定為主桁桿的剖面形式。

（2）通過理論分析小翼舵效、結合CFD計算，確定了小翼的尺寸及位置。

（3）通過CFD計算和風洞試驗，分析驗證了桁桿剖面的選型和桁桿系統的收放特性，為桁桿系統的飛行控制設計提供原始數據輸入。

（4）通過飛行試驗驗證了桁桿系統的設計，為進一步發展三自由度的噴水試驗機奠定了堅實的基礎。

參考文獻

[1] Russell A. Ashenden， Conducting Artificial Tailplane Icing Evaluations at the Air Force Flight Test Center， AIAA-95-0450 33rd Aerospace Sciences Meeting and Exhibit， January 9-12，1995/Reno， NV.

[2] Jeremy J.Simth*， Donald L.Kunz. Simulation of the dynamically coupled KC-135 Tanker and refueling boom. AIAA Modeling and Simulation Technologies Conference and Exhibit 20-23， August 2007.

[3] Kwon J， Choi S. Aerodynamic characteristics of elliptic airfoil at high Reynolds number[J]. Journal of Aircraft，2008，45（2）：641-650.

[4] Chitta V， Dhakal T P， Walters D K. Prediction of aerodynamic characteristics for elliptic airfoils in unmanned aerial vehicle applications， Low Reynolds number aerodynamics and transition， Genc MS（ED.）， 2012，InTech.

[5] Benazza A， Blance E， Abidat M. 2D Detached-eddy simulation around elliptic airfoil at high Reynolds number[J]. Journal of applied Science， 2011.

[6] Hoerner S F，Borst H V. Fluid-dynamic Lift 2ed[M].1985.

[7] C.H. Spenny. Boom Performance Envelope Expansion for Aerial Refueling With the KC-135 Tanker， AIAA/AHS/ASEE Aerospace Design Conference， February 16-19，1993.