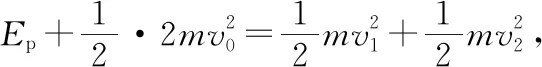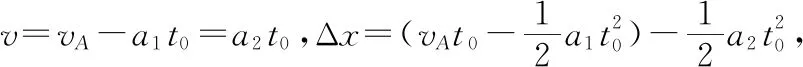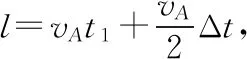高考動量守恒“高頻模型”分析與歸納
廣西
(作者單位:廣西區北海市合浦廉州中學)
動量守恒“高頻模型”命題特點分析與歸納
“高頻模型”為歷年高考試題中出現頻率比較高的模型,大多是高中物理主干知識。動量守恒定律是物理學中最基本的普適原理之一,也是高中物理教學的重要內容,同時還是高考考查的重點和熱點,在歷年高考中出現的頻率很高,尤其是幾種典型的“高頻模型”。這些模型多立足于現實生活的實際問題,考查學生物理核心素養及綜合分析能力。筆者通過研究歷年高考試題,總結幾種模型,并歸納解決此類題型一些方法,以饗讀者。
一、人船模型
人船模型是一種反沖現象,即由人和船兩個物體構成的系統,在該系統中,人和船在相互作用下各自運動,只有人與船的摩擦力,即摩擦力是內力,水面對船的阻力可以忽略不計,運動過程中該系統所受到的合外力為零,即人和船組成的系統在運動過程中總動量守恒。這類問題相互作用過程中系統的動能增大,有其他能向動能轉化。可以把這類問題統稱為反沖。
【例1】如圖1所示,質量為m的人站在質量為M長為L靜止小船的右端,小船的左端靠在岸邊。當他向左走到船的左端時,船左端離岸多遠?

圖1
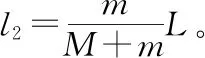
【點評】此結論與人在船上行走的速度大小無關,不論是勻速行走還是變速行走,甚至往返行走,只要人最終到達船的左端,那么結論都是相同的,人船模型問題是我們常遇到問題之一,本題所用方法和結果有普遍意義,但應注意l1、l2必須是相對同一參考系。
【擴展1】如圖2所示,一個傾角為α的直角斜面體靜置于光滑水平面上,斜面體質量為m,頂端高度為h,現有一質量為M的物體(M>m,且物體可以看做質點),沿光滑斜面下滑,當物體從斜面頂端自由下滑到底端時,斜面體在水平面上移動的距離是
( )
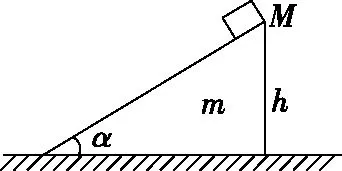
圖2
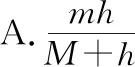
【分析】由于斜面體放在光滑地面上,則物體下滑的過程中,斜面后退,由平均動量守恒可列式求解,列式時要抓住兩物體運動的水平位移之和等于斜面的水平長度。
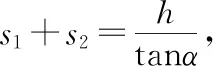
【點評】本題考查平均動量守恒定律的應用,要注意根據動量守恒得出兩物體質量與水平長度的乘積也是守恒的。
二、滑塊模型
滑塊模型是指物塊在木板上運動的情景,是一種物體相對運動的現象,由于兩物體之間有相互作用力,會出現相對滑動的物理情景。一般來說,滑塊受到木板的摩擦力約束,只能在一個平面上運動,無論相對靜止還是相對滑動,都要分析兩個物體之間的相互作用力。在高考中出現的題型各種各樣,主要以受力分析為突破口進行考查,涉及動量守恒、牛頓運動定律、能量守恒等內容。
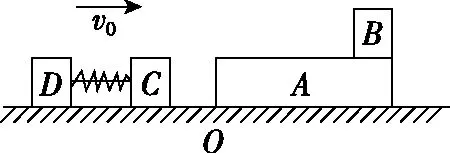
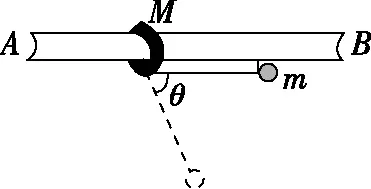
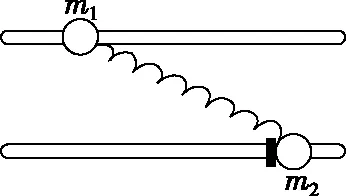
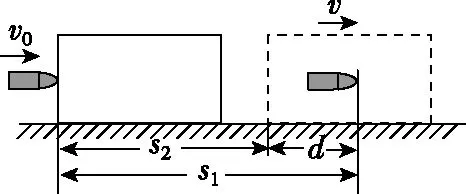
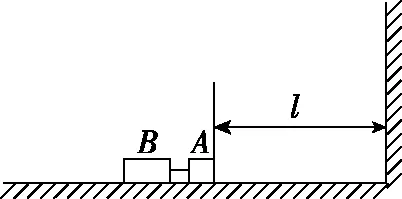
【例2】如圖3所示,一質量為M的平板車B放在光滑水平面上,在其右端放一質量為m的小木塊A,m 圖3 (1)A、B最后的速度大小和方向; (2)從地面上看,小木塊向左運動到離出發點最遠處時,平板車向右運動的位移大小。 【點評】本題關鍵是分析清楚兩物體的運動過程,此類問題內部滑動摩擦力做功發熱,能量守恒是我們常用方法Q=fs相對=Ek末-Ek初。 圖4 (1)滑塊C與A,B間的動摩擦因數及滑塊C滑行的時間; (2)若解除鎖定,再讓滑塊C以同樣的初速度滑上長木板A。則最終A、B的速度分別為多少? 【分析】A、B兩個長木板鎖定在光滑水平面上時,滑塊C從長木板A的左端進入剛好能停在長木板B的右端時速度為零,由功能關系求動摩擦因數μ,利用動量定理求運動時間。若解除鎖定,三個物體組成的系統動量守恒。最終C停在B上,且兩者速度相等,根據動量守恒定律和能量守恒定律結合求解。 【點評】本題綜合運用了動量守恒定律、動量定理和能量守恒定律,關鍵要正確選擇研究對象和研究過程,把握隱含的臨界情況和臨界條件,以及知道摩擦產生的熱量Q=fΔs=fL相對。 動量守恒定律是矢量式,研究的很多系統中,在某一方向上,系統符合動量守恒定律的條件,那么,在這一方向上則可以利用動量守恒定律列方程,計算復雜的運動過程。 【例3】如圖5所示,AB為一光滑水平橫桿,桿上套一質量為M的小圓環,環上系一長為L質量不計的細繩,繩的另一端拴一質量為m的小球,現將繩拉直,與AB平行,由靜止釋放該小球,則當細繩與AB成θ角時,圓環移動的距離是多少? 圖5 【點評】本題是以某一方向動量守恒為特點,以動量守恒定律等知識為依托,考查動量守恒條件的理解與靈活運用能力。 【擴展3】如圖6所示,水平光滑軌道寬和彈簧自然長度均為d,m2的左邊有一固定擋板,已知m1≥m2,m1由圖示位置靜止釋放,當m1與m2相距最近時m1速度為v1,則求在以后的運動過程中( ) 圖6 A.m1的最小速度是0 C.m2的最大速度是v1 爆炸類的模型,主要考查的是研究系統某一瞬間出現爆炸的情景。在爆炸的過程中,內力遠大于外力,則系統可以近似處理為動量守恒。爆炸模型類似反沖特點,這類問題相互作用過程中系統的動能增大,有其他能向動能轉化。 【例4】拋出的手雷在最高點時水平速度為10 m/s,這時突然炸成兩塊,其中大塊質量300 g仍按原方向飛行,其速度測得為50 m/s,另一小塊質量為200 g,求它的速度的大小和方向。 【分析】手雷在空中爆炸時所受合外力應是它受到的重力G=(m1+m2)g,可見系統的動量并不守恒。但在爆炸瞬間,內力遠大于外力時,外力可以不計,系統的動量近似守恒。 【點評】爆炸類的題型類似于反沖,都是由其他形式的能轉化為動能。 子彈打木塊實際上是一種完全非彈性碰撞。作為一個典型模型,它的特點是子彈以水平速度射向原來靜止的木塊,并留在木塊中與木塊共同運動,下面從動量、能量和牛頓運動定律等多個角度來分析這一過程。 【例5】設質量為m的子彈以初速度v0射向靜止在光滑水平面上的質量為M的木塊,并留在木塊中不再射出,子彈鉆入木塊深度為d。求木塊對子彈平均阻力的大小和該過程中木塊前進的距離。 圖7 【點評】這個式子的物理意義為f·d恰好等于系統動能的損失;根據能量守恒定律,系統動能的損失應該等于系統內能的增加;可見f·d=Q,即兩物體由于相對運動而摩擦產生的熱(機械能轉化為內能)等于摩擦力大小與兩物體相對滑動的路程的乘積(由于摩擦力是耗散力,摩擦生熱與路徑有關,所以這里應該用路程,而不是用位移)。做這類題目時一定要畫好示意圖,把各種數量關系和速度符號標在圖上,以免列方程時代錯數據。 圖8 【點評】對于復雜的物理問題要搞清物理過程,要明確是否滿足動量或機械能的守恒條件,特別是碰后的兩物體有共同速度的情況,機械能損失最大,所以動量守恒時,機械能不一定守恒。 【例6】甲乙兩球在水平光滑軌道上同方向運動,已知它們的動量分別為P甲=5 kg·m/s,P乙=7 kg·m/s,甲從后面追上乙并發生碰撞,碰撞后乙球動量變為10 kg·m/s,則兩球質量m甲與m乙間關系為 ( ) A.m甲=m乙B.2m甲=m乙 C.4m甲=m乙D.6m甲=m乙 【點評】碰撞的特點為①作用時間極短,內力遠大于外力,總動量總是守恒的;②碰撞過程中,總動能不增加,因為沒有其他形式的能量轉化為動能;③碰撞過程,兩物體產生的位移可忽略。 【擴展3】靜止在水平地面上的兩小物塊A、B,質量分別為mA=1.0 kg,mB=4.0 kg;兩者之間有一被壓縮的微型彈簧,A與其右側的豎直墻壁距離l=1.0 m,如圖9所示。某時刻,將壓縮的微型彈簧釋放,使A、B瞬間分離,兩物塊獲得的動能之和為Ek=10.0 J。釋放后,A沿著與墻壁垂直的方向向右運動。A、B與地面之間的動摩擦因數均為μ=0.20,重力加速度取g=10 m/s2。A、B運動過程中所涉及的碰撞均為彈性碰撞且碰撞時間極短。 圖9 (1)求彈簧釋放后瞬間A、B速度的大小; (2)物塊A、B中的哪一個先停止?該物塊剛停止時A與B之間的距離是多少? (3)A和B都停止后,A與B之間的距離是多少? 對于高考壓軸題來說,運動的多重性、研究對象的復雜性是解決問題的關鍵。三體兩次作用的問題,主要是多過程交織在一起,試題具有一定的難度。 【例7】如圖10所示,長木板A靜止放在水平地面上,其右端疊放著物塊B,左端恰好在O點,水平地面以O點為界,左側光滑,右側粗糙。物塊C(可以看作質點)和物塊D之間夾著一根被壓縮的彈簧,并用細線鎖住,此時彈簧的彈性勢能為8 J,兩者以共同的速度v0=6 m/s向右運動,某時刻細線突然斷開,物塊C與彈簧分離后,撤去物塊D,物塊C與長木板A碰撞并與之粘連(碰撞時間極短)。已知A、B、C、D的質量均為m=2 kg,木板A的長度l=6 m,A、C與粗糙地面間的動摩擦因數相同,均為μ1=0.1,A、B間的動摩擦因數為μ2=0.2,最大靜摩擦力等于滑動摩擦力,重力加速度為g=10 m/s2。 圖10 (1)求物塊C和彈簧分離時物塊D的速度大小; (2)求最終物塊B離長木板A左端的距離; (3)若物塊C與長木板A碰撞的同時,在長木板A的右端施加一水平向右的恒力為F=18 N,經過一段時間后撤去,物塊B剛好不從長木板的左端滑出,求恒力F作用的時間。 圖11 【點評】本題的問題比較復雜,過程也比較多,對于復雜的物理問題要搞清物理過程,要明確是否滿足動量或機械能的守恒條件,特別是碰后的兩物體有共同速度的情況,機械能損失最大,所以動量守恒時,機械能不一定守恒,這時應注意用動能定理或者功能關系進行求解。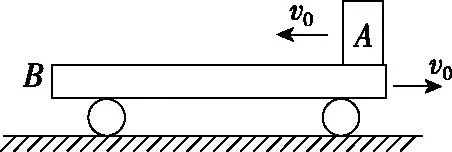
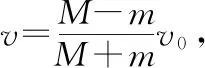
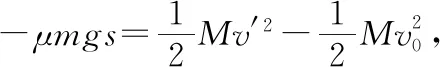
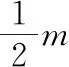

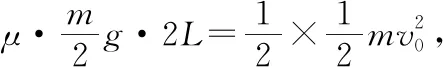
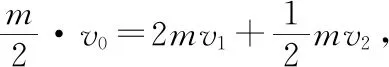
三、某一方向上的動量守恒
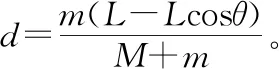
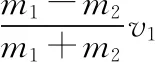
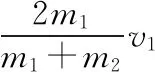
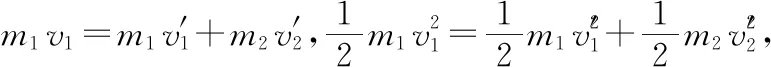
四、爆炸類問題
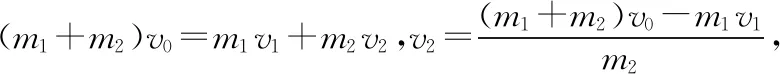
五、子彈打木塊模型
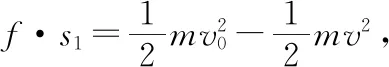
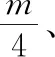
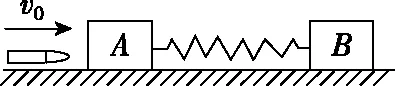
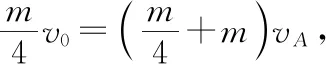
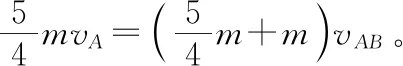
六、碰撞模型
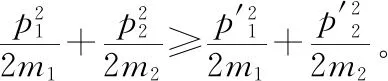
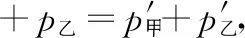
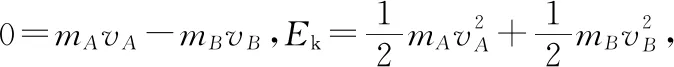
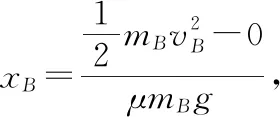
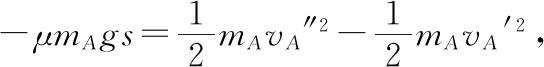
七、三體兩次作用模型(能量和動量綜合問題)