水平井多級分段模型算法及射孔簇設計
(中國石油集團測井有限公司新疆分公司,新疆 克拉瑪依 834000) (荊州三方石油技術開發有限公司,湖北 荊州 434000) (中國石油集團測井有限公司新疆分公司,新疆 克拉瑪依 834000) (長江大學計算機科學學院,湖北 荊州 434023)
為解決致密儲層物性差、孔喉細小、非均質性嚴重、裂縫發育等問題,很多油田都是通過壓裂進行人工造縫,采用分段多簇壓裂方式,改善儲層流體的滲流條件[1,2]。因此,水平井的射孔簇設計在生產實際中起著非常重要的作用。很多研究者對壓裂效果進行了一些頗有成效的研究[3~5],但在生產實際中,面對的主要問題是如何在一個水平井中設計相應的射孔簇位置,以期達到壓裂效果好和費用少的目的。為了控制成本,往往會事先確定一個對應井段的射孔簇數,而為了提高壓裂效率,則是希望利用測井數據等資料選取射孔簇的位置。目前,文獻[6]提出了一種逐步選點的方法,中國石油集團測井有限公司新疆分公司利用人工,根據曲線的一致性和射孔簇數將井段分成若干段,然后再在段內選取較好壓裂點,其工作繁瑣,花費大量工時而且要求設計人員具有較為扎實的專業技術知識。為了提高效率和可行度,需要利用相應的測井資料進行自動化分段和射孔簇設計。
1 水平井多級分段模型
水平井的水平井段長度一般在1000~2000m。對致密砂礫巖油藏,一類儲層50m左右一段壓裂效果最好,二類儲層60m左右一段壓裂效果最好;對頁巖油油藏,一類儲層40m左右一段壓裂效果最好,二儲層50m左右一段壓裂效果最好。
水平井的水平井段一般都有自然伽馬、密度、聲波時差、聲波幅度等曲線,采集常規9條測井曲線,分別反映儲層的巖性、物性、電性、機械特性,需要利用測井曲線來反映儲層的特性,分段時需要考慮敏感因素,不同的敏感因素的作用大小不同。
不同沉積環境導致了物源、水動力條件等的不同,從而造成沉積物組合形成和層序特征的不同,反映到測井曲線上就是不同的曲線形態。目前,測井曲線的形態大致被分為箱形、鐘形、漏斗形和復合形4類[7]。而在人工進行多級分段射孔簇的設計中,就是依據測井曲線的分類,把相似的曲線盡量分在同一段,然后在同一段中則依據相應的測井取線,如脆性指數等,設計射孔簇的位置。
顯然,上述需要人工依據曲線形態進行分段的方法效率極為低下,并且不可避免的產生人為誤差。如果能夠將相似性比較自動化,就會極大提高工作效率,并能避免人為誤差。
進一步分析發現,問題的實質就是對有序樣品的分類。實際生產中面對的問題就是:對于給定的數據曲線{xn},n= 1,2,3,…,N,需要將其分成k段,并要求每段內的曲線形態保持一致。由于曲線形態的定義很難參數化,需要尋求一個相對一致的判斷標準對該問題進行自動化。目前一個比較有效的判斷標準就是段內離差,也是最優分割[8]的一個判斷標準。于是問題就變成:對于給定的數據曲線{xn},n= 1,2,3,…,N,需要將之分成k段,并要求每段的段內離差最小。同時,為了完成射孔簇的設計,必須保證每段長短的相對平衡,所以在分段時會對每段的長度有限制,也就是每段的長度有一個最大值和最小值。由此可以得到如下數學模型:
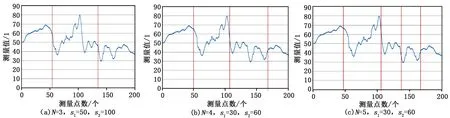
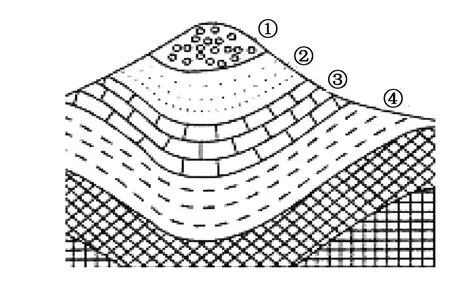
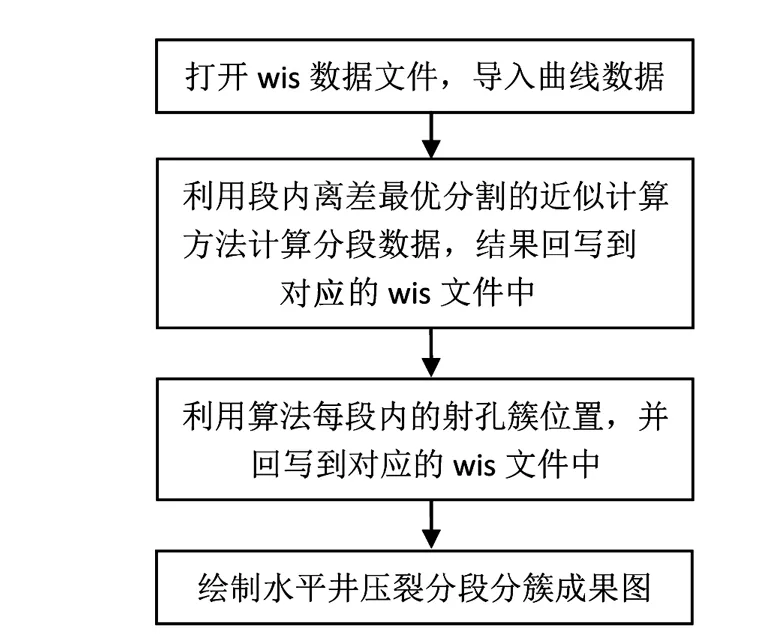
對于給定的有序信號{xi},i=1,2,…,n,正整數k,s1,s2,求1=a1 1)s1≤a-ai-1≤s2,2≤i≤k+1; 有序樣品的分割越來越受到重視,各種算法得到了廣泛的研究[9,10],但是生產實踐的應用和推廣則需要穩定正確的算法,最優分割算法就是一個較為理想的算法。最優分割是基于離差分析的對有序樣品進行分割的一種統計方法。設有n個按一定順序排列的樣品,為討論簡便,假設每個樣品觀測了一項指標,原始資料為x1,x2,…,xn,現要在不破壞原有順序條件下將n個樣品分成若干段,比如要分成L段。最優分割算法的基本原理就是它使得各段內部樣品之間的差異性最小,而各段之間的差異性最大,在地質分層等領域得到廣泛應用[1,11]。其算法基本過程如下: 對{x1,x2,…,xn}確定最優L分割,可先找出前j個數的最優L-1分割的最優段內離差: Wj(L-1;α1(j),α2(j),…,αL-2(j)) (j=n-1,n-2,…,L-1) (1) 式中:αi(j)(j=1,2,…,L-2)表示前j個數的第i個分割點。 {x1,…,xα1(j)},{xα1(j)+1,…,xα2(j)},…,{xαL-2(j)+1,…,xj}與{xj+1,xj+2,…,xn}構成一個L分割,但不一定是最優的L分割,可選擇一個使WN(L;α1(j),α2(j),…,αL-2(j),j)=Wj(L-1;α1(j),…,αL-2(j))+dj+1,n為最小的j,即得最優L分割。設j=αL-1時WN(L;α1(j),…,αL-2(j),j) 最小,即: 可得最優L分割: {x1,…,xα1}{xα1+1,…,xα2}…{xαL-1+1,…,xn} 這個算法顯然需要遞歸進行,其時間復雜度是指數增長的,所以當樣品個數多,分段數也較多的情況下難以進行有效的計算。 對于給定的有序樣品序列{x1,x2,…,xn},為了將其分割成k段,只需選取k-1個端點,1≤a1 基于組合生成算法的最優分割算法步驟如下: Step 1 輸入分割段數k,樣品數據{xi},i=1,2,…n; Step 2 求取離差矩陣D=(dij)n×n,dii=0,而當i與j不同時: Step 3y1=a1=1,y2=a2=2,…,yk-1=ak-1=k-1。W=dkn; Step 4S={j|aj Step 5 如果S為空集,輸出y1,y2,…,yk-1,算法終止,否則轉Step 6; Step 6 設i為S中的最大整數,作如下操作: 1)ai=ai+1; 2)aj=aj-1+1,j=i+1,i+1,…,k-1; 3)W1=d1,a1+da1+1,a2+…+dak-1,n; Step 7 如果W1 為了滿足約束條件,需要適當修改此算法中的分割點的取值,保證其滿足對應的約束,就可以得到求解水平井多級分段模型的算法。 基于段內離差的帶約束的分段算法步驟如下: Step 1 Set={},W=MAX_FLOAT,給定有序信號{xi},i=1,2,…n; Step 2 計算段直徑矩陣D=(dij)n×n,其中,dii=0,而i≠j時: Step 3a1=1,a2=a1+s1,…,aN=aN-1+s1; Step 4 如果ai-ai-1 Step 5W1=d1,a1+da1+1,a1+…+daN,n,如果W1 Stpe 6S={j|aj Step 7 如果S為空集,輸出Set,算法終止; Step 8 設i為S中的最大整數,作如下操作: 1)ai=ai+1; 2)aj=aj-1+s1,j=i+1,i+2,…,N; Step 9 回到Step 4。 基于段內離差的帶約束的分段算法可以求得水平井多級分段模型的精確解(見圖1),在分段數遠小于樣品數(k?n)時是個P類算法,其時間復雜度大約為O(nk)。但是在分段數較多時其時間復雜度則是指數函數,為了降低時間復雜度,可以利用二分法進行分割,其效率和實用性也得到了廣泛的關注和應用[12],但在地層的分割中效果不盡人意。 圖1 基于段內離差的約束分段算法試驗結果 圖2 地層剖面圖 如果考慮的是地層劃分,如圖2某區塊有4個地層組成,那么②、④兩層可能比較相似,但是①、②層和②、③層區分度卻可能比較大,就不必進行總體劃分,只需要找到當前兩層的劃分點即可,反映到數學上就是只需要確定當前兩層的段內離差較小就行,利用該原則可以設計了一個段內離差最優分割的近似計算方法。 段內離差最優分割的近似計算方法步驟如下: Step 1 Set={a1=1,a2,…,ak,ak+1=n},給定有序信號{xi},i=1,2,…n,m=1; Step 2 計算段直徑矩陣D=(dij)n×n,其中,dii=0,而i≠j時: Step 3 如果m=k,輸出Set,終止; Step 4t=am+1=am+s1; Step 5W=MAX_FLOAT; Step 6 如果n-t<=s1×(k-m),轉到Step 8; Step 7 計算由t還分的第m段的離差與可能的第m+1段的離差的和W1,如果W1 Stpe 8m=m+1,返回到Step 4。 圖3 水平井多級分段、射孔簇設計流程 此算法Step1、2時間復雜度是O(1),Step4~8是O(k),Step6、7是O((s2-s1)2),所以其算法的時間復雜度是O(k(s2-s1)2)。 應用筆者設計的算法就可以得到一個高效的射孔簇設計方法,其主要原理如下:通過選取的測井數據,對需要設計射孔簇的井段進行分段,然后選取適當的測井數據,如脆性指數等,根據實際需求,包括每段的射孔簇數,射孔簇的距離以及結箍位置等,進而計算每段中的射孔簇的位置。其流程圖如圖3所示, 分段數據表和射孔簇位置表樣例如圖4所示,射孔簇設計圖如圖5所示。 圖4 分段數據表和射孔簇位置表樣例 圖5 xxx21井射孔簇設計圖 1)提出了帶約束的有序樣品基于段內離差的分割數學模型,并為此問題設計了相應的求解算法。 2)通過底層數據的特點的分析,提出并設計了帶約束的有序樣品基于段內離差的分割問題的近似計算方法,進而為生產實踐的應用提供了一個行之有效的工具。 3)在實際生產中充分利用現有技術以及成熟的段內離差最優分割算法,設計并完成了一套水平井射孔簇設計應用軟件,實現了水平井射孔簇設計的自動化,極大提高了工作效益。實踐應用證明,段內離差最優分割算法計算結果合理、準確,滿足水平井射孔簇設計要求。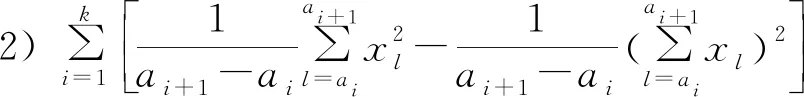
2 水平井多級分段模型的算法設計
3 基于多級分段模型的射孔簇設計

4 結論

