大鱗鲃形態性狀與體質量的相關性及通徑分析

(江蘇省漁業技術推廣中心， 江蘇 南京 210036) (江蘇省揚中市水產技術推廣站，江蘇 揚中 212200) (江蘇省揚中市新壩鎮農業服務中心，江蘇 揚中 212211)

大鱗鲃(Barbuscapito)隸屬于鯉形目(Cypriniformes)、鯉科(Cyprinidae)、鲃亞科(Barbinae)、鲃屬(Barbus)，又名淡水銀鱈魚、淡水鱈魚，主要分布于里海南部和咸海水系、烏茲別克斯坦、伊朗和土耳其等地的內陸河流，原產地是烏茲別克斯坦的阿姆河，是當地重要的大型經濟魚類[1]。2003年，中國水產科學研究院黑龍江水產研究所將大鱗鲃野生個體引種到我國，此后在山東、黑龍江、天津、江蘇等地區都進行了大鱗鲃咸、淡水養殖的嘗試，豐富了我國北方鲃魚的養殖品種。近年來，大鱗鲃在各地區的人工繁殖和池塘養殖技術有了突破性進展，與我國本土鲃魚種類相比，大鱗鲃食性廣、肉質鮮美、生長迅速、耐鹽堿能力強，已成為我國具有較高價值和較好市場前景的經濟魚類[2～9]。通過對大鱗鲃養殖群體進行系統的良種選育，可有效緩解近親繁殖帶來的種質資源及生物學性狀退化的問題，其外部形態特征成為最直觀、最便于測量的目標性狀[10, 11]。通徑分析是一種用于研究變量之間因果關系的統計方法，被廣泛應用于水產養殖的方案優化和產量估計等方面，目前，通徑分析及多元回歸分析已在真鯛(Pagrosomusmajor)[12]、大西洋鮭(Salmosalar)[13]、河川沙塘鱧(Odontobutispotamophila)[14]等魚類以及蝦、蟹、貝類[15～20]研究中使用。

下面，筆者選用1齡大鱗鲃，測量其體質量和各形態性狀后進行多元分析，通過相關分析、通徑分析和回歸分析，確定了影響大鱗鲃體質量的主要形態性狀及其直接和間接影響效果，建立了估計體質量的最優回歸方程，可為大鱗鲃的選育工作提供參考依據。

1 材料與方法

1.1 試驗材料

2018年6月5日從江蘇省漁業技術推廣中心揚中基地隨機選取1齡大鱗鲃280尾，其體質量1.14～5.94g，體長40.60～77.89cm。

1.2 測量方法

數據的測量參照伍獻文等[21]和王鴻媛[22]的方法，測定體質量(Y)、體長(X1)、體高(X2)、頭長(X3)、體寬(X4)、尾柄高(X5)、尾柄長(X6)、吻長(X7)、眼徑(X8)、眼間距(X9)等10個性狀。各形態性狀的測量使用游標卡尺，精確到0.01cm。體質量測量用電子天平，精確到0.01g。

1.3 數據分析與計算

使用SPSS 19.0統計軟件和Excel 2011對試驗數據進行分析，獲得各性狀表型參數包括平均數、標準差和變異系數等，利用SPSS 19.0統計軟件中的K-S單樣本檢驗(Kolomogorov-Simirnov one sample test)各性狀的分布是否符合正態分布。參照杜家菊等[23]的方法對各性狀表型數據進行Pearson相關分析和形態性狀指標對體質量的通徑分析。根據通徑分析基本原理，將相關系數剖分為各形態性狀對體質量的直接作用(通徑系數)和間接作用。依據相關分析和通徑系數計算決定系數，決定系數包括單個性狀對體質量的決定系數和兩個性狀對體質量的共同決定系數。運用逐步多元線性回歸法，通過偏回歸系數檢驗剔除不顯著的性狀，取偏回歸系數顯著的形態性狀對體質量建立多元回歸方程，并對方程進行擬合度檢驗。相關計算方法參照文獻[24, 25] 的方法，數據間的比較以P<0.05時為差異顯著，P<0.01時為差異極顯著。

2 結果與分析

2.1 各性狀的表型參數

所測280個大鱗鲃的表型數據資料經初步整理后的結果見表1。單個性狀進行K-S正態分布檢驗，P值均大于0.05，說明每個性狀的數據服從正態分布，可以對這些性狀進行進一步的通徑分析。在這些性狀中，以體質量的變異最大，體長的變異最小。變異系數是選擇潛力的一個指征，可作為衡量群居魚大小變動即生長離散程度的尺度。由表1可知，體質量的變異系數最大，說明其具有較大的選擇潛力，然后依次是體寬、吻長和體高；而體長和頭長的變異系數較小，選擇潛力較弱。

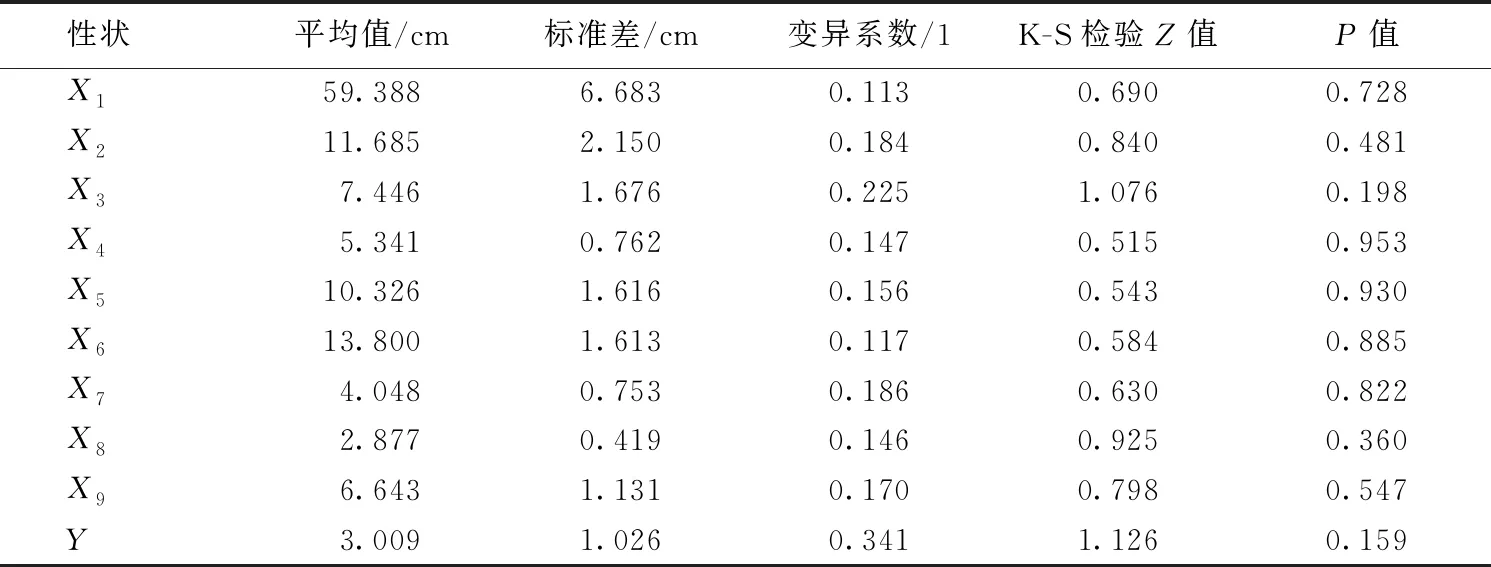
表1 各性狀表型參數(n=280)

注：體質量單位為g。

2.2 性狀間表型相關系數

對大鱗鲃各性狀進行表型相關分析，獲得各性狀間的表型相關系數(見表2)。結果顯示，兩兩性狀之間均極顯著(P< 0.01)正相關。體長、體高、頭長等各形態性狀與體質量間的相關系數大小依次為：體長(X1)>頭長(X6)>體高(X2)>尾柄高(X4)>體寬(X3)>眼間距(X9)>尾柄長(X5)>吻長(X7)>眼徑(X8)，表明所選指標進行相關分析具有重要的實際意義。

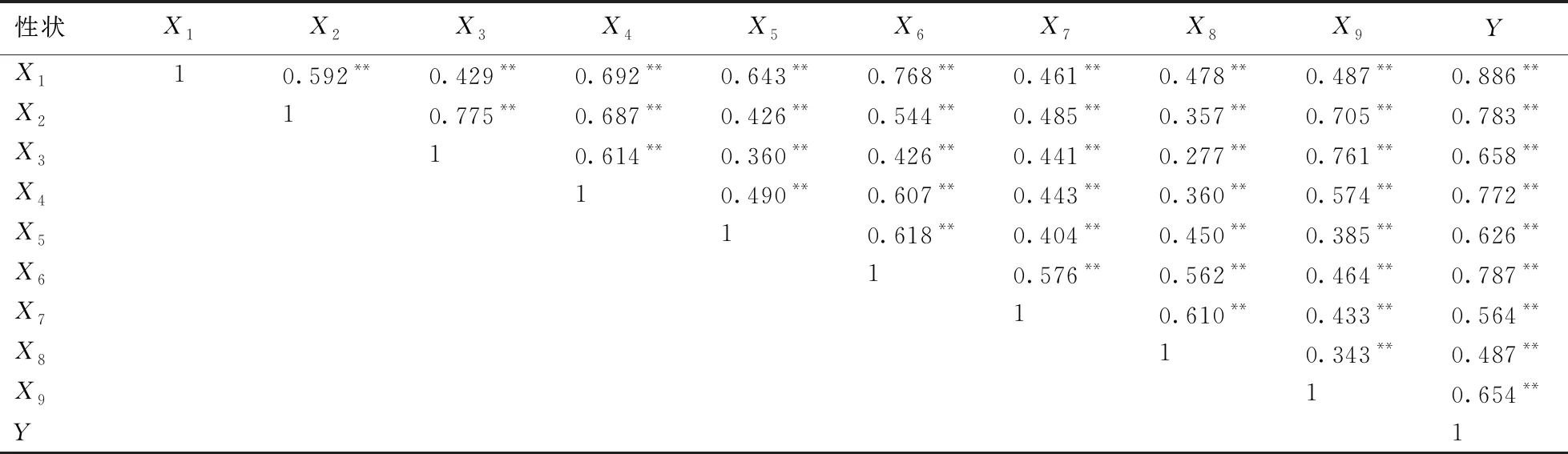
表2 性狀件表型相關系數

注： “*”表示相關性達到顯著水平(P< 0.05)，“** ”表示相關性達到極其顯著水平(P< 0.01)。

2.3 各性狀對體質量的影響分析

根據通徑分析原理，利用SPSS 19.0軟件得到各性形態狀對體質量的通徑系數，經顯著性檢驗，保留達到顯著水平的體長、體高、頭長、體寬和尾柄高5個性狀(表3)。結果顯示，體長對體質量的直接作用(0.515)最大，且大于其間接作用(0.370)，是影響體質量的主要因素，其他4個形態性狀對體質量的直接作用均小于間接作用，主要通過體長對體質量間接產生影響。

表3 各性狀對體質量影響的通徑分析

注： “*”表示性狀對體長的直接作用達到顯著水平(P<0.05)，“** ”表示相性狀對體長的直接作用達到極其顯著水平(P<0.01)。

2.4 各性狀對體質量的決定程度分析

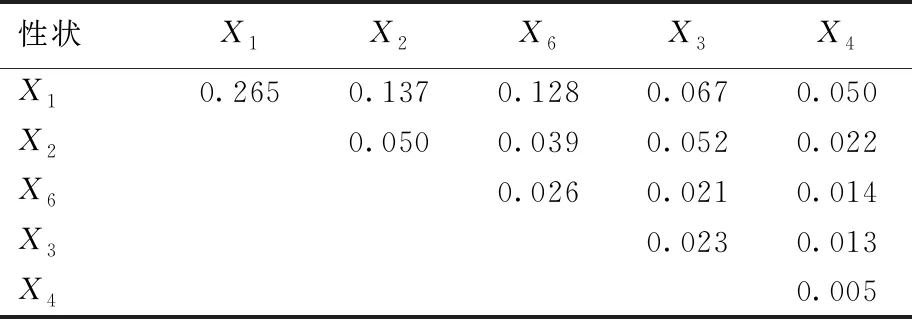
表4 各性狀對體質量的決定系數

根據公式計算出各性狀及性狀間協同對體質量的決定系數，結果見表4，其中單獨的決定系數中體長的決定程度最大，為0.265，尾柄高的的決定程度最小，為0.050；兩兩共同決定系數中，體長和體高的共同決定程度最大，為0.137，尾柄高和體寬的共同決定程度最小，為0.013。單獨的決定系數和兩兩共同決定系數的總合等于總的決定系數，5個性狀對體質量的總決定系數為0.912。

2.5 多元回歸方程的建立

運用SPSS線性多元回歸中的逐步回歸方式，剔除通徑系數檢驗不顯著的變量，對剩余變量建立以體質量為依變量的最優線性回歸方程：

Y= 0.079X1+0.107X2+0.103X3+0.092X4+0.094X5-5.474

其多元回歸分析的方差表、偏回歸系數和回歸常數的顯著性檢驗結果分別列于表5和表6。從表5可以看出，方程的回歸效果非常顯著(F=576.032，P=0.000<0.01)。表6的結果顯示體長、體高、頭長、體寬和尾柄高對體質量的偏回歸系數達到極其顯著水平，尾柄高對體質量的偏回歸系數達到顯著水平。經回歸預測，估計值與實際值差異不顯著(P>0.05)，說明該回歸方程可以應用于實際生產中。表7為多元回歸的復相關分析表，經過計算，體質量與體長、體高、頭長、體寬、尾柄高的復相關系數為0.956，調整決定系數為0.912，說明這5個形態性狀變量與體質量有極強的線性相關關系。

表5 多元回歸的方差分析

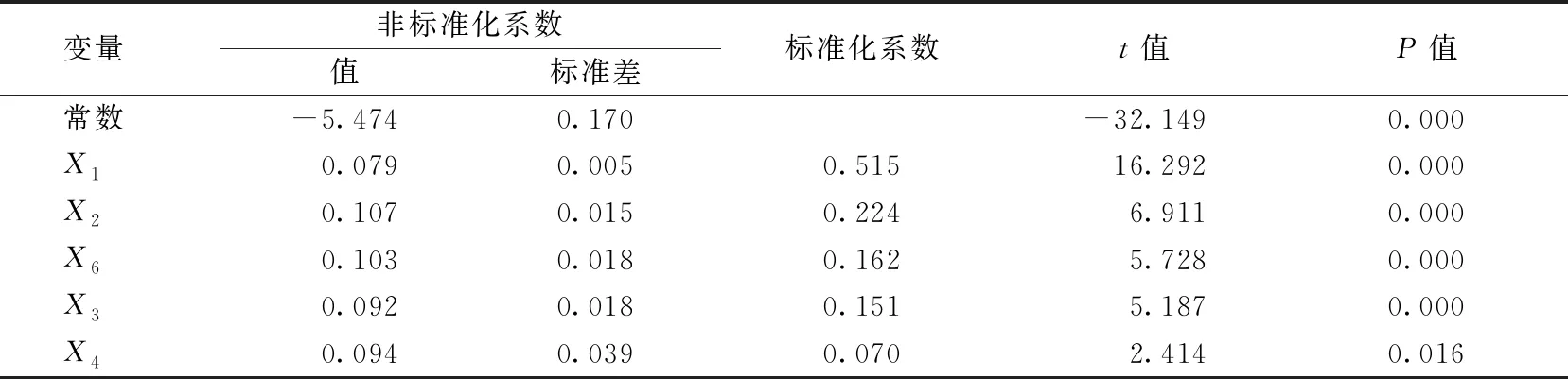
表6 回歸常數、偏回歸系數t檢驗結果

表7 多元回歸的復相關分析結果

3 討論

1)研究結果表明，試驗所測大鱗鲃各形態性狀與體質量的表型相關系數均達到極顯著水平(P<0.01)，其中體長、體高、頭長、體寬和尾柄高與體質量的相關系數相對較大，但由于并未排除其他變量的影響，因此不能準確反映體質量與體長等自變量之間的關系。采用相關系數、通徑系數、決定系數及多元回歸等綜合分析，進一步探討各形態性狀與體質量的真實關系。通徑分析和多元回歸的結果一致表明，體長、體高、頭長、體寬和尾柄高是影響大鱗鲃質量的主要性狀，這5個自變量的共同決定系數為91.2%。在多元回歸分析中，當復相關系數或者各自變量對因變量的單獨決定系數及兩兩共同決定系數的總和∑d(在數值上R2= ∑d)≥0.85時，說明該自變量是影響因變量的主要自變量[23]。研究中，R2= ∑d= 0.912>0.85，說明體長、體高、頭長、體寬和尾柄高是主要自變量，能在較大程度上影響體質量，其變化也更能說明體質量的變化趨勢。本研究通過相關分析、通徑分析和多元回歸分析，剔除了偏回歸系數不顯著的形態性狀，確定了影響大鱗鲃體質量的主要形態性狀，為選擇育種提供了科學依據和理想的測定指標，可用于指導大鱗鲃的選育工作。

2)目前，對于大鱗鲃的外部形態及內部消化器官已有深入研究，進而對其生物學特性、食性都有了進一步研究，為大鱗鲃的種質判別提供了理論依據[11]。然而，尚未有關于其體質量與形態相關性狀之間的相關性研究。體質量作為經濟魚類選育最直接最重要的目標性狀，也是生產性能的直接反映，然而體質量與形態性狀相比不直觀，且準確測量操作難度大，為選育增加了難度，由于基因連鎖及基因多效性的存在，生物體各個性狀間存在著不同程度的相關性，因此選擇與體質量相關性較高的形態性狀作為選育指標，可大大降低選育難度。本研究采用通徑分析及多元分析等方法，探討了大鱗鲃體質量和其他形態性狀間的關系，經篩選確定體長、體高、頭長、體寬和尾柄高為體質量的主要影響性狀，在選育時，操作過程更為簡便，并且可以有效避免單獨以體質量為指標造成的系統性誤差[27]。

3)大鱗鲃是一種具有廣闊市場前景的經濟魚類，選育工作對其人工養殖技術發展至關重要。建立了以大鱗鲃體質量為因變量，以體長、體高、頭長、體寬和尾柄高為自變量的最優多元回歸方程，在實際生產中，使用該方程可提高選育效率。對1齡大鱗鲃可達到較好的選育效果，針對其他生長階段的大鱗鲃選育，應重新構建多元回歸方程進行分析[28]。