以問題為導向的數學創新意識培養

白凌曉

《義務教育數學課程標準（2011年版）》新增了“創新意識”這一核心概念，并且指出“創新意識的培養是現代數學教育的基本任務，應體現在數學教與學的過程之中”，“創新意識的培養，應該從義務教育階段做起，貫穿數學教育的始終”。那么，在日常的小學數學課堂上，如何培養學生的創新意識呢？

數學是具備高度創造性的學科，無論是命題的歸納、邏輯的演繹、公式的推導、習題的演算都充滿著創新性。小學數學課堂教學應把樹立“問題意識”作為培養學生創新意識的重要抓手。教師應引導學生通過數學知識的習得、數學命題的推證、數學素質的生活運用等途徑發現新問題、求證新問題，為學生終身學習及未來職業生活打下堅實的基礎。

一、觀察試驗，引發猜想

教師在數學教學中有意識設計供學生觀察試驗、猜想命題、尋找規律的練習，能發展學生的創造性思維。如：一年級下冊《找規律》的“做一做”中給出的涂色、填數、擺放、填畫等都是有一定規律的，教師可以引導學生從顏色、聲音、數量、大小、形狀、數字關系、方向及其他性質著手發現直觀的規律，如果學生能進一步發現抽象而隱蔽的規律——圖形的排列有什么規律，數字的排列就有相應的變化規律，則說明學生的創造性思維上升了一個高度，也就種下了創新意識的一顆種子。

二、數形結合，萌生構想

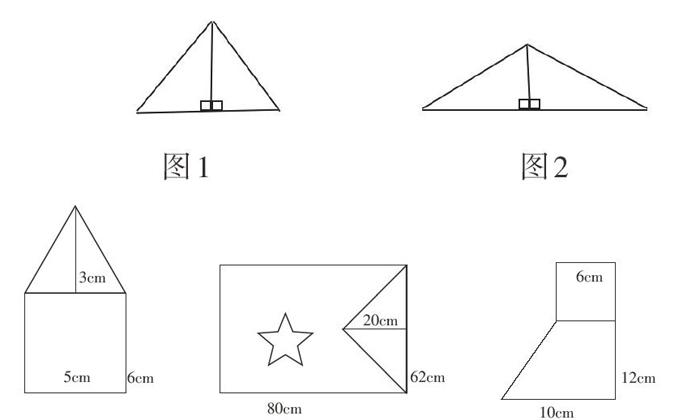
數學教學中，抓住數形結合，引導學生從幾何角度去看代數問題，或者從代數角度看幾何問題，是培養創造性想象力的有效途徑。教學四年級下冊的《三角形的內角和》時，首先以“數”構“形”：學生通過測量，得出三角形的內角和可能是180°。究竟是不是180°呢？教師引導學生通過剪（撕）、拼，將三角形的三個內角轉化成平角，運用幾何直觀，揭示問題本質。第二，以“形”思“數”：學生通過剪長方形、正方形，由已知長方形、正方形的內角和計算出三角形的內角和是180°。第三，數形相依，各展其長。用兩個完全一樣的直角三角形拼成一個大的銳角三角形（圖1），這個大的銳角三角形的內角和是180°×2-180°=180°，同理推出鈍角三角形（圖2）的內角和同樣是180°。

三、發散求異，多方設想

發散思維能力有助于學生提出新問題，孕育新思想，建立新概念，構筑新方法。在數學教學中，一題多解是培養學生發散思維、發展學生數學創造性思維的一條有效途徑。如：五年級上冊《多邊形面積的整理和復習》，在“課前小研究”教學活動中，教師設計“我會編”環節，讓學生自編一道關于組合圖形面積的問題并解答。學生設計出了如下圖所示的三幅組合圖形。

學生在解決平面組合圖形面積中，無論是運用分割、平移，還是采取轉化、補全等各種方法，實則離不開“等積變形”的數學思想，而通過自主設計和計算求解，學生的思維由發散到聚合，由直觀到深刻。

四、直覺頓悟，突發奇想

數學直覺是對數學對象的某種直接領悟或洞察。在小學數學教學中可以從估一估、猜一猜、整體把握等方面去創設情境，誘發直覺。如：“今有雞兔同籠，上有三十五頭，下有九十四足，問雞、兔各幾只？”這樣的問題。《孫子算經》中是這樣解答的，假如砍去每只雞、每只兔一半的腳，則每只雞就變成了獨角雞，每只兔就變成了雙腿兔。這樣雞和兔的腳的總數就由94只變成了47只。如果籠子里有一只兔子，則腳的總數就比頭的總數多1，因此，腳的總只數47與總頭數35的差，就是兔子的只數。這一思路新穎而奇特，一般小學生并不一定能夠想得到，需要教師在教學時做有效的引導。

五、群體智力，民主暢想

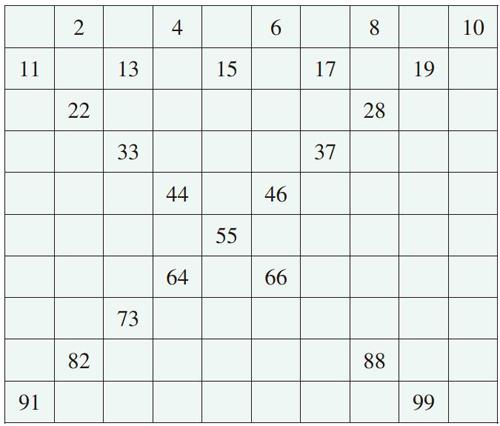
良好的教學環境和學習氣氛有利于培養學生的創造性思維能力。課堂上，教師對學生講授解題技巧是縱向交流、垂直啟發，而學生之間的相互交流和切磋則可以促進個體之間創造性思維成果的橫向擴散或水平流動。如一年級下冊“百數表”的教學，教師讓學生通過填“百數表”中的數，找出數的排列規律（如右圖）。

通過討論交流，學生構建起數與數之間的邏輯關系，清楚地掌握了100以內數的排列順序，探究出百數表中隱含的諸多規律。如：第一橫行的5個數都是雙數，第二橫行的5個數都是單數;從左上到右下這一斜行中的數（11、22、33、44……）個位、十位數字都相同;從右上到左下一行數中（10除外），十位上的數從1開始，逐漸多1直到9，而個位上的數則相反，從9開始逐漸少1直到1，等等。

以上幾點可操作性的方法，教師在采用時應因時、因地、因內容、因對象而異。只有綜合得當地融入自己的教學設計，才能收到預期的效果。

（作者單位：襄陽市教育科學研究室）