鲇魚山灌區渠首除險加固輸水能力研究

張文峰，李西平，黃紹磊，李 璐

（1.河南省水利勘測設計研究有限公司，河南 鄭州450016；2.河南省水利勘測設計協會，河南鄭州450016）

1 工程概況

鲇魚山灌區取水樞紐位于河南省商城縣鲇魚山水庫大壩下游4 km的灌河河道上，灌區設計灌溉面積9.53萬hm2。現狀渠首由進水閘、沖沙閘、溢流壩（堰）等建筑物組成。進水閘最大流量為119.2 m3／s，沖沙閘最大流量為728 m3／s，溢流壩原規劃最大輸水流量為3 940 m3／s。鲇魚山灌區取水樞紐運行40 a來，為灌區提供了充足水源，促進了灌區耕作制度和種植結構調整，帶動了相關產業快速增長。但受當時社會發展水平制約，原設計閘墩、底板配筋不能滿足現行規范要求。

2 原設計方案的問題

鲇魚山灌區取水樞紐1970年開始動工，1976年正式建成。查閱當年竣工資料，其進水閘、沖沙閘中墩和底板配筋均為Φ16＠300，滿足當時規范［1］中受拉、偏心受壓構件的受拉鋼筋最小配筋率（0.15%）的要求，但按照當前有效規范《水工混凝土結構設計規范》（SL／T 191—2008）［2］，受拉、偏心受壓構件的受拉鋼筋最小配筋率為0.2%，相應該工程中墩配筋應為Φ20＠200，底板配筋應為Φ25＠200。因此，原設計閘墩、底板配筋不能滿足現行規范要求。

其壅水計算采用天然河道一維恒定非均勻流方法，起推水位為溢流壩前水位，5 a一遇設計洪水位為78.2 m，依據最新實測河道資料，經過計算，5 a一遇洪水對應淹沒點水位為79.34 m，而淹沒點岸邊高程僅為78.4 m，當發生小頻率洪水時，易發生回水倒灌，發生漫溢。經初步統計，當發生5 a一遇洪水時，淹沒面積約2.8 km2，受災人口500余人、房屋700多間，連接鲇魚山水庫管理所與商城縣縣城的公路亦將遭受淹沒，影響水庫運行管理、調度和周圍百姓正常生活。

鑒于原設計的問題，2017年河南省水利廳組織有關專家對其進行了安全鑒定，基于河南省水利勘測設計研究有限公司的《鲇魚山灌區取水閘樞紐工程安全評價報告》及安全鑒定結論，本文對其除險加固后渠首的輸水能力進行了研究。

3 除險加固方案

鲇魚山灌區取水樞紐工程主要技術參數不能滿足規范要求，安全等級為C級，依據《水閘安全評價導則》安全類別評定標準，渠首樞紐閘鑒定為四類閘，需報廢重建［3］。

由于原渠首布置合理，建成之后各個建筑物過流能力正常［4］，因此除險加固的思路是：原平面布置不變，對進水閘、沖沙閘進行拆除重建；為解決發生低頻率洪水時出現回水倒灌的問題，新建左岸泄洪閘；同時新建檢修交通橋。

除險加固渠首平面布置見圖1。

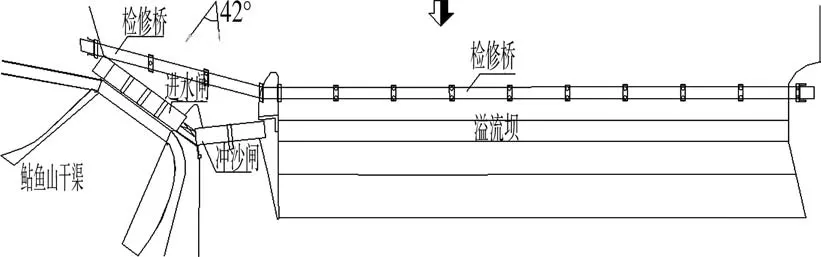
圖1 灌區除險加固渠首平面布置

該灌區溢流壩結構安全鑒定為B級，需進行裂縫處理，堰頂高程為77.47 m，上游設計水位為 81.92 m，堰前水深為4.45 m（見圖2）。新建檢修橋距溢流壩上游12 m，橋寬6 m，橋梁跨度20 m，即每兩節溢流壩分縫處設置一個橋墩，下部橋墩為圓形結構，直徑1 m。所建的橋梁連接樞紐左右岸，為方便兩岸連接及減小其對建筑物結構和過流的影響，所建橋梁在樞紐右岸溢流壩與沖沙閘交界處設一折線，其折線在裹頭處完成。

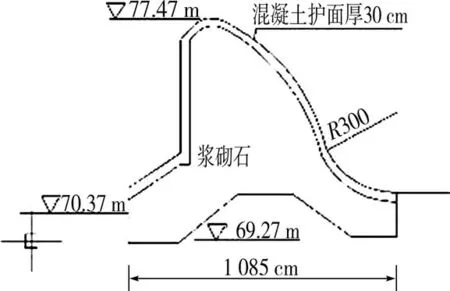
圖2 溢流壩斷面

新修檢修橋距離堰前12 m，約為堰頂水頭的2.68倍，不滿足距上游堰壁3～4倍堰前水頭的要求［5］。在堰前水頭影響范圍內建設橋梁對溢流壩輸水能力的影響目前少有研究，有必要進行深入分析。

4 輸水能力計算分析

鲇魚山灌區溢流壩的堰前水頭不包括行近流速水頭［5］。根據該溢流壩設計結構，堰頂寬度δ為3.2 m，設計堰頂水頭 H 為 4.45 m，δ／H＝0.72，0.67＜δ／H＜2.5，結合設計形態（圖2），可判別其為曲線形實用堰。雖然曲線形實用堰的輸水能力計算有常規的理論計算公式，但常規理論計算要求的邊界條件一般很難保證。根據鲇魚山灌區取水樞紐新修檢修橋后的情況，對其輸水能力計算采用了常規水力計算、非均勻流計算、水動力數值模擬計算3種方法，以便相互對比、驗證。

4.1 常規水力計算

檢修橋設在溢流壩上游，結合該工程實際情況，根據堰頂寬度和最大輸水能力對應的堰前水深，溢流壩流態為實用堰流態，輸水能力按照《溢洪道設計規范》中公式［6］計算。經計算，建橋前溢流壩實際最大輸水流量為4 241 m3／s；將橋梁建在溢流壩上后，溢流壩最大輸水流量為3 816 m3／s。

4.2 非均勻流計算

首先按天然河道為非均勻流計算上游橋梁阻水引起的水位落差，然后根據水位降落后的數值，按溢洪道設計規范推薦的公式計算溢流壩輸水能力。計算得到溢流壩最大輸水流量為4 100 m3／s，比建橋前的（實際最大輸水流量4 241 m3／s）略小。

4.3 水動力數值模擬計算

溢洪道水流問題和水利樞紐的水流問題，常需制作水力模型進行研究［7］，這是解決復雜工程課題的重要手段。但模型試驗一般難以滿足全部相似條件，且模型制作成本高，時間周期長。隨著科學技術的進步，許多模型試驗可以采用計算機數值模擬來替代，采用數值模型是對傳統物理模型的豐富和補充，同時可大大提高效率、降低成本。筆者采用數值模擬方法對建橋后的溢流壩水力特性進行了研究。

4.3.1 基本控制方程

基本控制方程［8］為連續性方程、動量守恒方程和k-ε方程。

連續性方程為

式中： xi為坐標分量（ i＝ 1，2，3）；ui為速度分量。

動量守恒方程為

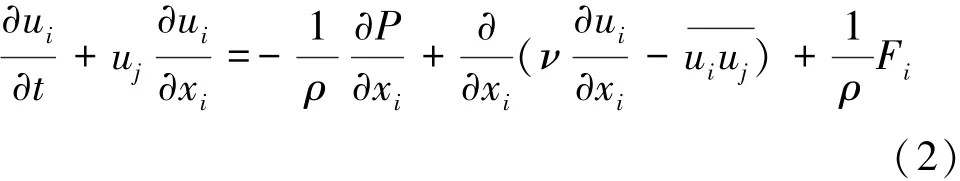
式中：uj為流體的速度分量；t為時間；P為平均壓力；ρ為水的密度；ν為流體的運動黏度；Fi為作用于單位質量水體的體積力。

k-ε方程如下：

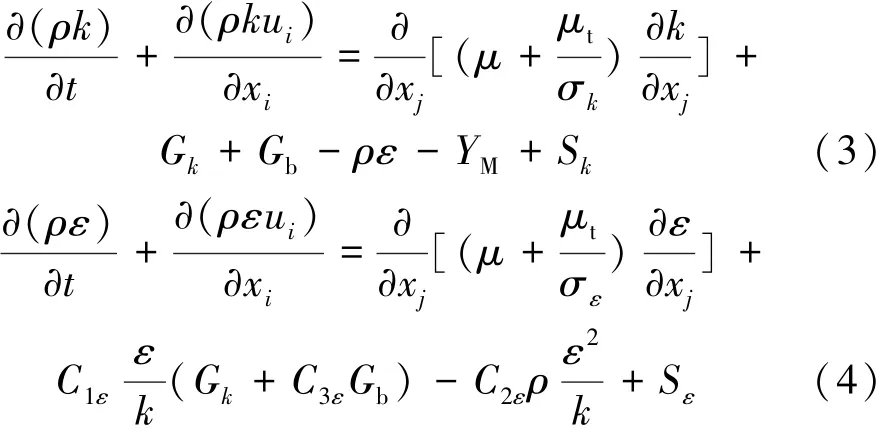
式中：k為紊動能；μ為黏性系數；xj為坐標分量；ε為耗散率；σk、σε為湍動能和耗散率下普朗特數；Gk為平均速度梯度引起的湍動能；Gb為浮力引起的湍動能；YM為可壓縮湍流脈動膨脹對總耗散率的影響；Sk、Sε為用戶定義的源項；μt為湍流黏度； C1ε、 C2ε、 C3ε為模型常數。

4.3.2 計算方法

計算方法采用當前水力學應用較為廣泛的有限體積法，該方法是求解不可壓縮、黏性、瞬變和具有自由面流動的流體特性的一種數值方法。計算時對每一相引入體積分數變量αq，通過求解每一控制單元內體積分數值確定相間界面。

計算中所有控制單元表面體積通量的計算采用隱式差分格式，即

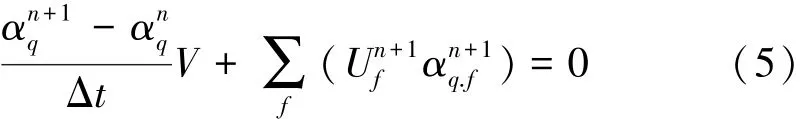
式中：n+1為當前時間步指示因子，n為前一時間步指示因子；t為時間；αq.f為單元表面第q相體積分數計算值；V為控制單元體積；Uf為控制單元表面體積通量。

離散格式采用二階迎風格式，壓力 -速度耦合采用壓力校正法，時間差分采用全隱格式。

4.3.3 計算區域、邊界及網格劃分

數值模擬計算區域包括上游河道（長170m，距壩軸線170m斷面為模型上游邊界）、溢流壩、沖沙閘、進水閘、消力池、海漫、防沖槽、下游河道（長200m，距壩軸線200m斷面為下游邊界），分為建橋前和建橋后兩種模擬工況，建橋前計算模型見圖3。根據工程實際，分析了多種水位組合后確定以對工程防洪作用意義較大的設計水位為典型進行分析，設計上游水位為 81.92m，相應下游水位為79.0m，河道和建筑物邊界采用無滑移邊界。

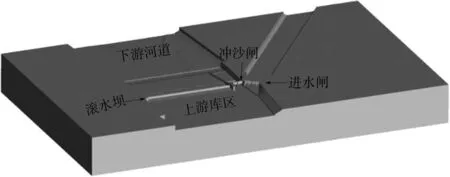
圖3 建橋前計算模型

由于該工程在空間上相對比較規則，網格劃分選擇一般結構網格，上、下游河道和建筑物均采用立方體網格，溢流壩、水閘網格長度為0.25m，上、下游河道網格長度為1m，網格總數約1170萬個。

4.3.4 水力模擬輸出結果

本次數值模擬采用的是整體水利樞紐模型，可以得出各個建筑物在不同重現期時數值模擬計算結果，其中50a一遇洪水時各建筑物數值模擬輸水能力見表1。

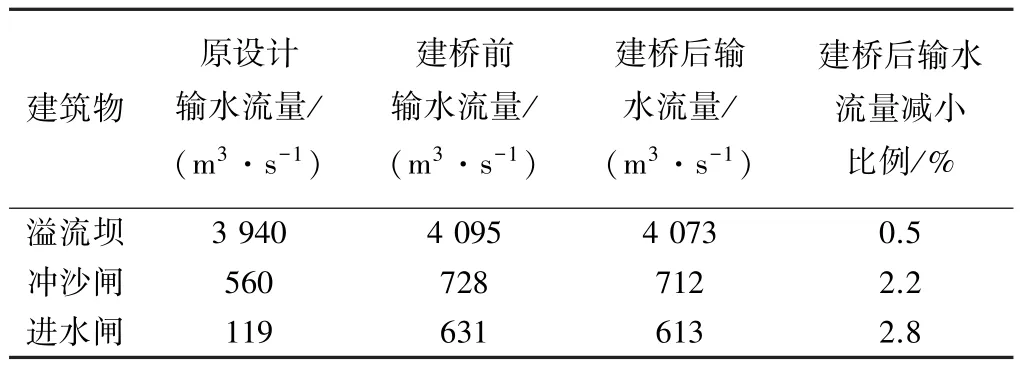
表1 各建筑物數值模擬輸水能力對比

由表1可知，雖然建橋后各個建筑物輸水能力有不同程度的衰減，但衰減率均小于3%，因此仍能滿足原設計過流能力要求。

5 綜合分析

將溢流壩公式計算、非均勻流計算以及數值模擬計算輸水能力進行對比分析，見表2。

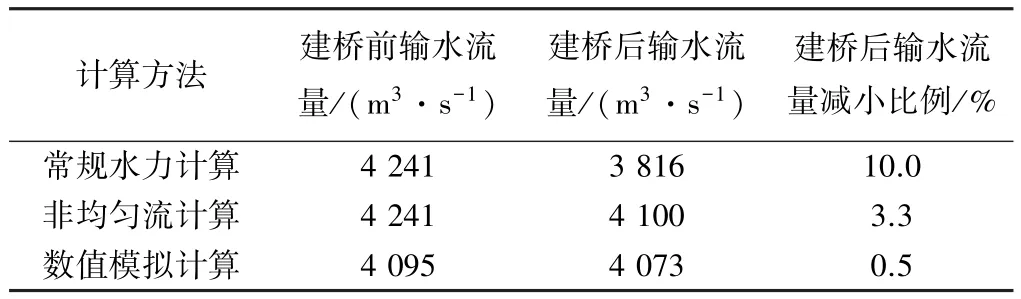
表2 溢流壩公式計算、非均勻流計算及數值模擬計算結果對比

常規水力計算的優點在于所得數值具有普遍性，但該工程溢流壩輸水流量常規水力計算值是在假設將橋梁修建在溢流壩上計算的，其結果只能作為對其他計算方法的參考。

按非均勻流計算溢流壩輸水能力時，其堰上水頭來源有理論依據，但其水頭不能滿足一般堰流計算的要求，尚缺少理論支撐，其結果亦只能作為參考。

水動力數值模擬計算相當于采用數值方法進行了一次模擬試驗，計算區域相對較大，邊界條件與實際情況更為接近。數值模擬結果大于公式計算結果、小于非均勻流計算結果，認為將其作為設計依據更加合理。

根據已建好的數值模型及其邊界條件，繼續研究了在溢流壩上游不同位置（0、4、8、12m）建橋時對溢流壩輸水能力的影響，結果見表3。

可見，在溢流壩上游0m建橋時，橋墩減小了過流面積，輸水流量變化較大；在溢流壩上游4、8、12m建橋時，對輸水流量的影響逐漸減弱，在溢流壩前12m建橋對溢流壩過流能力的影響最小。

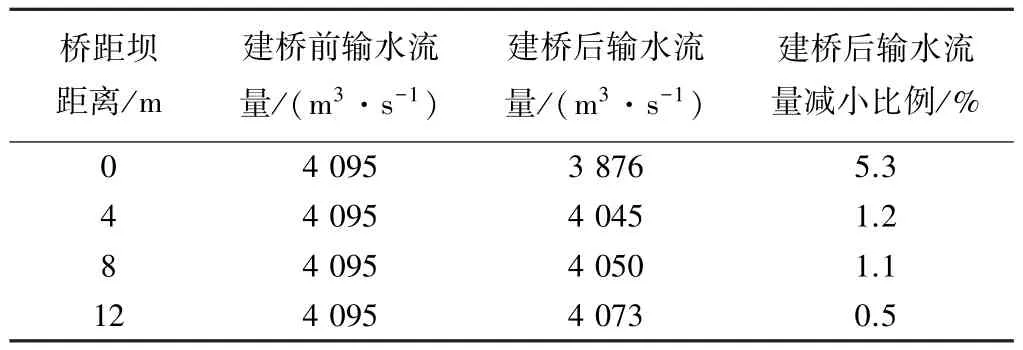
表3 不同橋位下溢流壩過流能力數值模擬結果

6 結 語

鲇魚山灌區取水樞紐原設計閘墩、底板配筋不能滿足現行規范要求，當發生小頻率洪水時，易發生回水倒灌，淹沒樞紐上游2.6 km處河道右岸地勢較低的農田、道路，樞紐建筑物之間缺少檢修維護交通橋。除險加固選擇對進水閘、沖沙閘進行拆除重建，為解決發生低頻率洪水時出現回水倒灌的問題，提出了新建左岸泄洪閘，同時新建檢修交通橋。根據鲇魚山灌區渠首樞紐除險加固的實際情況，對樞紐建筑物輸水能力進行了研究。分析表明：雖然建橋后各個建筑物的輸水能力都有不同程度的衰減，但衰減率均小于3%，因此仍能滿足原規劃過流能力要求；在溢流壩前12 m位置建橋對大型灌區樞紐溢流壩的過流能力影響最小。