逐次Taylor替換與一類冪指函數不等式的機器證明

陳世平，陳 果

（1.中國民航飛行學院德陽校區-四川省商貿學校，四川 德陽 618000；2.西南科技大學信息工程學院，四川 綿陽 612000）

0 引 言

Nishizawa 證明了[10]：

Branko Male?evic 等證明了文獻[10]提出的公開問題[11]：

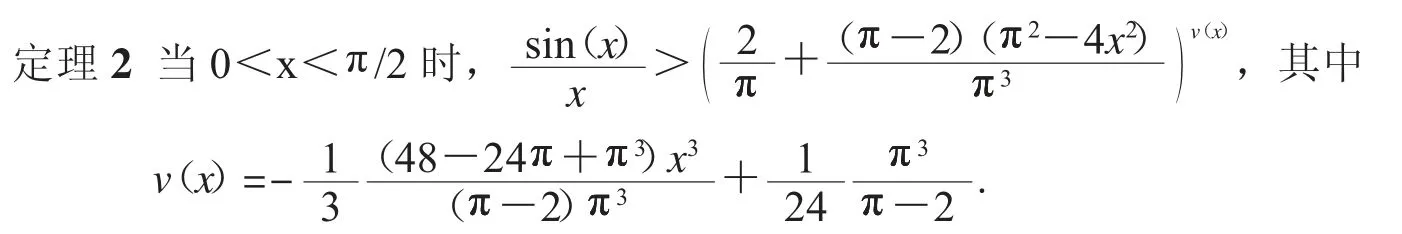
文獻[12-17]討論了形如f（x，trans1（x），…，transn（x））＞0 的超越多項式不等式的機器證明，其中f（x，x1，…，xn）是n＋1 元多項式，trans1（x）可以是初等超越函數，如sin x、cos x、tan x、arcsin x、arccos x、arctan x、ex、ln x 等，也可以是形如trans1（trans2（x））的復合函數，利用一次或多次Taylor 替換，目標不等式的證明轉化為一系列單變量的多項式不等式的驗證，然后由代數不等式證明軟件BOTTEMA 完成.算法對于常見的超越多項式不等式非常有效，而且是“可讀的”，可以輸出能夠理解的證明過程.這種方案被稱為逐次Taylor 替換法.

本文的目的是討論定理2 中不等式的機器證明，這是一個比文獻[12-17]中引用的例子更復雜、超越多項式不等式范圍外形如sin（x）/x＞u（x）v(x)的冪指函數不等式問題，運用逐次Taylor 替換并結合人工證明和巧妙的變量代換，實現了該不等式的機器證明.通過與文獻[11]不同的途徑，也證明了文獻[10]提出的公開問題，盡管結論是已知的結果，但方法本身對于同類不等式具有示范性.

此外，算法輸出的證明過程中除了有的需要判定其正定性的一元有理多項式次數較高從而驗證計算量較大外，其余內容都容易“手工”驗算.

1 逐次Taylor替換

不等式的自動證明問題，一直以來都是數學機械化和自動推理領域研究熱點和難點問題.近年來，代數不等式的自動證明吸引了大批學者研究，也取得了豐富的成果，已有專著《不等式機器證明與自動發現》問世，特別是楊路教授提出了降維算法，據之編制的通用程序BOTTEMA 能夠成批驗證不等式，但BOTTEMA 只能處理代數不等式或先把幾何不等式轉化為代數不等式，尚不能解決一般的超越不等式自動證明問題[18-22].當然關于超越不等式已有了大量的研究成果和證明方法，但這些成果和方法尚不能適應數學機械化和推理自動化的需要，故有必要對此類不等式的自動證明進行專門的研究，探索新的算法.

1.1 Taylor替換

給定（n＋1）元實系數多項式環R[x，x1，…，xn]，定義該環上一個映射：hom:f（x，x1，…，xn）→F（x），將變量xi用某個超越函數transi（x）代替.

定義1.1 給定（n＋1）元實系數多項式f（x，x1，…，xn），它在映射hom 下的像F（x）=hom（f）=f（x，trans1（x），…，transn（x））稱為超越函數多項式，稱transi（x）為其超越因子.

如x＋sin（x）、x＋cos（sqrt（x））、x＋esin(x)、x＋arctan（x）-arcsin（x）都是超越函數多項式，sin（x）、cos（sqrt（x））、esin(x)、arctan（x）、arcsin（x）就是函數的超越因子.

定義 1.2 對于超越函數 F（x），在某個區間 I，如果有代數函數列{T_min（n，F）}和{T_max（n，F）}，存在自然數 n0，當 n≥n0時，滿足：

1）T_min（n＋1，F）＞T_min（n，F），且當 n→∞ 時，T_min（n，F）→F（x）；

2）T_max（n＋1，F）＜T_max（n，F），且當 n→∞ 時，T_max（n，F）→F（x）.

我們稱{T_min（n，F）}和{T_max（n，F）}為 F（x）在區間 I 的下限多項式列和上限多項式列，T_min（n，F）為 F（x）的下限多項式，T_max（n，F）為 F（x）的上限多項式，n0稱為臨界值.

顯然，F（x）的下限多項式和上限多項式滿足：

T_min（n0，F）（x）＜T_min（n0＋1，F）（x）＜T_min（n0＋2，F）（x）＜…＜F（x）＜…＜T_max（n0＋2，F）（x）＜T_max（n0＋1，F）（x）＜T_max（n0，F）（x），也就是說若 F（x）存在有下限多項式列和上限多項式列，則有一個多項式套來逼近 F（x）:（T_min（n0，F）（x），T_max（n0，F）（x））?（T_min（n0＋1，F）（x），T_max（n0＋1，F）（x））?（T_min（n0＋2，F）（x），T_max（n0＋2，F）（x））?……?{F（x）}.

下面我們討論如何計算或構造超越函數多項式F（x）=f（x，trans（x））的下限多項式和上限多項式（其中f（x，y）為二元多項式）.

為方便，我們將函數f（x）在0 點的Taylor 展開式中的前n 項之和記為taylor（f，n）.

定義1.3 如果超越函數f（x）在某個區間（0，T］滿足以下條件：（1）大于0；（2）在0 點的Taylor 展開式收斂于f（x）；（3）taylor（f，n）可以表示為交錯級數f1（x）-f2（x）＋f3（x）＋…＋（-1）n-1fn（x），其中fn（x）=An*x＾mn，0＜An≤1，mn-1＜mn；（4）存在常數n0，當n≥n0時，taylor（f，n）＞0，fn（x）＞fn＋1（x）＞0.我們稱f（x）在區間（0，T］內可以規范展開，常數n0稱為其臨界值.若還滿足An≤1/（n-1）!，則稱f（x）在區間（0，T］內可以強規范展開.

常見的基本初等超越函數大都可以在相應的區間內規范展開：

arctan（x）=x-x3/3＋x5/5-x7/7＋…＋（-1）n-1x2n-1/（2n-1）＋……在區間（0，1］可以規范展開，臨界值n0=1；

e-x=1-x＋x2/2!-x3/3!＋…＋（-x）n-1/（n-1）！＋……，在區間（0，T］（T 為任意正數，下同）可以規范展開，臨界值n0=min{n∈N，當0＜x≤T 時taylor（e-x，n）＞0，taylor（e-x，n＋1）＞0，n＞T}；

ln（1＋x）=x-x2/2＋x3/3-……＋在區間（0，1］可以規范展開，臨界值n0=1；

sin（x）=x-x3/3!＋x5/5!-……＋在區間（0，T］可以規范展開，其中臨界值n0=min{n∈N，當0＜x≤T 時taylor（sin（x），n）＞0，taylor（sin（x），n＋1）＞0 且2n（2n＋1）＞T2}，特別地，當時，n0=1；

cos（x）=1-x2/2!＋x4/4!-……＋在區間（0，T］可以規范展開，其中臨界值n0=min{n∈N，當0＜x≤T 時taylor（cos（x），n）＞0，taylor（cos（x），n＋1）＞0 且 2n（2n-1）＞T2}.我們注意到，當時，taylor（cos（x），2n）＜cos（x）=0，所以 cos（x）在內不能規范展開；

（1＋x）a=1＋ax＋a（a-1）x2/2!＋a（a-1）（a-2）x3/3!＋C（a，n）xn＋…，在區間（0，1）可以規范展開（其中 C（a，n）=a（a-1）（a-2）…（a-n＋1））.當 0＜a＜1 時，n0=1（展開式中f1（x）=1＋ax）.

其中 e-x、sin（x）、cos（x）在相應區間內還可強規范展開.

也有一些基本初等超越函數不能規范展開，如：

ln（1-x）=-x-x2/2-x3/3-……-xk/k-……（0＜x＜1）；

tan（x）=ΣB2n（-4）n（1-4n）x(2n-1)/（2n）!=x＋（1/3）x3＋（2/15）x5＋（17/315）x7＋（62/2835）x9＋……

引理1.1 如果f（x）區間I 可以規范展開，臨界值為n0，則當n＞n0時，在區間I 上

1）taylor（f，2n-2）＜taylor（f，2n）＜f（x）；

2）taylor（f，2n-1）＞taylor（f，2n＋1）＞f（x）；

3）當n→∞時，taylor（f，n）→f（x）.

為方便，引入如下記號：

acrtan_max（x，n）=taylor（arctan（x），2n＋1），arctan_min（x，n）=taylor（arctan（x），2n），則當 x∈（0，1］，對任意 n∈N，arctan_max（x，n）＞arctan（x）＞arctan_min（x，n）；

ln_max（x，n）=taylor（ln（1＋x），2n＋1），ln_min（x，n）=taylor（ln（1＋x），2n），則當x∈（0，1），對任意 n∈N，ln_max（x，n）＞ln（1＋x）＞ln_min（x，n）；

sin_max（x，n）=taylor（sin（x），2n＋1），sin_min（x，n）=taylor（sin（x），2n），則當x∈對任意 n∈N，sin_max（x，n）＞sin（x）＞sin_min（x，n）；

cos_max（x，n）=taylor（cos（x），2n＋1），cos_min（x，n）=taylor（cos（x），2n），則當對任意 n∈N，cos_max（x，n）＞cos（x）＞cos_min（x，n）；

用f＋和f-分別表示多項式f 展開后的正項和負項之和，顯然f=f＋＋f-，并且下面的引理成立：

引理1.2 假設實函數T1（y）＞0，T2（y）＞0 且T1（y）＜x＜T2（y），則

f＋（T1（y），y）＋f-（T2（y），y）＜f（x，y）＜f＋（T2（y），y）＋f-（T1（y），y）.

定理1.1 F（x）=f（x，trans（x）），trans（x）在區間I 可以規范展開，則對任意n∈N，

T_max（n，F）=f＋（x，taylor（trans（x），2n-1））＋f-（x，taylor（trans（x），2n））為 F（x）的上限多項式；

T_min（n，F）=f＋（x，taylor（trans（x），2n））＋f-（x，taylor（trans（x），2n-1））為 F（x）的下限多項式.

定理 1.2 設{T_min（n，F）}和{T_max（n，F）}分別是超越函數多項式 F（x）在區間 I 的下限多項式列和上限多項式列，則在相應區間內，

1）若存在 n0使得 T_min（n0，F）≥0 成立，則 F（x）＞0 成立；

2）若存在 n0使得 T_max（n0，F）≤0 成立，則 F（x）＜0 成立；

3）若存在 n0使得 T_max（n0，F）＞0 和 T_min（n0，F）＜0 都不成立，則 F（x）在區間 I的符號不固定.

上述方案運用Taylor 展開式構造超越函數多項式的上下限多項式列，建立一個逼近目標函數的一元多項式套，從而將目標不等式的證明轉化為一系列的一元多項式不等式的驗證，我們將這種方案稱為Taylor 替換法.

1.2 逐次Taylor替換

一般的超越函數多項式可能包含多個超越因子，超越因子可能還是由超越函數或代數函數復合而成，經過一次Taylor 替換后的函數可能還是包含超越因子，還需要再次甚至多次的Taylor 替換.我們以超越函數多項式F（x）=f（x，trans1（x），trans2（x））和F（x）=f（x，trans1（trans2（x）））為例來描述這個過程：

1、F（x）=f（x，trans1（x），trans2（x）），其中超越函數trans1（x）、trans2（x）在區間I 內可以規范展開，臨界值分別為n1、n2.

令f1（x，trans2（x），m）=f＋（x，taylor（trans1（x），2*m），trans2（x））＋f-（x，taylor（trans1（x），2*m-1），trans2（x））；

令f2（x，m，n）=f1＋（x，taylor（trans2（x），2*n），m）＋f1-（x，taylor（trans2（x），2*n-1），m）；

顯然當m＞n1時，f1（x，trans2（x），m）＜f（x，trans1（x），trans2（x）），當m→∞時，f1（x，trans2（x），m）→f（x，trans1（x），trans2（x））；

當n＞n2時，對任意m＞n1，f2（x，m，n）＜f1（x，trans2（x），m），當n→∞時，f2（x，m，n）→f1（x，trans2（x），m）；

即當m＞n1，n＞n2時，f2（x，m，n）＜f（x，trans1（x），trans2（x）），當m→∞，n→∞時，f2（x，m，n）→F（x）.

特別地，T_min（n，F）=f2（x，n，n）就是F（x）的下限多項式，{T_min（F，n）}是其下限多項式列，其臨界值n0=max{n1，n2}.

類似的方法可以求得F（x）的上限多項式列.

同樣的方法我們可以計算含更多“超越因子”形如f（x，trans1（x），trans2（x），trans3（x），…，transm（x））的超越函數的上下限多項式列.

2、F（x）=f（x，trans1（trans2（x））），其中trans2（x）在區間I 可以規范展開，其臨界值為n2，trans2（x）在區間I 上的值域為區間J，trans1（x）在J 內可以規范展開，其臨界值為n1.

令trans2（x）=u，得到F1（x，u）=f（x，trans1（u）），

令f1（x，m，u）=f＋（x，taylor（trans1（u），2m））＋f-（x，taylor（trans1（u），2m-1）），

顯然，當m＞n1時f1（x，m，u）＜F1（x，u）=f（x，trans1（u）），且當m→∞時，f1（x，m，u）→F1（x，u）；

若trans2（x）是代數函數，則f1（x，m，trans2（x））就是F（x）的下限多項式，否則

令f2（x，m，n）=f1＋（x，m，taylor（trans2（x），2n））＋f1-（x，m，taylor（trans2（x），2n-1）），

當n＞n2時，f2（x，m，n）＜f1（x，m，trans2（x））＜F（x）=f（x，trans1（trans2（x））），且當n→∞時，f2（x，m，n）→f1（x，m，trans2（x））；

從而當m→∞，n→∞時，f2（x，m，n）→F（x）=f（x，trans1（trans2（x）））.

特別地，T_min（F，n）=f2（x，n，n）是F（x）的下限多項式，{T_min（F，n）}是其下限多項式列.其臨界值n0=max{n1，n2}.

類似的方法可以求得F（x）的上限多項式列.

同樣的方法我們可以計算含形如trans1（trans2（trans3（x）））經過更多次復合而成的超越因子的超越函數的上下限多項式列.

我們把上述方案稱為逐次Taylor 替換，一個可以計算一般超越函數多項式f（x，trans1（x），…，transn（x））的上下限多項式列的逐次Taylor 替換過程可以遞歸地定義如下：

算法 1.1 STS（Successive Taylor Substitution）

輸入①超越函數多項式F（x）；②n∈N；

輸出F（x）的下（上）限多項式.

1）若 F（x）為代數函數

return[F（x），F（x）]；

算法結束；

2）設trans（x）是F（x）的一個超越因子且可以表示為F（x）=f（x，trans（x））

2.1）若trans（x）在相應區間可以規范展開，則

f1（x，n）←f＋（x，taylor（trans（x），2n））＋f-（x，taylor（trans（x），2n-1））；

T_min（n，F）←STS（f1（x，n））[1]；

f2（x，n）←f＋（x，taylor（trans（x），2n-1））＋f-（x，taylor（trans（x），2n））；

T_max（n，F）←STS（f2（x，n））[2]；

return[T_min（n，F），T_max（n，F）]；

2.2）若trans（x）具有形如trans1（trans2（x））的復合形式，令F（x）=f（x，trans1（u）），其中u=trans2（x），假設trans1（u）在相應區間可以規范展開.

f1（x，n，u）←f＋（x，taylor（trans1（u），2n））＋f-（x，taylor（trans1（u），2n-1））；

T_min（n，F）←STS（f1（x，n，trans2（x）））[1]；

f2（x，n，u）←f＋（x，taylor（trans1（u），2n-1））＋f-（x，taylor（trans1（u），2n））；

T_max（n，F）←STS（f2（x，n，trans2（x）））[2]；

return[T_min（n，F），T_max（n，F）]；

3）END.

算法STS 還不能直接處理類似tan（x）、ln（1-x）、ex這類不能規范展開的超越因子，在證明過程中需要結合人工證明和做一些的變量代換.

超越函數多項式的“超越因子”還可能就是超越常數，也需要有理化.本文的處理方法是將超越數視為一個超越函數，構造一個逼近該超越數的有理數端點區間套.比如對于超越數t，我們構造滿足如下性質的區間列{[t1（n），t2（n）]}：

1）t1（1）＜t1（2）＜…＜t1（n）＜…＜t＜…t2（n）＜…t2（2）＜t2（1）；

2）當n→∞時，t1（n）→t，t2（n）→t；

3）端點t1（n）和t2（n）均為有理數.

若f（x，t）是系數含超越數t 的一元多項式，則

T_max（n，f）=f＋（x，t1（n））＋f-（x，t2（n））為f（x，t）的上限多項式；

T_min（n，f）=f＋（x，t2（n））＋f-（x，t1（n））為f（x，t）的下限多項式.

輸入：n∈N；

輸出：有理數端點區間[t1（n），t2（n）]，滿足：對任意p≤n，t1（1）＜t1（2）＜…＜t1（p）＜＜t2（p）＜…＜t2（2）＜t2（1）；當n→∞ 時，t1（n）→，t2（n）→.

1）t1←16*subs（x=1/5，arctan_min（x，n））-4*subs（x=1/239，acrtan_max（x，n））；

2）t2←16*subs（x=1/5，acrtan_max（x，n））-4*subs（x=1/239，tarctan_min（x，n））；

3）return[t1，t2]；算法結束.

2 定理2的證明

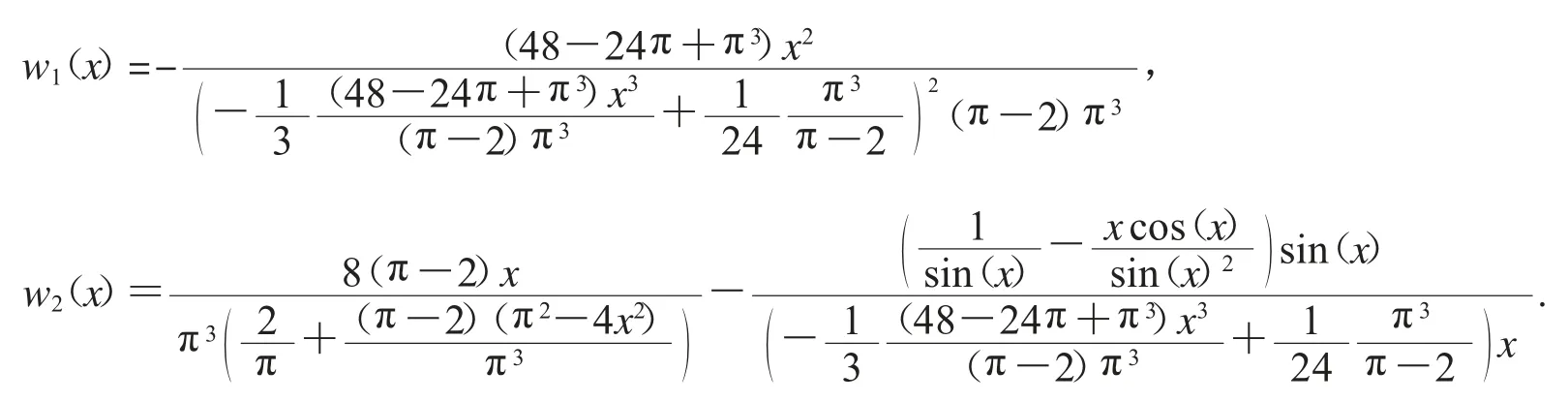
令f3（x）=numer（f2（x））*denom（f2（x））（其中numer（f（x））和denom（f（x））分別取分式的分子和分母，下同），顯然sgn（f2（x））=sgn（f3（x））.

令g1（x，n）=subs（ln（x/sin（x））=B（x，n），f3＋）＋subs（ln（x/sin（x））=A（x，n），f3-），則對任意n∈N，g1（x，n）＜f3（x）；

令g2（x，n）=numer（g1（x））*denom（g1（x））；

令g3（x，n）=subs（sin（x）=sin_min（x，n），g2＋）＋subs（sin（x）=sin_max（x，n），g2-），則對任意n∈N，g3（x，n）＜g2（x，n）；

令g4（x，n）=subs（cos（x）=cos_min（x，n），g3＋）＋subs（cos（x）=cos_max（x，n），g3-），則對任意n∈N，g4（x，n）＜g3（x，n），此時g4（x，n）還含有超越數作為系數；

令g5（x，n）=subs（=_to_ra（tn）[1]，g4＋）＋subs（=_to_ra（tn）[2]，g4-），則對任意n∈N，g5（x，n）是關于x 的一元有理多項式，且g5（y，n）＜g4（x，n）＜g3（x，n）＜g2（x，n）；

使用BOTTEMA 的xprove 指令：xprove（g5（x，n）＞0，[x＜_to_rat（n）[2]/3]）， 當n=5 時，不等式g5（x，n）＞0 成立，即當x∈（0，x＜_to_ra（t5）[2]/3）（0/3］，g2（x，5）＞0，從而f3（x）＞g1（x，5）＞0，繼而f2（x）＞0，得到f1（x）在（0/3］內單調上升.

證明f1（x）=-ln（u（x））-1/v（x）*ln（x/sin（x）），由于u（0）=1，v（0）=且當x→0＋，ln（x/sin（x））→0，所以當x→0＋，f1（x）→0.而由引理3.1，當x∈（0，/3］，f1（x）關于x單調上升，從而f1（x）＞0.

證明 令w3（x）=nume（rw1（x））*denom（w1（x）），得到

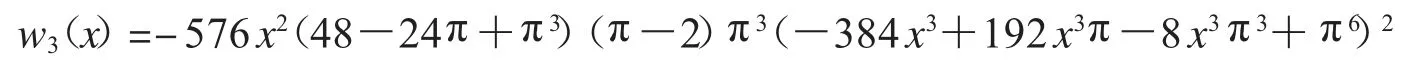
令w4（（x，n）=subs（=_to_ra（tn）[2]，w3＋）＋subs（=_to_ra（tn）[1]，w3-），則w4（x，n）是關于x 的有理多項式，且對任意n∈N，w4（x，n）＞w3（x）；

使用BOTTEMA 的xprove 指令：xprove（w4（x，n）＜0，[x＜_to_ra（tn）[2]/2]），當n=2 時，w4（x，n）＜0 成立，即在（0/2］內0＞w4（x，2）＞w3（x），從而w1（x）＜0.

證明 令f4（x）=-（ln（x/sin（x））＋w2（x）/w1（x）），由引理2.2 知，在（0，/2］內w1（x）＜0，所以在（/3，/2］內sgn（f4（x））=sgn（f2（x））.

令f5（x）=f4（`x），則f5（x）為包含x、sin（x）、cos（x）、的分式.由于 cos（x）在（/3，/2）內不能規范展開，作變量替換x=/2-y，則f5（x）＜0 在（/3，/2）內成立等價于在（0/6）內g（y）=f5（/2-y）＜0 成立.

令g1（y）=numer（g（y））*denom（g（y））；

令g2（y，n）=subs（sin（y）=sin_max（y，n），g1＋）＋subs（sin（y）=sin_min（y，n），g1-），則對任意n∈N，g2（y，n）＞g1（y）；

令g3（y，n）=subs（cos（y）=cos_max（y，n），g2＋）＋subs（cos（y）=cos_min（y，n），g2-），則對任意n∈N，g3（y，n）＞g2（y，n）；

令g4（y，n）=sub（s=_to_ra（tn）[2]，g3＋）＋sub（s=_to_ra（tn）[1]，g3-），則g4（y，n）是關于y 的一元有理多項式，且g4（y，n）＞g3（y，n）＞g2（y，n）＞g1（y）；

使用BOTTEMA 的xprove 指令：xprove（g4（y，n）＜0，[y＜_to_rat（n）[2]/6]）， 當n=8 時，不等式g4（y，n）＜0 成立，即在（0/6）內g1（y）＜0 成立，g（y）＜0 成立.從而在（/3/2）內f5（x）＜0 成立.由此得到f4（x）在（/3/2）內單調下降.

下面討論f2（/2）的符號.令

h1=nume（rf2（/2））*denom（f2（/2））=其中和ln（/2）需要有理化，令t=/2-1，則 t∈（0，1），ln（1＋t） 可以規范展開，即對任意 n∈N，ln_max（t，n）＞ln（1＋t）=ln（/2）＞ln_min（t，n），令 E（n）=subs（t=/2-1，ln_max（t，n）），F（n）=subs（t=/2-1，ln_min（t，n）），則 E（n）＞ln（/2）＞F（n）.

令h2（n）=subs（ln（/2）=E（n），h1＋）＋subs（ln（/2）=F（n），h1-）；

令h3（n）=subs（=_to_ra（tn）[2]，h2（n）＋）＋subs（=_to_ra（tn）[1]，h2（n）-），則對任意n∈N，h3（n）＞h2（n）＞h1.h3（n）是含n 的有理式且容易得到h3（5）＜0，所以h1＜0，從而f2（/2）＜0.

f2（/2）＜0 就得到f4（/2）＜0 成立.又由引理2.1 知f2（/3）＞0，所以f4（/3）＞0，從而在（/3，/2）內存在唯一x0使得f4（x0）=0，并且在（/3，x0）內f4（x）＞0，從而f2（x）＞0，在（x0，/2）內f4（x）＜0，從而f2（x）＜0.

而f2（x）=f1（`x），所以f1（x）在（/3，x0）內單調上升，在（x0/2）內單調下降.由推論2.1 知f1（/3）＞0，從而f1（x）＞0 在（/3，x0]內成立；而f1（/2）=0，所以f1（x）＞0 在（x0/2）內成立.所以f1（x）＞0 在（/3，/2）內成立.

由推論2.1 和引理2.3 知f1（x）＞0 在（0，/2）內成立，從而 （fx）＞0 在（0，/2）內成立，即定理2 成立.

3 結束語

逐次Taylor 替換是處理超越函數多項式不等式自動證明的有效方案，其主要思路是借助Taylor 展開式建立一個逼近目標函數的多項式套，從而將證明轉化為一系列的一元多項式不等式的驗證，然后借助BOTTEMA 等代數不等式證明工具完成最后的工作.算法可以處理含多個不同超越因子和復合超越因子的超越函數多項式不等式，在證明過程中若結合人工證明和巧妙的代換方法，更能發揮逐次Taylor 替換算法的效能.

本文解決了一個一類形如sin（x）/x＞u（x）v(x)的冪指函數不等式的機器證明問題，是逐次Taylor 替換成功運用的案例.雖然結論是已知結果，但方法本身對同類不等式具有示范性，能夠為文獻[1-11]中其它冪指函數不等式（或冪函數不等式）的機器提供證明方案.