形式三角矩陣環上(F,F)-Gorenstein投射模
何東林,李煜彥
(隴南師范高等專科學校數信學院,甘肅 隴南 742500)
Gorenstein 同調理論是相對同調代數的重要內容.1969年Auslander 和Bridger[1]討論了雙邊Noether 環上有限生成模的G-維數,1995年Enochs 和Jenda[2]給出任意環上Gorenstein 投射模的概念,由于Gorenstein 投射模有許多與投射模類似的性質,引起了很多作者的關注和研究.特別地,Pan 等人[3]將其推廣到(X,Y)-Gorenstein 投射模.易知(P,P)-Gorenstein 投射模就是Gorenstein 投射模,其中P 表示投射模類.形式三角矩陣環作為環論中一類重要的非交換環,在環模理論和代數表示論中扮演著重要的角色.2011年Enochs 等[4]研究了形式三角矩陣環上的平坦覆蓋與極小Quillen 分解.2014年Eshraghi等[5]進一步討論了形式三角矩陣環上Gorenstein 投射模.自然而然地,可考慮形式三角矩陣環上的(F,F)-Gorenstein 投射模的性質和等價刻畫,其中F 表示平坦模類.
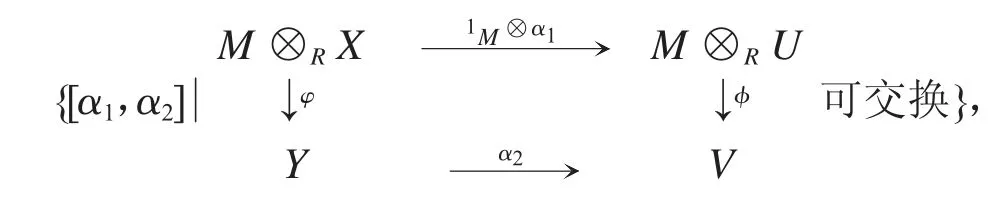
其中α1:X→U 左R-模同態,α2:Y→V 為左S-模同態.為了方便,文中的左Γ-模均用三元組的形式.對應地,左 Γ-模同態均用二元組[α1,α2]的形式.同態[α1,α2]作用于元素均為右側作用,即同態的合成為右側合成,即對任意同態[α1,α2]與[β1,β2]的合成記為左 Γ-模中的零模簡記為0,其余未涉及的概念和記號參見文獻[7-8].
1 定義和引理
定義1[3]設A 為任意結合環,X 和 Y 均為左 A-模類且P?X.稱RM 模是(X,Y)-Gorenstein 投射模,如果存在正合列
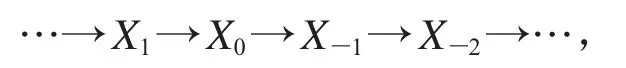
其中Xi∈X,M?Ker(X-1→X-2)且對任意Y∈Y,該序列在函子HomR(-,Y)下正合.
(1)δ 在函子HomR(-,Y)下正合;
(2)對所有i∈Z,短正合列0→Kerfi→Xi→Kerfi-1→0 在函子HomR(-,Y)下正合.
證明 由Hom 函子的性質易證.
引理2[4]是左Γ-模,則以下條件等價:
(2)φ :M?RX →Y 是單同態,X 是平坦左 R-模且余核 Cokerφ 是平坦左 S-模.
(1)Ker([α1,α2])=其中(對任意m∈M,x∈Kerα1).進而[α1,α2]是單同態當且僅當 α1,α2均為單同態.
(2)Im([α1,α2])=其中u∈Imα1).進而[α1,α2]是滿同態當且僅當 α1,α2均為滿同態.
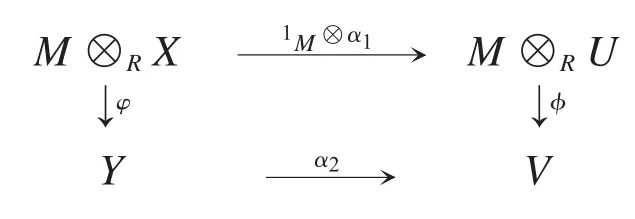
即(1M?α1)φ=φα2.因為對任意 m∈M,x∈Kerα1,有
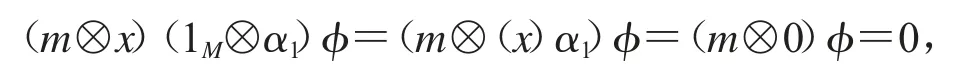
可見(m?x)φα2=0,(m?x)φ=Kerα2.不妨令
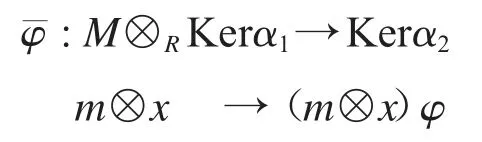
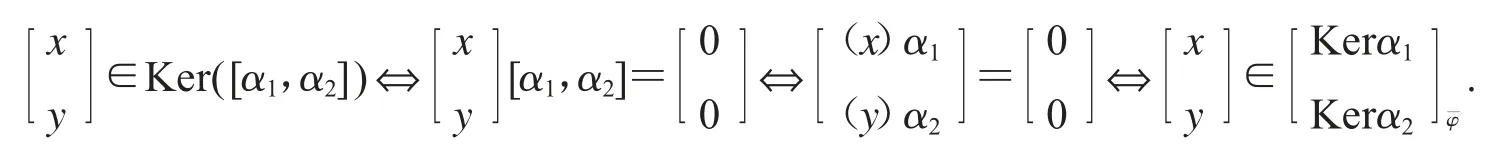
注意到下圖可交換
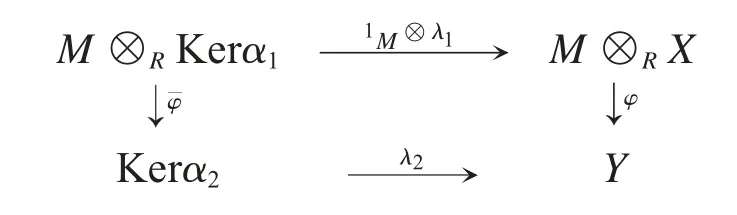
(2)證明過程與(1)對偶.
為了方便,下文中均假設ε 是左Γ-模復形,ε 及與其相關的導出復形具體形式如下:
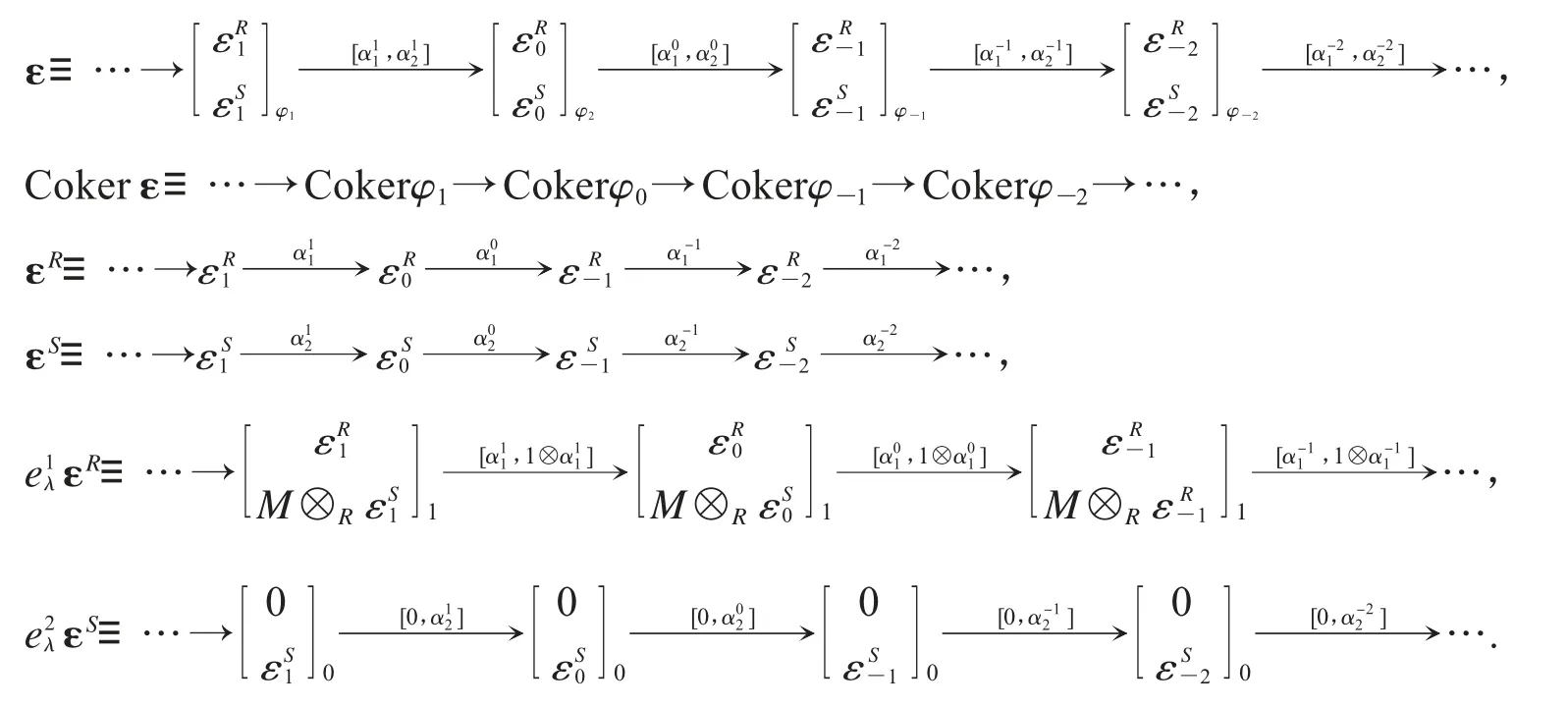
引理4 復形ε 為正合復形當且僅當εR和εS均為正合復形.
2 主要結論
定理1 設εR為正合復形,且εR在M?R-下仍正合.則以下條件等價:
(1)對任意FR∈RF,εR在函子HomR(-,FR)下仍正合;
(2)對任意FR∈RF 和i∈Z,正合列下正合;
證明由εR為正合復形且εR在M?R-下正合易知,導出復形也是正合復形.根據引理 1 和引理 3 可得(1)?(2)且(3)?(4).只須證明(2)?(3).
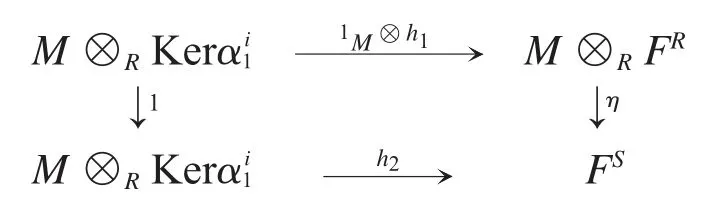
可交換,即(1M?h1)η=h2,所以
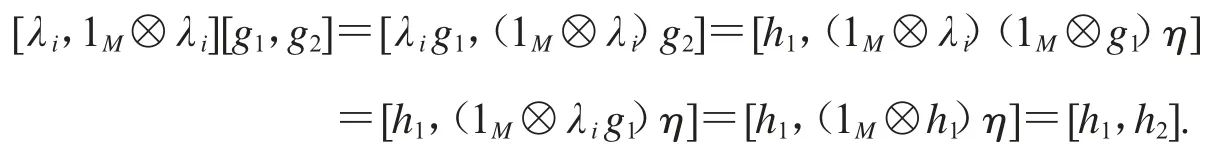
(3)?(2)對任意 FR∈RF 和 i∈Z,由引理 2 知是左Γ-平坦模.對任意模同態考慮左Γ-模同態由(3)知存在同態使得
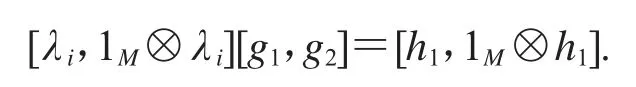
定理2 設εS為正合復形,且 M?RF?SF⊥.則以下條件等價:
(1)對任意FS∈SF,εS在函子HomR(-,FR)下仍正合;
(2)對任意FS∈SF 和i∈Z,短正合列在HomS(-,FS)下正合;
證明 由εS為正合復形易知,導出復形是正合復形.由引理1 和引理3 得(1)?(2)且(3)?(4).只須證明(2)?(3).
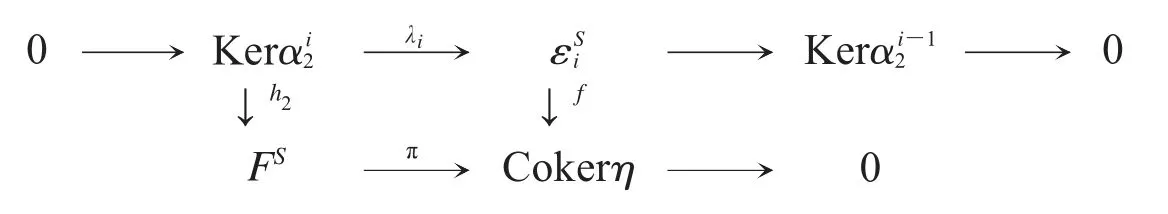
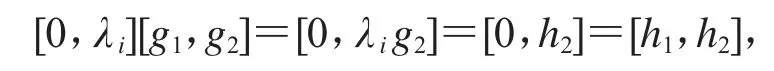
[g1,g2]就是滿足要求的同態.因此正合列在函子HomR(-,F)下仍正合.
(3)?(2)對任意 FS∈SF 和 i∈Z,由引理 2 知是左Γ-平坦模.要證短正合列在函子 HomS(-,FS)下仍正合,只須證對任意左 S-模同態總存在同態使得注意到為左Γ-模同態,由(3)知存在同態使得可見不妨令則 g 就是滿足要求的同態.因此在HomS(-,FS)下正合.
(2)對任意QR∈RF 和QS∈SF,有εR在函子HomR(-,QR)下正合且Coker ε 在HomS(-,QS)下正合.
證明 由ε 為正合復形和引理4 易知,εR和εS為正合復形.又由εR在M?R-下正合知,M?RεR也是正合復形.因為由引理 2 可知且 φi為單同態.根據復形正合列 0→M?RεR→εS→Coker ε→0 得,Coker ε 也是正合復形.考慮復形短正合列
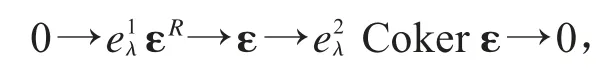
由定理3 易得如下結論.
推論2 設εR和εS均為正合復形,下正合且M ?RF?SF⊥.則以下說法成立:
(1)如果 U 是(F,F)-Gorenstein 投射左 R-模,那么是(F,F)-Gorenstein 投射左Γ-模.
(2)如果 V 是(F,F)-Gorenstein 投射左 S-模,那么是(F,F)-Gorenstein 投射左 Γ-模.
定理4 設εR和εS均為正合復形,下正合且則以下條件等價:
(2)X 是(F,F)-Gorenstein 投射左 R-模,Cokerφ 是(F,F)-Gorenstein 投射左 S-模且 φ是單同態.
3 總結
利用同調代數的方法,研究了形式三角矩陣環Γ 上的(F,F)-Gorenstein 投射模.結果表明由模RX 和SY 以及左S-同態φ:M?RX→Y 組成的Γ-模是(F,F)-Gorenstein 投射模,當且僅當RX 和SCokerφ 均是(F,F)-Gorenstein 投射模且 φ 為單同態.從而補充了形式三角矩陣環上模的基礎理論.

