析錯因思策略獲方法
摘? ? 要:講評試卷是數學教學中必不可少的常規環節,是反饋與調控學生知識技能、思想方法和掌握情況的重要手段,但當前小學畢業階段的試卷講評還存在“高投入低效益”的問題。基于此,本文通過“把脈”學生答題錯因,從結果與過程這兩個方面來談試卷分析對策,以應對此階段數學題綜合性強的問題。
關鍵詞:畢業試題;分析與講評;分析對策
中圖分類號:G427? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼:A? ? ? ? ? ? ? ? ? ?文章編號:2095-624X(2019)25-0090-02
引? ? 言
隨著評價方式的轉變,小學數學畢業階段考查重心已由原來的偏重知識技能熟練程度的靜態檢測,轉向了關注知識形成、操作驗證、信息汲取等能力的動態檢測。這種轉變對學生在思考問題的深度和溝通知識點之間內在聯系方面的觀察、分析、切換信息能力都提出了新的要求[1]。然而,教學中的習題資料卻未發生相應的轉變,這導致學生在解決問題時錯誤百出,甚至無從下手。如何化解這一矛盾,提質保效呢? 筆者認為,教師可以從以下幾方面做起。
一、結果與過程并重,以過程性突破“思維提升”
在試卷分析中教師如果就題論題,只關注學生答題的結果,不關注學生的思考過程,會造成教學上過多地關注用公式或規律解決問題,忽視公式和規律形成過程這一現象,而這恰恰是知識最本質、最核心的部分。應對過程性錯誤,教師可分三步展開。
1.追蹤思維痕跡,“把脈”錯誤成因
對于過程性問題的檢測,學生并不是完全不會解答。
錯題呈現:圓的半徑是4厘米,它的面積是(? ? )平方厘米;如果把圓平均分成若干份,剪拼成一個近似的長方形,這個近似的長方形的長是(? ? ?)厘米。
錯誤解法:2×4=8(cm)(人數較多)
錯因分析:已知圓的半徑,能求其周長和面積,但學生在學習圓的面積公式時沒有完全明白圓轉化成近似長方形后,它們之間有什么聯系。所以,學生在解決第二個問題時,把“近似的長方形”的長算成是直徑了。
從學生的錯因分析中我們發現,學生的思維障礙就是在最抽象的一環,“圓周長的一半”怎么就等于近似長方形的長了?因此,安排學生自查分析錯因,更能讓教師準確“把脈”,進而針對性完善。
2.追尋問題本質,促進問題解決
教師應以學生自我分析為前提,再現知識的形成過程,促學生知其然,更能知其所以然。
錯題呈現:根據6×4、6×4÷2,把圖畫完整(見圖1)。
錯誤解法:沒畫或畫錯。
學生錯因分析:一類學生表示沒看懂題意,不知道怎樣把算式與圖形聯系起來。
另一類學生表示看到“6×4”想到的是長方形的“長與寬”,所以把圖形補成了長方形。
檢測后發現:根據“6×4”畫出“平行四邊形”的占43%,畫出“長方形”(見圖2)的占38%,將近19%的學生有拼、有補,答錯了。從此題發現:在平時練習時,學生已經習慣了已知底和高求面積,形成了一定的思維定式。因此,筆者以錯題為媒介再次讓學生經歷知識形成的過程,從而實現自主構建。
3.整理歸納要點,提升思維深度
錯題講解分析后,及時跟進對知識點的整合和歸納,這是避免學生再次出錯的重要步驟。教師可以引導學生采用“語言描述”的方法做一份“自我整理”,這不僅能幫助學生整理與小結解決問題的要點,而且是實現知識內化、思維提升的重要一環。
二、提取與切換合理應用,以分層操作突破“綜合性強”
信息量大、綜合性強是試卷命題發展的必然趨勢。豐富、多元、綜合的信息,可以培養學生分析、提取、整合信息的能力,但是也會造成學生審題時出現無法汲取有用信息的問題。
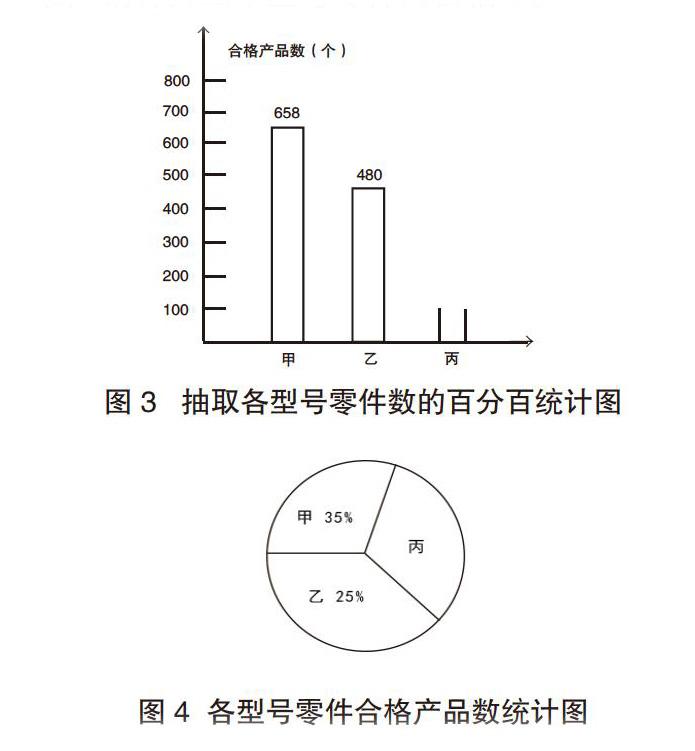
例題:質檢部門對甲、乙、丙三種型號的零件及合格產品抽檢,隨機共抽取了2000個零件,抽到的每種型號零件數量不同。抽檢結果顯示,丙型號零件合格率為95%。下面是根據質檢結果繪制的兩幅不完整的統計圖(見圖3、圖4)。
(1)參見抽檢的丙型號零件有多少個?(2)計算出丙型號零件合格產品個數,并在條形統計圖中補充完整。(3)請計算出甲型號零件的合格率。
題中出現了“抽樣總數”“抽樣百分率”“合格數量”和“合格百分率”等大量信息,而且有些信息就蘊含在圖形中,這給學生理解題意、分析信息增加了難度。一道簡單的有關百分率的問題,如單獨設計,解題正確率不會低于80%,但是置身于這種問題情境中,學生的正確率降至60%左右。可見,引導學生學會耐心細致、逐條分析信息,汲取問題解決的必要信息,從而正確解題問題,是講評練習卷時不可忽視的關鍵點。
1.分析信息—逐條分析,讀懂題意
當信息呈現量多、面廣、形式多樣的情況時,教師在講評試卷前必須引導學生對信息做梳理與分析。如例題,教師首先可以聯系實際分析問題,其次分析“隨機共抽取了2000個零件”指的是什么?從“扇形統計圖”和“條形統計圖”中能得到什么信息等。這是學生正確解題的前提。
2.提取信息—利用標注,明確思路
這類習題另一特點就是隱藏了部分信息,這就需要用標注的方式把不完整的信息清晰地呈現出來。
對于例題中的 (1)(2):出現“2000×95%”或“(2000-856-280)×95%”兩種錯誤。
教師錯因診斷:從檢測情況看,問題(1),正確率相對高些,原因在于提取有用信息簡單,而問題(2),對準確分析信息、提取信息的要求高些,求的是問題(1)的結果的95%是多少?錯誤率較高。從學生答題情況看,主要是受多余信息的干擾,不能準確提取有用信息。
分析講解這類題時,教師必須引導學生根據問題尋找、提取必要信息,并在問題旁進行適當的標注,同時也可以記錄解題的思路,幫助學生建立解決問題的方法。
3.切換信息—溝通聯系,靈活轉換
基于豐富的數學信息,教師可以借助題目要求學生深入思考,如“你還能從這些信息中聯想到哪些新的數學信息嗎”“你還能根據這些信息提出其他的數學問題嗎”等,從而實現知識點的切換、思維的發散。
當學生提出“想知道哪種零件抽檢數量最多?”這個問題時,教師可以通過“甲∶乙∶丙=35%∶25%∶40%=7∶5∶8”,實現統計、百分數、比信息間的轉換。當學生提出“如何知道哪種零件抽檢的情況最好,對這個部門進行獎勵?”這個問題時,教師就能充分挖掘統計的意義,引導學生用百分數解決統計中的決策問題等。教師只有給學生提供充足的時間、合理的思考方式,才能充分挖掘這類習題的價值,真正溝通知識間的聯系,實現信息間的切換。
結? ?語
綜上所述,策略作為解決問題的一種計策,需要學生在解決問題的過程中不斷體驗,自主反思,也需要教師的引導與概括。因此,教師只有讓策略在自然、和諧的氛圍中自由呼吸、自我成長,才能促進學生有意義地生成策略,引發學生自主用策略與方法解決問題,從而真正實現數學教學的高質、高效。
[參考文獻]
蔡水華.借幾何直觀 促問題解決[J].教學月刊小學版(數學),2012(10):43-45.
作者簡介:王嬋丹(1979.1—),女,浙江奉化人,本科學歷,一級教師。

