基于GARCH效應和改進罰指標的時域非線性損傷識別

郭惠勇， 黃 淇

(重慶大學 土木工程學院； 山地城鎮建設與新技術教育部重點實驗室，重慶 400045)

近年來，基于時間序列模型進行損傷識別研究的方法得到了國內外學者的廣泛關注[1].基于時間序列的損傷識別方法可以直接利用結構的加速度響應等時程數據，對其進行統計分析并建立相關的時序模型，并進行損傷的識別和判定.目前，采用線性時間序列模型進行損傷識別的研究較多[2-3]，廣泛采用了自回歸(AR)、有源自回歸(ARX)、自回歸滑動平均(ARMA)、有源自回歸滑動平均(ARMAX)等線性模型進行損傷識別研究，并取得較好的成果.Fassois等[4]對基于時間序列的損傷識別方法進行了初步綜合研究，并結合實驗驗證了這些方法的實用性和有效性.Zheng等[5]將ARMA模型和倒譜距離相結合，對一個層間剪切模型進行了識別研究.模擬測試結果顯示了倒譜距離指標的高效性以及白化濾波技術對識別結果具有改良作用.Silva等[6]則基于ARX模型對結構進行了損傷識別研究，其利用了殘差和主成分分析對美國土木工程協會(ASCE)的基準結構進行了損傷識別驗證.Nair等[7]則采用了ARMA模型對結構振動數據進行了數據擬合，利用了AR部分的前3階系數函數構造損傷指標，同樣也利用ASCE的基準結構進行了損傷定位分析.Saaed等[8]則利用了線性ARMAX模型進行了鋼框架的損傷檢測研究.羅德河等[9]則基于ARMAX模型計算了系統的脈沖傳遞函數，利用脈沖響應系數建立了損傷指標，并對混凝土壩進行了損傷診斷研究.

在實際工程中，結構的損傷往往具有非線性特性，例如損傷裂紋在結構時程荷載作用下會產生張開和閉合效應，這樣采集的響應常具備時程非線性特征，如采用線性模型則難以精確描述非線性損傷狀況，只能給出近似的結果.為了更為準確地提取時間序列中的非線性損傷信息，有必要采用非線性模型.Bollerslev[10]提出了一種廣義自回歸條件異方差(GARCH)模型，該模型是一種較好的非線性模型，最早應用于金融領域時間序列波動率的研究，現在已逐步應用于其他領域[11-13].Chen等[13]利用了ARMA/GARCH組合模型進行了結構健康監測研究，并構建了一種損傷敏感特征算法進行損傷識別.但是，該類算法只是對自由度數據信息進行建模，并不能直接有效反映單元剛度損傷狀況，需要利用剛度指標進行損傷轉換，故本文提出了一種基于GARCH模型的罰函數剛度轉換指標.

1 非線性信號的GARCH建模方法

1.1 GARCH模型基本原理

GARCH模型是一種時間序列波動率的預測方法，可以用過去時間的方差和誤差信息來預測當前時刻的波動率方差.由于GARCH模型對于方差時變的時間序列信號具有較好的預測功能，該模型已經應用于股票預測、匯率估計以及目標探測等領域[14]，并取得了較好的預測結果.基于時間序列預測的GARCH模型原理如下.

對于一個離散的時間序列數據集{yt}，t-1時刻可以利用的已知信息為ψt-1，就可以利用該已知信息得到在t時刻預測值，記為yt|ψt-1.這時，在t時刻條件預測誤差εt可以表示為

εt=yt-E[yt|ψt-1]

(1)

式中：t∈[1,N]，N為時間序列數據總的時刻數.則在t時刻時間序列數據的條件方差vt可以表示為

(2)

可以利用過去I個時刻的條件方差和J個時刻的條件預測誤差構建當前條件方差vt的函數關系：

(3)

這樣，就定義了一個GARCH(I,J)模型.GARCH(I,J)模型可以表示為

vt=ζ0+ζ1vt-1+ζ2vt-2+…+

(4)

式中：ζ0、ζi(i=1,2,…,I)和ηj(j=1,2,…,J)均為GARCH模型的參數，并且滿足

ζ0>0,ζi≥0,ηj≥0

1.2 非線性信號的GARCH建模

結構構件發生裂紋等損傷后，在時程荷載作用下會產生時程響應數據集{yt}.由于裂紋的張開和閉合效應，張開時剛度降低，閉合時剛度恢復，這時候的時程響應會包含非平穩的非線性信號和平穩的線性信號.為了有效提取該非線性信號，為后續的非線性損傷識別建立基礎，需要對時程非線性信號進行有效的提取和建模，并需要過濾掉時程響應中包含的線性信息.可以通過線性模型(如AR模型)來過濾時程響應中的線性信息，保留待識別的非線性誤差信息，具體為

(5)

式中：δ為AR模型的一個常量；p為模型自回歸的階數；φi為模型自回歸系數.通過測量信號和自回歸模型可以計算非平穩誤差信息，再通過下式可以獲取條件方差vt：

(6)

式中：zt為均值為0、方差為1的白噪聲序列.利用條件方差和條件誤差項可以建立GARCH(I,J)模型：

(7)

1.3 參數估計和模型定階

由于GARCH(I,J)模型的參數估計比較復雜，在實際的應用當中通常用其簡化的一些形式，例如GARCH(1,1)模型或者GARCH(0,J)模型.其中GARCH(1,1)模型階數已經確定，所以主要分析GARCH(0,J)模型的參數估計.可采用極大似然函數估計模型參數，建立GARCH(0,J)似然函數：

f(ε1,ε2,…,εN|θ)=

(8)

式中：θ為未知估計參數.略掉邊際分布，可得條件似然函數為

f(ε1,ε2,…,εN|ε1,ε2,…,εJ,θ)=

(9)

則對數條件似然函數為

lnL(θ)=

(10)

對于極大似然估計，上式第1項不含參數，可忽略，故上式修改為

(11)

由于GARCH模型是建立在自回歸模型提取的殘差序列{εt}的基礎上，需檢驗殘差序列的GARCH效應，并確定GARCH模型的階數.具體可以使用赤池信息準則(AIC)或貝葉斯信息準則(BIC)進行GARCH模型的定階.采用AIC可以表示為

AIC=-2lnL+2m

(12)

式中：lnL和m分別為最大似然函數和估計參數數量.AIC之所以能夠用來確定一個模型的階數，是因為一個最優的模型階數總能產生一個最小的AIC值.在實際應用中，應該盡量選取較小的階數以簡化計算.

2 基于GARCH效應的損傷識別及其改進罰指標

2.1 時域非線性剛度分析

在實際工程中，結構出現的損傷往往具有非線性特性，例如桿件裂紋、節點螺栓脫落等損傷.在時程荷載作用下會產生張開和閉合效應，當裂紋張開時，構件的剛度會降低為裂紋處凈截面對應的剛度，當裂紋閉合時，其剛度恢復為原始剛度，這時的結構響應就會具有時域非線性特性，其剛度也具有雙線性剛度特征.因此，雙線性剛度方法可以用來模擬結構的時域非線性損傷，該方法可以較為準確地描述結構構件在荷載作用下裂紋的張開閉合效應引起的剛度變化，并保證了裂紋張開時的側向剛度比裂紋閉合時的剛度小，具體為

ki(xi(t))=

(13)

式中：xi(t)(i=1,2,…,n)和xi-1(t)(i≠1)分別為第i層和第i-1層的t時刻的側移，當i=1時,xi-1(t)=x0(t)=0，x0(t)為結構基礎的側移；ki(xi(t))表示第i層的層間剛度；α為結構的非線性損傷系數，如果α=0，剛度是未折減的，也就意味著系統未損傷，如果α=1，意味著模擬非線性損傷源的構件完全破壞.通過對非線性損傷的剛度分析，可知其對應的時程響應往往是非平穩的，需要采用GARCH等模型從時程響應中提取相應的非線性特征.

2.2 基于GARCH的損傷識別及基本剛度損傷指標

通過對非線性損傷時程響應進行GARCH建模，以提取非線性損傷產生的非平穩信息，并與無損狀態下的時程響應非平穩信息進行對比，以消減環境等不確定因素的干擾，從而可以提取非線性損傷信息并進行識別.其基本損傷識別步驟如下：

(1) 獲取基本狀態和損傷狀態下的加速度響應，然后進行差分滿足數據平穩性要求，利用式(5)消減線性影響，獲取相應的殘差數據并檢驗GARCH效應.

(3) 利用無損狀態和損傷狀態下的各個樓層的歸一化差值，構建剛度損傷指標，并進行結構非線性損傷識別.其中構建基本剛度損傷指標的方法為：由于傳感器測量的響應數據主要是樓層處的響應，該位置反映了該處自由度的數據變化.當從一個具有非線性損傷的n層層間剪切結構上采集加速度響應時間序列，線性AR模型就不能夠完全擬合該時間序列.利用消減線性方法可以提取出殘差序列{εt}，該序列條件異方差序列{vt}不再是常量，會隨著時間上下波動.因此，條件異方差序列{vt}的方差s(vt)將是一個非0值，所以可以利用該值進行非線性識別.則基于第j層自由度的概率化條件方差變化為

(14)

由于層間剛度與自由度不具有一一對應關系，采用基于自由度的方法難以直接觀測出層間非線性剛度損傷，則可采用基本GARCH剛度損傷指標(簡稱為基本GARCH指標)：

(15)

可令Q0=0，這樣上式完全滿足概率化要求，可進行基于層間剛度的損傷識別.

2.3 改進GARCH罰指標

由于基本GARCH指標只是簡單利用了相鄰自由度的信息，其仍難以準確判斷損傷位置，所以，本文借鑒罰函數原理提出了一種改進的GARCH剛度損傷指標，以進一步提高損傷識別的準確性.考慮基本GARCH指標主要因相鄰的不相關因素而對損傷位置識別產生干擾，故借鑒罰函數原理對損傷識別指標進行改進，改進后的剛度損傷罰指標(簡稱為改進GARCH罰指標)可表示為

(16)

(17)

式中：γ為懲罰參數，該指標利用懲罰項來消減相鄰的不相關因素對損傷位置判定的干擾.

3 數值計算

考慮如圖1所示的8自由度層間剪切結構，其中每層的質量均為100 kg，層間剛度為1 MN/m，采用的瑞利阻尼參數分別為 0.984 2 和0，罰參數為0.4.該結構的非線性損傷采用式(13)的雙線性剛度來模擬，這樣可以通過一個簡化的方式來模擬相鄰樓層間的柱子在荷載作用下，水平裂紋的張開閉合引起的剛度變化，從而使裂紋張開時的剛度比裂紋閉合時的剛度小.為了充分評價GARCH模型和損傷指標的有效性，考慮了該8層結構每層剛度k依次發生損傷的情況，每層均考慮了損傷程度20%和30%的折減，這樣共有16種工況.利用白噪聲數據作為基礎激勵數據，運用Wilson-θ算法可得出該8層建筑結構的每層的加速度響應時間序列，其中計算步長為0.05 s.

圖1 8層剪切結構Fig.1 Eight-storey shear structure

為了確保與實際工程的一致性，根據經驗，每條加速度響應時間序列都會加入5%的測量噪聲.本文采用通過巴特沃斯低通濾波器處理的隨機白噪聲序列來模擬結構響應加速度的測量噪聲，將白噪聲序列振幅調整到加速度響應值同一水平，再乘以設定的測量噪聲水平值得到模擬的測量噪聲.將該調整后的測量噪聲與原始加速度響應時間序列相加即可得到含有測量噪聲的加速度時間序列：

(18)

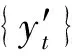
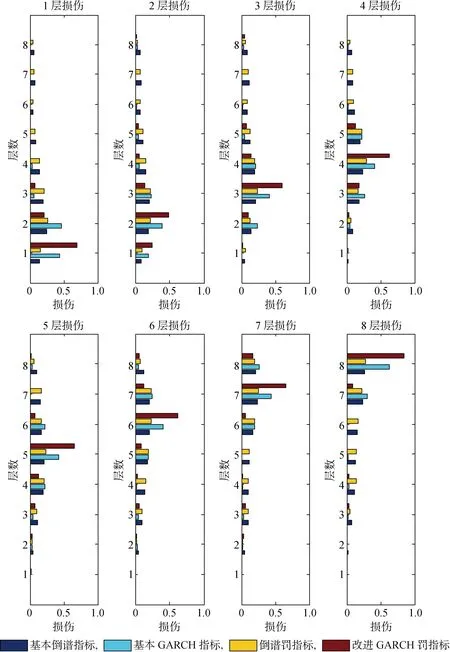
圖2 1～8層在20%損傷下的識別結果Fig.2 The damage detection results for 1st-storey to 8th-storey with 20% damage degree

采用簡化的GARCH(0,J)進行計算，利用AIC進行定階，通過定階計算選取了J的階數為5，經檢驗可知該階數適合于該GARCH模型，并采用最大似然估計法進行了參數估計，這樣可基于該模型和相應剛度指標進行損傷識別.為了進行對比，本文也采用了Xing等[15]提出的基于AR模型和倒譜測距指標的損傷識別方法，并利用與本文類似方法將其自由度指標轉化兩種剛度指標，即基本倒譜指標和倒譜罰指標.由于損傷前后的時程響應不同，故可以通過損傷前后的時域信號構建AR模型，并采用倒譜分析計算損傷前后模型的倒譜測距，倒譜測距可以反映損傷引起的改變，在倒譜測距的基礎上仿照式(15)和(16)構建相應的基本倒譜指標和倒譜罰指標.基本GARCH指標和改進GARCH罰指標主要是利用非線性信號引起的條件方差變化來進行識別，并利用概率化條件方差變化構建相應的基本GARCH指標和改進GARCH罰指標.

首先，依次考慮第1層至第8層分別有20%非線性損傷，該8個工況的計算結果如圖2所示.圖中縱坐標為剪切結構的層數，共有8層；橫坐標為損傷度，區間為[0,1]，0表示無損傷，1表示完全損傷.由圖2可見，基于非線性GARCH模型的基本GARCH指標和改進GARCH罰指標的識別效果相對更好，基于線性AR模型和倒譜測距的基本倒譜指標和倒譜罰指標的識別結果欠佳.這主要由于時程響應中包含了非線性信息，則基于非線性模型的損傷指標識別效果相對會更好.另外，改進GARCH罰指標的識別結果要好于基本GARCH指標，例如基本GARCH指標對于第1層損傷時的計算結果會出現一些偏差，而改進GARCH罰指標的計算結果更好，因為該指標削弱了相鄰的不相關因素對損傷位置判定的干擾.

然后，依次考慮第1層至第8層分別有30%非線性損傷，該8個工況的計算結果如圖3所示.由圖3可見，基于非線性GARCH模型的兩個指標依然好于基于線性AR模型的兩個倒譜指標，這依然是由于時程響應中包含了非線性信息，則基于非線性模型的損傷指標識別效果相對會更好.另外，改進GARCH罰指標的識別結果仍要好于基本GARCH指標，這主要是由于改進GARCH罰指標削弱了相鄰的不相關因素對損傷位置判定的干擾.由于裂紋的張開和閉合效應會使桿件的剛度產生突變，從而使時程響應信號產生非線性的變化，識別結果主要是提取出這種非線性的信息，來判斷非線性損傷的位置.

4 實驗研究

采用3層框架進行非線性損傷實驗研究，具體結構見圖4(a)，該結構是由鋁柱和鋁板通過螺栓連接而成，并將該結構安裝在單向軌道上以保證它只能在一個方向上滑動.每一層的鋁柱(17.7 cm×2.5 cm×0.6 cm)和柱頂、柱腳的鋁板(30.5 cm×30.5 cm×2.5 cm)共同構建了一個3自由度的系統.此外，如圖4(b)所示，在最頂層的樓板中間固定了一根懸臂柱(15.0 cm×2.5 cm×2.5 cm)，該懸臂柱和固定在下一層樓板上的緩沖器共同構成了一個非線性損傷源.當框架結構產生振動時，兩者發生相互作用，該作用效果類似于“呼吸裂紋”[16]，可有效模擬結構的非線性動力學行為.緩沖器和懸臂柱的之間的距離可以調節，用來獲取在特定激勵下不同程度的非線性損傷，該非線性損傷源也具有雙線性剛度特點.加速度傳感器安裝在每層樓板的中間位置用來記錄結構每層的加速度響應.

圖4 3層框架結構Fig.4 The three-storey frame structure

損傷的工況如表1所示.主要是通過改變懸臂柱和緩沖器之間的距離來引入不同程度的非線性損傷，隨著距離的增加，非線性程度降低.通過模型定階和檢驗，依然選取GARCH(0,5)模型，并估計出模型參數.同樣采用了基于AR模型的基本倒譜指標和倒譜罰指標進行對比研究.本實驗無損時基準結構的加速度(a)響應曲線如圖5所示，工況2的加速度響應曲線如圖6所示，圖中的采樣時間間隔為0.005 s，通過對比相應通道的波形圖輪廓，例如對比圖5和圖6的第3通道波形圖輪廓，可看出兩者波形輪廓不同.

工況1至工況3實驗模擬了非線性損傷問題，隨著間隙的增大，其非線性程度將降低，當間隙足夠大時，緩沖器和懸臂柱將脫離接觸，從而不具有時域非線性特性.工況1的非線性損傷識別結果如圖7所示，圖中橫坐標為框架結構的層數，共有3層.由圖7可見，在較強非線性情況下，基于非線性GARCH模型的兩種指標的損傷識別結果較好，基本GARCH指標和改進GARCH罰指標的損傷值均較高，而基于AR模型的基本倒譜指標和倒譜罰指標相對欠佳.另外，改進GARCH罰指標的識別效果明顯優于基本GARCH指標.

工況2的非線性損傷識別結果如圖8所示，由圖8可見，由于間隙變大，非線性減弱，基于非線性GARCH模型的兩種指標的損傷識別結果依舊較好，基本GARCH指標和改進GARCH罰指標的損傷值仍較高，但相對于倒譜指標的識別優勢已經減弱.從4種指標的綜合對比可知，改進GARCH罰指標的識別效果最好，明顯優于其他3個指標.

表1 3層框架結構的非線性損傷工況

Tab.1 The nonlinear damage cases of the three-storey frame structure

工況間隙/mm10.0520.1030.20(弱非線性)

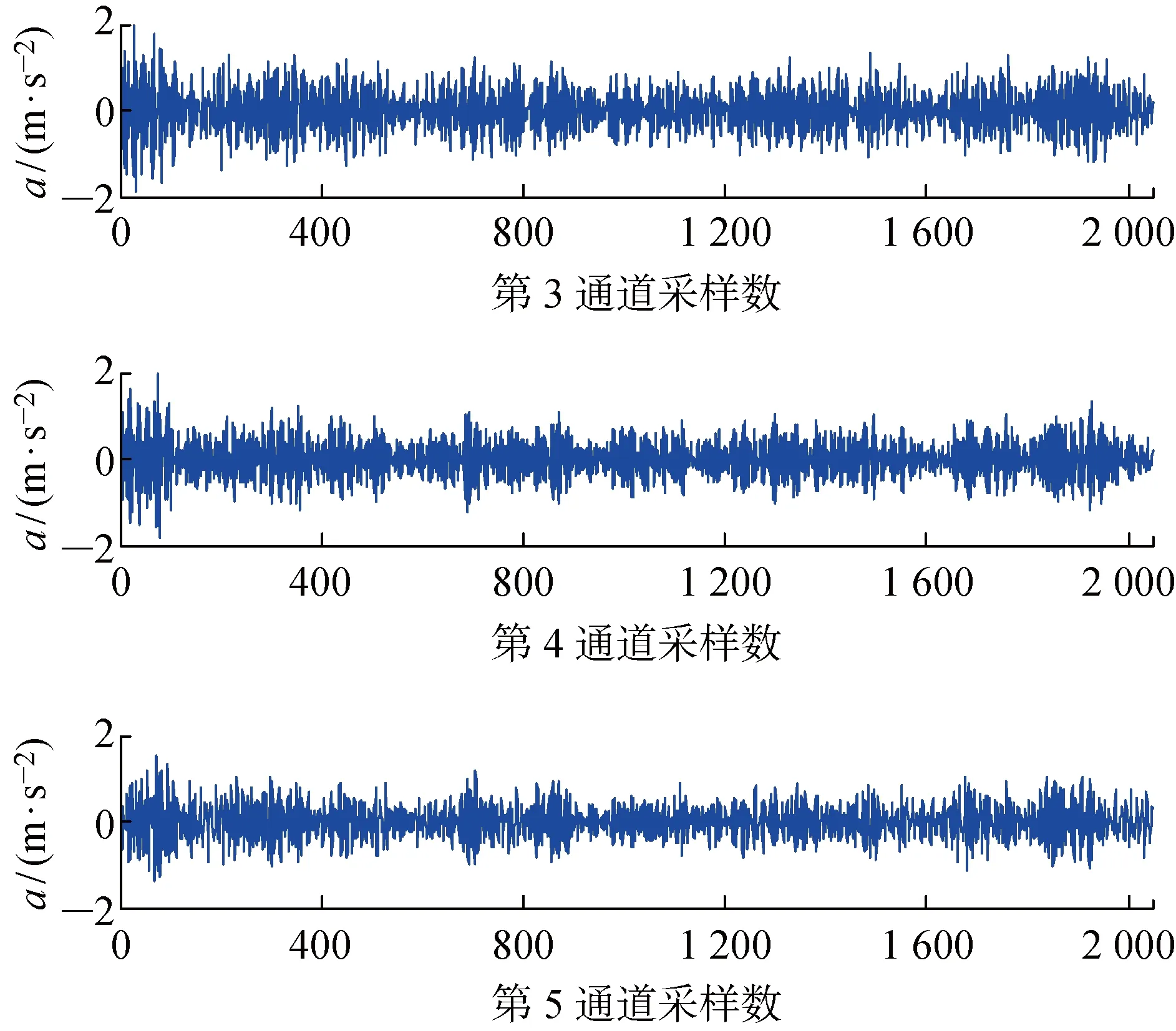
圖5 基準狀態下的加速度響應曲線Fig.5 Acceleration response time histories in basic state

圖6 工況2的加速度響應曲線Fig.6 Acceleration response time histories in Case 2

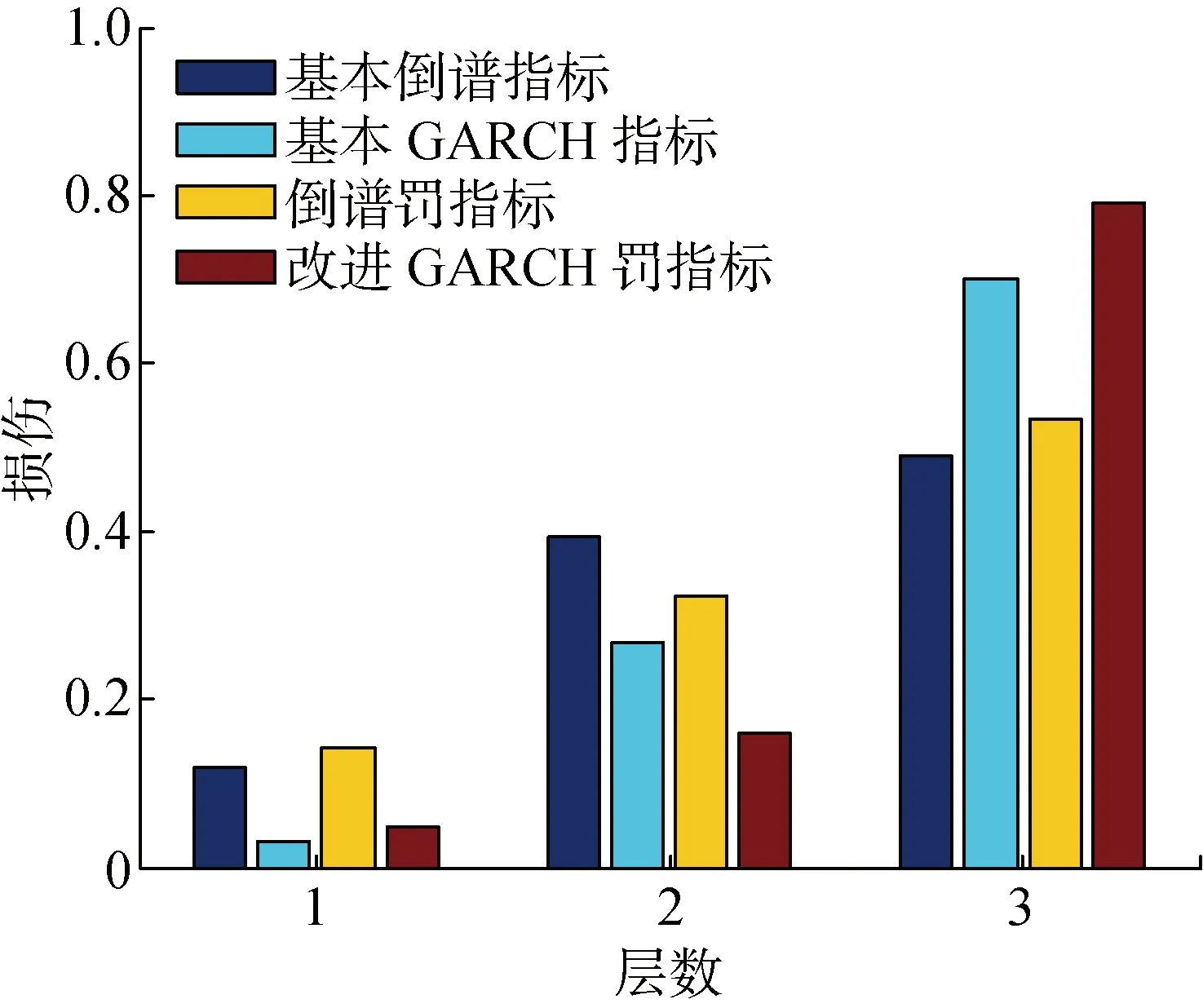
圖7 工況1的損傷識別結果對比Fig.7 The damage detection results in Case 1

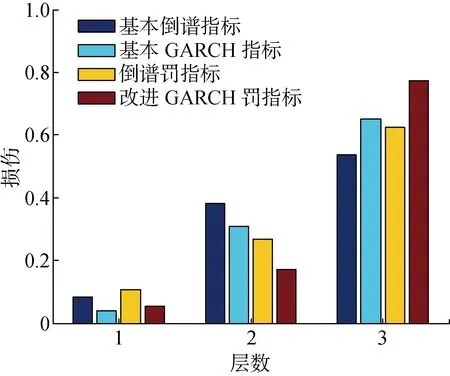
圖8 工況2的損傷識別結果對比Fig.8 The damage detection results in Case 2

工況3的非線性損傷識別結果如圖9所示，從圖9中可知，隨著間隙的進一步變大，非線性程度持續減弱，該狀態已呈現為弱非線性問題，基于非線性GARCH模型指標的損傷識別結果雖然相對較好，但相對于倒譜指標的識別優勢也進一步減弱.不過，從4種損傷指標的對比可知，改進GARCH罰指標的識別效果仍最好，仍優于其他3個指標.由3種工況可知，隨著緩沖器和懸臂柱間隙的增大，其非線性程度將明顯降低，當間隙足夠大時，緩沖器和懸臂柱將脫離接觸，從而不具有時域非線性特性.因此，工況1到工況3的非線性程度依次降低，而3種工況下第3層的改進GARCH罰指標識別結果也是依次降低，說明該指標很好地反映了緩沖器和懸臂柱間隙距離改變引起的非線性程度變化.其中，工況3可考慮為弱非線性問題，其識別結果相對于前兩個工況最差.因此，改進GARCH罰指標具有一定的非線性程度的識別能力.

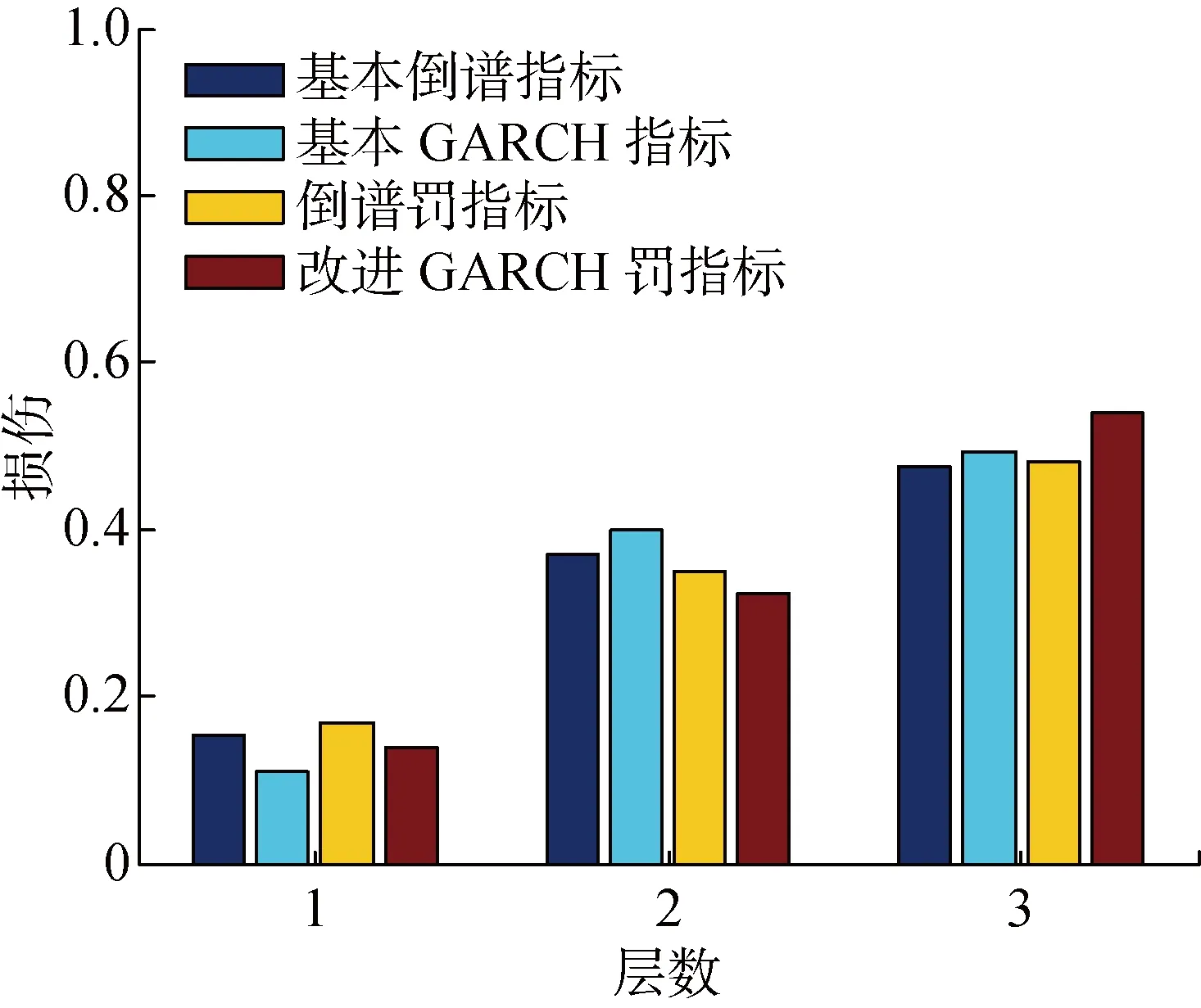
圖9 工況3的損傷識別結果對比(弱非線性狀態)Fig.9 The damage detection results in Case 3 (weak nonlinear state)

通過數值計算和實驗工況可知，對于非線性損傷問題，基于GARCH模型構建的損傷指標相對更好，這主要是由于GARCH模型屬于非線性模型，可以更好地解決非線性問題.而AR模型和倒譜測距相結合的非線性損傷識別效果相對較差，這主要是AR模型是線性模型，雖然借助了倒譜測距來增強識別效果，但該方法應該更適于解決線性損傷問題，對于環境干擾下的非線性問題識別結果欠佳.改進GARCH罰指標的識別效果相對最好，對于非線性問題，其識別結果明顯優于基本GARCH指標和基于AR模型的倒譜類損傷指標.

5 結語

本文提出了基于GARCH效應和改進罰指標的非線性損傷識別方法，該方法直接利用含噪聲的測量加速度數據，采用GARCH模型提取了非平穩的非線性損傷信號，并借助改進GARCH罰指標來識別基于層剛度的非線性損傷信息，從而實現了非線性損傷的識別研究.最后利用了數值計算和實驗研究進行了非線性損傷識別理論和改進GARCH罰指標的有效性驗證.通過實驗驗證和數值分析，可以得出以下結論：對于非線性損傷識別問題，基于非線性GARCH模型的損傷識別方法要優于基于線性AR模型和倒譜測距的方法；本文提出的改進GARCH罰指標對于非線性損傷問題的識別效果相對更好，明顯優于基本GARCH指標和基于AR模型的基本倒譜指標和倒譜罰指標；而且對于弱非線性問題，本文的改進GARCH罰指標依舊具有一定的非線性損傷識別能力.