熱載荷作用下顆粒增強復合材料溫升分布數值模擬

楊萬友， 王家序， 黃彥彥， 周青華， 楊 勇

(四川大學 空天科學與工程學院，成都 610065)

衛星、宇宙飛船等航天器常常服役于復雜空間環境中，受到高低溫、強輻射、微重力、真空等嚴酷空間環境的共同作用，材料性能被嚴重影響.尤其是寬范圍的高低溫交變，將導致材料發生熱變形和產生內部熱應力，造成材料性能退化和航天器可靠性降低.此外，針對航天器使用的高性能顆粒增強復合材料，熱量在傳遞的過程中還會受到增強體的影響，使材料表面及內部溫度場產生擾動，從而造成表面熱變形不協調、內部熱應力集中等不利后果，進一步影響航天器的可靠性[1-2].

顆粒增強復合材料作為一種典型的工程材料，其目的是通過往基體材料中添加不同材料屬性的增強體以提升基體材料性能.由于熱傳導屬性的差異，增強體的存在將會影響熱載荷作用下顆粒增強復合材料的熱平衡.對于材料熱平衡問題的理論分析方法，國內外學者開展了許多相關研究.早期的理論研究多基于均質材料這一假設，因此可用解析方法直接進行求解.如Carslaw等[3]給出了移動熱源作用下半空間表面溫升解析解.其后圓形熱源[4]、正方形和橢圓形熱源[5]作用下半空間表面溫升分布的解析公式被其他學者們推導出來.Liu等[1,6]提出了點力或者點熱源作用下求解半空間3種狀態(暫瞬態、恒瞬態和穩態)下溫升、熱應力[1]和表面熱位移[6]的頻率響應函數，這避免了采用Green函數計算溫度場時函數存在奇點的問題[7-8].

然而顆粒增強復合材料是由多種性質不同的材料復合而成，呈現出典型的非均質特性.由于其復雜的內部微觀結構，難以找到解析解求解相關的熱平衡等問題，所以，有限元法(FEM)和半解析法(SAM)等數值方法逐漸被廣大學者采用來求解非均質材料問題.如Bazyar等[9]利用比例邊界FEM求解了各向異性非均質材料的二維熱傳導問題；Mortazavi等[10]建立了有限元模型來預測各向異性隨機雙相復合材料的有效導熱系數和彈性模量，并將之與其他模型進行對比分析研究.此外，余天堂等[11]提出了以導熱系數為基本參數的熱傳導擴展FEM來研究非均質材料中的熱傳導問題；陳康等[12]給出了一種適用于梯度復合材料熱傳導分析的梯度單元法，結果表明，梯度單元和均勻單元得到的溫度場基本一致.類似研究還包括文獻[13-15].盡管FEM在各種商業軟件支持下廣泛應用于顆粒增強復合材料熱傳導分析，但是該方法具有材料微觀結構建模困難、計算耗時長、結果過度依賴網格尺寸和類型等缺點.

為了克服上述FEM的缺點，學者們提出利用SAM來求解與顆粒增強復合材料相關的科學問題.在Eshelby[16]提出等效夾雜方法(EIM)求解非均質材料彈性場這一開創性工作之后，SAM被逐漸發展、豐富和完善[17-22]，可求解含任意形狀、分布增強體顆粒增強復合材料的粗糙面彈性接觸問題.然而對于顆粒增強復合材料熱平衡分析，目前鮮有文獻報道.Hatta等[23]類比Eshelby[16]提出的彈性場等效夾雜方法，將應力對應熱流密度、應變對應溫度梯度、彈性模量對應導熱系數，提出了適用于求解含圓/球形、橢圓/球形增強體顆粒增強復合材料的穩態熱傳導全空間等效夾雜方法.然而，全空間解只能處理遠端熱載荷問題，真實熱載荷作用下顆粒增強復合材料的熱平衡問題則需要在半空間條件下求解.

本文將顆粒增強復合材料中增強體設定為橢球，利用鏡像法[24]完成熱傳導等效夾雜方法從全空間到半空間的轉換，用于研究熱載荷作用下顆粒增強復合材料內部和表面溫升分布規律.分析了不同導熱系數、深度和位置朝向的增強體對顆粒增強復合材料熱平衡行為的影響，并通過對含任意分布球形增強體顆粒增強復合材料溫升分布進行求解，驗證了算法處理真實顆粒增強復合材料熱平衡分析的能力.

1 基本理論和方程

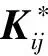
(1)

圖1 穩態熱傳導等效夾雜方法Fig.1 EIM for steady state heat conduction

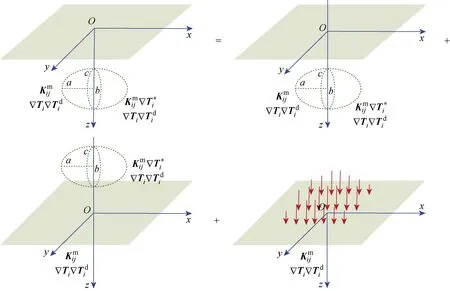
圖2 鏡像法基本原理Fig.2 Basic principle of method of images

采用鏡像法[24]，實現穩態熱傳導EIM從全空間到半空間的轉換.基于鏡像法原理(見圖2)，半空間夾雜引起的溫度梯度量是兩個全空間夾雜引起的溫度梯度量和對稱面法向熱流引起的溫度梯度量之和，其求解方法詳見文獻[1,23].

進一步引入類似彈性場中的Eshelby張量Sij，文獻[25]已給出其推導過程及具體形式，此處不再贅述.利用Eshelby張量Sij關聯擾動溫度梯度與本征溫度梯度：

(2)

將上式代入式(1)整理得

(3)

(4)

式中：Φ,i為牛頓勢函數Φ的一階導數，詳情參見文獻[25]；xi為目標溫度坐標點到增強體單元中心坐標的向量.顆粒增強復合材料總溫升Tt為均質材料溫升T與增強體擾動溫升Td之和[26]：

Tt=T+Td

(5)

(6)

式中：Sij為關聯第j個等效夾雜相應溫度梯度與第i個本征溫度梯度之間相互影響的系數；n為增強體的數目.

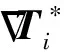
2 顆粒增強復合材料熱平衡算法驗證

利用熱載荷作用下含單橢球增強體顆粒增強復合材料模型驗證本文所提算法的有效性.模型示意圖如圖1(a)所示，其中橢球形增強體尺寸設置為a=2b=2c=r/2，并令其中心距離表面h=r.外部加載熱流密度可表示為

(7)

模型計算區域大小設置為6r×6r×3r，等距離散為128×128×64個網格點，利用上述算法對不同導熱系數(K*=4Km或K*=Km/4，其中，基體材料導熱系數Km=50.2 W/(m·K)[1])增強體進行計算.同時，利用Abaqus軟件中軸對稱方式建立同樣條件的有限元驗證模型，如圖3所示.另外值得注意的是，第1節中已直接或間接說明了本文所提模型/算法與相關的有限元分析模型基于下列3點假設：① 顆粒增強復合材料是半無限體；② 熱傳導分析是在穩態時進行；③ 顆粒增強體之間不重疊.

圖4所示為利用上述兩種方法計算得到的顆粒增強復合材料下表面溫升分布云圖，NT11表示節點溫度輸出變量.當增強體與基體導熱系數關系為K*=4Km時，增強體內部溫度等值線分布相較基體稀疏，溫度變化率較小；而K*=Km/4時，增強體內部溫度等值線分布較基體緊湊，溫度變化率較大.圖5所示為利用兩種方法計算得到的模型結果沿z軸的溫升分布.從圖5中可以看出，增強體單元對基體溫度場有一處明顯的擾動，并且K*=4Km時會在增強體距離表面近端(z/r=0.5)以及遠端(z/r=1.5)附近分別造成相對均質材料的溫度降低和升高，而增強體材料屬性為K*=Km/4時造成的影響與前者相反且相對較弱.此外，利用FEM計算的結果與本文算法模擬的結果在數值上能夠較好地吻合，驗證了所提算法的有效性.

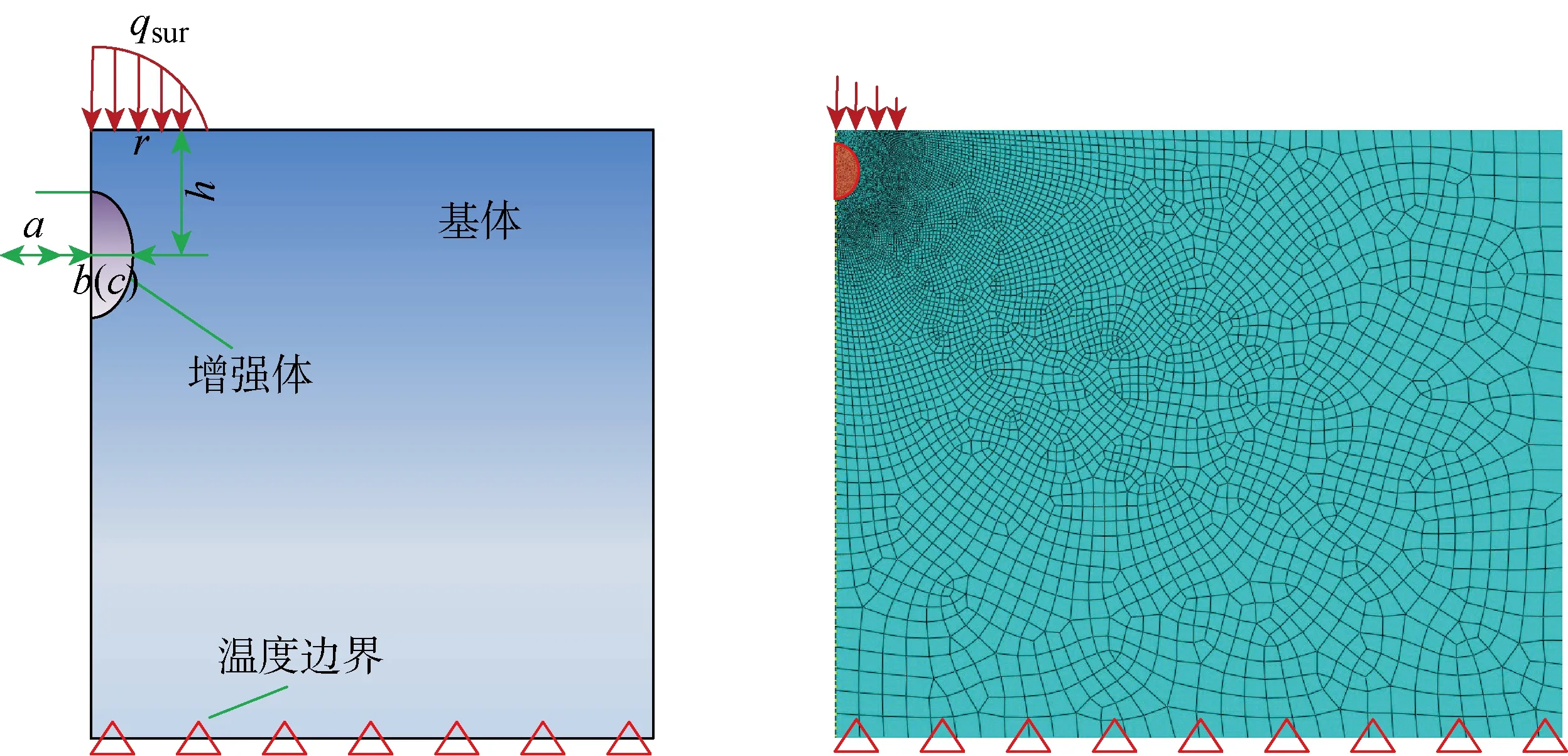
圖3 含單一橢球增強體二維有限元對稱穩態熱傳導模型Fig.3 2D axisymmetric FEM including an ellipsoidal reinforcement for steady state heat conduction

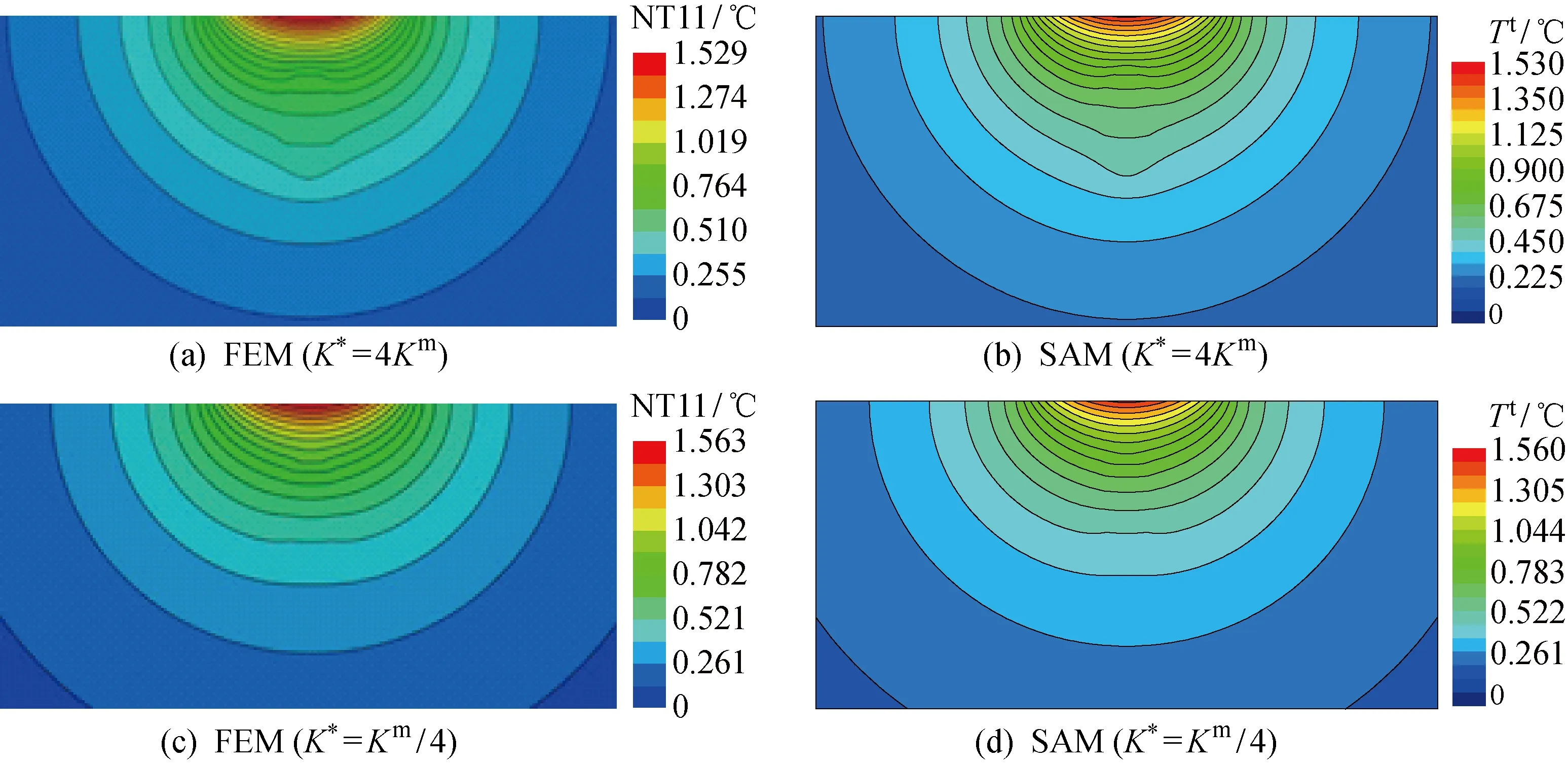
圖4 含單一橢球增強體下表面溫升分布Fig.4 Lower surface temperature rise distribution including an ellipsoidal reinforcement

圖5 含單一橢球增強體沿z軸的溫升分布Fig.5 Temperature rise distribution along the z axis including an ellipsoidal reinforcement

3 計算結果和討論

采用圖1(a)的模型，除了特別說明外，其余參數設置參見第2節，以橢球形增強體導熱系數、位置、朝向、數目為研究參數，分析其對熱載荷作用下顆粒增強復合材料溫升分布影響.

3.1 單個增強體熱平衡分析

設置橢球形增強體尺寸參數為a=1.25b=1.25c=r，增強體中心至表面的距離h=0.75r.由于橢球本身各軸長短不一，在空間中有著復雜的位置關系.如圖6所示，可采用歐拉角α、β和γ來描述橢球增強體所處的空間位置.目標點從全局坐標到局部坐標的轉換可表示為

Rxyz(m)=Rxyz(m)+

a(m,n)[Pxyz(m)-Cxyz(m)]

(8)

m,n=1,2,3

圖6 歐拉角和坐標轉換關系Fig.6 Relationship of Euler angles and coordinate transformation

式中：m,n分別代表x,y,z；Rxyz(m)和Pxyz(m)分別為目標點的局部坐標和全局坐標；Cxyz(m)為橢球中心的全局坐標;a(m,n)為對應的旋轉因子，具體可表示為

(9)

由上述歐拉角的定義，圖1(a)模型中橢球增強體各歐拉角分別為α=0°、β=90° 和γ=90°.不論增強體處于什么位置，其對溫度場或多或少都有擾動，且這種擾動直接表現為溫度的變化.本節利用表面溫度變化率η來分析各參數對材料熱平衡行為的影響.具體表達式為

(10)

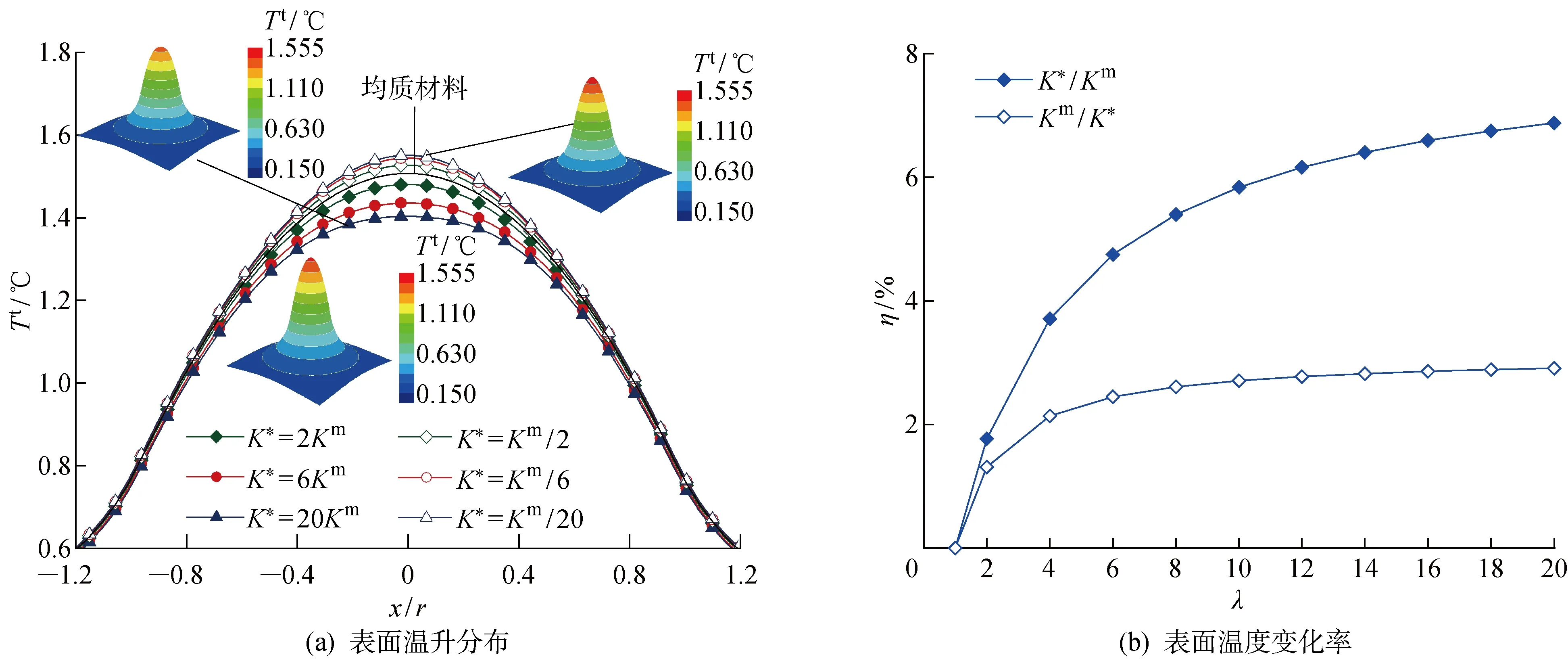
圖7 不同導熱系數增強體表面溫升分布及溫度變化率Fig.7 Distribution and change rate of surface temperature rise including an ellipsoidal reinforcement with different thermal conduction properties

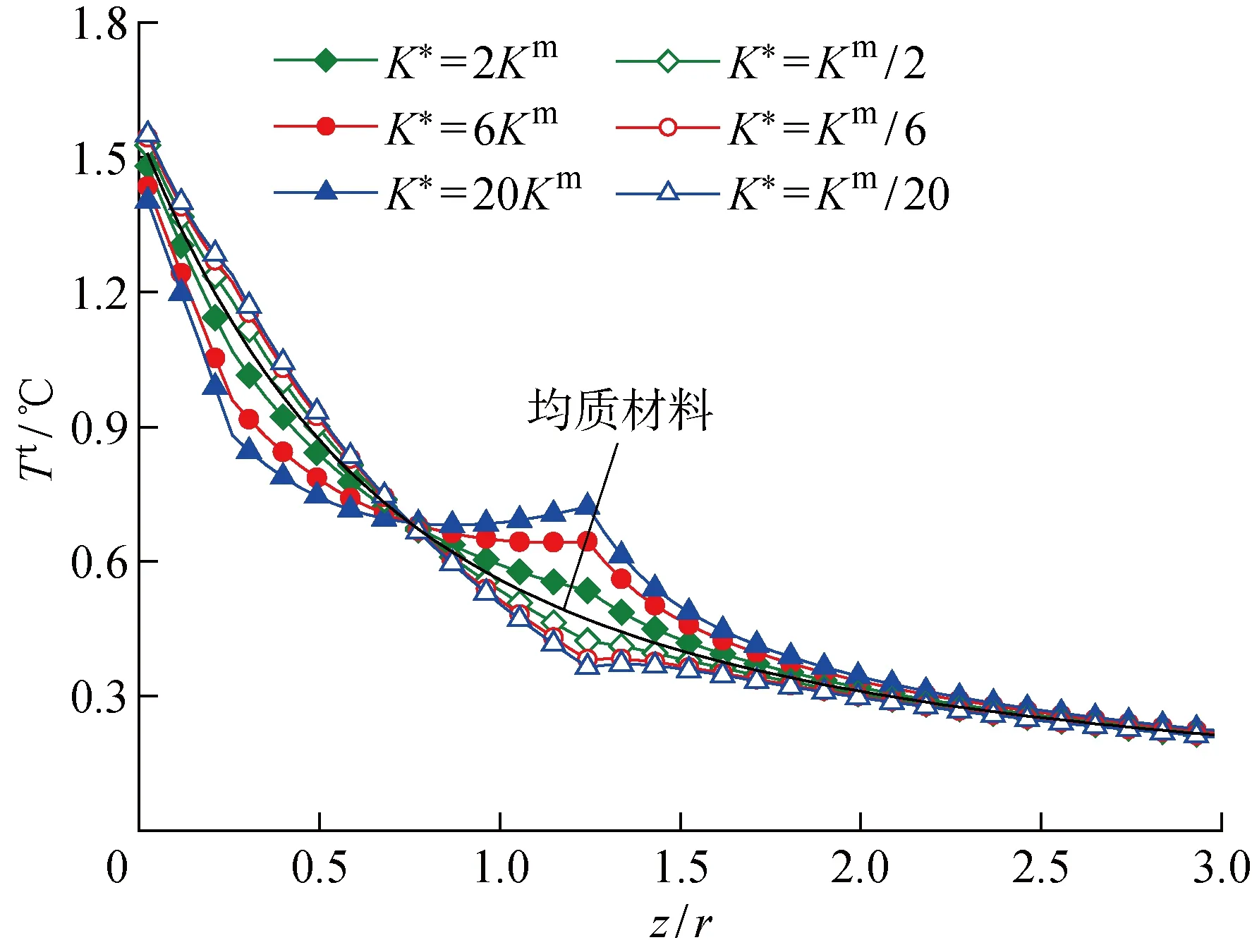
圖8 不同導熱系數增強體下表面溫升分布Fig.8 Lower surface temperature rise distribution including an ellipsoidal reinforcement with different thermal conduction properties

3.1.1導熱系數 導熱系數是影響材料熱平衡的關鍵因素，本節將通過改變增強體與基體導熱系數之比λ(λ=K*/Km或λ=Km/K*)使之從1～20之間變化，以探究顆粒增強復合材料內部熱平衡規律，結果如圖7和8所示.從圖7(a)中可以看出，當λ=K*/Km時，隨著λ的增大，表面溫升分布趨于平緩，表面溫度值逐漸減小；當λ=Km/K*時，則得到與前者相反的結論.圖7(a)中還給出了K*=20Km、K*=Km/20和K*=Km3種情況下溫度標尺相同的表面溫升三維等值線圖，可直觀地看出表面溫升情況.圖7(b)結果表明，隨著λ的增大，η先快速增長后增速逐漸放緩，且λ=K*/Km時相對λ=Km/K*增速更為顯著.圖8為圖7(a)情況對應的下表面沿z軸的溫升分布.圖中曲線表明增強體距離表面近端和遠端位置附近都會對溫度場有較大擾動，且λ越大，擾動越明顯.產生上述現象的原因在于增強體的導熱系數較基體大時，則熱量在增強體中集中，導致在增強體距表面近端處溫度相對均質材料要低，而遠端溫度相對均質材料要高.增強體導熱系數較基體小時則相反.

3.1.2深度 由于材料受摩擦熱等外部熱載荷作用時，是從表面往內部傳遞的，所以，顆粒增強復合材料內部熱平衡往往與增強體的深度位置密切相關.設置橢球增強體中心到表面的距離h∈[0.6r, 2r]，研究不同深度增強體對顆粒增強復合材料熱平衡的影響規律.圖9所示為含不同深度增強體顆粒增強復合材料表面溫升分布及溫度變化率.圖9(a)中表面溫升分布曲線表明，不論增強體導熱系數大于或小于基體，隨著增強體深度的增加，表面溫升分布都將越來越接近均質材料.在h/r=0.6時，K*=20Km和K*=Km/20兩種情況下基體表面溫升分布可從相應的三維等值線圖直觀看出.從圖9(b)中可以看出，隨著增強體深度的增加，無論其導熱系數大于或小于基體，顆粒增強復合材料表面溫度變化率都快速下降，逐漸趨近于0.上述結果表明，隨著增強體深度的增加，表面熱載荷作用對顆粒增強復合材料內部及表面溫度場擾動逐漸減小.

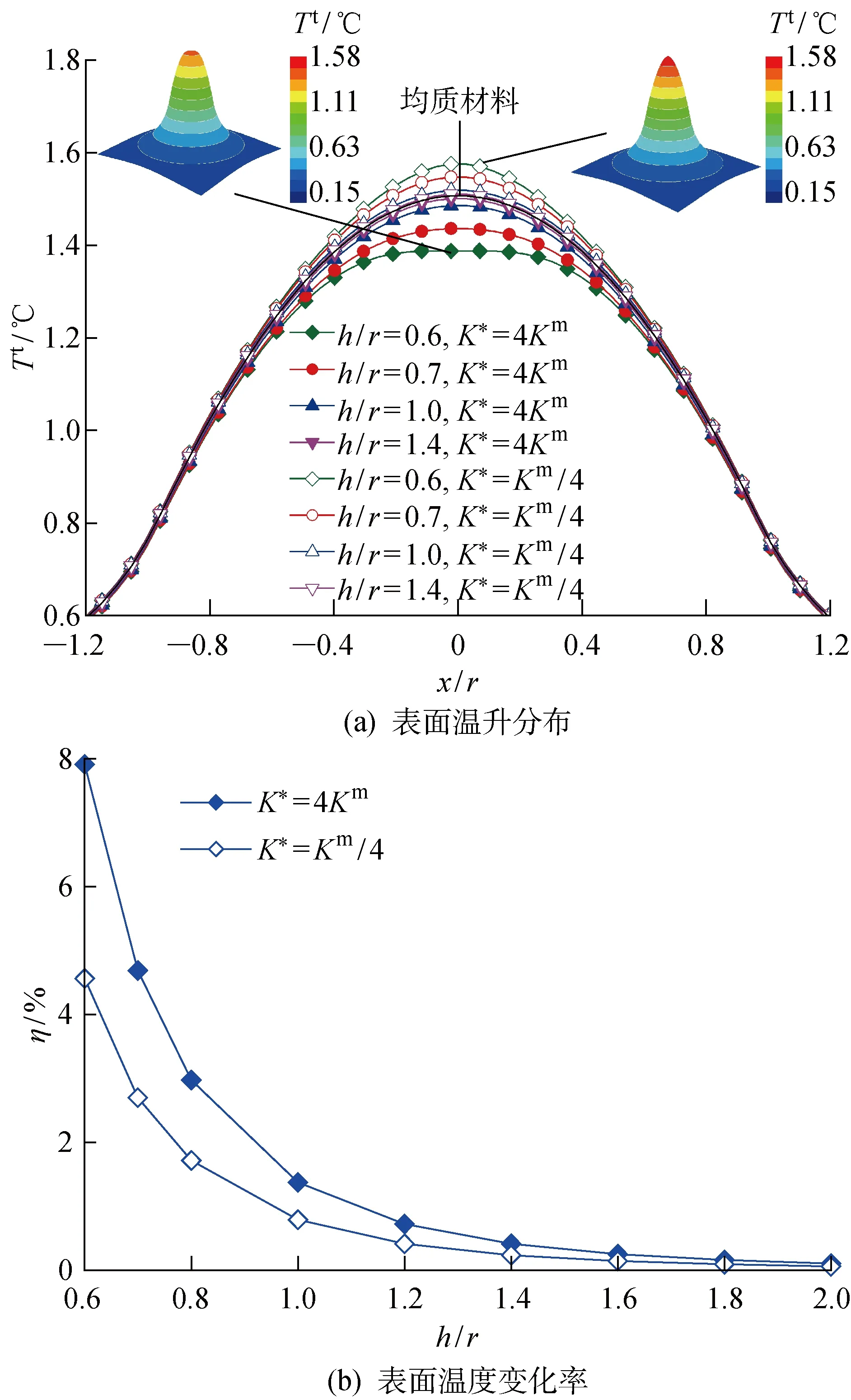
圖9 不同深度位置增強體表面溫升分布及溫度變化率Fig.9 Distribution and change rate of surface temperature rise including an ellipsoidal reinforcement at different depth locations

3.1.3朝向角度 顆粒增強復合材料中類纖維狀增強體空間朝向具有隨機性，且增強體的朝向角度已被證實對應力場會產生影響[17].本小節將改變其朝向角度，保持α=0° 和β=90° 不變，使歐拉角γ在0°～ 90° 之間變化，探究其對顆粒增強復合材料溫度場的影響規律.圖10給出了γ分別為0°、45° 和90° 時顆粒增強復合材料下表面溫升分布云圖，此時K*=4Km.由圖可知，增強體不同空間朝向將對材料溫升分布產生較大影響.從圖11顆粒增強復合材料表面溫度變化率曲線中可知，隨著γ的逐漸增大，η先減小后增大，且γ=45° 時η最小.

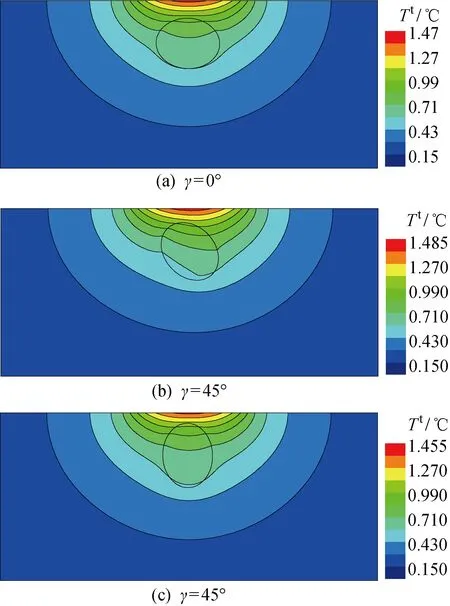
圖10 不同朝向角度橢球形增強體下表面溫升分布Fig.10 Lower surface temperature rise distribution including an ellipsoidal reinforcement with different facing angles

圖11 不同朝向角度橢球形增強體表面溫度變化率Fig.11 Distribution and change rate of surface temperature including an ellipsoidal reinforcement with different facing angles

3.2 多增強體熱平衡分析

增強體往往隨機分布于顆粒增強復合材料中.本小節考慮多個增強體之間的相互作用，進一步分析其對顆粒增強復合材料溫度場的影響.

圖12(a)為含雙球形增強體顆粒增強復合材料模型，增強體中心位于Oxz平面上，沿z軸對稱分布，且其中心到表面的距離h=0.6r.球形增強體直徑d=r，間距為l.增強體的導熱系數為K*=4Km和K*=Km/4，其余參數保持不變.改變間距l，使其在r～3r之間變化，研究顆粒增強復合材料下表面溫升分布規律.

圖12(b)和12(c)所示為利用本文所提算法求出的含不同間距雙球形增強體(K*=4Km)顆粒增強復合材料下表面溫升分布云圖.從圖中可以直觀看出不同間距的增強體對基體溫度場的影響程度不同，而且當l增大時，會使基體溫度場向周邊擴散.

圖13所示為不同間距雙球形增強體顆粒增強復合材料表面溫度變化率.圖中曲線表明，隨著l增大，η逐漸降低，且兩種材料增強體造成的η差異也在逐漸減小.

圖14(a)所示為中心位置坐標(x,y,z)服從正態分布的200個半徑為0.2r球形增強體顆粒增強復合材料模型，即

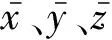
x～N(0,r2)

y～N(0,r2)

z～N(r,r2)

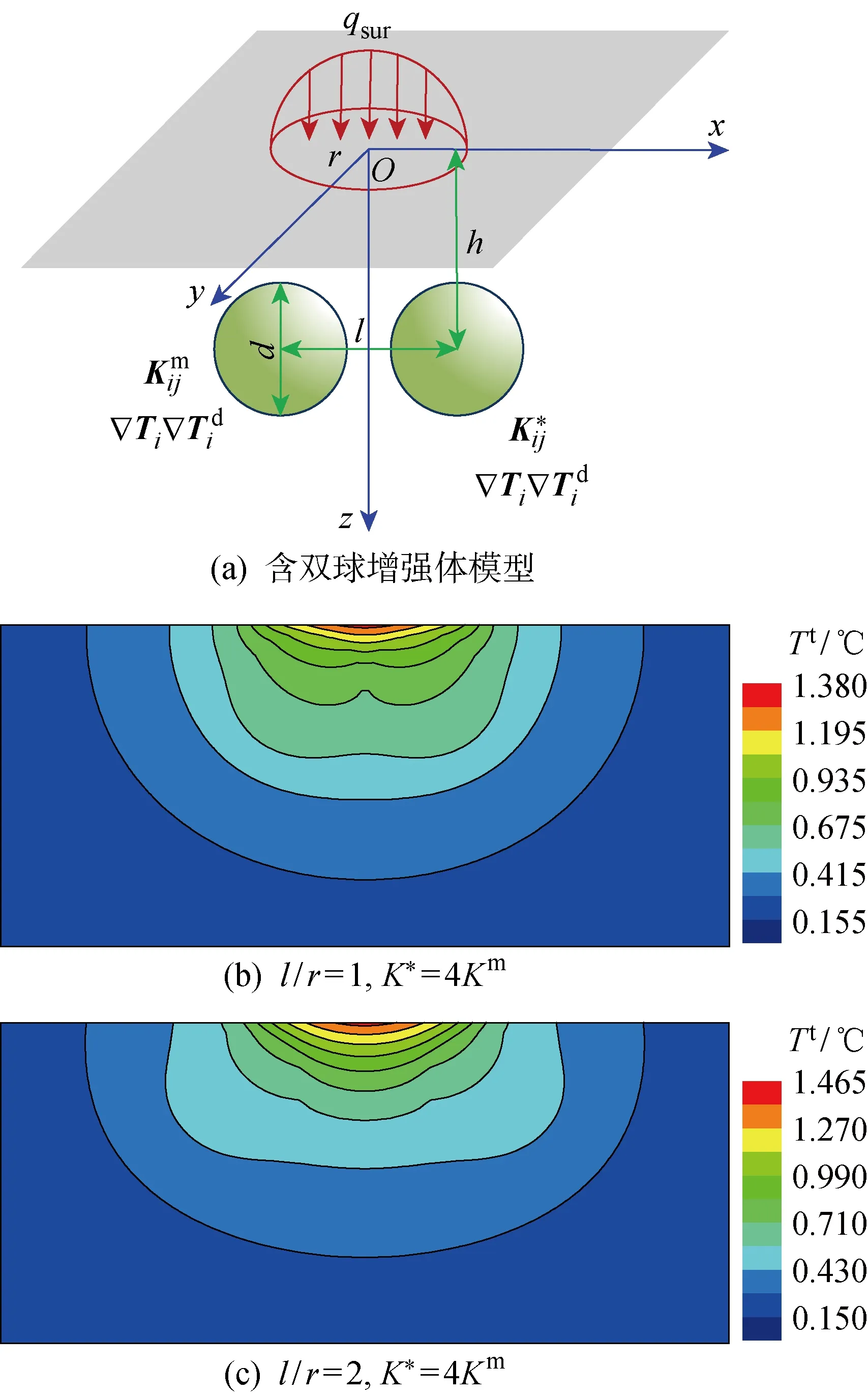
圖12 含雙球形增強體模型及下表面溫升分布Fig.12 Model including two spherical reinforcements and its lower surface temperature rise distribution

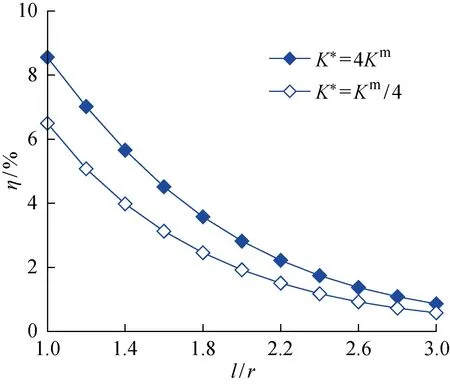
圖13 不同間距雙球形增強體表面溫度變化率Fig.13 Change rate of surface temperature including two spherical reinforcements with different distances

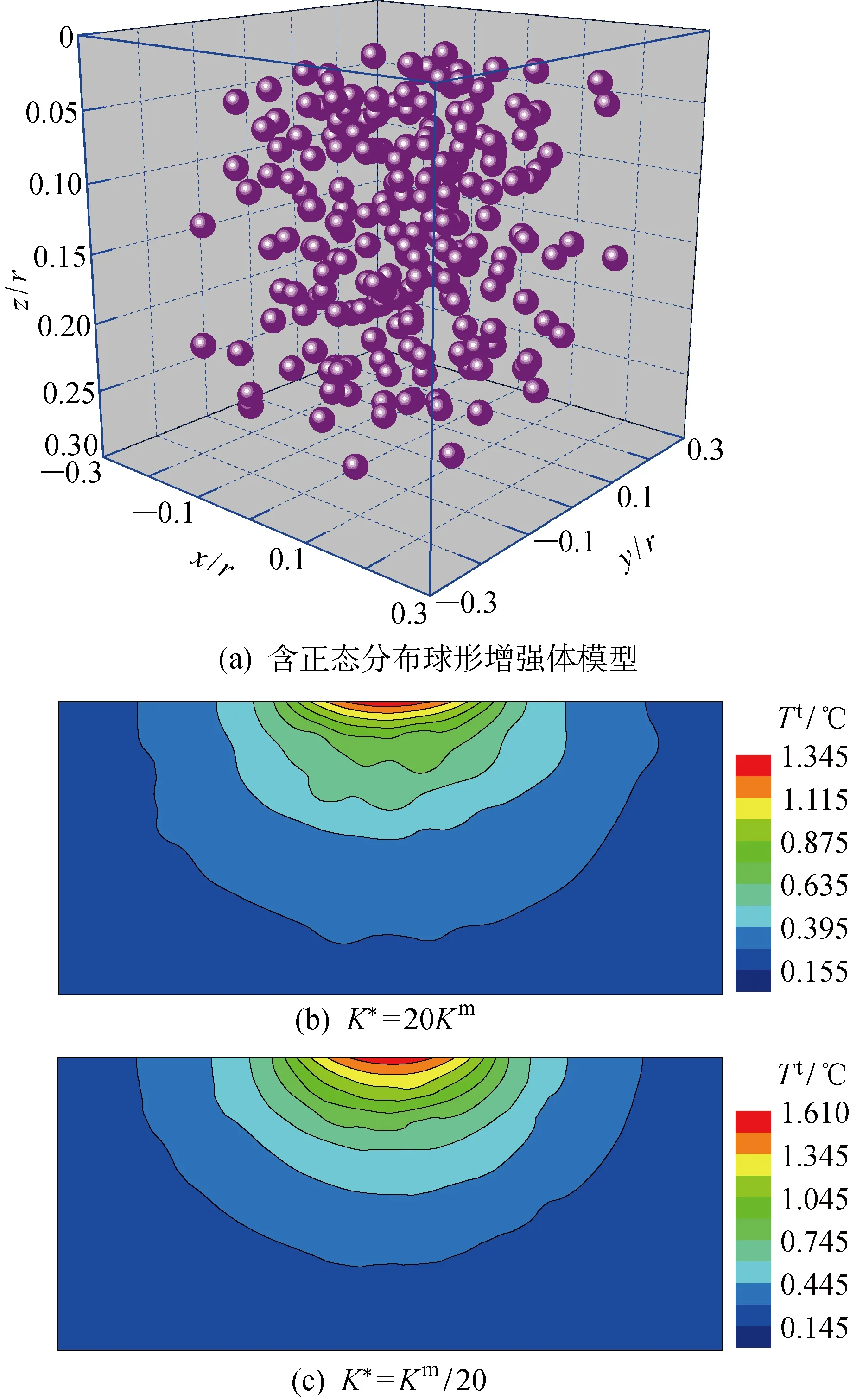
圖14 含正態分布球形增強體模型及下表面溫升分布Fig.14 Model including spherical reinforcements in normal distribution and its lower surface temperature rise distribution

增強體導熱系數為K*=20Km和K*=Km/20，其余參數參照前例，計算結果如圖14(b)和14(c)所示.從圖中可以看出，隨機分布的增強體對材料下表面溫升分布擾動較大，且位置接近表層的增強體對表面溫度及周圍溫度影響較為顯著，而較深的增強體對溫度場的擾動則相對較小.對比K*=20Km和K*=Km/20兩種情況，可發現后者溫度變化范圍更廣，且具有較大的溫升，說明即使是將增強體分散于基體中，其導熱系數對基體溫升分布也具有較大影響.

4 結論

(1) 本文提出了一種熱載荷作用下顆粒增強復合材料熱平衡數值建模方法.對于單橢球增強體模型，增強體導熱系數與基體差異越大，越容易造成表面溫度變化率增大.因此在顆粒增強復合材料制備過程中，增強體熱屬性不宜與基體差異太大，否則影響表面溫度變化率，從而導致材料表面性能退化.

(2) 單橢球形增強體越靠近表面高溫度區時，其對基體表面溫度擾動越大.此外，單橢球形增強體朝向會對溫度場產生較大影響，在本文設定情況下，歐拉角γ在45° 左右時對表面溫度的影響最小.工程實際中，顆粒增強復合材料增強體的分布應盡量遠離受熱載荷表面區域，且橢球/纖維狀增強體歐拉角γ應在45° 左右.

(3) 雙球形增強體間距增大，表面溫度變化率逐漸降低且由不同導熱系數增強體造成的顆粒增強復合材料表面溫度變化率差異也在逐漸減小.分布于顆粒增強復合材料中的增強體會對基體溫度場造成擾動，且越靠近表面的增強體造成的擾動越顯著.

本文所提材料溫升分布求解模型可有效考慮材料微觀結構對熱載荷作用下材料內部熱平衡的影響，為顆粒增強復合材料及其他材料散熱、吸熱等功能需求為導向的內部微觀結構優化設計提供理論指導.耦合材料彈、塑、電、磁等不同場的求解模型，可進一步求解不同外載聯合作用下非均質材料復雜工程力學問題.