針對執行器非光滑反向間隙?飽和的柔性立管邊界控制

趙志甲 任志剛

在深海勘探開發生產中,海洋柔性立管作為連接海面作業平臺與海床井口的關鍵構件[1].在風、浪、洋流等外部載荷作用下,海洋立管會產生振動現象,而長期的振動則是造成柔性立管疲勞破損的主因[2?4].因此,開展先進的海洋柔性立管振動主動控制系統研究,對延長立管使用壽命、提高生產效率和保證海洋油氣生產安全具有重要的理論和實際意義.

從數學的觀點看,具有振動的海洋柔性立管系統可認為是典型的無限維分布參數系統[5?11].其動力學往往建模為耦合的偏微分–常微分方程,這使得現有許多對傳統剛性系統成熟的方法不能直接應用.對海洋柔性立管振動控制的研究主要包括模態控制和邊界控制.模態控制是基于提取的有限維受控子系統進行控制設計,而忽略掉的高頻模態可能導致系統產生控制溢出效應.邊界控制能克服上述方法的缺點,且容易由系統機械能相關的Lyapunov 函數得出,因此邊界控制與其他控制技術如PID 控制、魯棒控制、自適應控制、反步控制、輸出反饋控制等相結合的方法廣泛應用于柔性立管系統的振動控制領域[12?16].上述研究僅僅局限于柔性立管系統的振動控制,而這些方法將不適用于具有輸入非線性特性的柔性立管系統.

在實際的海洋油氣生產環境中,柔性立管系統除了受到風浪擾動和海洋洋流分布式擾動影響外,其面臨的情況可能會比之前研究的問題更加復雜.如系統固有的物理約束和執行器的約束將使得系統產生死區、飽和、磁滯、反向間隙等不光滑的非線性特性[17?20].而這些不光滑的非線性特性將會限制系統的瞬態性能,更為甚者,將會致使系統不穩定.因此,需要將這些不光滑的非線性約束特性考慮在控制設計中.為了解決海洋柔性立管系統的輸入非線性約束問題,一些學者基于立管原始無限維模型探索了不同的邊界控制方法[13,21?24].文獻[13]面向具有系統不確定性、輸出約束和輸入飽和的海洋立管系統,基于反推技術研發了障礙邊界控制策略以抑制振動、補償系統不確定性以及處理系統的輸入輸出限制.文獻[21]針對具有執行器輸入飽和非線性約束和外部海洋擾動的海洋柔性立管系統,在頂端構建邊界控制器以穩定其在平衡位置的小鄰域并利用輔助系統補償執行器飽和的影響.文獻[22]設計了魯棒自適應控制器用以穩定具有參數不確定性和輸入受限的海洋柔性立管系統.文獻[23]采用光滑的雙曲正切函數、Nussbaum 函數和輔助系統設計邊界控制器以抑制立管振動并限制控制輸入在給定范圍內,該方法解決了文獻[21?22]中應用符號函數限制控制輸入所帶來的震顫問題.文獻[24]引入輔助函數和變量設計邊界控制器來實現立管的振動減弱并消除混合的死區?飽和非線性約束影響.然而,這些成果僅僅解決了柔性立管系統執行器輸入飽和或輸入飽和?死區非線性約束問題,而對于具有輸入反向間隙?飽和非線性約束的柔性立管系統,上述方法將不能適用.

本文針對執行器非光滑反向間隙?飽和約束特性的深海柔性立管系統(如圖1 所示),首先將反向間隙?飽和約束轉換成虛擬的輸入飽和約束,其后引入輔助系統并采用Lyapunov 理論,構建邊界控制以抑制柔性立管的振動并消除飽和非線性約束的影響.隨后,證明了閉環系統在Lyapunov 意義下的一致有界穩定性.最后,通過數值仿真,驗證了本文所提出控制能處理非光滑反向間隙?飽和約束非線性影響,也能有效抑制立管系統振動.

1 問題描述和預備知識

注1.本文作如下簡寫:

1.1 立管動力學模型

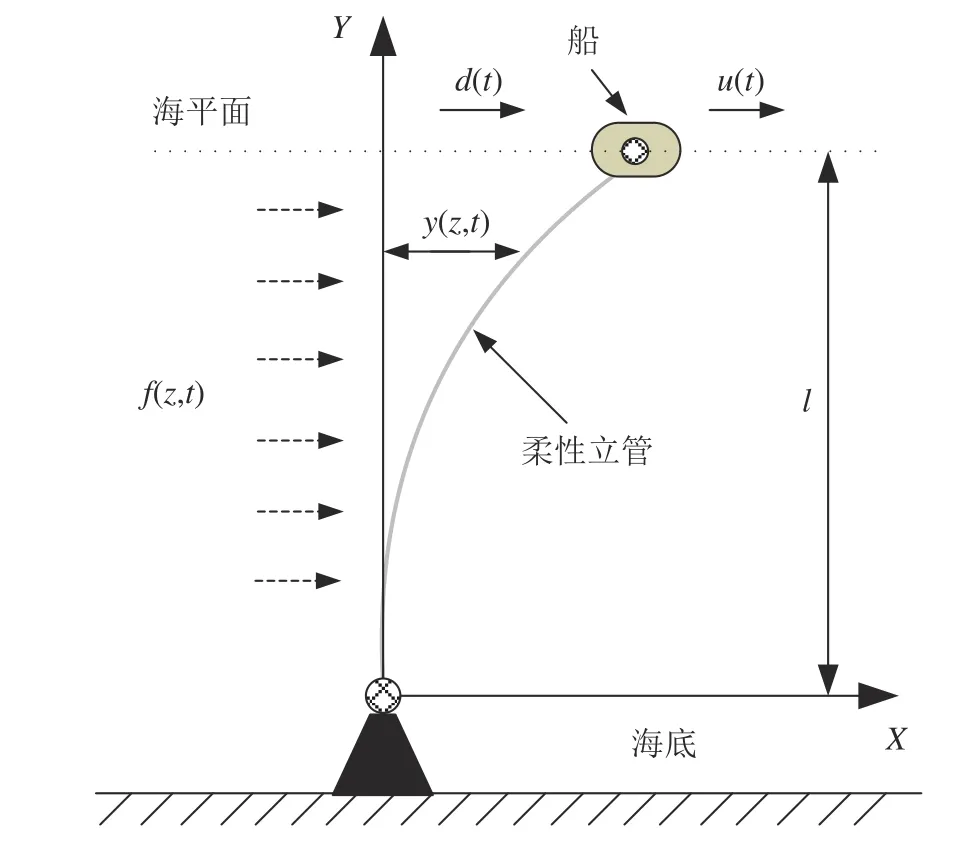
圖1 柔性立管系統Fig.1 Flexible riser system

深海柔性立管系統如圖1 所示,其中l為立管的長度,y(z,t)為立管在位置z時刻t的偏移量,f(z,t)為海洋洋流分布式擾動,d(t)為外部環境擾動,u(t)為邊界控制輸入.

本研究所考慮立管系統動力學描述如下[1]:

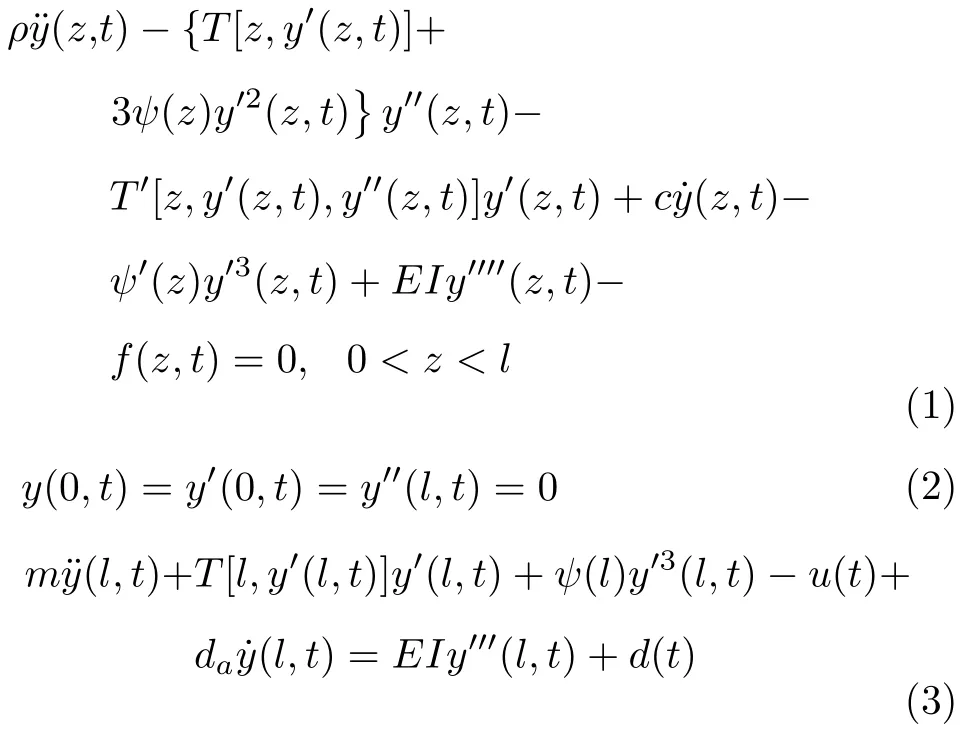
其中,ρ,c和EI分別為立管的單位長度質量、阻尼系數和彎曲剛度,da和m為船的質量和阻尼系數,為立管的時空變化張力,表示為

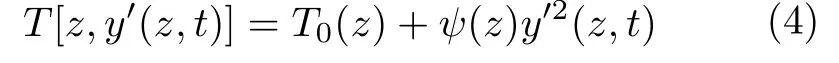
其中,T0(z)>0為初始張力,ψ(z)≥0 為非線性彈性模量.

執行器輸入飽和非線性描述為[25]

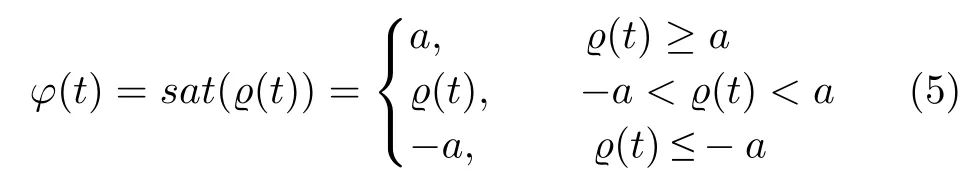
其中,a>0 為飽和界限.

執行器輸入反向間隙非線性描述為[24]

其中,b>0 為反向間隙參數.

由輸入飽和與反向間隙的表達式(5)和式(6)可知,系統的非線性特征是相當復雜的,因此很難直接對其處理.根據文獻[25],可知輸入飽和與反向間隙可轉換并表示為一個虛擬的輸入飽和.因此,為解決虛擬的輸入非線性問題,我們引入D的右逆D+為

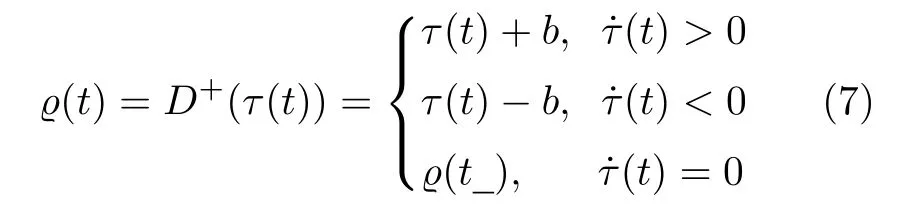
根據上面的分析和文獻[25],我們可得混合的輸入飽和?反向間隙非線性特性可描述為

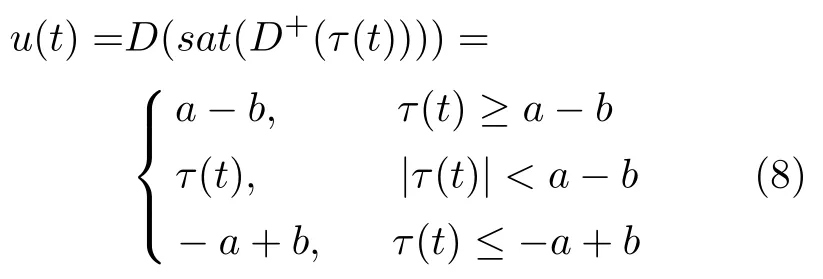
由式(8)可知,我們可將系統的輸入飽和?反向間隙非線性視為一個輸入飽和來處理.

1.2 預備知識

引理1[26].設χ1(z,t),χ2(z,t)∈R,φ>0,其中(z,t)∈[0,l]×[0,+∞),則

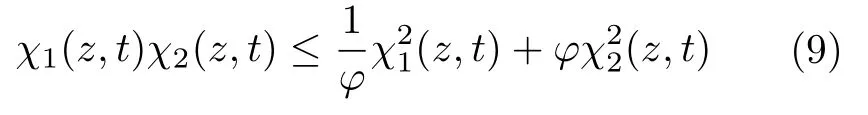
引理2[26].設χ(z,t)∈R為定義在(z,t)∈[0,l]×[0,+∞)的函數,且滿足χ(0,t)=0,?t ∈[0,+∞),則

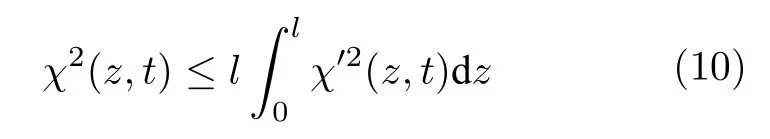
假設1.假定存在常數F,D ∈R+, 使得|f(z,t)|≤F,?(z,t)∈[0,l]×[0,+∞),|d(t)|≤D,?t ∈[0,+∞).這個假設是合理的,由于f(z,t)和d(t)是有限能量的,因此是有界的[21?24].

假設2.假定存在正常數,使得

假設3.對于新的輸入飽和表達式(8),假定存在一個正常數?使得|△u|≤?,其中,△u=u(t)?τ(t).

2 控制器設計

本節將引入輔助函數和輔助系統用于構建邊界控制器以抑制立管振動并消除輸入非線性影響.

2.1 邊界控制器

首先,設計輔助系統為

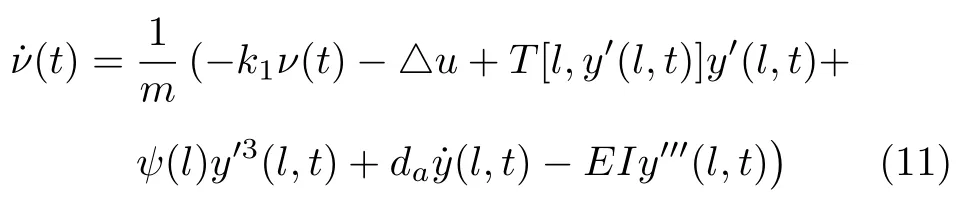
其中,ν(t)為輔助系統的狀態變量,k1為正常數.

為便于分析閉環立管系統的穩定性,定義如下輔助變量

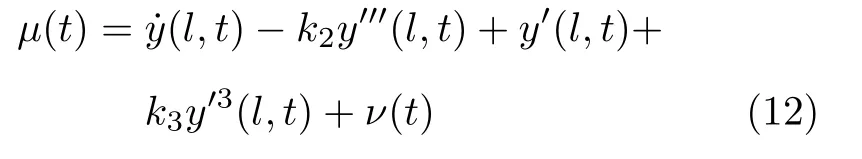
其中,k2,k3為正常數.

對式(12)求導,代入式(3)和式(11),可得

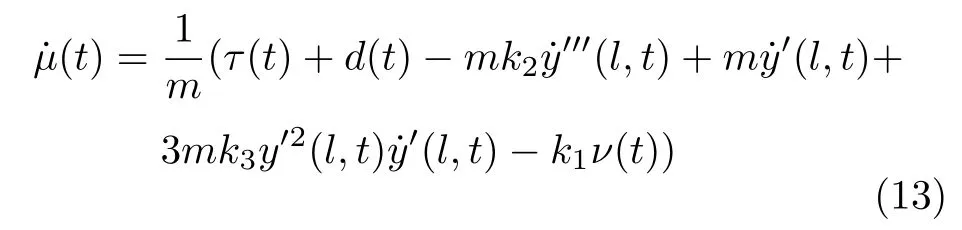
根據上述分析,提出控制律τ(t)為

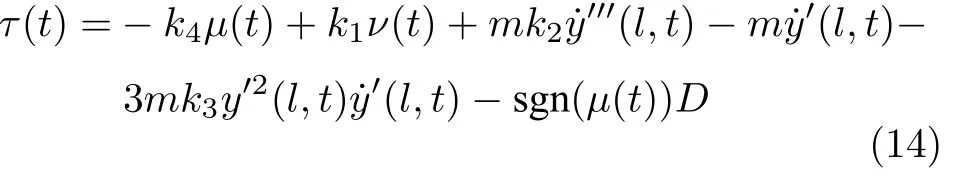
其中,k4為正常數.

注2.所設計的控制器(14)是由可獲得的邊界信號組成的,其中分別可由剪切力傳感器、傾角計和位移傳感器獲得.此外,控制器中這些信號的一階時間微分信號分別可對已獲得信號進行后向差分算法得到[21?24].

選取如下Lyapunov 函數為

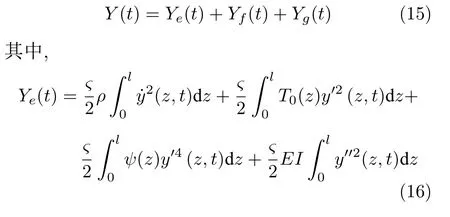
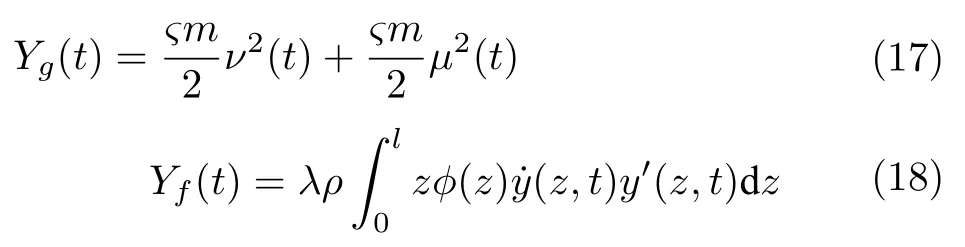
其中,?,λ>0 .

引理3.選取的Lyapunov 函數(16)是一個正定的函數:

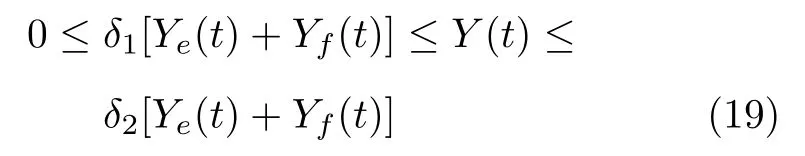
其中,δ1>0,δ2>1 .

證明.根據引理1,式(18)可放縮為

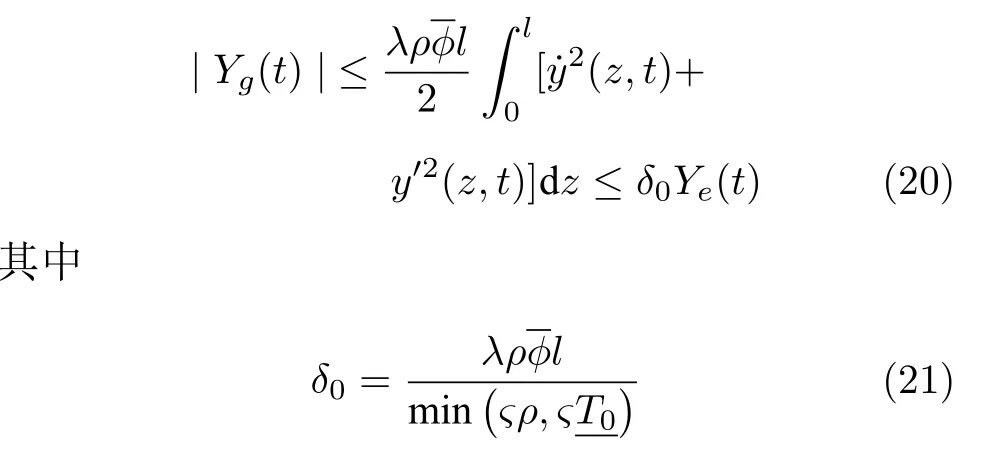
通過恰當地選取?和β得出

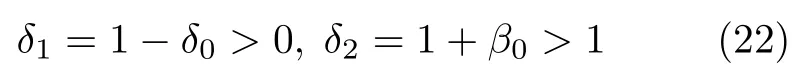
式(22)表明 0<δ <1,應用式(21)可得

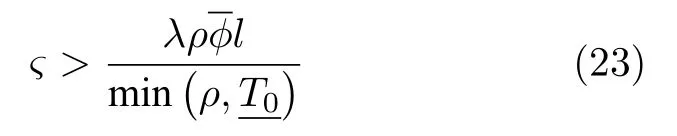
重排式(20),有

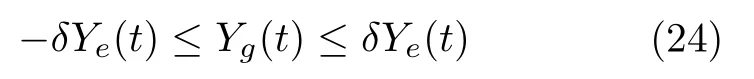
將式(22)代入式(24)得出

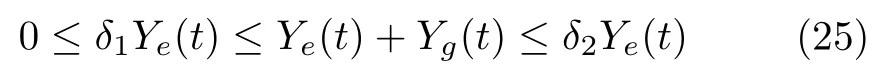
結合式(15),有

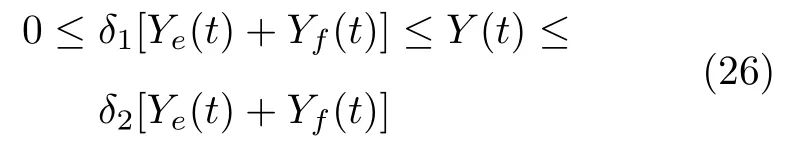
其中,δ1>0,δ2>1 . □

引理4.選取Lyapunov 函數(16)的導數是有上界的:

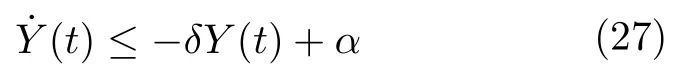
其中,δ,α>0 .

證明.對式(16)求導,可得:

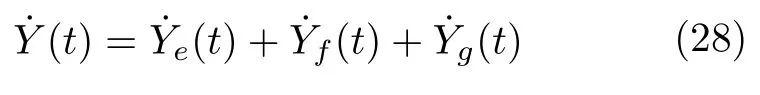
將式(16)求導,代入式(1)并應用引理1,可得

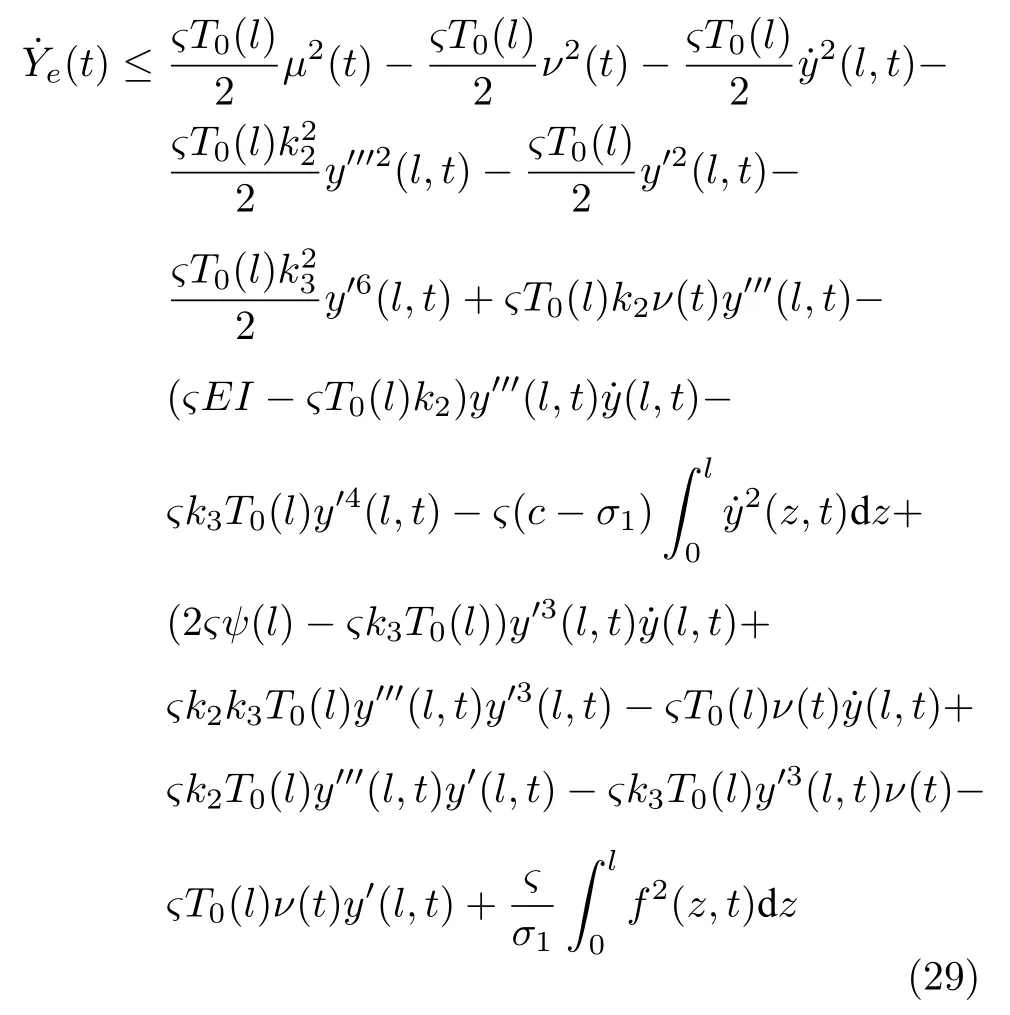
其中,δ1>0 .

對Yf(t)求導,代入式(11)和式(14),應用引理1,可得

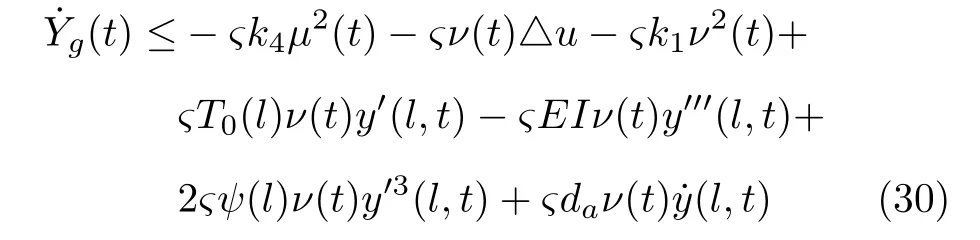
對Yg(t)求微分,代入式(4)并利用引理1,有

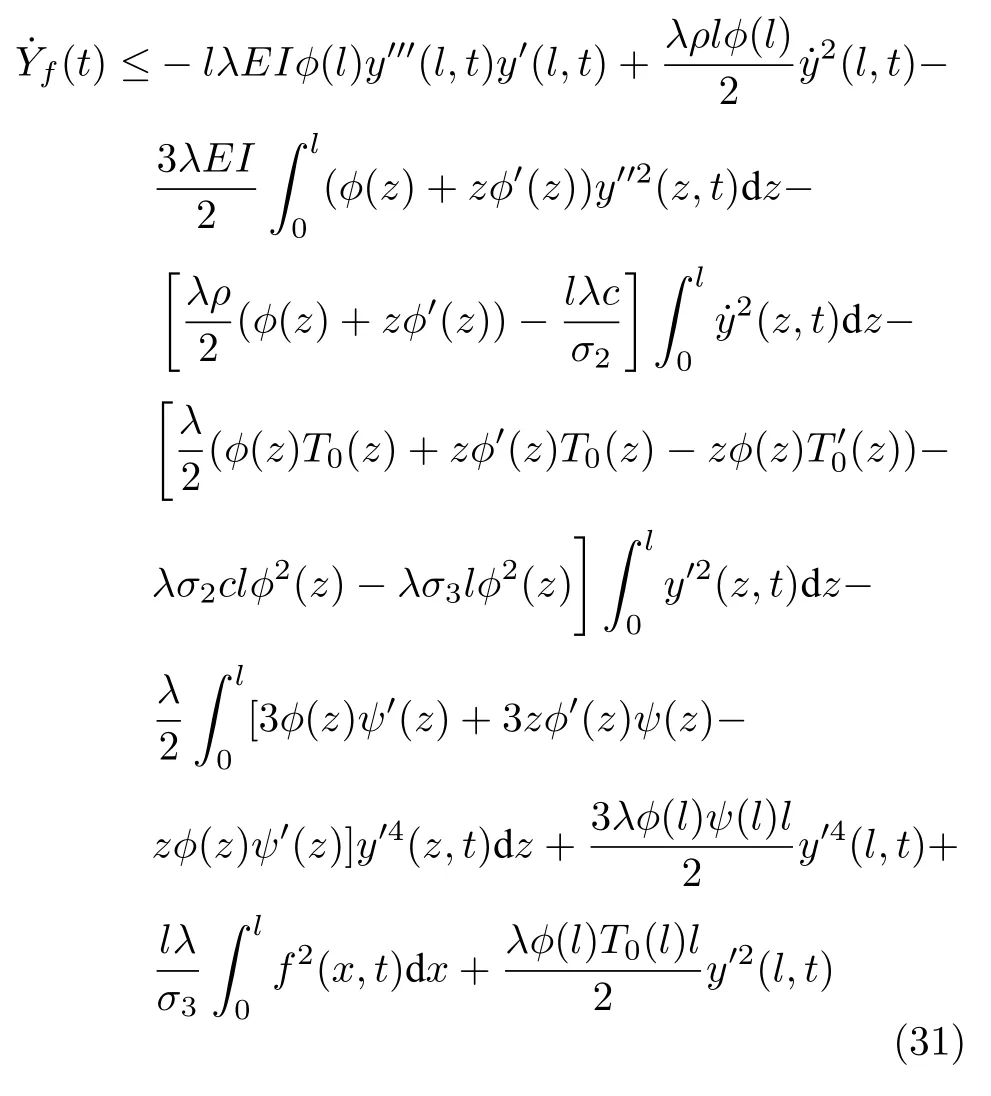
其中,σ2,σ3>0 .

將式(29)和式(30)代入式(28),應用引理1,可得

其中,σ4～σ11>0,選擇恰當的參數值?,λ,ki,i=1,···,4,δj,j=1,···,11,滿足下列條件:

結合式(33)～(44),可得

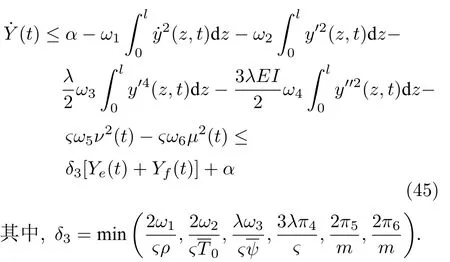
根據式(26)和式(45),有

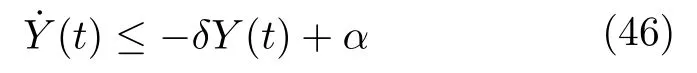
其中,δ=δ3/δ2. □

定理1.針對執行器非光滑反向間隙?飽和約束特性的深海柔性立管系統,如果系統初始條件是有界的且所選取參數滿足約束條件式(33)～(44),在設計控制器(14)、假設1 和假設2 作用下,閉環系統是一致有界穩定的.

證明.將式(27)乘以 e?t,得出:

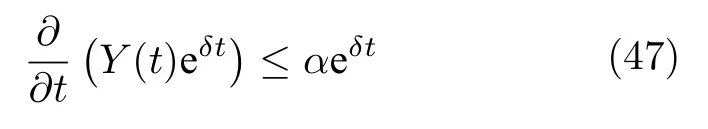
積分上式并變換,有:

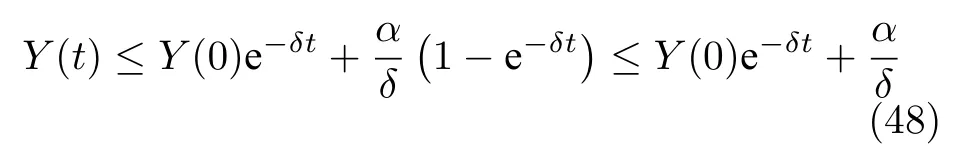
求助于Ye(t),式(19)和引理2,可得

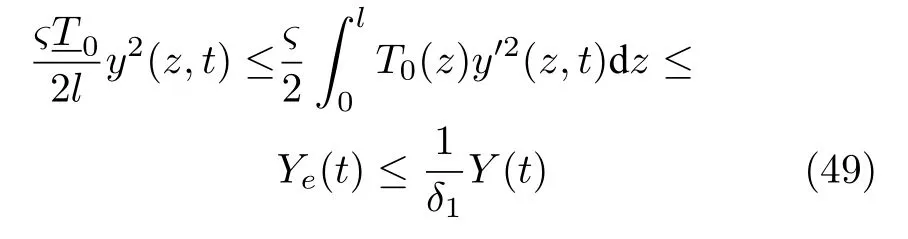
將式(48)代入式(49),產生

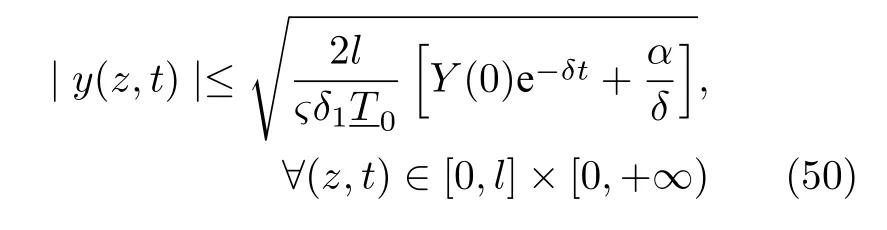
進一步得出

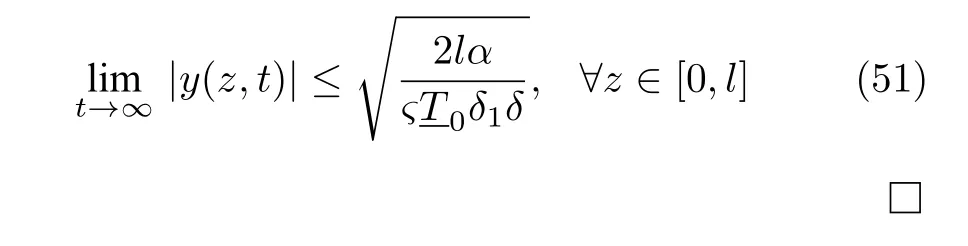
3 數值仿真

為驗證所設計控制器的性能,本節在MATLAB軟件中采用有限差分法[27?30]來近似閉環系統的數值解.柔性立管系統的參數為l=1 000 m,ρ=500 kg/m,=9.6×106kg,da=1 000 Ns/m.系統的初始條件描述為:

外部環境擾動d(t)為

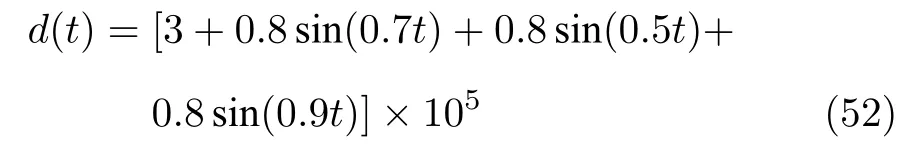
柔性立管系統在自由振動時,即u(t)=0,圖2給出了其時空的表示.在所示設計控制器(14)作用下,選取控制設計參數k1=1×107,k2=1/60,k3=1/225,k4=5×108,a=1×106,b=5×106,立管三維響應顯示在圖3 中.圖4 則給出了立管中部頂端 (x=1 000 m)的二維偏移圖,圖5 和圖6 分別描繪了所設計的控制命令和反向間隙?飽和控制輸入.

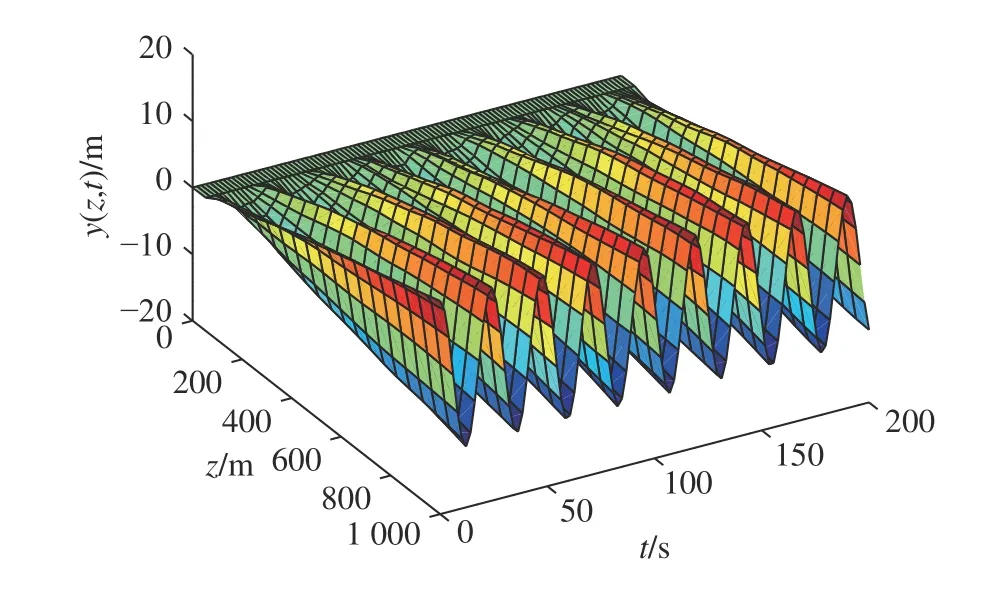
圖2 未受控的立管偏移量Fig.2 Displacement of the uncontrolled riser

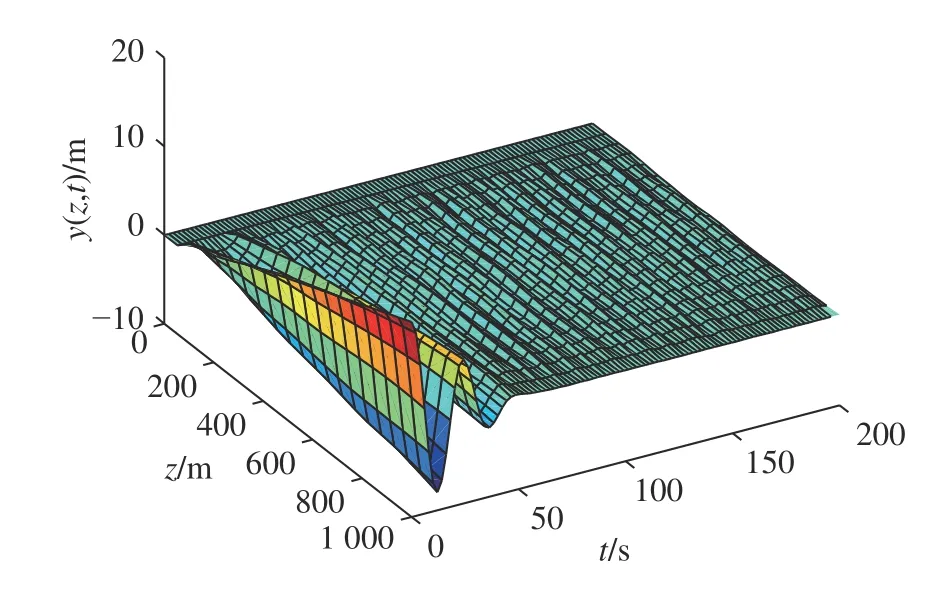
圖3 受控的立管偏移量Fig.3 Displacement of the controlled riser

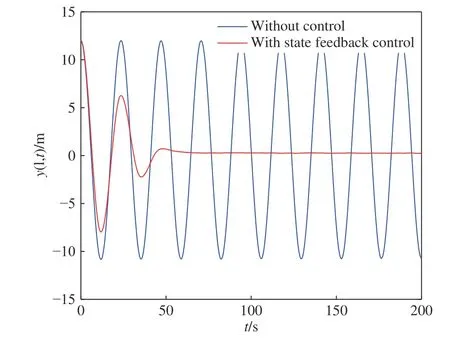
圖4 立管的端點偏移量Fig.4 Endpoint displacement of the riser

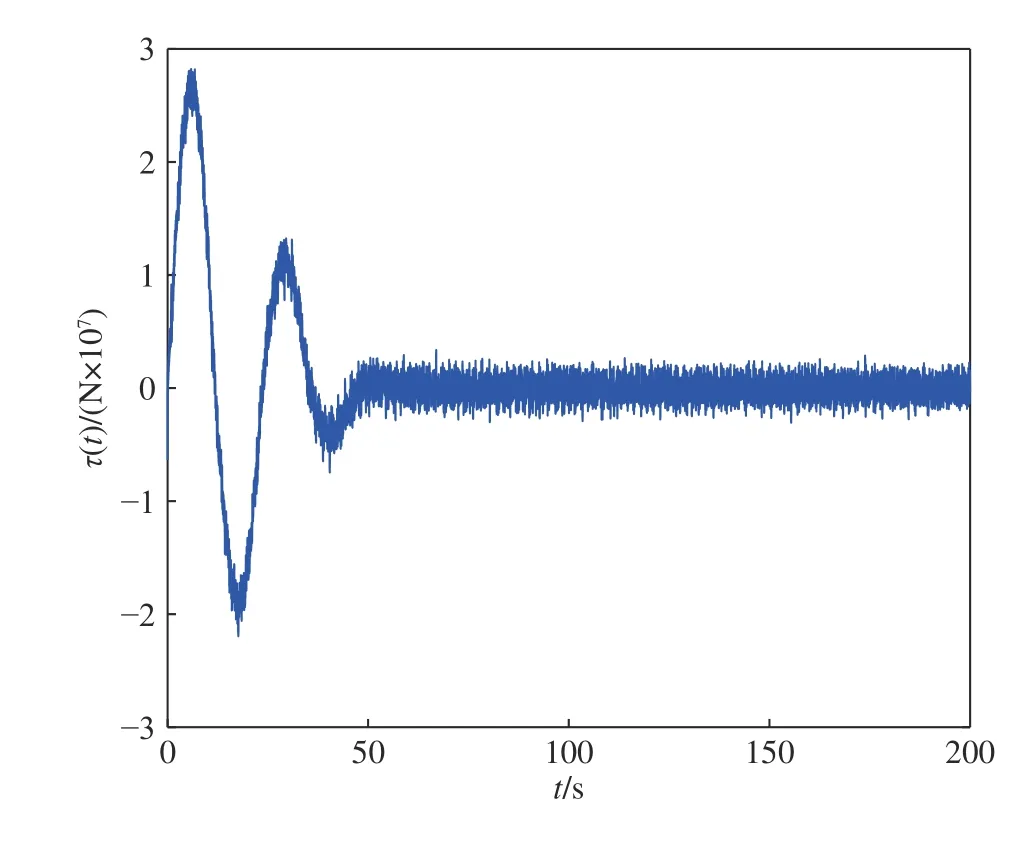
圖5 設計的控制命令Fig.5 Designed control command

仿真圖2 和圖3 表明,在外部擾動和執行器非光滑反向間隙?飽和約束條件下,所設計控制器(14)能有效抑制立管振動;由仿真圖4 可得,立管端點的偏移量穩定在平衡位置附近的小鄰域;仿真圖5和圖6 得出,控制器的輸入是非線性的,執行器非光滑反向間隙?飽和約束特性也相當地明顯.根據上述分析,可得如下結論:由于混合的輸入非線性影響,立管的振動偏移量需要相對長的收斂時間;本文所構建的控制策略能較好地處理執行器非光滑反向間隙?飽和約束并能有效地抑制立管振動.

4 結論

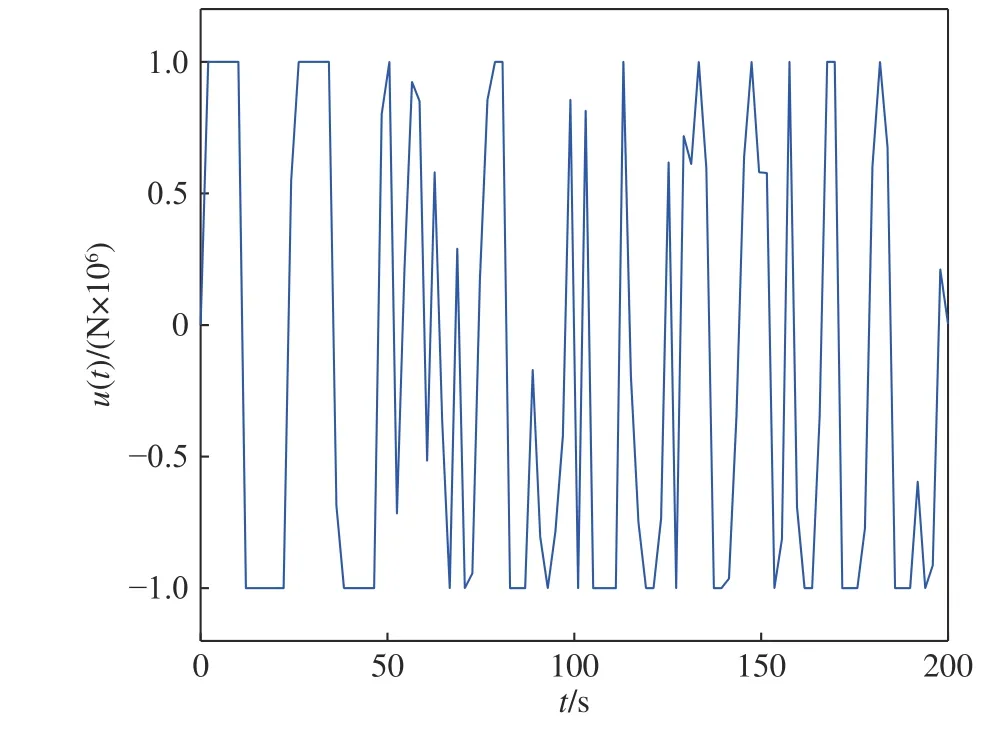
圖6 非線性的控制輸入Fig.6 Control input with nonlinearities

本文解決了具有執行器非光滑反向間隙?飽和約束特性的深海柔性立管邊界控制問題.首先,基于Lyapunov 理論和邊界控制技術,采用輔助系統和函數在立管頂端構建了邊界控制器以實現立管系統的振動抑制和輸入非線性的補償.其后,應用嚴格的分析且沒有離散化或簡化系統的偏微分方程動力學,證明了受控系統的一致有界性.最后所呈現的仿真結果驗證了提出控制能較好地穩定立管系統并有效消除執行器非光滑反向間隙?飽和約束影響.下一步值得探索的研究方向可以為海洋柔性立管系統的有限時間穩定[31]以及基于不確定性和干擾估計[32]的控制設計.