基于性能指標約束的一類輸入死區非線性系統最優控制

郭子杰 白偉偉 周 琪 魯仁全

不確定非線性系統控制問題一直是控制領域內研究的熱點和難點[1?8].以模糊邏輯系統,神經網絡為基礎的自適應控制設計方法,打破了以往系統中非線性函數要滿足某些限定條件或參數化的限制[1],解決了不滿足匹配條件及不確定的非線性系統的控制器設計問題.并廣泛應用于純反饋和嚴格反饋的單輸入單輸出系統[2?3],多輸入多輸出系統[4?5],以及多智能體系統[6]中.值得注意的是,基于backstepping 技術的控制設計方法在每一步都需要對已設計的虛擬控制器進行反復求導,從而產生“計算爆炸”問題.而動態面控制技術通過在backstepping 設計的每一步中引入一階低通濾波器,有效地避免了這一問題[9].在此基礎上,文獻[10]提出一種命令濾波方法,利用誤差補償機制消除動態面技術中濾波誤差對系統性能的影響.上述工作為不確定非線性系統控制提供了一種簡便化,結構化的方法,但以上成果均沒有考慮最優控制問題.

最優控制是一類考慮系統控制性能和節能效應的控制策略[11].傳統的動態規劃(Dynamic programming,DP)采用按照時間階段逆向遞推的方法有效解決了最優控制問題[12],但其后向求解的模式往往會導致“維數災”現象的發生[13].自適應動態規劃(Adaptive dynamic programming,ADP)方法作為DP 方法的近似解法,彌補了DP 方法的不足,為求解復雜非線性系統最優控制問題提供了新的思路[14].Murray 等[15]首先針對連續系統提出了一種迭代ADP算法,并從數學上證明了該算法的可行性.Vamvoudakis 等[16]提出了基于策略迭代的在線ADP 方法,克服了迭代ADP 算法無法適應系統變化的缺點.上述的研究成果對ADP 理論的發展具有里程碑的意義.為了保證系統運行時的穩定性,文獻[15?16]所提出的方法要求給定一個初始穩定的控制策略.針對此問題,Zargarzadeh 等[17]提出一種基于單網絡評價技術的在線ADP 算法,并采用新的參數訓練方法,突破了初始穩定控制策略的限制.近年來,ADP 受到國內學者的廣泛關注[18?22],已經成為一種重要的優化控制方法.

目前,采用ADP 方法研究非線性系統的最優控制問題已經取得了一系列研究成果,然而針對帶有輸入死區和指定性能約束條件的非線性系統所做的研究較少.事實上,死區作為一類非光滑非線性函數經常出現在機械連接,液壓制動器和傳感器等實際工程系統中,極大地影響系統的性能,甚至引起系統不穩定[23].對此,文獻[24?25]借助死區的斜率來解決輸入死區問題.另一方面,工程中希望控制器不僅能夠保證系統穩定,而且使系統跟蹤誤差在一定條件下收斂.文獻[26]通過預先設定跟蹤性能函數,提出一種指定性能方法,使得系統的跟蹤誤差保持在兩個指定性能函數組成的有限范圍內,解決了控制器設計參數調節難的問題.

基于以上討論,本文針對一類考慮指定性能和具有輸入死區約束的嚴格反饋非線性系統,提出一種自適應模糊最優控制方法.本文的主要工作如下:1)結合命令濾波技術和backstepping 方法設計了一種前饋控制器,與文獻[19,27]的方法相比,本文采用命令濾波技術不但能克服“計算爆炸”問題,而且能補償濾波器誤差,取得更好的控制效果.2)設計了一種新的ADP 結構對誤差系統進行優化,利用單網絡在線逼近器求解近似最優控制器.3)本文解決了一類考慮輸入死區和指定性能約束的非線性嚴格反饋系統的優化控制問題.最后,通過實例仿真驗證所提控制方法的有效性.

1 問題描述

考慮一類嚴格反饋系統:

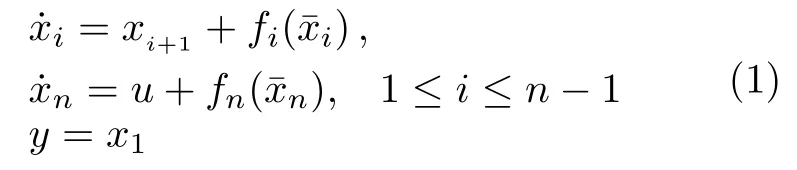
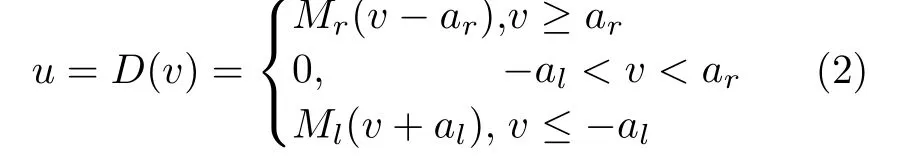
其中,v∈R是死區輸入信號,Mr和Ml表示死區的斜率,al和ar是斷點,Mr,Ml,ar,al都是正常數.

假設1[24].存在一個正常數?滿足|v|≤?.

假設2[25].給定的參考信號x1d及其一階導數是光滑的、已知的且有界.

死區輸入(2)可簡化為

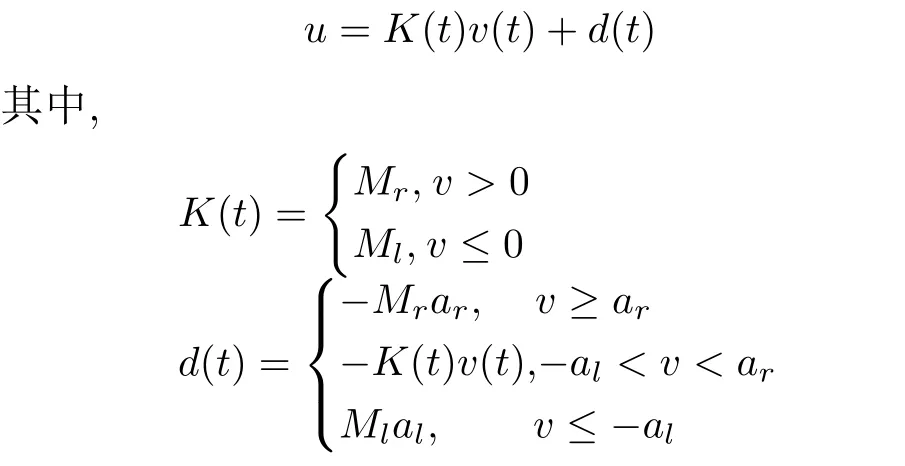
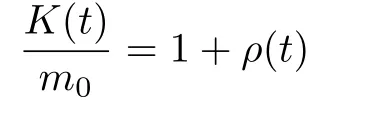
其中,ρ(t)是分段且有界的函數,滿足

根據以上討論,可得

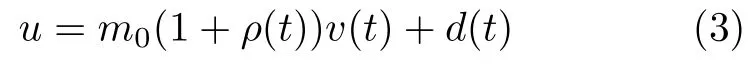
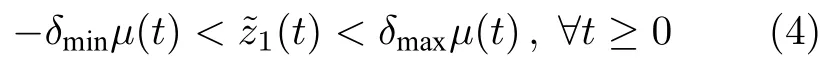
則稱系統的暫態性能滿足指定性能的要求.其中,δmin,δmax>0 是可調節的參數,指定性能函數取為μ(t)=(μ0?μ∞)e?nt+μ∞,函數μ(t)是嚴格單調遞減的函數,n>0,μ0=μ(0),μ∞=limt→∞μ(t),那么μ0>μ∞>0,而且滿足δmaxμ(0).上面不等式可以等價于以下等式

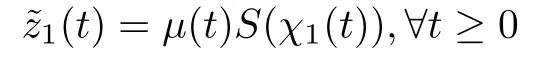
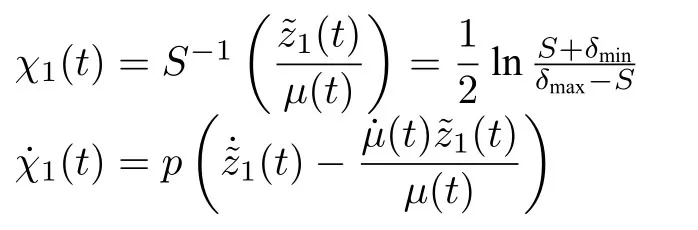
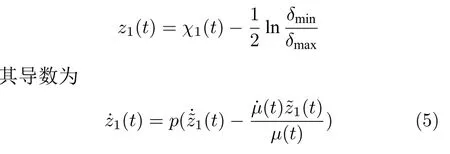
本論文的控制目的:針對一類考慮指定性能和具有輸入死區約束的非線性嚴格反饋系統設計一種自適應模糊最優控制器,保證閉環系統中所有信號都是一致最終有界的,誤差信號收斂到以“0”為中心的鄰域內,并且滿足指定性能要求,同時代價函數達到最小值.

引理1[19].對任意給定的精度? >0,都存在模糊邏輯系統wT?(Z)能逼近任意連續的非線性函數F(Z), 使得F(Z)=wT?(Z)+?(Z), 其中|?(Z)|≤?,這里F(Z)是定義在緊集 ?Z ∈Rq上的函數,w是理想權重向量,定義為

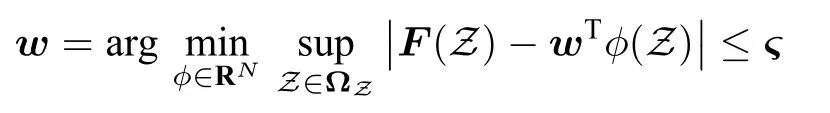
引理2[19](Young's 不等式).對于任意x,y ∈Rn,有以下不等式成立:

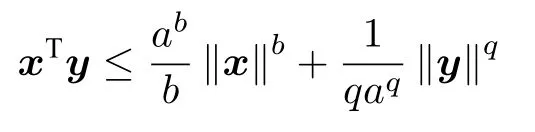
其中,a>0,b>1,q >1且 (b?1)(q?1)=1 .

2 控制器設計

在本節中,首先結合backstepping 方法和命令濾波技術,設計前饋控制器Ua.然后,采用自適應動態規劃方法設計出最優反饋控制器U?.最后,整個控制輸入Uw=Ua+U?.

2.1 前饋控制器設計

首先進行如下坐標變換

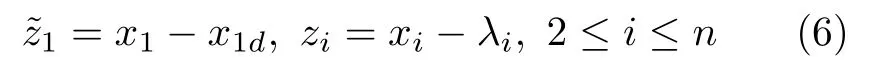
其中,x1d為參考信號,λi是虛擬控制輸入xid通過一階命令濾波器的輸出.是前饋虛擬控制輸入,為最優反饋虛擬控制輸入.最后一步中定義v=va+v?,va為前饋實際控制輸入,v?為最優反饋實際控制輸入.一階命令濾波器表達式為

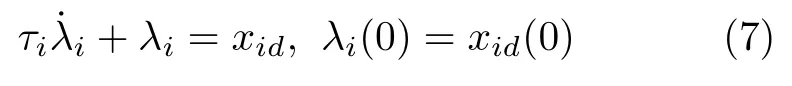
其中,τi是時間常數.為了消除濾波器誤差λi?xid的影響,設計誤差補償信號ζi(2≤i ≤n?1)為

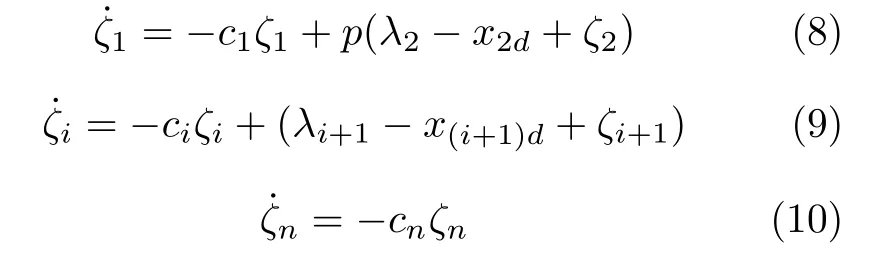
其中,ci >0是設計參數,ζ(0)=0 .

定義補償跟蹤誤差為

結合式(5)～(11),對求導可得

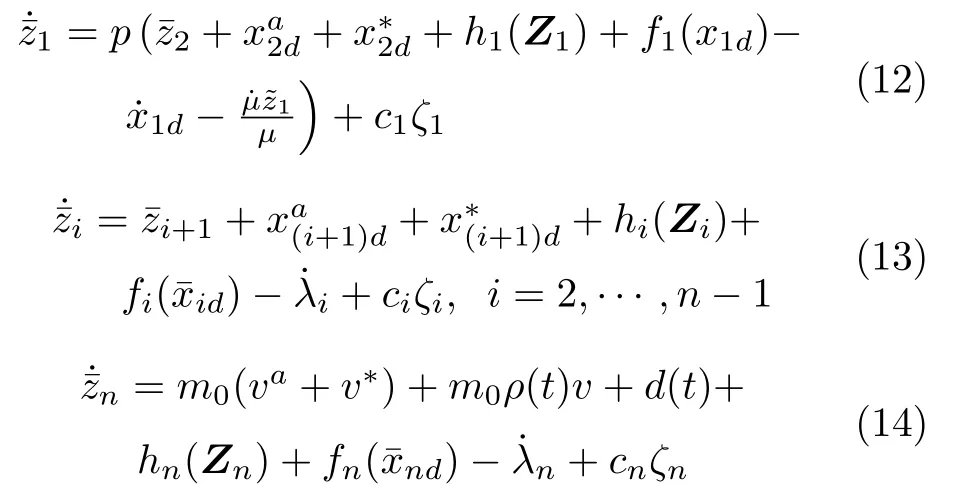
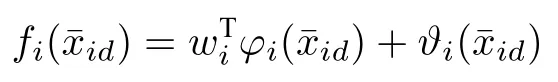
第1步:考慮如下Lyapunov 函數

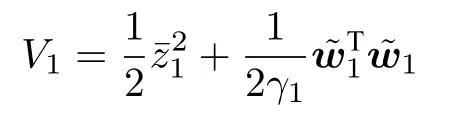
設計前饋虛擬控制器和自適應律如下:

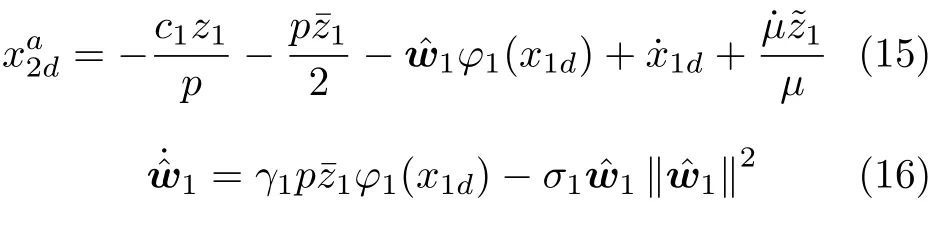
根據式(15)和式(16),對V1求導有

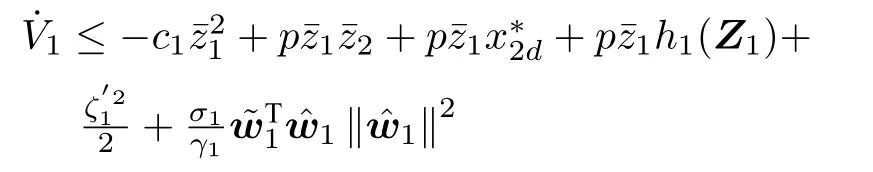
第i步(2≤i ≤n?1):考慮如下Lyapunov 函數

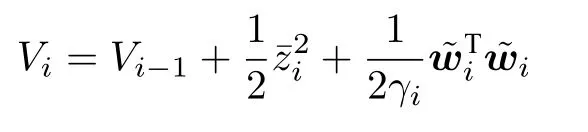
設計前饋虛擬控制器和自適應律如下:

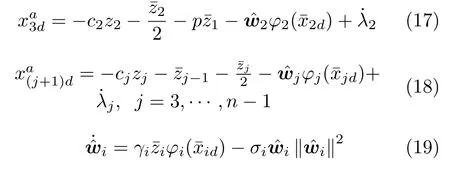
根據式(17)～(19),對Vi求導有

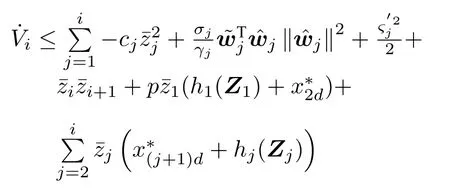
第n步:考慮如下Lyapunov 函數

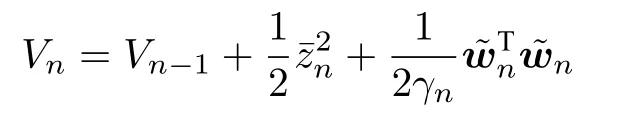
設計前饋控制器va和自適應律如下:

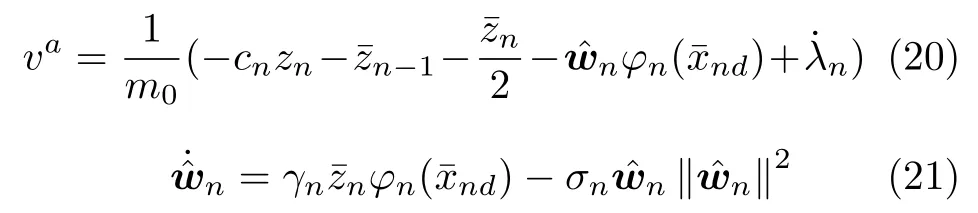
根據式(20)和式(21),對Vn求導有

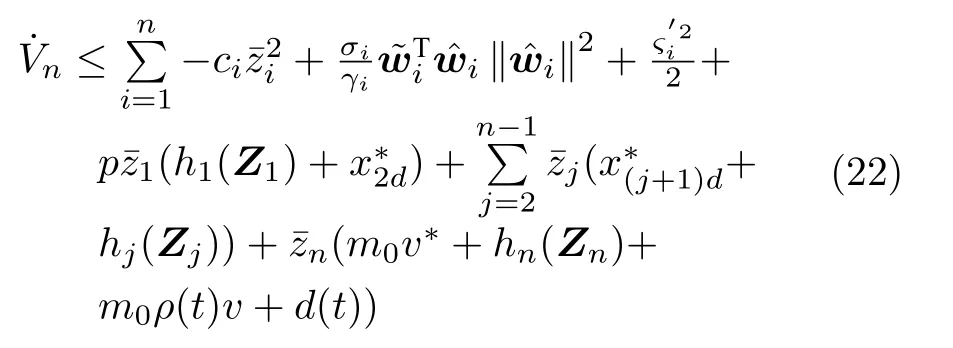
根據Young's 不等式,對式(22)不等式右邊第2、6 項變換如下

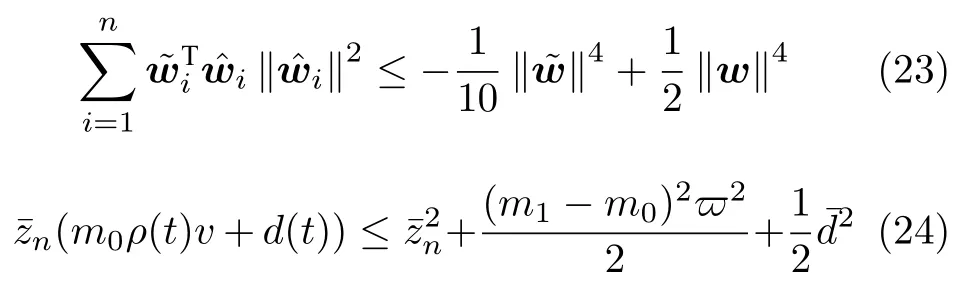
將式(23)和式(24)代入式(22),可得

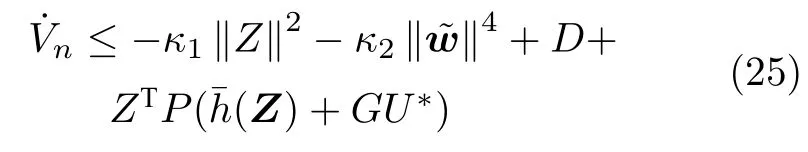
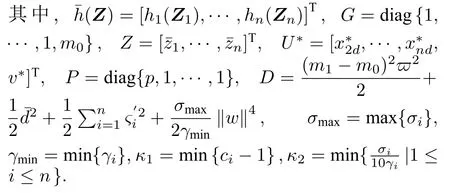
如前所述,系統(1)的控制輸入Uw=[x2d,...,xnd,v]T由兩部分Ua和U?構成,前饋控制器的表達式如式(15),(17),(18),(20)所示.由式(25)可知,前饋控制器Ua不能保證整個閉環系統的穩定性.因此,需要設計最優反饋控制器使得Uw能夠保證被控系統(1)穩定.

2.2 最優反饋控制器設計

本節中,設計最優反饋控制器U?使如下誤差仿射系統穩定,并且使得代價函數達到最小.

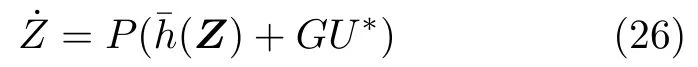
定義系統(26)的代價函數為

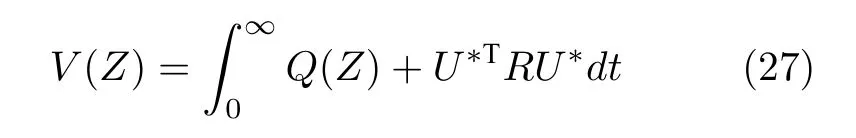
其中,Q(Z)是半正定的罰函數,R=RT>0 .

根據代價函數(27),定義哈密頓函數如下

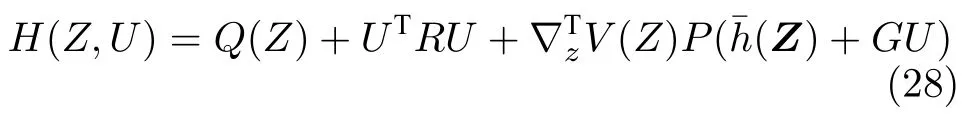
其中,?zV(Z)是V(Z)對Z的偏導,通過求解=0,解得最優控制輸入

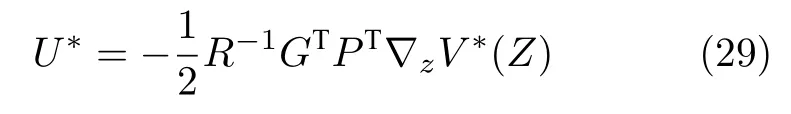
將式(29)代入式(28)可得最優控制輸入的充分必要條件:此時哈密頓函數最小.其中,E=PGR?1GTPT,且V?(0)=0.

引理3[27].對于系統(26),代價函數(27),最優控制器(29),存在徑向無界且連續可導的Lyapunov 函數J(Zs),J(Z),使得其中此外, Λ(Z)>0 是一個半正定函數矩陣,滿足當∥Z∥=0,有∥Λ(Z)∥=0;當?min≤∥Z∥≤?max,有Λmin≤∥Λ(Z)∥≤Λmax,?min,?max,Λmin,Λmax都是正常數; limZ→∞Λ(Z)=∞,同時使等式Q(Z)+U?TRU?=(Z)Λ(Z)成立,其中,那么可得

根據引理1,利用模糊邏輯系統逼近最優代價函數,可得

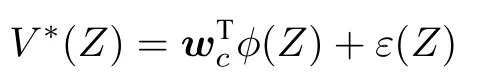
其中,wc為理想的權值,?(Z)為模糊基函數,ε(Z)為逼近誤差.則最優代價函數的梯度為

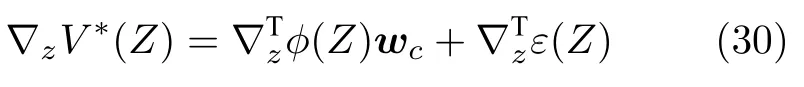
將式(30)分別代入式(28),(29)可得

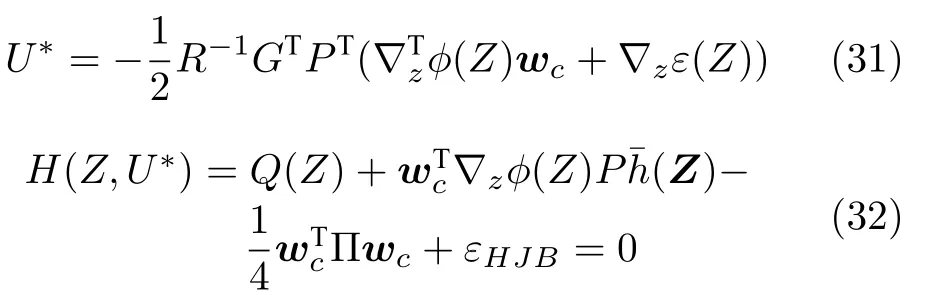
利用模糊邏輯系統對代價函數進行估計,則有

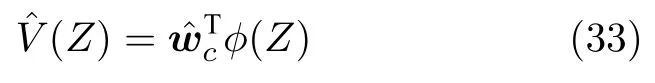
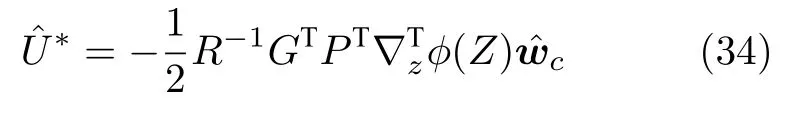
將式(34)代入式(28),得到哈密頓函數的估計為

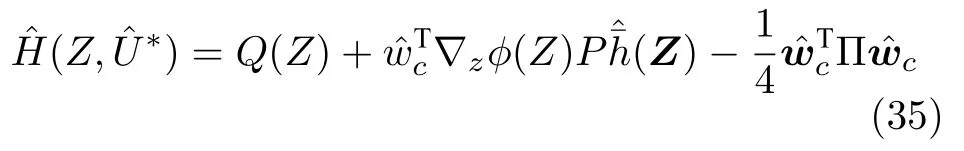
為使 最小,利用梯度下降法設計得

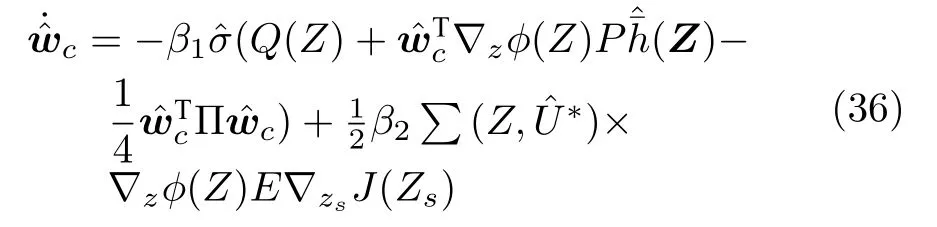
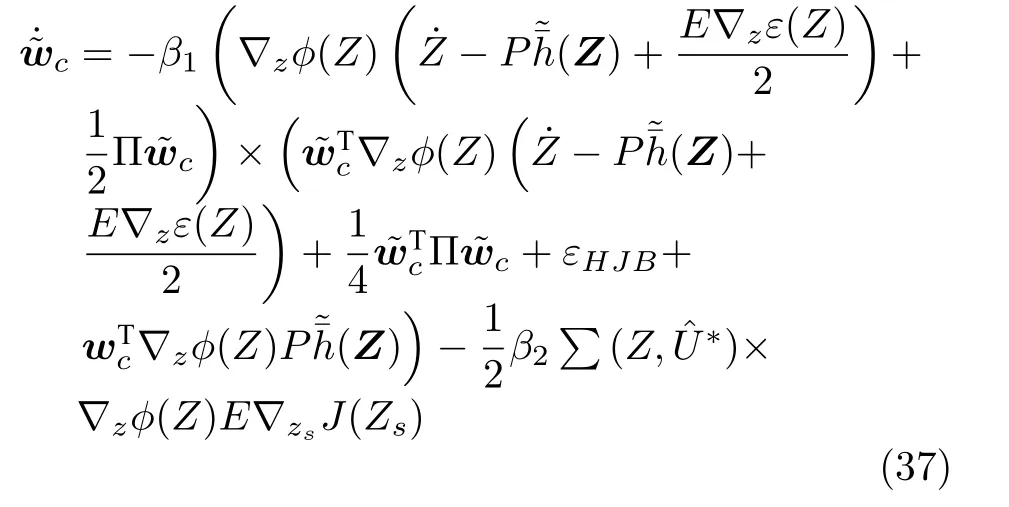
根據自適應律(16),(19),(21),引入附加項,可得

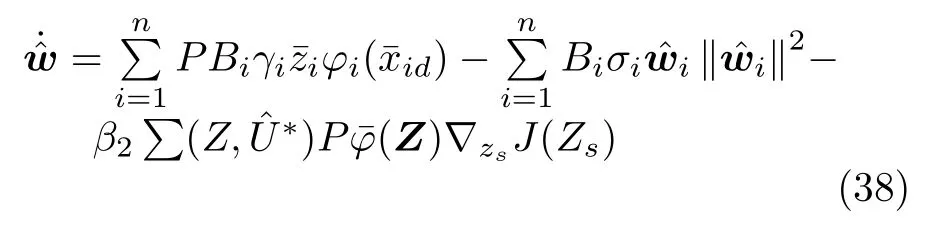
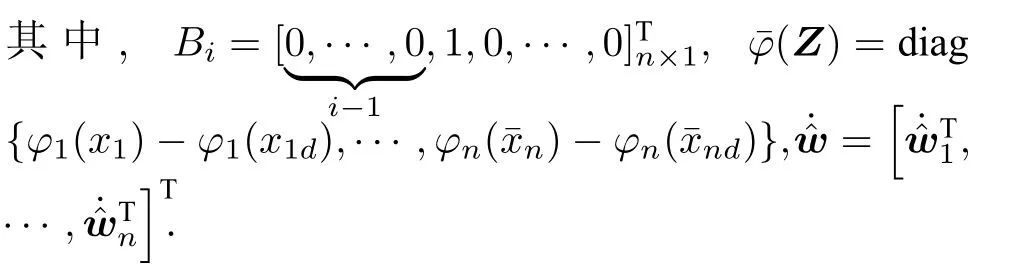
定理1.針對一類考慮指定性能和具有輸入死區約束的嚴格反饋非線性系統(1),設計前饋虛擬控制器(15),(17),(18),前饋實際控制器(20),反饋最優控制器(34)及自適應律(36)和(38),通過選擇合適的參數使得閉環系統內所有信號一致最終有界,跟蹤誤差以最優的方式收斂且滿足指定性能要求.

證明.見附錄A.

3 實例仿真

本節將通過一類機械臂系統仿真驗證所提出自適應模糊最優控制方法的有效性和可行性.帶有輸入死區約束的機械臂系統動力學方程如下:

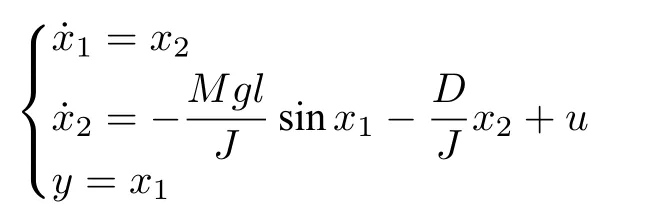
其中,x1,x2分別為連桿角速度和角加速度,M=1 kg為連桿總質量,g=9.8 m/s2為重力加速度,l=1 m 為機械臂連桿的質心距連桿的轉動中心的距離,D=2 N·m·s/rad 為連桿轉動的粘性摩擦系J=1 kg·m2數,為連桿轉動慣量.

參考信號x1d=sin(t).死區參數Mr=3,Ml=1,ar=1.5,al=3.模糊隸屬度函數為4,5.初始值為x1(0)=1.4 ,x2(0)=?0.2 .=[1,1,1,?1,?1]T.性能函數μ=2.5e?0.5t+0.05,δmin=0.6,δmax=0.8.設計參數為c1=10,c2=50,γ1=1,γ2=1,σ1=50 ,σ2=50 ,β1=0.01 ,β2=0.01,給定系統代價函數(27)中R=[0.2,0;0,0.01],其余參數初始值均為0.

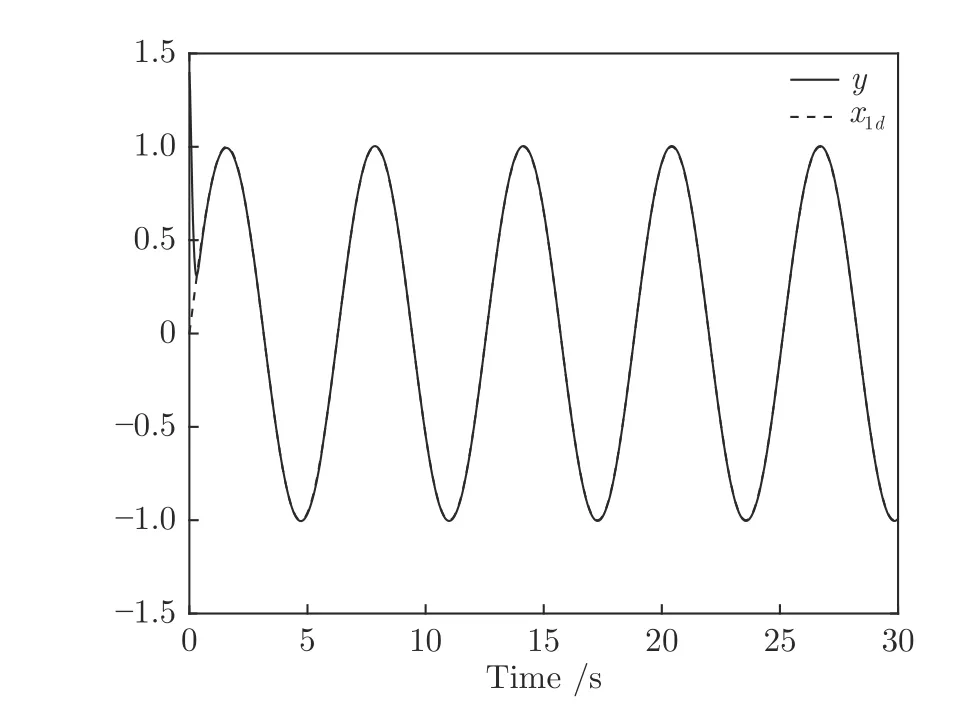
圖1 參考信號 x1d和輸出信號yFig.1 Reference signal x1d and output y

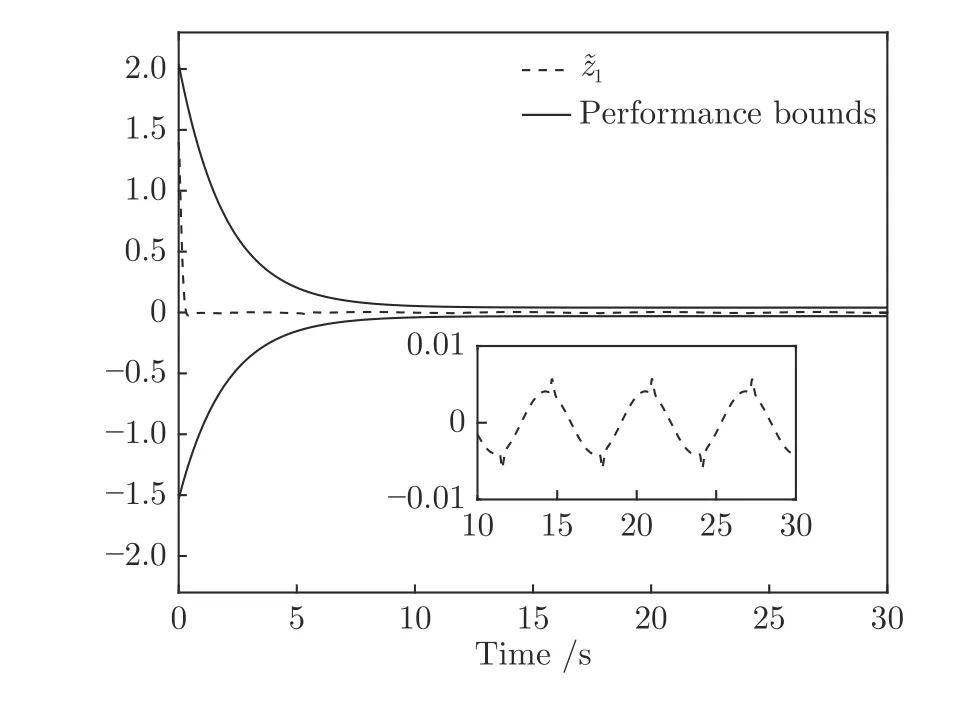
圖2 的軌跡和指定性能邊界曲線Fig.2 Trajectories of and performance bounds

仿真結果如圖1～4 所示,圖1 給出了參考信號x1d和系統輸出信號y的跟蹤軌跡,系統輸出y在5 s 內跟蹤上參考信號,表明本文的控制方法能使系統輸出具有良好的跟蹤效果.圖2 給出了跟蹤誤差的軌跡曲線,由圖中可以看出跟蹤誤差收斂于以原點為中心的有界鄰域內,滿足預設性能的要求,并且穩態誤差小于0.01.圖3 給出了代價函數權值和哈密頓函數的估計值的變化曲線,表明權值信號能快速收斂到目標權值并使得哈密頓函數趨于0.圖4 描繪了執行器輸入信號v和執行器輸出信號u的響應曲線.由仿真結果可知本文提出的控制方案使得閉環系統內所有信號都是有界的,保證了系統的穩定性.

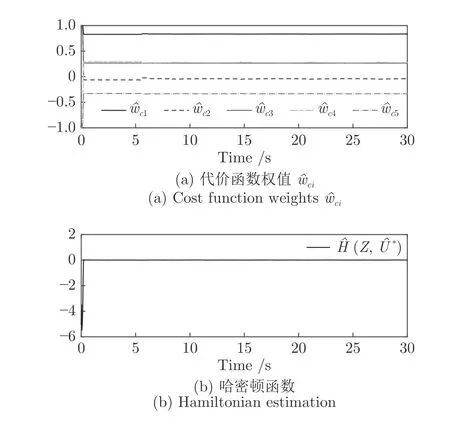
圖3 代價函數權值?和哈密頓函數?的軌跡(i=1,2,3,4,5)Fig.3 Thetrajectoriesof cost functions weights w?ci andHamiltonian ?(Z,?)(i=1,2,3,4,5)

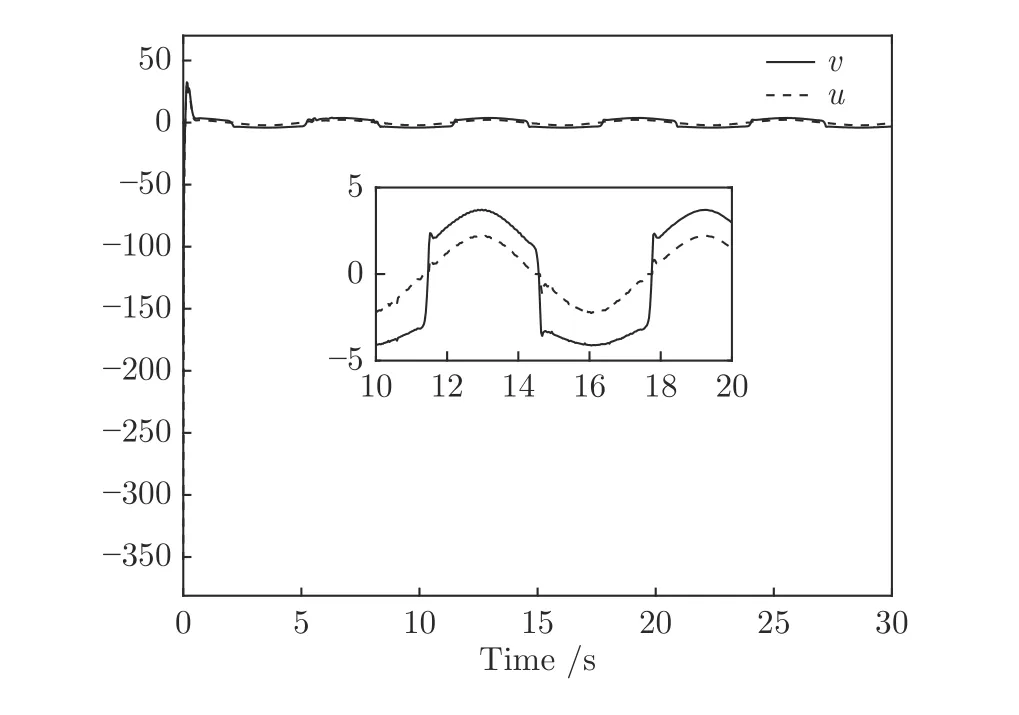
圖4 執行器輸入信號 v 和執行器輸出信號uFig.4 Trajectories of actuator input v and actuator output u

4 結束語

本文針對一類參數未知的嚴格反饋非線性系統,考慮輸入死區和指定性能兩個約束條件,提出了一種自適應模糊最優控制方法.首先在backstepping 方法和命令濾波技術的基礎上,利用死區斜率信息和性能指標函數設計了前饋控制器.進而采用單網絡的ADP 方法,設計了最優反饋控制器.最后采用Lyapunov 函數穩定性理論證明了閉環系統的穩定性.仿真結果表明了本文設計方法能夠有效解決考慮死區和指定性能的嚴格反饋系統的優化控制問題.

附錄A

選取Lyapunov 函數為