關注教學過程，注重思維訓練
——蘇科版《有理數乘方》教學設計

江蘇省常州市濱江中學 祁 敏

一、教材分析

《有理數的乘方》是蘇科版七年級上冊第二章第七節的知識點，是有理數的一項基本運算。學生現在已經學習了有理數加法、減法、乘法、除法這四項運算，而乘方是在前四項運算方法的基礎上產生的，不僅是對“有理數乘法與除法”的延續，還是下一節“有理數的混合運算”的基礎，具有承上啟下的作用。

二、學情分析

首先，從學生的認知特點進行分析：七年級學生具有較強的好奇心，尤其是對操作類的活動十分感興趣。所以，教師在實際教學中要給學生創設一個良好的探究情境，讓學生自己尋找和發現運算規律，并且讓學生自己歸納，在提高學生歸納能力的同時感受數學符號的美。

其次，從知識基礎進行分析：學生在小學就已經學過正數的平方和立方，這樣對乘方也就有較好的理解。另外，上節課知識點就是有理數的乘法與除法，學生對其運算法則有準確掌握，這樣在理解有理數乘方運算法則的時候就更加輕松。

三、教學目標

1.知識與技能目標：學生對有理數的冪、指數、底數、乘方的概念有準確理解，并掌握有理數乘方的計算方法。

2.過程與方法目標：在推導有理數乘方的過程中，讓學生感受乘方與乘法兩者之間的聯系與不同；在乘方運算中，觀察冪的變化并探索其規律，感受冪的運算變化。

3.情感態度目標：對學生的總結能力進行培養，同時讓學生對生活中存在的有理數乘方進行探究，提高學生的學習興趣。

四、教學重難點

難點：正確理解乘方的概念與意義，并掌握有理數乘方的計算方法，學會運算。

重點：掌握有理數乘方與冪之間的意義、區別，找到冪的符號規律。

五、教學過程

板塊一：創設情境，導入課題

教師先通過多媒體給學生創設一個情境：全球海拔最高的山峰就是珠穆朗瑪峰，高度為8844 米，但是你們知道嗎？一張厚度為0.1毫米的紙在經過幾十次的對折以后，將其厚度累計起來要大于珠穆朗瑪峰的高度，但是前提條件是紙張面積足夠大。如果紙張的面積更大，堆積的高度可以是地球到月球的距離，你們相信嗎？

學生A：我不相信，這不可能。

學生B：這是不可能的，地球到月球的距離大約是384401 千米，紙張怎么可能折得那么厚。

學生C：我覺得有可能，因為數學具有無窮的奧秘。

教師：你們有的認為不可能，有的認為可能，那么我們用數學思維與科學手段驗證一下這個可能性。（板書“有理數的乘方”）

【評析】眾所周知，思考開始于疑問。利用學生都熟悉和知道的事物創設教學情境，并設置疑問，可以將學生的好奇心與求知欲充分激發出來。

板塊二：合作交流，探求新知

教師：下面我們拿出一張紙，先對折一次，然后再對折……一直對折下去，并思考回答相關問題：第一次對折紙張有幾層？第二次對折紙張有幾層？第三次對折紙張有幾層？……第三十次對折紙張有幾層？……第一百次對折紙張有幾層？

以小組為單位開展活動，每個小組兩人，一個人記錄，另一個人操作，一分鐘以后看你們的成果。

某小組的成果展示：第一次對折紙張層數（2），第二次對折紙張層數（2×2），第三次對折紙張層數（2×2×2）。

教師：那你們可以說說紙張對折三十次的層數嗎？一百次呢？

教師：請你們仔細觀察這些式子，想一想，這些算式是哪種數學運算？有哪些特點？

學生B：都是乘法運算，特點就是所有算式的因數相同。

教師：你們可以將這些算式用最簡單的式子進行表示嗎？

【評析】在本次動手操作活動中，學生的探究興趣被充分激發出來，思維也逐漸隨著教師的腳步深入。

教師：我們在小學的時候就學過，如果計算正方體的體積以及正方形的面積，如正方體和正方形的邊長都是5，那你們說說正方體的體積以及正方形的面積。

學生A：正方體的體積是5×5×5，化簡為53；正方形的面積是5×5，化簡為52。

教師：它們怎么讀？

學生B：53讀5 的立方；52讀5 的平方。

教師：在記法中，5 是如何確定的？右上角標的數是如何確定的？

學生C：5 是正方體與正方形的邊長，是相同的因數，角標是因數的個數。

教師：請你們根據這種記法和讀法，對剛才活動中得到的式子進行讀與記。

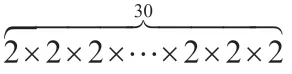
教師：那你們可以用乘方將n個a相乘表示出來嗎？

【評析】通過該教學板塊的設計，學生在探索與交流中更好地發現冪的規律，并且參與教學活動的意識也更強，教學活動的質量也更高。

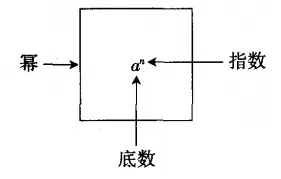
【板書】乘方就是求多個相同因數的積的運算；因數角標為指數；乘方結果為冪；讀作a的n次方或者a的n次冪。意義就是表示n個a相乘。

板塊三：基礎訓練，理解新知

練一練：

①4×4×4 的乘方形式______。

③（-5）3的意義是______。

六、布置作業

在課下找找日常生活中存在的有理數乘方的例子，下節課進行分享與交流。

七、教學反思

本節課的教學效果還較為可觀，但是有個別方面還需要完善，如在板塊二引入正方體與正方形的過程中，不應該直接給出數字，而應該用不同字母表示；對于特殊的冪（單獨的一個字母或者一個數），需要講解一下。