交通結構優化下的城市停車需求預測研究

劉 怡，常玉林,2,張 鵬

(1.江蘇大學 汽車與交通工程學院， 江蘇 鎮江 212013； 2.東南大學 城市智能交通江蘇省重點實驗室， 南京 211189)

隨著汽車保有量的不斷增加，城市“停車難”的問題日益嚴峻，繼而引發的交通問題日益顯著，已經成為制約城市可持續發展和影響人們生活質量的焦點問題。為了合理規劃停車場，準確預測城市停車泊位需求是做好停車規劃的前提與關鍵。

目前常用的停車需求預測模型主要有用地分析預測、機動車OD預測、交通量-停車需求預測、相關分析預測等方法[1-2]，也有部分學者考慮停車需求的影響因素提出了一些修正預測模型[3-4]。以往的研究很少將政府決策者對城市交通結構的引導作用考慮進去。對于出行者而言，在選擇交通方式時一般會優先考慮出行方式的經濟、時間效用。但對于政府決策者而言，各種出行結構帶來的交通、環境影響不容忽視。在城市交通系統對生態環境的影響越來越嚴重的背景下，通過優化城市交通結構實現節約不可再生資源、減少環境和交通影響勢在必行[5-6]。

合理地引導城市交通結構能使機動車的出行維持在一個合理的比例，從而減小城市停車需求，緩解“停車難”問題。基于以上分析，筆者通過優化城市交通結構，得到城市交通結構優化下的城市停車需求預測模型。

1 停車需求預測模型建立

城市停車泊位需求一般由基本停產需求和彈性停車需求組成，故停車泊位需求為基本停車泊位需求與出行泊位需求的總和。城市停車泊位需求總量V可表示為

V=V1+V2=P×(1+R)

(1)

式中：V1為基本停車泊位需求；V2為彈性停車泊位需求；P為城市規劃年機動車保有量；R為彈性需求影響系數。

文獻[7]在考慮停車彈性需求影響因素時，根據影響因素與停車需求的正比或者反比關系，提出了停車彈性需求修正模型，其中彈性需求系數R可表示為

(2)

式中：r1為機動車出行率；r2為停車供應區域差別化調控系數；r3為泊位共享能力；t為停車泊位周轉率；s為停車泊位利用率。對于模型中彈性需求系數，可通過對城市的交通特征和政策導向分析得到。

從式(2)可以看出，停車需求雖然有很多因素影響，但是機動車保有量作為模型中的關鍵變量，直接影響到城市停車需求的總量。

2 規劃年機動車保有量預測

2.1 機動車保有量的數學分析方法

國內的機動車保有量預測方法主要可以分為外推法預測、因果法預測和判斷分析法預測[8]，單一的預測模型往往無法保證模型的精確程度。綜合比較這3類方法，選用灰色預測模型GM和指數平滑模型組合預測方法進行預測。灰色預測模型GM和指數平滑模型的具體步驟可以參考文獻[8]。組合預測方法可以綜合利用各單項預測方法提供的有效信息來提高模型預測精度[9]。

假設f1、f2分別對應2種方法規劃年機動車保有量的預測值，e1、e2分別為灰色預測模型GM和指數平滑模型的預測誤差，w1、w2為對應的組合系數，且w1+w2=1，故

fc=w1f1+w2f2

(3)

使用方差-協方差法組合預測方法，則誤差ec及方差var(ec)分別為

ec=w1e1+w2e2

(4)

(5)

關于w1，對var(ec)求極小值可得

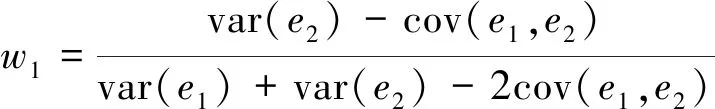
(6)

由于GM和指數平滑模型的建模方法、思路以及步驟都截然不同，可以把這兩種預測方法看作是相互獨立的預測模型，則有cov(e1,e2)=0，令var(e1)=δ1，var(e2)=δ2，可得：

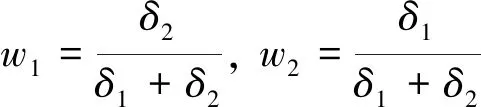
(7)

2.2 基于交通結構優化的機動車保有量

1) 建立交通結構優化的目標函數

合理地優化城市交通結構，在城市交通系統各種約束條件下，通過對各種交通方式發展的合理引導下，使之在能最大化滿足城市交通效率的同時，達到對環境影響最小。基于以上分析，兼顧城市交通效率和環境影響，建立的交通結構優化模型為：

(8)

(9)

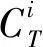
式(8)為模型的第1個目標函數，體現交通系統的效率最大化；式(9)為模型的第2個目標函數，體現交通系統對城市環境影響的最小化。

2) 約束條件分析

城市交通系統持續穩定的發展受到城市經濟、人口、資源和環境等多方面的制約影響[10]。建立的約束條件①～⑥依次為客運周轉量約束、出行可達性約束、城市交通發展規模約束、客運量約束、能源消耗約束和道路資源約束，約束條件整理得：

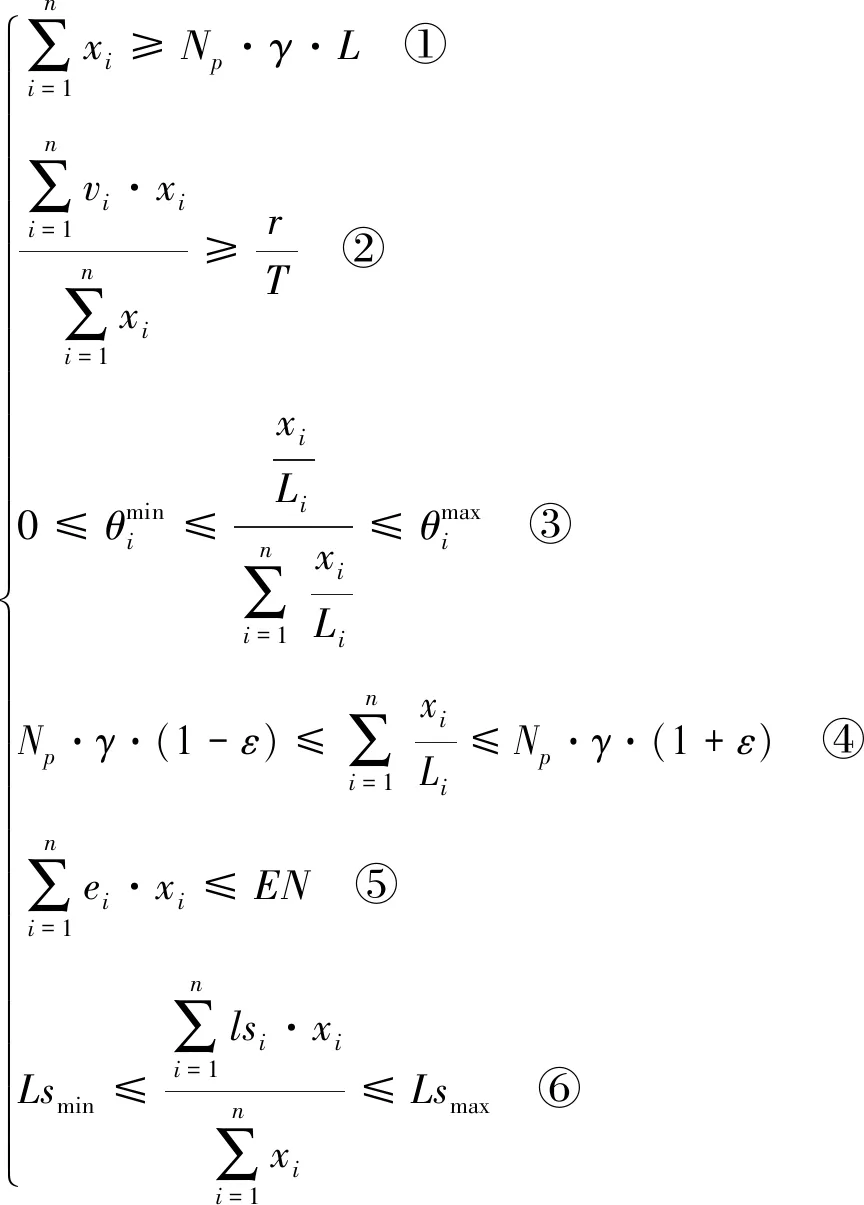
(10)

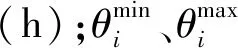
約束①保證了在各種交通方式組合下能保證城市居民的出行總量要求；約束②保證了城市居民能夠在合理的預算時間內到達城市的目的地；約束③保證城市交通發展規模應在城市交通規劃的范圍內；約束⑤保證了各種交通方式所承擔的客運周轉量與該種交通方式的居民平均出行距離的比例關系應與城市居民的出行總量大致相等[10]；約束⑥保證了城市人均占地面積應在一定范圍內。

對于居民出行總量約束④中規劃年第i種交通方式承擔的平均出行距離Li，計算公式為：

(11)

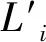
對于能源消耗約束⑤中允許城市客運交通系統承擔的能耗限值EN，計算公式為

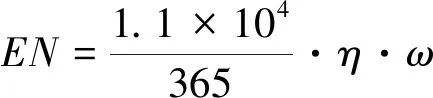
(12)

式中：η為城市能源利用率；ω為城市規劃人口。

機動車的保有量與機動車在城市交通系統中承擔的客運周轉量xcar有關，可以通過城市居民中選擇機動車出行的人數除以汽車人均載客數ncar得到，具體可計算為

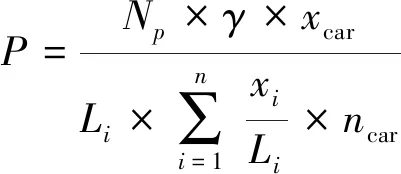
(13)

3) 模型的求解

上述優化模型為典型的多目標決策問題，考慮采用理想點法對模型進行求解。

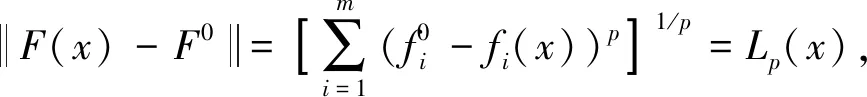
步驟3求解最優近似解x*。

3 實例分析

以常州市金壇市為例，利用建立的模型對交通結構優化下的停車需求進行預測。以2015年為基礎年，2020年為目標年。根據金壇市現階段的發展情況，將金壇市的交通結構分為步行、非機動車、常規公交、機動車、出租車和摩托車5種類型。根據金壇市城市規劃中的內容[11]，金壇區現階段城市用地面積39.74 km2，規劃到2020年城市用地面積40 km2，城市等效半徑為3.5 km，居民出行平均預算時間為40 min，規劃年居民平均出行距離為4 km，平均出行次數為2.7次/日，規劃2020年城市人口為65萬人，2020年總能耗限值為12.05 MJ/人·日，允許城市客運交通系統承擔的能耗限值為7.8×106MJ，規劃城市人均占用道路面積的下限和上限分別為6 m2/人和13.5 m2/人，2011—2015年金壇市中心城區的機動車保有量分別為3.091 8萬輛、3.86萬輛、4.704萬輛、5.653 1萬輛和6.769 8萬輛。

3.1 機動車保有量預測

灰色預測模型與3次平滑指數模型對機動車保有量預測的結果見表1，對應的誤差值見表2。

表1 2016—2020年預測的機動車保有量

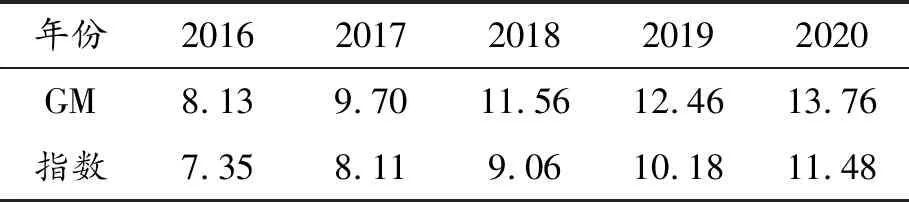
年份20162017201820192020GM 8.139.7011.5612.4613.76指數7.358.119.0610.1811.48

表2 GM模型誤差與指數平滑誤差值

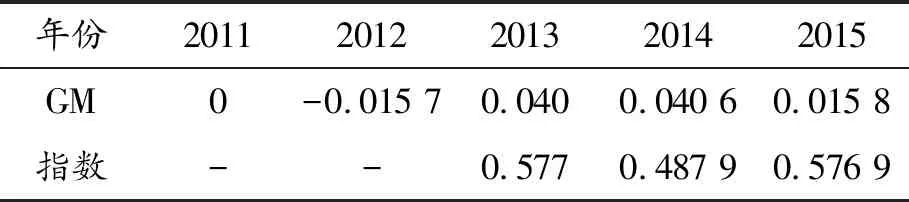
年份20112012201320142015GM 0-0.015 70.0400.040 60.015 8指數--0.5770.487 90.576 9

采用方差-協方差對機動車保有量組合預測，求得：w1=0.97，w2=0.03，故組合預測模型為：f=0.97f1+0.03f2，最終的機動車保有量預測值如圖1所示。從圖1中可以看出，2011—2020年機動車增長較為平緩，預測的機動車增長趨勢與歷年的增長趨勢較為一致，說明GM-指數平滑組合模型預測的結果較為合理。2020年金壇市中心城區機動車保有量預測值為13.6萬輛。

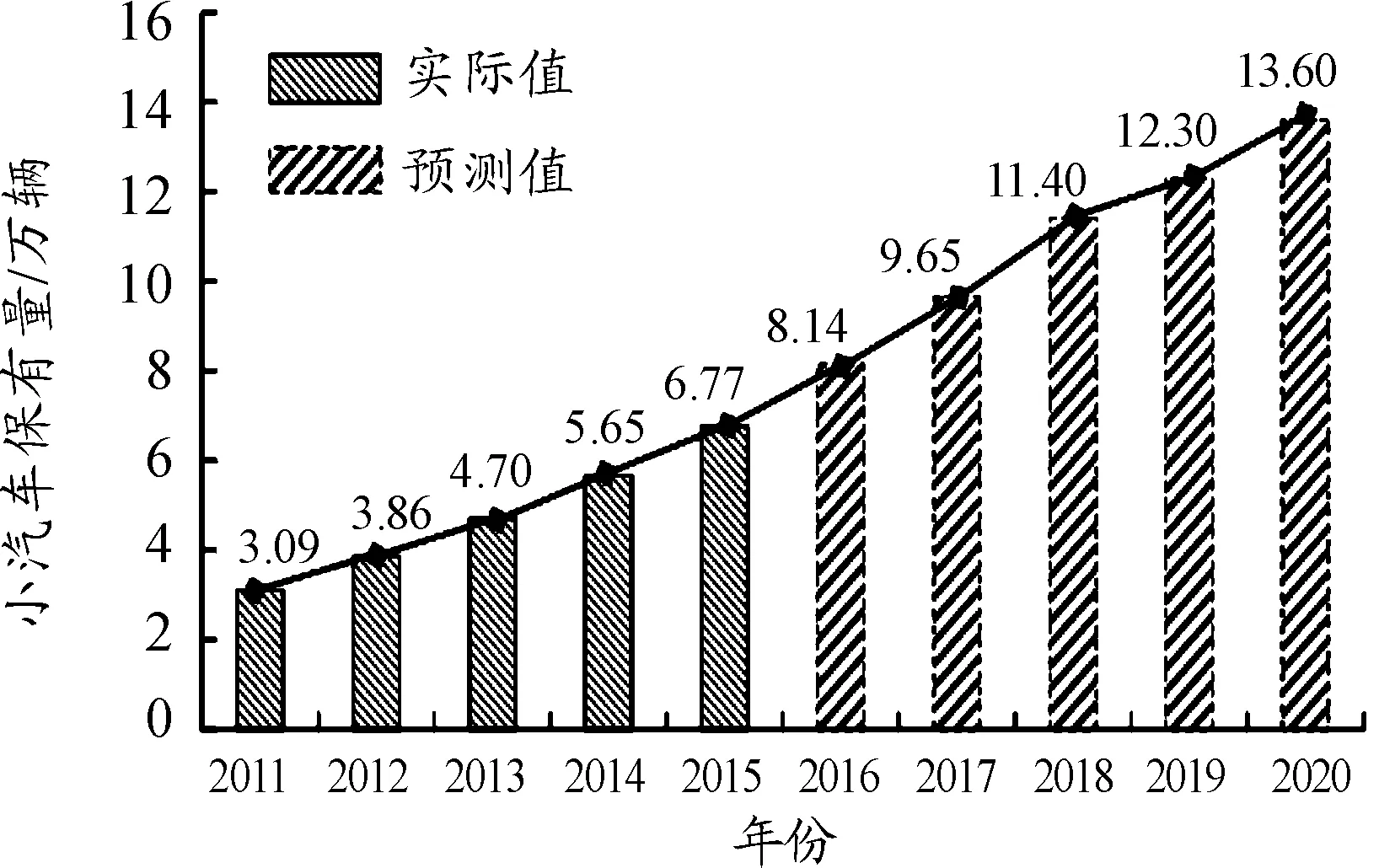
圖1 機動車保有量增長趨勢圖

3.2 交通結構優化

筆者分析了部分規模與金壇市相近的城市，對應的城市交通結構見表3，將表中各種交通方式的分擔率繪制在圖2中，可以發現中小城市的交通結構集中在慢行交通導向的模式。結合金壇市實際發展情況，金壇市2020年的交通結構發展趨勢為慢行交通導向的發展趨勢。參照文獻[10,12-13]，確定各交通方式的相關參數，見表4。

表3 部分城市各交通方式在交通結構中的分擔率

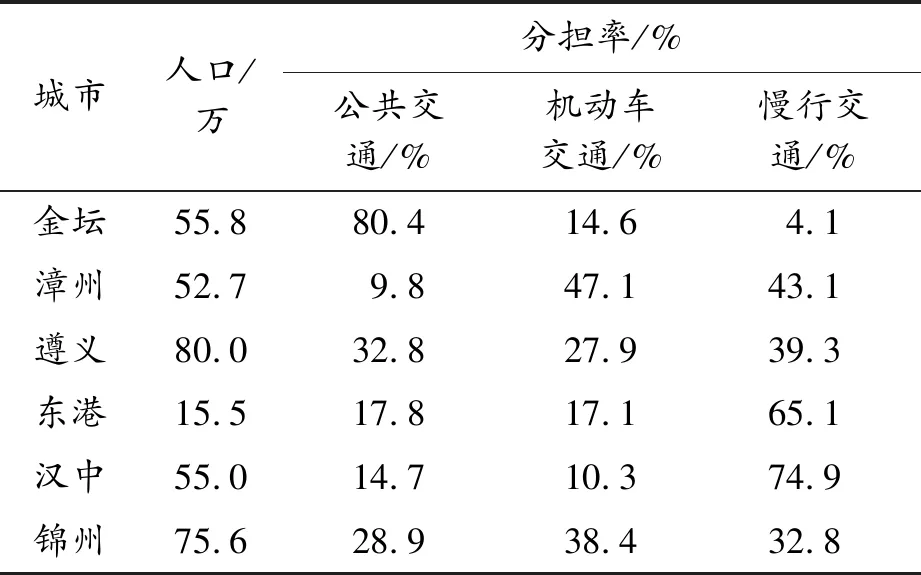
城市人口/萬分擔率/%公共交通/%機動車交通/%慢行交通/%金壇55.880.414.64.1漳州52.79.847.143.1遵義80.032.827.939.3東港15.517.817.165.1漢中55.014.710.374.9錦州75.628.938.432.8

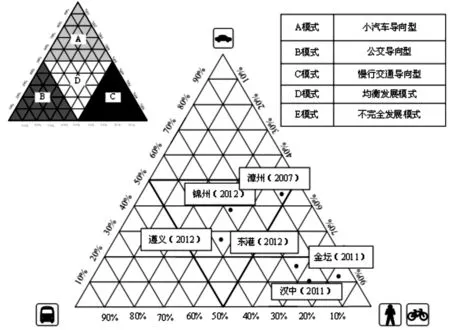
圖2 部分城市的交通結構發展模式

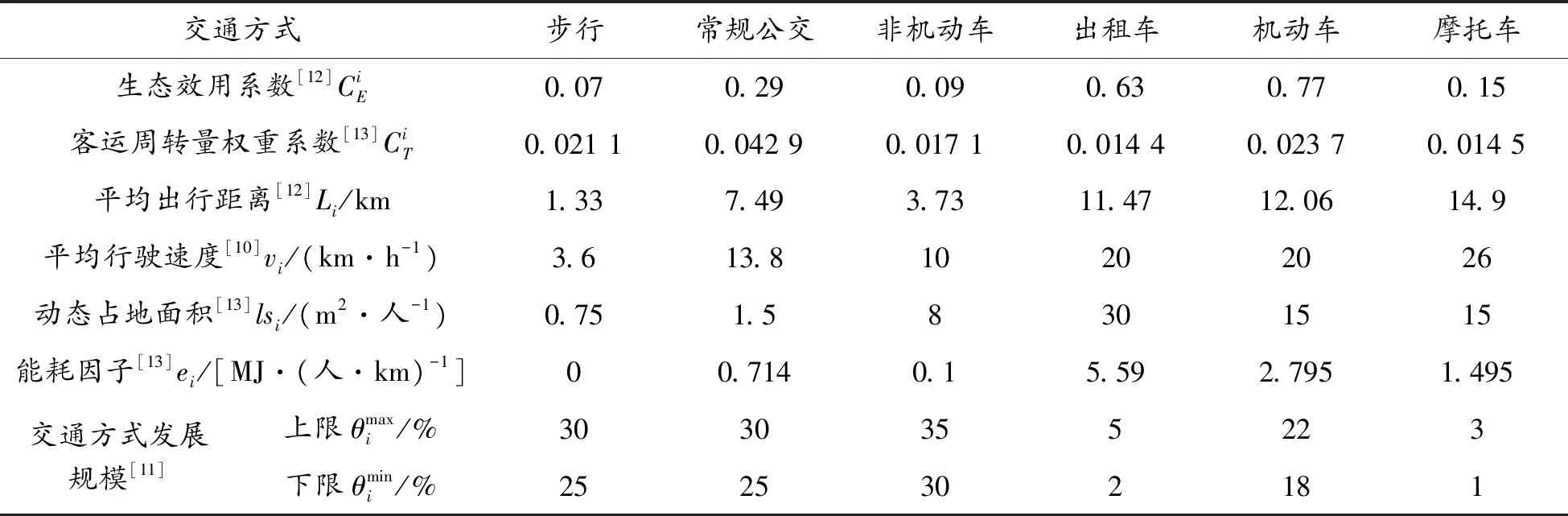
表4 模型中的相關參數

將相關參數代入交通結構優化模型，借助lingo軟件求解，對單目標求出最優解，分別為x(1)=(49.02,400.26,206.20,42.27,400.02,27.46),x(2)=(53.22,312.19,186.57,38.25,361.93,24.84),對應的目標值分別為32.22，417.56。構建函數

(14)

求解過程如圖3所示，最優解x*=(49.23,312.19,197.74,38.25,361.93,24.84)。求得各種交通方式的分擔率見表5。可以得到金壇市2020年機動車的分擔率為20%。

規劃年金壇市中心城區人口總數為35萬人，機動車人均載客數取1.41人/車，則可計算的金壇市中心城區的機動車保有量P為13.4萬輛，與傳統的數學分析方法相比，機動車的保有量減少了0.2萬輛，結果更為準確，數據的依據性更強。

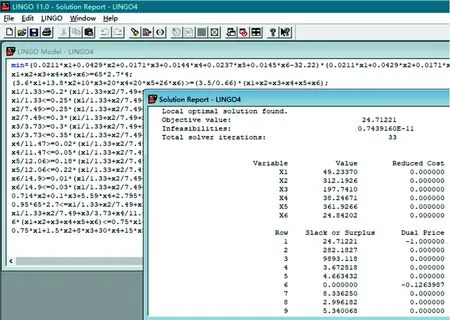
圖3 lingo求解過程

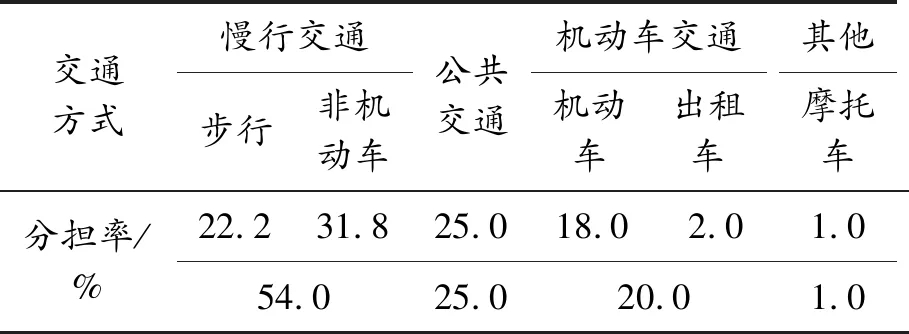
表5 各種交通方式的出行分擔率

3.3 中心城區停車需求總量預測

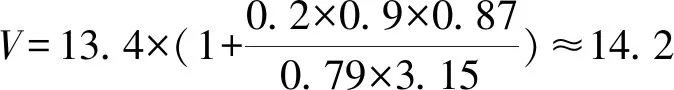
4 結束語

城市的停車需求主要由機動車的保有量決定。建立城市的停車需求預測模型，對模型中的機動車保有量分別基于傳統的數學分析方法和交通結構優化方法建立了預測模型。其中數學分析方法是以灰色模型與平滑指數模型相結合的組合預測的方法預測得到未來年機動車保有量；交通結構優化模型是以城市交通效率最大和環境影響最小為目標函數，并以客運周轉量、出行可達性、城市交通發展規模、客運量、能源消耗和道路資源為約束條件，得到機動車在城市交通系統的分擔率。最后以金壇市為例，對中心城區規劃年的停車需求進行預測，結果表明：與傳統的數學分析方法相比，交通結構優化模型得到的機動車保有量減少了0.2萬輛，城市停車需求為14.2萬個，結果更為準確，數據的依據性更強。