關于(a,b,0)分布類的特征函數統一表達式的若干標記

李 浩，劉 莉，李 杰，屠瑤瑤，翟文祥

在非壽險精算理論中，為了刻畫保單的索賠次數分布，需要建立索賠次數模型［1-4］.常用于刻畫索賠次數的分布有泊松分布、二項分布、幾何分布和負二項分布，四者可以統一表示為一種分布類，稱為 (a,b,0)分布類［5-8］.此分布類在非壽險精算的實務中應用較為廣泛，尤其是在非壽險產品定價中會起到很重要的作用，其中會涉及到該分布類的特征函數、矩母函數和概率生成函數等.文獻［1-2］給出了(a,b,0)分布類的矩母函數和概率生成函數統一表達式的結論.

矩母函數和概率生成函數的被積函數都是一個實值函數，積分有時未必存在，從而兩者對一切實數未必都有定義.因此，并不是所有的分布函數都有矩母函數和概率生成函數與之對應.而特征函數是一個實變量的復值函數，對一切實數都有定義，并且隨機變量的特征函數可以通過傅里葉積分變換與分布函數建立一一對應的關系.所以探討(a,b,0)分布類的特征函數具有一定的理論意義.

1 基本定義

定義1［3］設隨機變量N的分布列{ }pk滿足

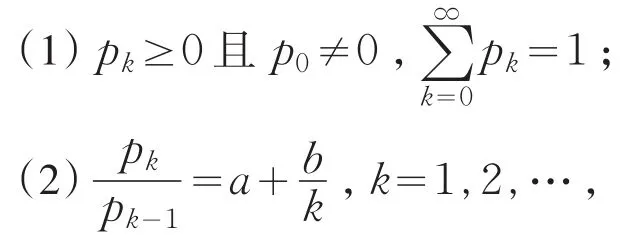
則稱N的分布為(a,b,0)分布類，其中a和b為參數.

定義2［3］設隨機變量X的分布函數為F(x)，其特征函數定義為

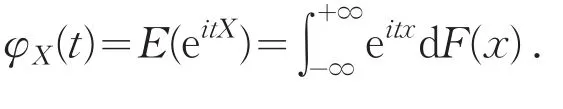
2 主要結果

定理1(a,b,0)分布類的一階原點矩與二階中心矩具有統一表達式，可表示為k=1,2.

證明 設隨機變量X服從(a,b,0)分布類，根據(a,b,0)分布類的定義，可以分別求出其期望及方差.由(a,b,0)分布類的定義可知，對于取值為非負整值隨機變量N，其期望為

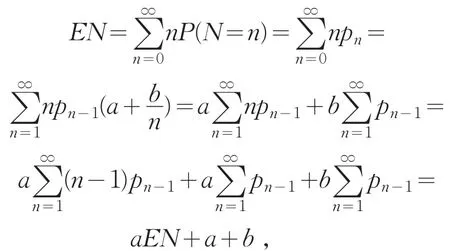
由(a,b,0)分布類的定義可知，對于取值為非負整值隨機變量N，其方差為

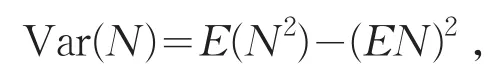
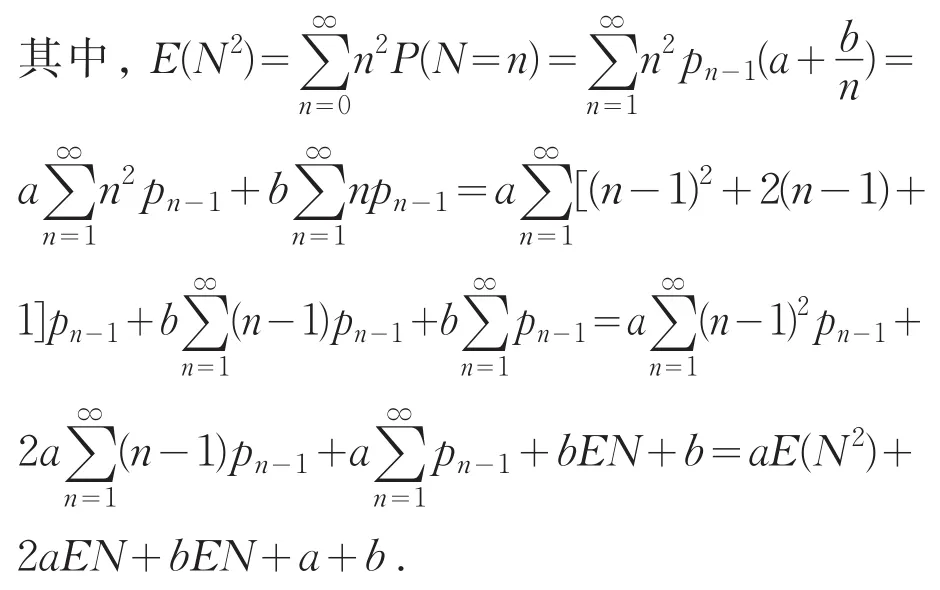
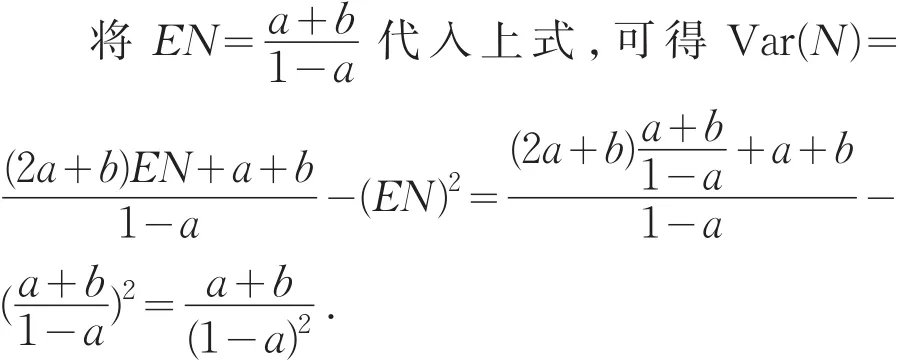
定理2(a,b,0)分布類的矩母函數可用參數a和b表示為統一表達式，即

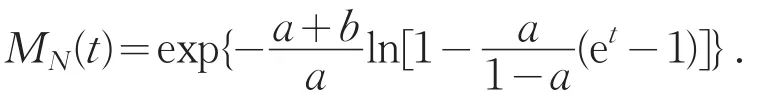
定理3(a,b,0)分布類的概率生成函數可用參數a和b表示為統一表達式，即

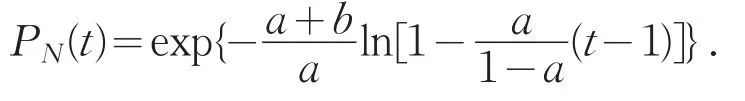
從特征函數、矩母函數和概率生成函數的定義出發，可以得到三者之間的關系為

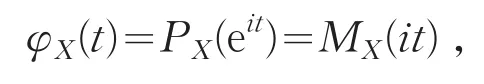
其中，MX(t)、PX(t)分別為隨機變量X的矩母函數和概率生成函數.

定理4(a,b,0)分布類的特征函數可用參數a和b表示為統一表達式，即

對應于式(3)，用于方位向成像的指數項為第二項.此時將其他項并入幅度可得到同式(4)的N組方位向重構模型為

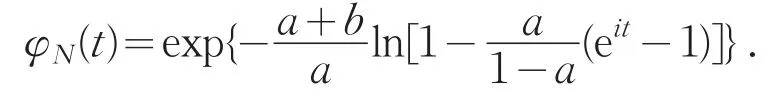
證明 由特征函數與矩母函數及概率生成函數的關系，可將矩母函數MX(t)中的變量t替換為it，或者將概率生成函數PX(t)中的變量t替換為eit，即可得特征函數對應的表達式.

推論1泊松分布的特征函數為φN(t)=exp(λ(eit-1)).

證明 當a=0，b=λ時，(a,b,0)分布類即為泊松分布.結合結論3.2［1］的證明方法，以及矩母函數與特征函數的轉化關系，即可得泊松分布的特征函數表達式.

推論2二項分布的特征函數為φN(t)=exp{mln[1+q(eit-1)]}.

推論3負幾何分布的特征函數為φN(t)=exp{-rln[1-β(eit-1)]}.

推論4幾何分布的特征函數為φN(t)=

(a,b,0)分布類中的四個分布的特征函數表達式，如表1所示.

表1 (a,b,0)分布類的特征函數

注：①當r=1時，負二項分布即為幾何分布，則幾何分布的特征函數便可由負二項分布的特征函數得到；

②令二項分布中的兩參數m=-r，q=-β，二項分布即為負二項分布，則二項分布的特征函數亦可由負二項分布的特征函數得到；

③由泊松逼近定理可知，在滿足一定條件下，泊松分布可以看成是二項分布的極限形式.因此泊松分布的特征函數表達式，完全可以由二項分布與負二項分布的特征函數表達式給出.

3 結論

在精算模型中，刻畫保險的理賠次數的分布，是一個重要的理論問題.由于理賠次數是離散型隨機變量，所以使用概率理論中用于刻畫離散型隨機變量分布的幾種重要分布，如泊松分布、二項分布、負二項分布及幾何分布.以上四種分布存在一定的內在聯系，將它們的分布類統一起來，得到了(a,b,0)分布類這一概念，于是常用(a,b,0)分布類及(a,b,1)分布類以描述保險的理賠次數的分布情況.非壽險產品在價格厘定過程中，產品的定價模型需要考慮利率、理賠額及理賠次數等因素，定價模型的計算會涉及到矩母函數、概率生成函數及特征函數.因此建立(a,b,0)分布類的矩母函數、概率生成函數及特征函數的表達式及三者之間的關系尤為重要，而三者中唯有特征函數與分布函數具有一一對應的關系，所以本文正是在文獻［1-2］的基礎上，受啟發得出(a,b,0)分布類中各分布的特征函數具有統一表達式的結論.在刻畫非壽險產品索賠次數分布這一類問題時，常用二項分布或者負二項分布等，但是它們不一定都存在矩母函數，這樣就不能完全利用分布的矩母函數進行定價，而特征函數克服了以上缺點.因此，在非壽險產品定價時，可以考慮先確定特征函數，再利用特征函數與矩母函數之間的關系，進一步建立定價模型.