基于信息熵抽樣估計的統計學習查詢策略

曲豫賓，陳 翔

傳統有監督學習是使用標記數據集訓練模型，然而標記數據集有時候需要花費大量時間與成本，主動學習［1］框架通過在未標注數據集中選擇少量示例進行標注，達到較好的分類效果.基于池的主動學習查詢策略大致可以劃分為基于異構標準的樣例選擇策略、基于性能的樣例選擇策略、混合選擇策略等［2］.基于異構標準的樣例選擇策略包括Uncertainty Sampling，Query-By-Committee，Expected Model Change［1］等；基于性能的樣例選擇策略包括ExpectedErrorReduction，Variance Reduction；混合選擇策略包括Density-Weighted Methods，QUIRE等幾種.常見用于分類的模型包括樸素貝葉斯、隨機森林、支持向量機等.

本文重點關注基于統計學習的主動學習查詢策略，該類策略是從影響主動學習的分類性能出發選擇標注樣例.同時關注基于信息異構的主動學習查詢策略.

Uncertainty Sampling基于不確定度的角度來選擇未標注樣例，實踐中發現該策略具有較強的魯棒性，但是存在異常點選擇的問題；Query-By-Committee維護分類器集合，根據不同分類器的不一致性作為選擇未標注樣例的標準，常見的評價標準包括VoteEntropy，Killback-Leibler divergence［1］等，該策略本質上是一種通過對假設空間的收縮來實現樣例選擇；Expected Model Change策略使用決策信息論的方法選擇對模型影響最大的未標注實例；Expected Error Reduction是基于統計學習理論直接計算未標注樣例的不同標注帶來的期望風險，根據期望風險最小化準則來選擇未標注樣例，該策略優點是根據樣例直接計算優化損失函數，但存在計算復雜度較高的問題；Variance Reduction策略不是通過直接優化期望風險，而是間接地減少輸出方差實現對未標注樣例選擇；Density-Weighted Methods在考慮未標注樣例信息量的同時考慮未標注樣例的代表性，對信息量與代表性施以不同的權重，根據權重值選擇樣例.HUANG S J等人［3］結合支持向量機提出的QUIRE算法也屬于此類，在多個領域具有較好的分類效果，然而存在計算復雜度較高的問題.

使用統計學習的方法選擇未標注樣例得到了深入的研究.MACKAY D、COHN D A等人［4-5］提出使用統計學習的方法來優化目標函數，使用前饋神經網絡等分類器來創建模型.ROY N等人［6］提出直接使用最小化期望風險函數的統計學習方法來選擇未標注樣例，但該方法仍然存在計算信息量較大的問題.WANG Z等人［7］通過極小化經驗風險選擇信息量大及有代表性的未標注樣例.TANG Y P等人［8］引入自步學習選擇易分類的未標注實例，同時選擇符合信息量大等特征，有潛在價值的未標注實例，取得了較好的分類效果.

目前，ZHU X J等人［9-10］提出了使用概率圖模型優化期望風險函數，在優化的同時使用半監督學習來減少標注量，取得了不錯的分類效果.GAD E E等人［11］從標注數據集中引入先驗信息，使用概率圖模型做樣例選擇.這些查詢策略從概率圖模型角度去選擇樣例，為主動學習研究提供了新的視角.

為了解決隨機采樣的性能不穩定問題，以及計算復雜度過高等問題，本文提出使用信息熵作為衡量標準對未標注樣例進行選擇，對選擇的樣例子集合計算平均期望風險，選擇使得平均期望風險最小的樣例進行標注.在真實數據集上進行實驗，實驗結果表明該策略與基準策略相比，時間復雜度較低，有效性較高.

1 基于信息熵的期望誤差減少抽樣估計的主動學習查詢策略

基于信息熵的期望誤差減少抽樣估計的主動學習（Active Learning through sampling estimation of Expected Error Reduction based on Information Entropy，ALEERIE），該主動學習查詢策略的提出是基于看待數據的角度不同，使用期望誤差減小的統計模型選擇查詢樣例偏向于整體數據分布，而信息熵關注的是單獨樣例的信息量.基于信息熵的不確定度采樣策略在選擇特定樣例過程中要有較強的有效性和魯棒性，因此可以結合兩種策略制定混合式的主動學習查詢策略.

基于統計學習的學習策略需要循環遍歷整個未標注數據集，因此存在計算復雜度比較高的問題，具體復雜度是O(N2)，而在基于信息熵的期望誤差減少抽樣估計的主動學習中，使用基于信息熵的抽樣估計以后，復雜度可以降低為O(Q×N).N表示未標注樣例的總數，Q表示使用信息熵進行抽樣估計的數目.

ROY N等人［6］提出使用統計學習中最小化期望風險的辦法來選擇未標注樣例.使用主動學習框架建立的最佳分類器應該是選擇未標注實例以后，人工標注實例并將其加入到訓練數據集，在該訓練數據集訓練模型時能夠減少期望風險，具有最佳的泛化能力.

設訓練樣例x∈D=Rn，實例的標記為y∈Y={y1,y2,…,yk}，對訓練樣例x的條件概率分布為P(y|x)，該分布未知.已標注樣例集合D采用獨立同分布采樣，其聯合概率分布P(x,y)=P(y|x)P(x)，對輸入樣例x，則生成后驗概率(y|x)，因此基于統計學習的期望風險為

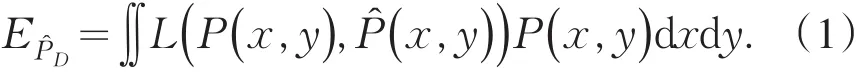
損失函數L用于衡量樣本(x,y)的真實概率分布P(x,y)與后驗概率估計分布(x,y)的差值.本方法采用的損失函數為對數損失函數，

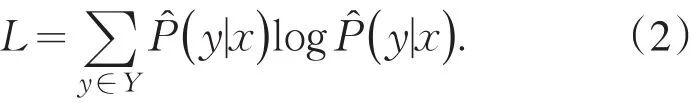
期望風險EP?D優化的目標為選擇最優未標注樣本序列k={x1,x2,x3,…,xk}，其中k表示從未標注樣本中采樣的次數，對于樣本序列k中的每個未標注樣例(x*,y*)，

本策略針對基于未標注樣例池M進行學習，因此學習的范圍確定，對于未標注樣例有確定的估計P(x).定義將未標注樣例(x*,y*)加入已標注樣例集合D產生的新的標注集為D*=D+(x*,y*)，新的標注樣例集D*的分布函數未知，為了能夠有效地計算公式（2），采用已標注樣例集的概率分布來估計當前未標注樣例(x*,y*)，則當前分類器的經驗風險為

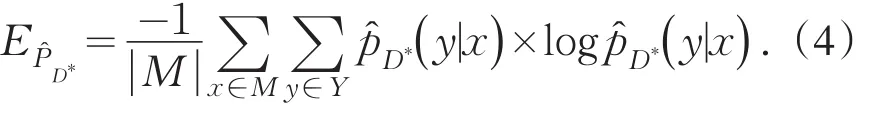
E計算出未標注樣例x*，在y*∈Y情況下期望風險值，y*的真實值是未知的，可以使用已知的概率分布P(x,y)，計算估計概率分布值，將不同的概率分布作為權值，計算最終期望值

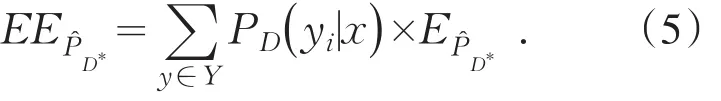
該策略存在計算量過大，復雜度較高等問題.最優未標注樣本序列k的建立過程實際是在對未知分布進行有選擇抽樣過程.簡單的抽樣策略是每次在未標注實例集M循環遍歷每一個樣例，其時間復雜度為O(|M|2).可以選擇隨機采樣，或者預先過濾異常點等方法減少未標注樣例的選擇范圍.

信息熵可以用于衡量未標注樣例的不確定性，作為主動學習的策略具有較強的魯棒性.基于信息熵可以對集合M進行采樣，采樣的過程是計算每個樣例的不確定度，從中選擇不確定度最高的Q個樣例.

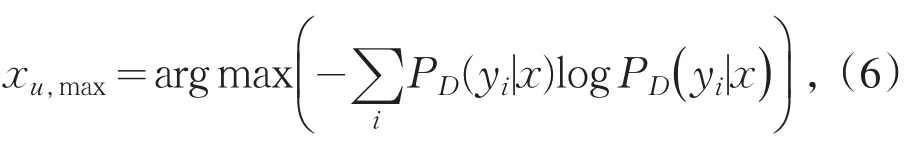
xu,max表示從集合M中選擇的信息熵最高的樣例，以已標注樣例結合D來計算樣例的信息熵值.根據信息熵，選擇不確定度最高的Q個樣例，對Q個樣例計算響應的期望風險，并選擇期望風險值最小的樣例進行手工標注.算法過程如圖1所示.

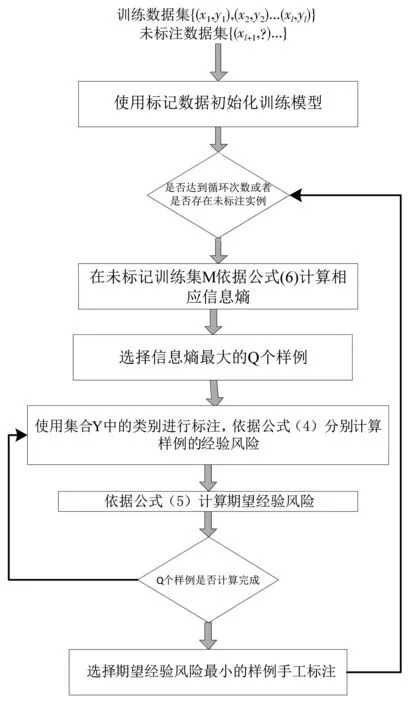
圖1 基于信息熵的期望誤差減少抽樣估計的主動學習查詢策略

算法流程如下：

算法 基于信息熵抽樣估計的統計學習查詢策略.

①Input：初始化標記數據集D={x1，…,xl}，未標記數據集M={xl+1，…,xl+u}，數據標記y1,…,yl，最大循環次數Umax.

⑥在標記數據集上訓練模型.

⑦在未標記訓練集M依據公式（6）計算相應信息熵.

⑧選擇信息熵最大的Q個樣例.

⑨forj=1 toQdo：

⑩對樣例使用集合Y中的類別進行標注，分別加入到訓練集中，重新訓練模型，依據公式（2）計算相應的損失函數.

太和醫院始建于1965年，如今已然成長為四?。ㄊ校┙唤绲鼐C合實力最強的一家三級甲等醫院，醫院服務能力輻射周邊40多個縣市區。

?依據公式（4）計算相應的經驗風險函數.

?根據類別的不同，依據公式（5）計算期望風險函數的期望值.

?選擇使得期望值最小的樣例，進行手工標注.

?end while.

?return 條件概率分布

2 實驗設計

為了驗證基于信息熵抽樣估計的統計主動學習策略的有效性，與隨機采樣過程在多個數據集上進行了對比.隨機采樣過程從未標記實例中隨機選擇若干樣例，選擇使得期望風險最小的樣例進行手工標注.

實驗數據來自于加州大學歐文分校提出的用于機器學習的數據集.選擇其中的tic-tac-toe、transfusion、kr-vs-kp、diagnosis、breast-cancer用于二分類的數據集，該部分數據集經常用于主動學習查詢策略的研究［8］，具體的數據集描述見表1.

表1 實驗中用到的數據集

實驗數據采用分層抽樣對數據集進行劃分，50%用于訓練數據，50%用于測試數據，從訓練數據中取出10%作為初始標注數據集，用于建立模型.實驗隨機重復執行5次，采用交叉驗證，因此數據集產生5×2組數據，取所有數據的平均值為該標注數據點的預測結果.

實驗過程中使用sklearn工具包，分類器選擇隨機森林分類器與logistics回歸分類器，參數使用系統默認參數.分類器的超參數優化對學習策略的影響在后期的工作中會繼續研究.UCI數據集中的類別數據轉換通過sklearn的LabelEncoder類來實現類標的編碼，將屬性轉換為對應的整數值.從未標注實例中選擇子集需要設定超參數Q，超參數Q表示從未標注實例集中抽樣的數目，在本策略中，設定Q為20.

算法的評價指標采用ACCURACY，表示真正例與真負例與所有樣例總和的比值.常見的性能評價指標還有AUC、F1-Measure等，此次實驗選擇的數據集，不存在明顯的類不平衡問題，因此主要在ACCURACY指標上做性能評價.分類結果的混淆矩陣如表2所示［12］.

表2 分類結果混淆矩陣

ACCURACY表示分類模型總體判斷的準確率，是涵蓋了所有分類的總體準確率.

3 結果分析

3.1 標記實例的數量對策略性能的影響

在數據集tic-tac-toe、transfusion、kr-vs-kp、diagnosis、breast-cancer中兩種待比較算法隨著標注樣例的增加性能變化如圖（2）、圖（3）、圖（4）、圖（5）、圖（6）所示.采用隨機森林作為數據集的分類模型，隨后將會考慮其他分類器，以驗證所提的主動學習策略的有效性是否具有一般性.

圖2 數據集tic-tac-toe的ACCURACY性能變化

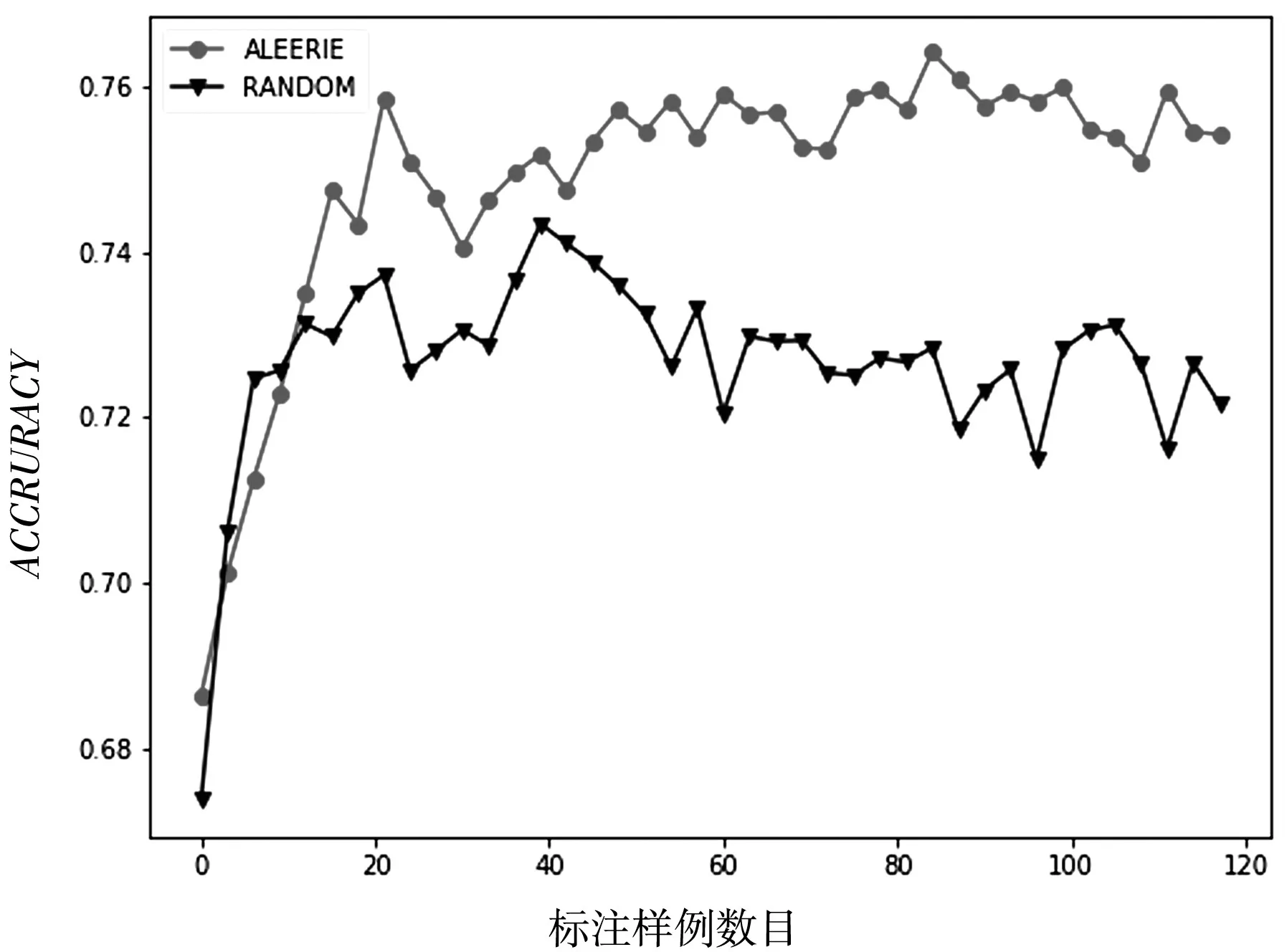
圖3 數據集transfusion的ACCURACY性能變化

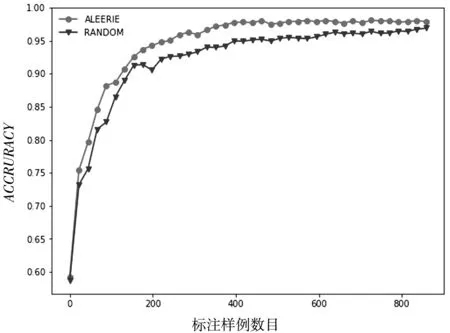
圖4 數據集kr-vs-kp的ACCURACY性能變化

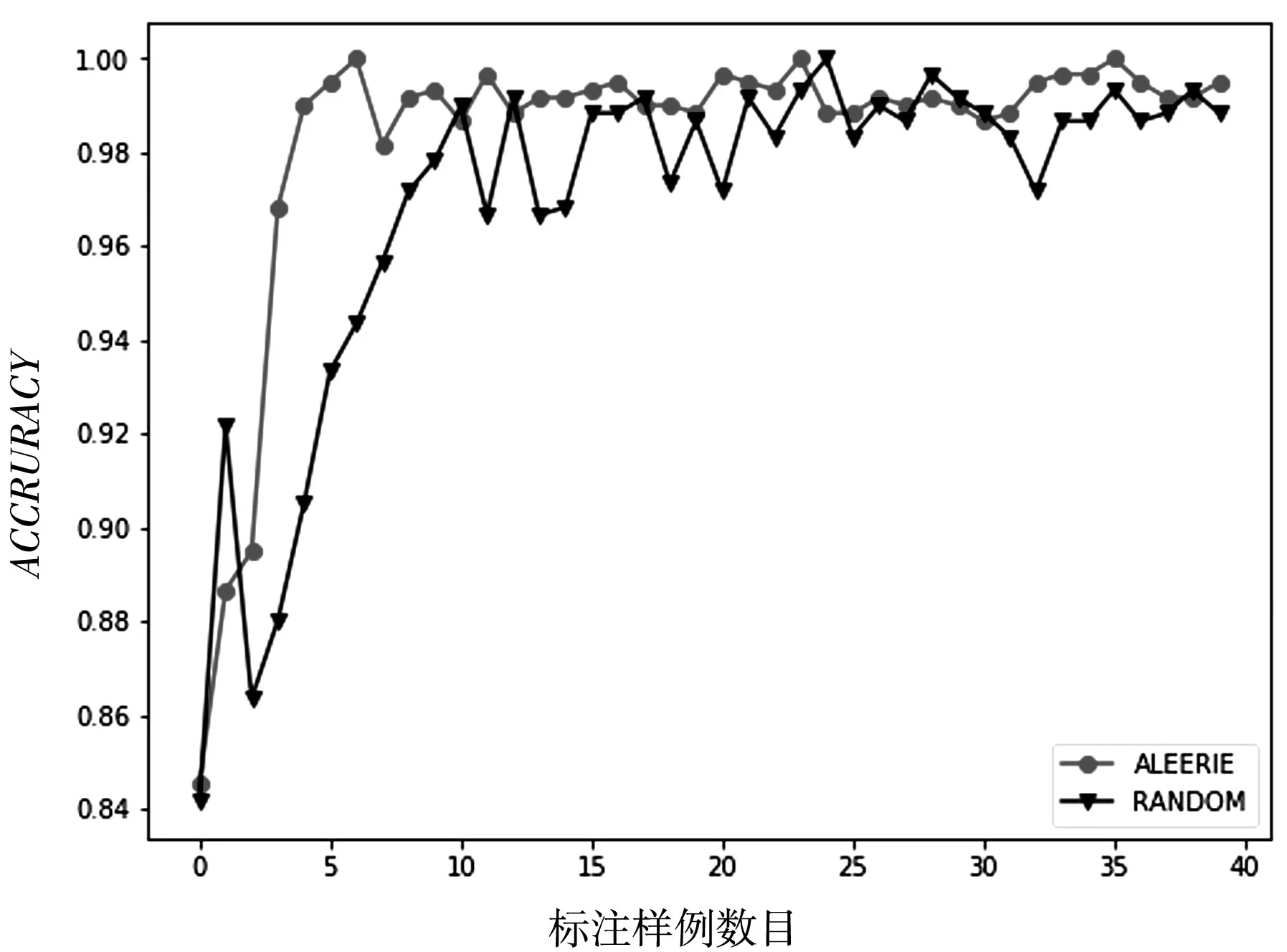
圖5 數據集diagnosis的ACCURACY性能變化

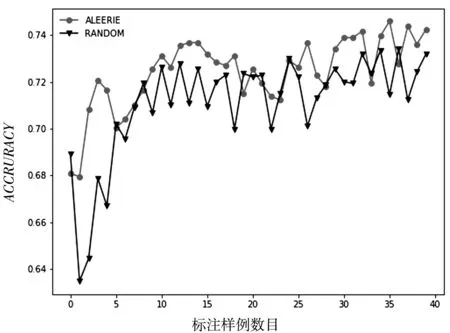
圖6 數據集breast-cancer的ACCURACY性能變化

為了深入研究所提出策略的有效性，在標注數據比例為20%、40%、60%、80%、100%的情況下對兩個算法的結果作win/draw/loss分析.win/draw/loss分析用于描述不同算法對于同一數據集的算法差異.比如標注數據比例為20%時候，在數據集tic-tac-toe上信息熵采樣策略的分類器ACCURACY均值記為Aie，在數據集tictac-toe上隨機采樣策略的分類器ACCURACY均值記為Ar，如果Aie＞Ar，那么win=1，如果Aie=Ar，那么draw=1，如果Aie＜Ar，那么loss=1.表3展示了基于信息熵采樣策略與隨機策略對比的win/draw/loss.

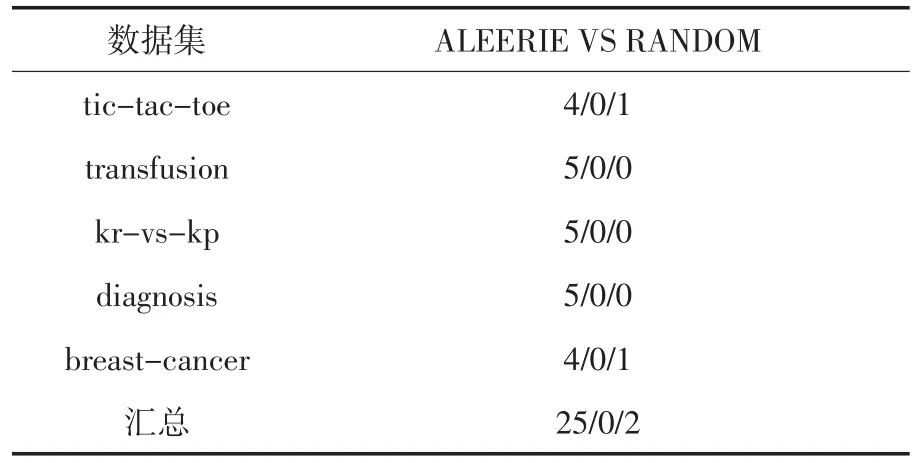
表3 基于信息熵采樣策略與隨機策略的win/draw/loss分析

從以上圖表展示結果可以看出，基于信息熵的抽樣策略比隨機策略在大多數情況下都能達到較好的分類效果，充分說明了基于信息熵策略的有效性.同時也說明了在進行基于統計學習的子抽樣時候，面向個體信息量的選擇優于隨機的選擇.隨著標注樣例數目的增加，主動學習的兩個采樣策略依據不同角度進行抽樣，分類算法的精度都得到了提高，也說明了主動學習方法框架的有效性.但是在數據集diagnosis上也有不同的表現，基于信息熵的策略隨著標注樣例的增加，快速達到較好的分類效果；而隨機采樣策略不但沒有達到較好的分類效果，甚至分類性能出現了較大的波動.這樣說明基于信息熵的策略更加有利于提升模型的分類器精度.從數據集transfusion的性能走勢可以看出，隨著標注樣例的增多，算法性能得到了較快的增長，并且收斂于比較穩定的分類效果，而隨機采樣的策略在達到較好的分類效果以后甚至出現了性能下降的情況.

3.2 基于不同分類器上采樣策略的性能對比

為了充分研究不同采樣策略的性能變化情況，選擇使用其他的分類器對數據集進行建模，通過不同分類器上不同采樣策略的性能對比，為了節省空間，僅僅描述標注數據比例為20%、40%、60%、80%、100%的情況下性能對比情況.表4展示了不同分類器上不同采樣策略的性能對比.

從表4的結果可以看出，不管是采用隨機森林分類器（RF）還是采用邏輯斯蒂回歸分類器（LR），本文提出的基于信息熵的抽樣估計策略大部分情況下都取得了最優的效果，即使在部分情況下沒有達到最優，也并不弱于最優性能很多.由此可以說明，針對不同的分類器或者不同的標注實例比例的情況下，本文提出的基于信息熵的抽樣策略都能有穩定的性能提升.

另外從兩種不同分類器的性能比較情況還可以看出，基于信息熵進行抽樣估計的策略擁有更加穩定的表現，隨著標注樣例的增多，分類性能穩步提升直至收斂到最佳水準.而隨機采樣策略明顯表現出比較強的隨機性與性能的不穩定性.

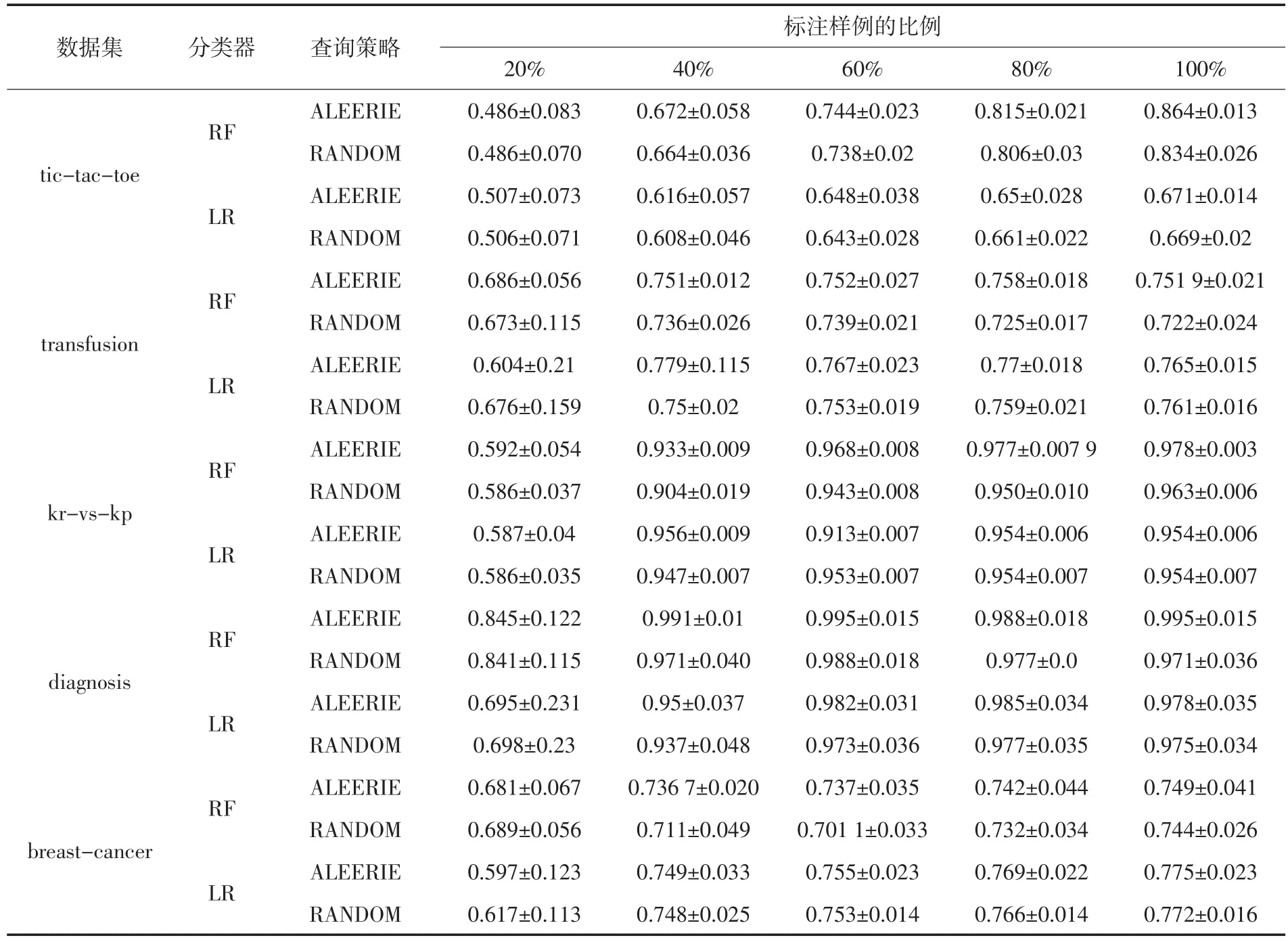
表4 基于配對t檢驗的采樣策略對比試驗

4 結論

本論文提出了在使用基于統計學習的面向期望風險減小的主動學習策略中，通過使用信息熵來進行子抽樣.基于統計學習的選擇策略是從宏觀上選擇期望風險最小的樣例進行標注；而基于信息熵的樣例選擇策略則是從樣例的微觀角度選擇樣例，充分利用樣例本身的信息量，對兩者進行充分的結合有助于選擇既能滿足樣例信息量較高又能滿足期望損失最小的樣例.同時選擇策略有效降低了基于統計學習選擇策略的計算復雜度.在機器學習的常見數據集上的實驗表明，該策略能夠有效地從未標注實例中選擇需要人工標注的實例.后期的研究從其他的子抽樣策略入手，對比研究不同的子抽樣策略對于基于統計學習的主動學習查詢策略的影響.當前研究的數據集采用的都是二分類的數據集，后面可以研究當前策略在多分類數據集上性能的變化情況.除了圖像處理應用領域，未來也可以嘗試將該查詢策略應用于智慧農業等機器學習廣泛應用的領域［13］，從而有效減少數據集的標注成本.