基于排隊模型的大型園區充電站負載能力研究

李西園，封寶華，尚永紅，孫雪吟，解崢，陳時雨

1. 北京衛星環境工程研究所，北京 100094

2. 北京航空航天大學 航空科學與工程學院，北京 100191

電動汽車作為新能源汽車的一種，具有使用過程中污染低、結構簡單、維護方便等優點[1]，目前在北京的純電動汽車數量已經接近20萬輛。相較于傳統燃油汽車的加油站，電動汽車充電站操作簡單、安全性高，但使用時間較長，一般直流充電樁充電時間為1～2 h左右，交流充電樁充電時間可達8 h以上，充電樁的建設是電動汽車中遠途出行的最大制約條件之一[2]。這也導致了電動汽車用戶的充電習慣與燃油車用戶的加油模式存在非常大的區別。大型電動汽車充電站的選址亦與加油站存在區別，一般選擇建設在住宅區停車場、大型商業區、企業園區內部或其他公共設施內部[3]，以降低用戶充電等待的時間成本。

由于充電樁單用戶占用時間長的特點，充電站建設時必須對潛在的用戶數量具有較為精確的估計，充電樁過少可能無法滿足周邊用戶充電需求而導致大量排隊，充電樁過多時則會加劇電網負荷峰谷差，影響電網運行的經濟性和安全可靠性[4]。目前的優化方法包括充電樁軟、硬件改進和通過模型預測充電站的負載量等[5]。其中充電站負載量預測研究主要針對大型公共充電站或出租車充電站[6?7]，通過地區總用戶數量估算充電站單位時間平均用戶數量和平均充電時間。對于用戶的到達間隔一般近似服從負指數分布，對于平均充電時間，選取分布包括負指數分布[8?9]、正態分布等[10?11]，基于排隊模型可求解充電站的平均排隊人數、平均負載率等關鍵指標。對于建立在商業區、工業園區內部的充電站，其平均用戶數量隨時間變化較大，使用平均值進行分析難以反映其最惡劣情況下的排隊狀態。針對企業園區內部的充電樁，為了考慮冬季最惡劣工況，本文選取了2017年12月—2018年2月間某大型工業園區內部的充電樁使用記錄，統計了不同時段用戶數量、平均負載率等參數。基于統計數據建立了不同用戶數量下的排隊模型，通過蒙特卡洛方法對不同用戶數量的工況進行了仿真，對比了不同充電時間分布對排隊關鍵參數的影響，并給出了排隊長度、排隊時間等關鍵指標。最后，本文通過建立的排隊模型對未來更大客流量情況的排隊進行了仿真分析，給出了排隊基本參數。

1 用戶充電習慣統計

本文選取某大型工業園區內部充電站作為研究對象，其主要原因在于：1)該充電站位于某大型工業園區內部，充電用戶較為固定；2)該充電站具有專人管理維護，故障率低；3)該充電站具有完善規章條例，能最大限度降低設備故障、燃油車占位等可能對數據分析產生干擾的因素。充電站共有電動汽車充電樁16個，其中直流充電樁15個，交流充電樁1個。為了減少新用戶注冊對統計數據的影響，僅考慮注冊后充電次數>4的用戶，共計170名用戶。本文統計的2017年12月—2018年2月用戶充電周期的分布圖1所示。

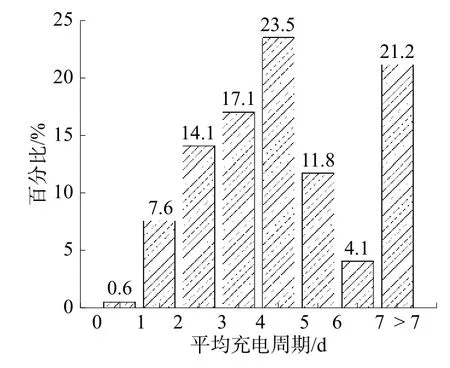
圖1 平均充電周期分布

如圖中所見，在該充電站充電周期2~6 d的用戶占據了70%以上，充電周期7 d以上的用戶亦占據了21.2%左右，可認為這部分用戶亦有在其他充電站或家用充電樁進行充電的習慣。當僅考慮充電間隔1~7 d的用戶時，用戶的平均充電間隔為3.81 d。如圖2為充電樁每次服務充電量分布。

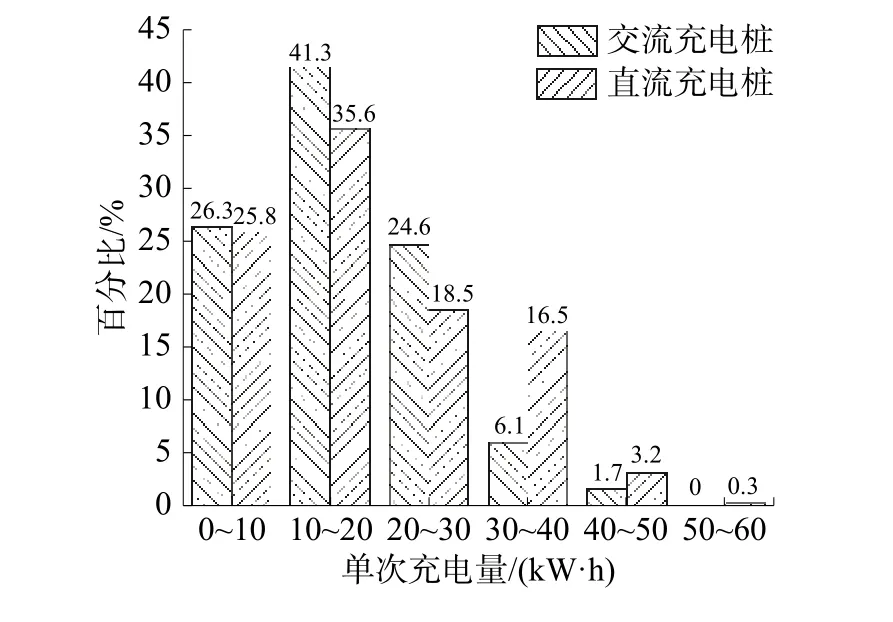
圖2 充電量分布

如圖中所見，選擇每次充電10~20 kW·h的用戶達到了40%以上，而用戶的平均充電量為18.1 kW·h。根據統計數據，目前北京平均通勤單程距離為17.4 km[12]，而一般小型純電動汽車耗電量在 0.15 kW·h·km?1左右[13]，平均充電周期內的電量消耗E可以表示為

式中：s為用戶日平均單程通勤距離，km/次；t為平均充電周期，d；w為小型純電動汽車單位里程耗電量，kW·h·km?1；n 為用戶單日通行次數，次/d，考慮用戶主要為上下班通勤用途，n取2 次/d。由此可得平均充電周期內的電量消耗約為19.9 kW·h，與該充電站的統計數據偏差約為10%左右。考慮到大型園區在地理分布上的差異性和離散性，這個偏差是可以接受的。

對于用戶在充電時間上的選擇，充電樁在一天內的平均占用率變化曲線如圖3所示，其中1號為交流充電樁，2~16號為直流充電樁。

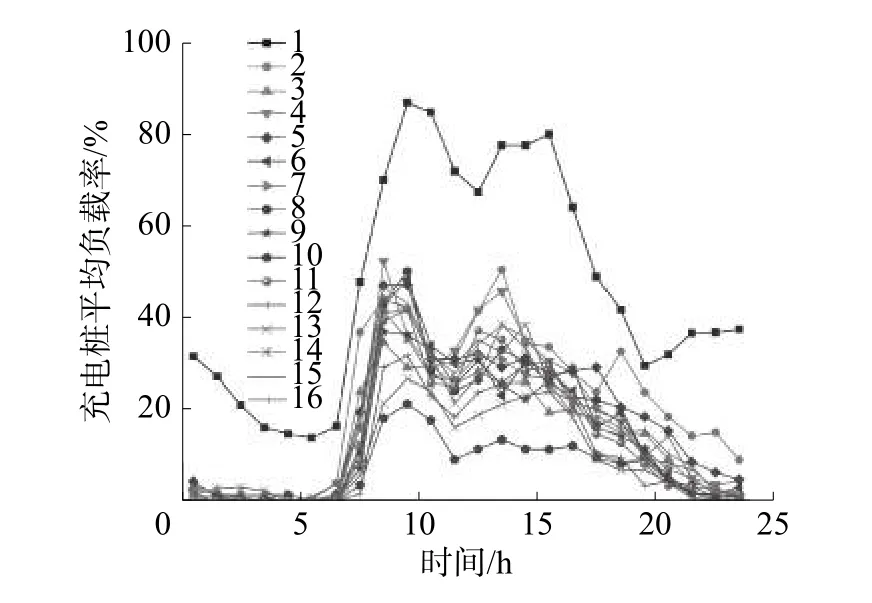
圖3 充電樁平均占用率

如圖3所示，在工業園區內部的充電站負載率呈現了非常強的時間相關性，即在晝間負載率較高，夜間負載率較低。本文對67 d內充電站在工作日晝間、工作日夜間、非工作日晝間、非工作日夜間的抵達人數進行了統計，發現在工作日晝間 (7:00—19:00)，平均抵達人數約為 3.99 人/h，占據一周內總抵達人數的80.0%。同時，如圖中所見，目前直流充電樁在高峰時間占用率僅為20%~50%，用戶到達充電站后往往可以立即開始充電而不需要進行排隊，即系統記錄的開始充電時間可以代表用戶的到達時間。但對于用率較高的交流充電樁，后臺往往存在多位用戶對其狀態進行監視，并準備前往充電。無法獲得后臺排隊的用戶數量將大大降低模型的精確度，故本文對排隊模型的仿真主要針對直流充電樁進行。

2 充電樁排隊模型

2.1 排隊模型建立

用戶在充電站排隊充電的事件可以使用排隊模型進行仿真，一般而言，用戶到達充電站的時間間隔服從負指數分布，其概率密度為

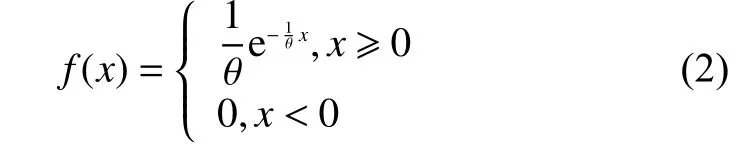
式中θ為負指數分布的尺度參數，min，即排隊模型中用戶到達的平均間隔。圖4為工作日晝間的用戶到達直流充電樁的間隔分布與負指數分布對比。

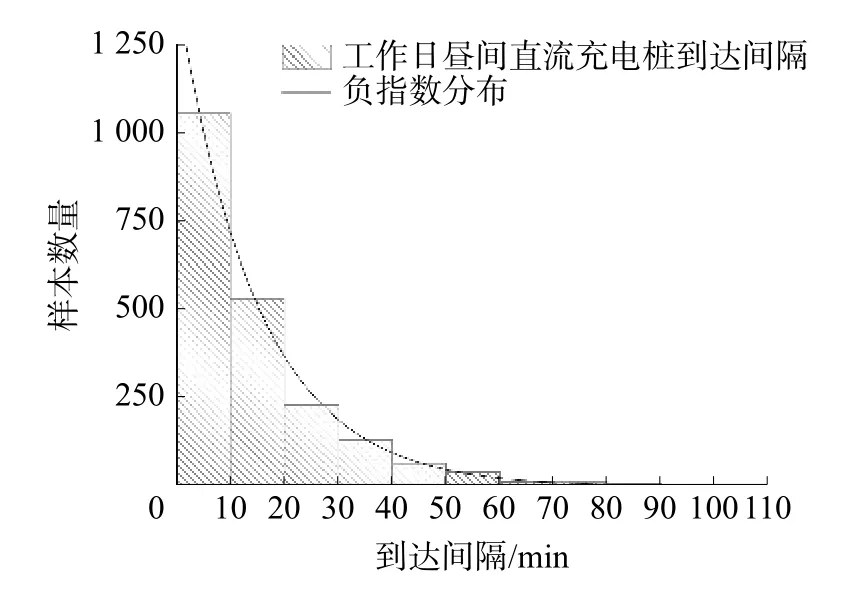
圖4 用戶到達間隔分布

如表1所示為對工作日晝間(7:00—19:00)、工作日夜間(19:00—0:00)、非工作日晝間、非工作日夜間用戶到達時間負指數分布擬合參數和K?S檢驗結果，其中N為樣本量，E、SE分別為負指數分布尺度參數θ的估計值和估計值標準誤差，p為顯著性水平，h為檢驗結果。

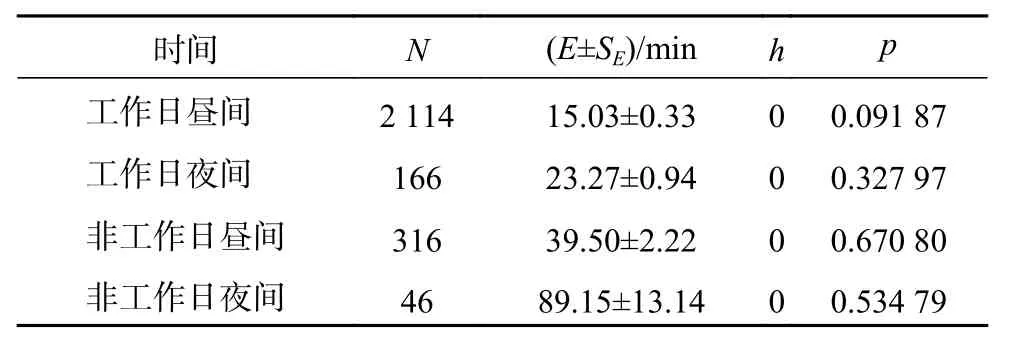
表1 用戶到達間隔時間負指數分布擬合與 K?S 檢驗結果

如表中所見，在顯著性水平0.05的情況下，不能拒絕數據服從負指數分布的假設。

針對充電樁的平均服務時間，目前研究選擇的分布包括負指數分布、正態分布等。本文對交流充電樁、直流充電樁平均服務時間進行了統計，圖5、6為該充電站交流、直流充電樁的使用時間分布與幾種典型分布的對比。

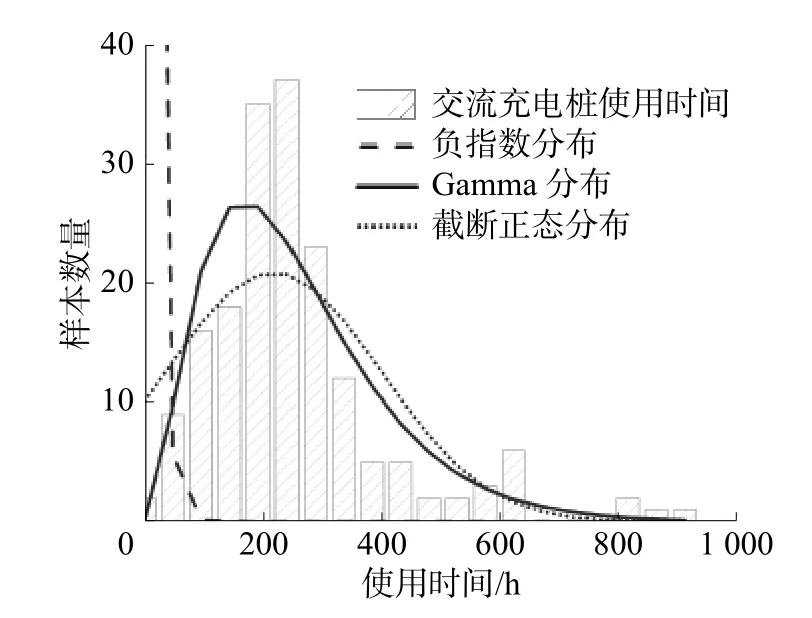
圖5 交流充電樁服務時間分布

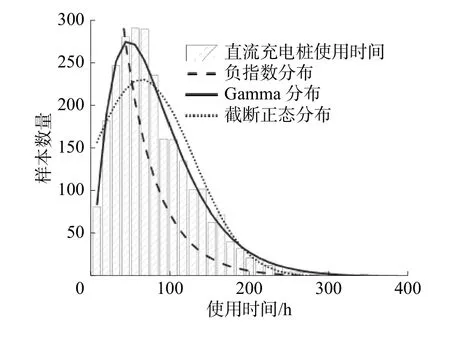
圖6 直流充電樁服務時間分布

表2、3為交流、直流充電樁使用時間分布擬合參數和K?S檢驗結果，其中Exp、Norm、Gamma分別為負指數分布、截斷正態分布和Gamma分布，E、SE、M分別為分布參數的估計值、估計值標準誤差和分布均值，θ為負指數分布的尺度參數，μ、σ為截斷正態分布的位置參數和尺度參數，α、β為Gamma分布的形狀參數和尺度參數，p為顯著性水平，h為檢驗結果。

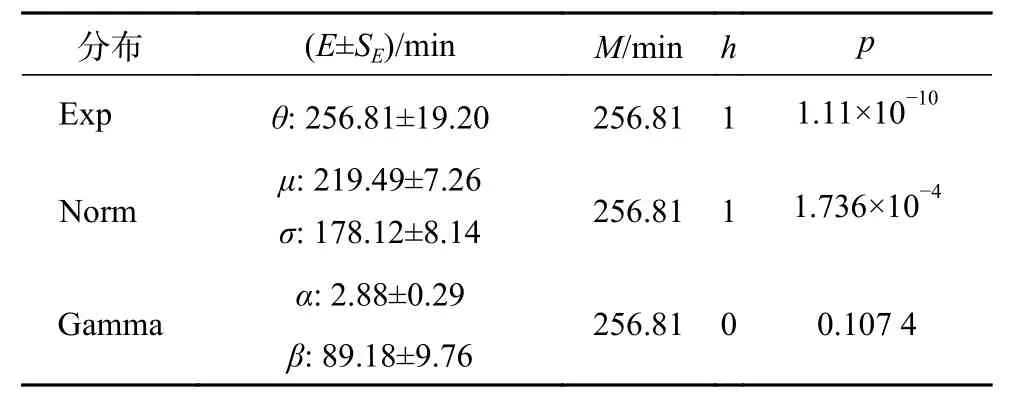
表2 交流充電樁充電時間分布的 K?S 檢驗結果

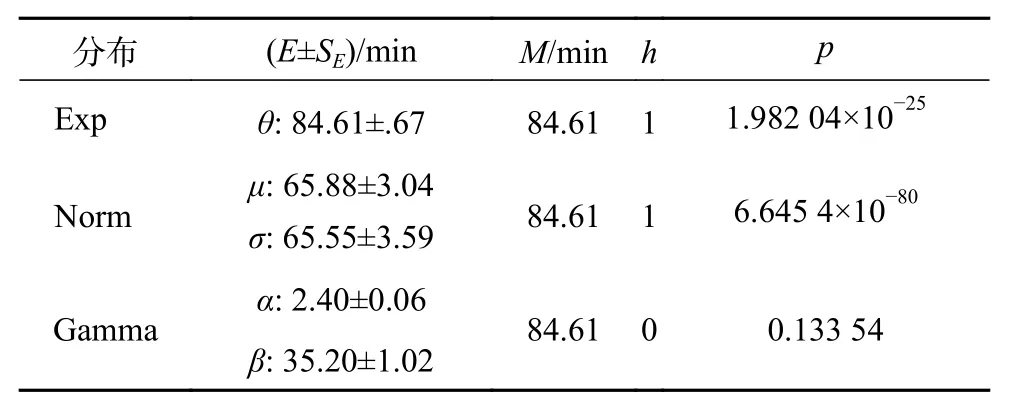
表3 直流充電樁充電時間分布的 K?S 檢驗結果

如表2、3所見，在顯著性水平0.05的條件下，該充電站內充電樁的服務時間長度近似服從Gamma分布，其概率密度函數為

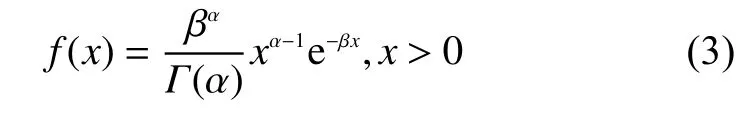
式中：α為Gamma分布的形狀參數；β為Gamma分布的尺度參數。本文基于分布擬合數據建立了M/G/k排隊模型，即到達時間間隔服從負指數分布，平均服務時間為一般分布的多服務臺模型，如圖7所示。用戶通過客戶端APP程序查看充電站是否有空閑充電樁(單隊列)，并抵達充電站尋找空閑充電樁進行充電(多服務臺)。

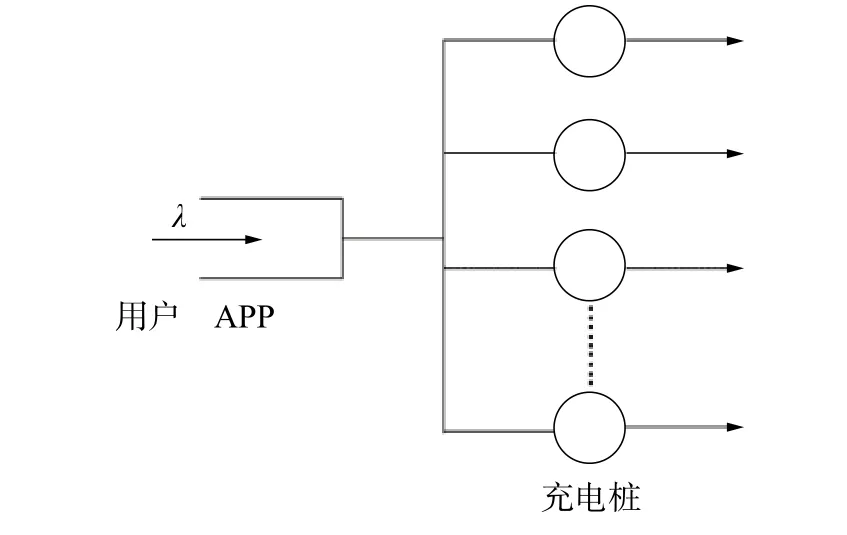
圖7 充電站排隊模型

目前對于M/G/k排隊模型尚沒有公式化的推導過程，平均等待時間和平均排隊長度等指標沒有明確的數學表達式，可采用近似公式給出[14]。但對于不同隊長的概率，則較難通過經驗公式求解。本文基于MATLAB對M/G/k排隊過程進行了蒙特卡洛仿真。為了對不同服務時間分布對排隊模型的影響進行分析，除對現有4個時段的工況進行仿真外，本文還對用戶持續增長后工作日晝間、工作日夜間和非工作日晝間的工況進行了仿真，仿真工況如表4所示。

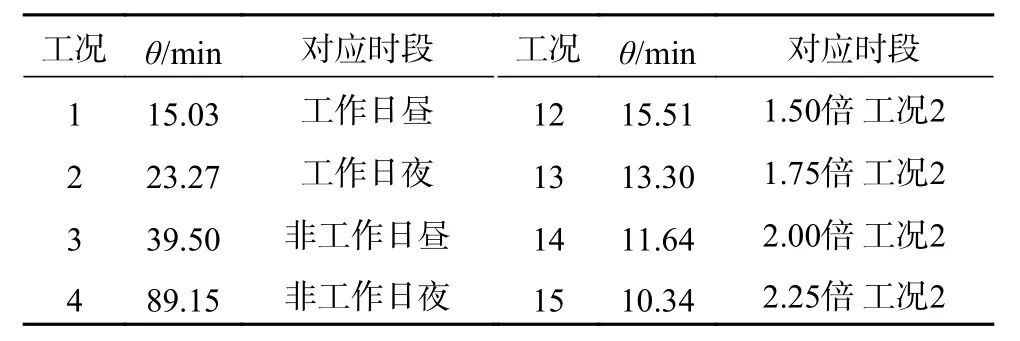
表4 仿真工況

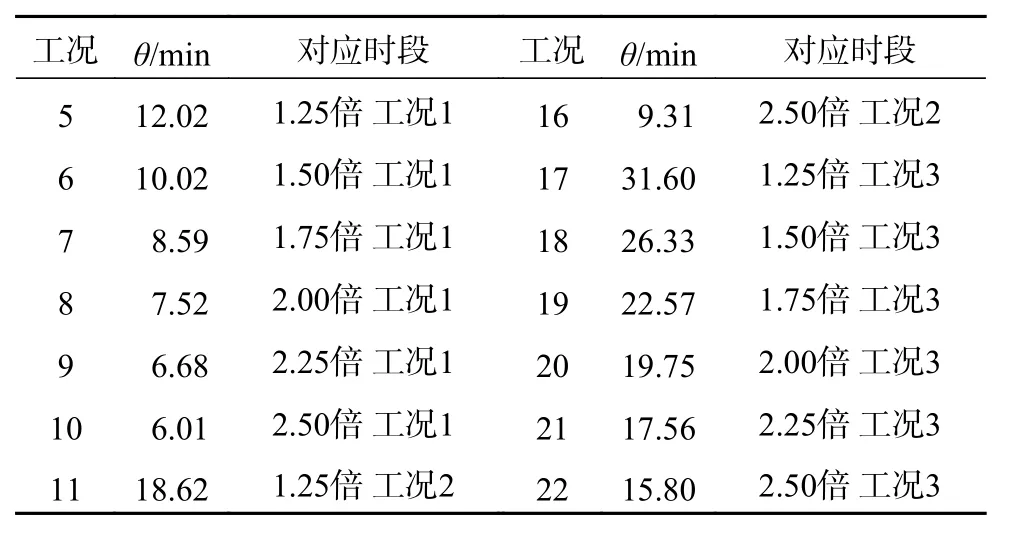
續表

其中仿真工況1~4基于現有統計數據，對不同時段的排隊狀態進行模擬，仿真工況5~10為用戶增長后的工作日晝間工況，仿真工況11~16為用戶增長后的工作日夜間工況，仿真工況17~22為用戶增長后的非工作日晝間工況。假設用戶的充電習慣不隨用戶數量增長發生改變，客流量隨用戶數量線性增長，則可建立5~22工況用戶到達時間間隔分布的尺度參數θ與對應工況當前參數間的聯系：

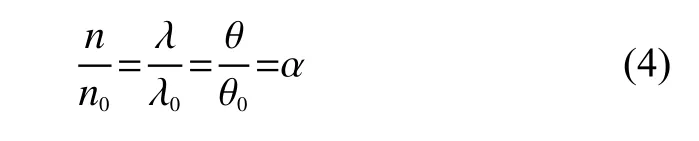
2.2 數據分析

本文分別對服務時間服從負指數分布、截斷正態分布、Gamma分布的條件進行了40次仿真，為了對蒙特卡洛模型的收斂性進行評估，應對多次仿真結果的關鍵參數離散度進行分析。由于各參數量綱、均值不同，選用離散系數Cν作為收斂判據，其可以對量綱、均數不同的多個數據集的離散程度進行比較[15]，表達式為

式中：σ為樣本的標準差；μ為樣本的平均值。

當客流量較低時，排隊時間、排隊人數、無空閑充電樁概率接均接近于0，無法對收斂程度進行反映，選取其中數值大于10?4的參數進行統計。表5為1~4工況排隊關鍵參數的離散系數，其中W為用戶在充電站平均停留時間，Wq為用戶在充電站的平均排隊時間，Ws為用戶在充電站的平均服務時間，L為系統中平均人數，Lq為平均排隊人數，P為無空閑充電樁的概率。

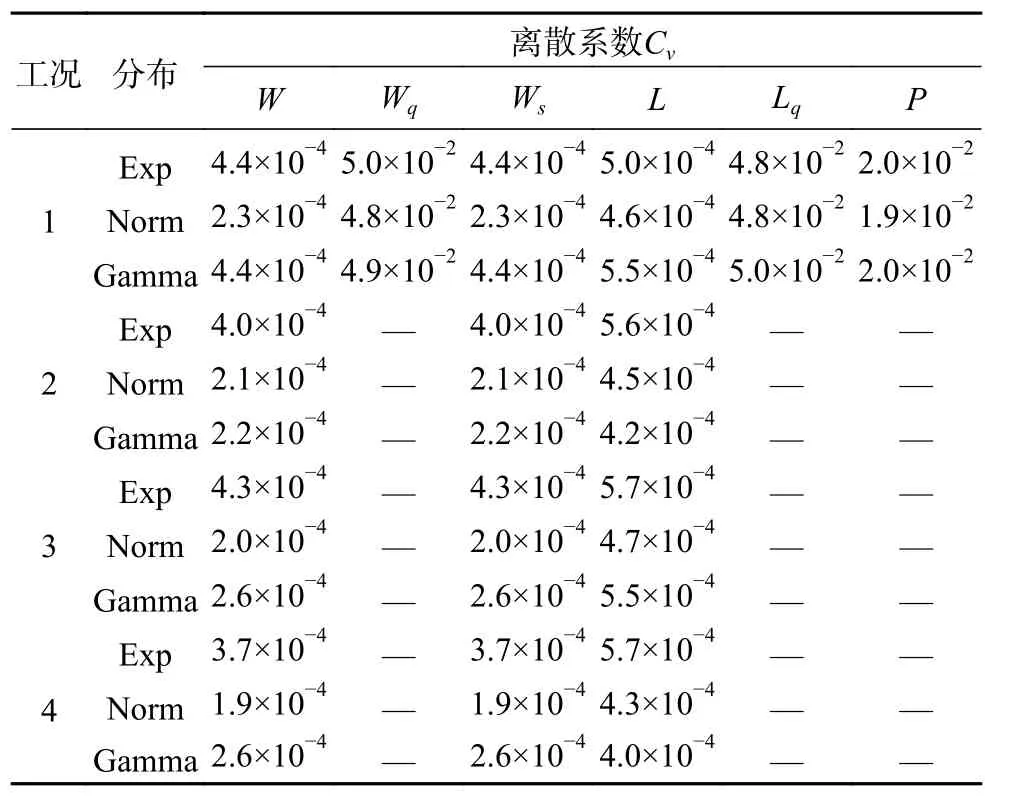
表5 關鍵參數的離散系數 Cν

如表中所見，統計參數的離散系數均在0.05以下，即多次蒙特卡洛仿真獲得的結果非常接近，可以代表該排隊模型的關鍵參數。圖8為通過蒙特卡洛仿真方法模擬的排隊過程中，不同工況條件下穩態時系統內用戶數量的概率分布；圖9為客流量繼續增加時系統內用戶數量概率分布。

圖8 不同時段系統內用戶數量分布

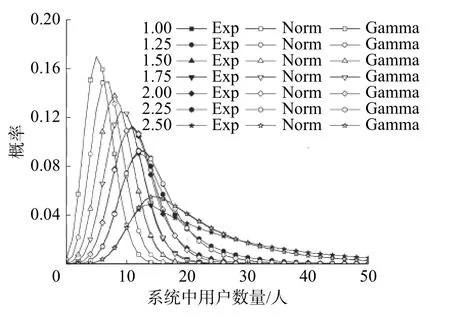
圖9 不同客流量下系統內用戶數量分布

如圖中所見，對于系統負載率較低的工況，即平均排隊長度較小時，由于用戶發現空閑充電樁的幾率較高，充電服務時間的分布形式對系統中用戶數量影響很小。隨著充電人數的增加，服務時間服從截斷正態分布與Gamma分布計算結果較為接近，負指數分布則產生了較大差異。表6為工作日晝間用戶數量繼續增長時的排隊關鍵參數列表。

表6 不同用戶數量時排隊模型的關鍵參數

如表中所見，在充電樁客流量較低時，由于不同服務時間分布的數學期望一致，排隊時間等關鍵指標差異不大。隨著客流量增大，服務時間的分布對平均排隊長度、平均排隊時間均會產生影響，其中截斷正態分布與Gamma分布的計算結果較為接近，負指數分布的計算結果則偏差較大，這與文獻[10]的結論是相似的。即針對電動汽車充電樁排隊優化的問題中的服務時間分布，應選取與實際情況最為接近的Gamma分布或截斷正態分布。如圖10、11為用戶數量增長時，工作日晝間、工作日夜間、非工作日晝間的排隊平均等待時間和平均排隊長度變化趨勢。

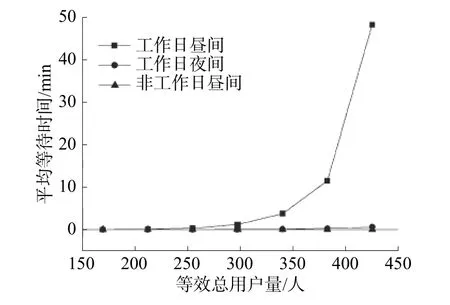
圖10 平均等待時間

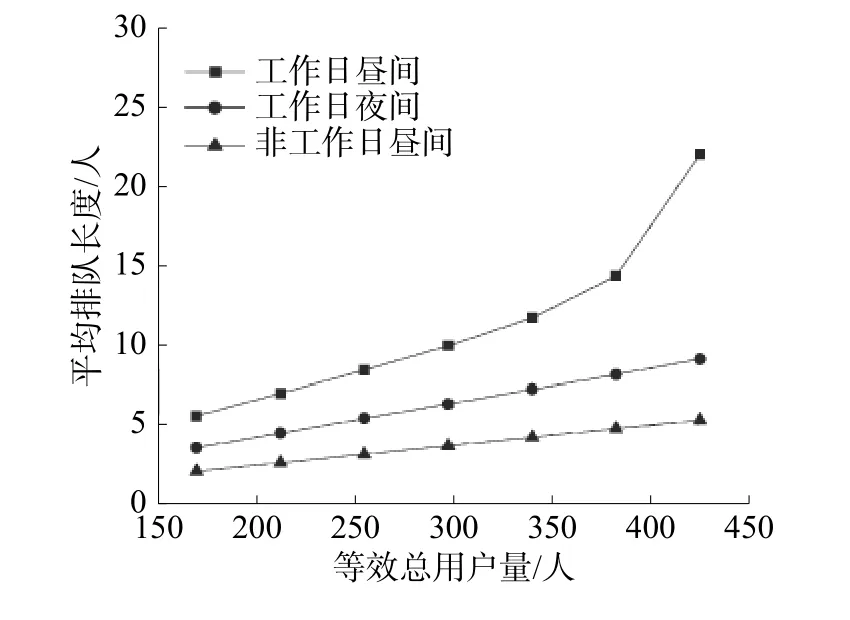
圖11 平均排隊長度

如圖中所見，對于工作日夜間、非工作日晝間的關鍵參數隨總戶數量的增加而平穩增長；對于工作日晝間工況，當總用戶達到383人以上時，平均等待時間和平均排隊長度迅速增加，可能達到40 min以上。即針對大型園區內部充電樁建設數量問題，當用戶充電習慣和現有情況一致時，充電樁數量不應低于0.04樁/人，否則可能導致高峰時段充電等待時間過長。

3 結論

本文針對大型園區內部電動汽車充電站的規劃、建設問題，整理了3個月間某大型工業園區內部充電站的使用信息，統計了用戶在充電周期、充電量、服務時間上的習慣；在現有用戶負荷的基礎上，基于M/G/k排隊模型，建立了大型園區內部直流充電樁的排隊仿真模型；通過蒙特卡洛方法給出了不同時段充電站的平均人數、排隊長度等參數；分析了不同服務時間分布所帶來的影響，并對未來客流量進一步增加時的關鍵參數進行了仿真，得出如下的結論：

1）大型園區內部充電樁使用率隨時間變化存在較大波動，平均充電人數可相差10倍以上，當計算充電站對于區域電網負載影響時，應當考慮其工作日晝間的工況。

2）充電樁服務時間近似服從Gamma分布，充電樁負載較低(排隊時間Wq≈0)時，排隊模型的關鍵參數僅和分布的數學期望有關，此時各種分布計算結果很接近。隨著客流量增大，模型間差異逐漸增大，選取與實際情況最接近的Gamma分布或截斷正態分布計算結果較為接近，均可用于對充電站的排隊估算。

3）針對大型工業園區內部的充電樁規劃、建設問題，當僅考慮直流充電樁時，若用戶充電習慣不發生明顯變化時，充電樁的建設數量不應低于0.04樁/人，否則可能導致高峰時段排隊時間長于30 min以上。對于其他情況下的充電樁占用率估算，可使用本文建立排隊模型進行計算。