最小二乘法分析工作臺平面度誤差

王文超

摘? 要：文章根據中國技能大賽——第八屆全國數控技能大賽，數控機床裝調維修工賽項中關于數控機床幾何精度中關于工作臺的平面度的檢測要求，利用最小二乘法對工作臺的平面度進行分析，文章將系統介紹利用最小二乘法對工作臺的平面度誤差進行分析。

關鍵詞：最小二乘法;平面度誤差;工作臺

中圖分類號：TG83 文獻標志碼：A 文章編號：2095-2945（2019）34-0132-03

Abstract： According to the requirements of the flatness of the worktable in the geometric accuracy of CNC machine tools in the Eighth National CNC Skills Competition， this paper presents the testing requirements of the flatness of the worktable in the geometric accuracy of CNC machine tools in the Eighth National CNC Skills Competition. The least square method is used to analyze the flatness of the worktable. In this paper， the least square method is used to analyze the flatness error of the worktable.

Keywords： least square method; flatness error; worktable

引言

在GB/T17421.1-1998《機床檢驗通則第1部分：在無負載精加工條件下機床的幾何精度》標準中，對平面度的定義及檢測工具提出原則要求。本文依據標準要求，結合機床行業實際情況，對工作臺平面度檢測方法及數據處理做詳細介紹。

平面度誤差是指被測實際表面對其理想平面的變動量。理想平面是評定平面誤差的評定標準，當理想平面不同時，求得的平面度誤差值也就不同。確定理想平面的方法可用簡便法、最小包容區域法及最小二乘法。本文將運用最小二乘法來確定理想平面，并求得機床工作臺平面度的誤差。與其他方法相比，最小二乘法能準確而充分地利用全部原始觀測數據所提供的信息，較客觀地評價機床工作臺的平面度誤差，而且可直接運用于電子計算機運算，使平面度誤差的計算達到迅速準確、可靠的結果。

1 測量方法

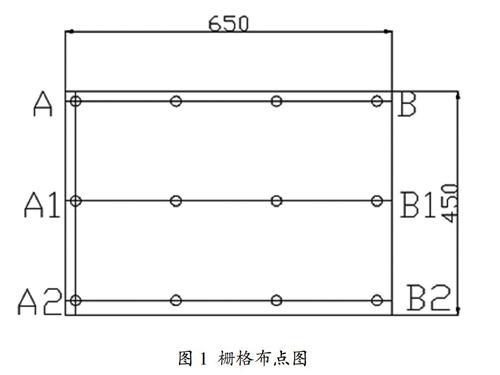
采用最小二乘法評定數控機床工作臺平面度誤差，對于工作臺面的平面度原始觀測數據的獲得，可用柵格式布置被測實際表面上的測量截面和測點，選擇測量截面的方向與被測實際表面縱、橫向平行。比賽設備為紐威機床，工作臺尺寸為650mm×450mm，所用測量儀器為長度200mm測量精度0.02/1000mm的水平儀。根據被測量平面的形狀和尺寸，選擇合適的布點形式，布點形式如圖1所示。按照布線方式依次測量，逐線首尾銜接地進行測量，并同時記錄各點示值。在本數控加工中心工作臺上從A點開始檢測，檢測順序首先檢測橫向，測量順序為A→B、A1→B1、A2→B2。縱向測量為起點為A點，測量方向為A→A2。

下面將以A→B測量方向為例說明測量方法：首先將水平儀縱向放置在工作臺面上，左端距離工作臺左端面20mm左右，待水平儀穩定后，讀取水泡相對選定基準線移動距離，以水平儀上水泡兩端先選中的任意一條為基準線，一般選大線為基準線。水泡在基準的左側為正，右側為負，讀出第一段的測量數據，并記錄。首尾相接將水平儀移動到第二段測量臺面上，根據水泡在基準線的位置讀出正負及數據并記錄，以此類推。在測量過程中應注意，橫向三條線及縱向一條線的讀數基準均為A→B線的讀數基準;每條線測量完畢后都應返回原點，已驗證水平儀是否是回零，如不回零，需重新檢驗。根據以上方法測量，所得的水平儀讀數見表1。

2 數據處理

水平儀的讀數為水平儀首尾兩端相對水平面的高度差，以過起點A的水平面為基準轉換平面，按照hmn=gil+il公式轉換基面的高度值zij見表2。

表2中的數據是水平儀中的格數值，現在我們將格數值轉換為線值（mm）。已知水平儀的長度為200mm測量精度為0.02/1000mm。轉換式如下：

0.02mm/1000mm×200mm=0.004mm=4μm

將表2中，水平儀測量的數據（格）轉換成線性值的數據，每個數據直接乘以4μm，轉換后的數值見表3。

3 平面度誤差最小二乘法的評定

最小二乘法評定平面度誤差就是以最小二乘中心平面為理想平面進行平面度評定的方法，所謂最小二乘理想平面就是指空間點距其距離最小的平面。一般平面方程的表達式為：

對于通過試驗給定的數據（xi，yi，zij），S是a1，a2，a3的非負二次式，所以最小值一定存在，根據極限定理，a1，a2，a3應是下列方程的解：

將該正規方程進一步簡化為：

根據方程組（2）可求解出a1，a2，a3，即可得空間中mn個點（xi，yi，ij），平面度誤差可由下式求得：

4 應用最小二乘法對工作臺進行誤差評定

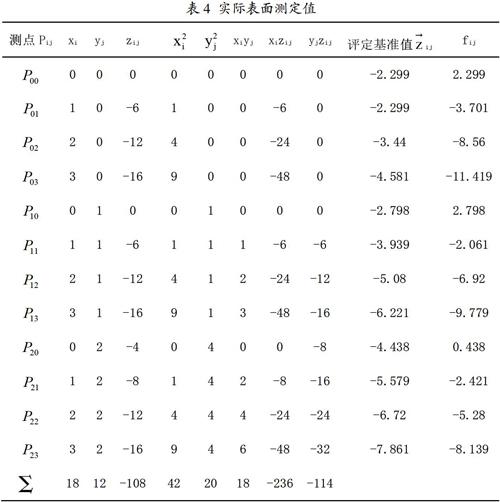
根據最小二乘法對平面度誤差的評定方法，下面對最小二乘法的數據進行處理。將水平儀測定的數據，根據圖2轉換成各點數據。建立實際表面各測點在直角坐標系中的坐標值（xi，yi，zij）列于表4中。則可按式（2）可以求得：a1=-1.141，a2=-1.64，a3=-1.158，則被測實際表面的評定基準方程為：ij=-1.141xi-1.64yj-1.158，因此可以用式（3）算出被測實際表面上各測點相對于此評定基準值得誤差見下式：

取表4中被測實際表面上各測點相對于評定基準值得最大正、負誤差的絕對值之和作為工作臺面整體的平面誤差，即f=fmax-fmin=14.217？滋m。

5 結論

最小二乘法評定平面度誤差，能夠準確地和充分地處理原始測量數據，比較客觀地評定平面度誤差。尤其是在評定尺寸較大的平面時，最小二乘法的優勢更能體現出來，采用最小二乘法進行簡單的運算，不僅容易理解和掌握，而且可以較方便的求得平面度誤差。采用其他方法時，計算繁瑣不易實現編程自動運算。采用最小二乘法可以較方便的采用辦公軟件就可實現自動運算，大大降低了平面度誤差的求解難度。

參考文獻：

[1]張昉.平面度誤差的最小二乘法分析[J].機械制造與自動化，2002（03）：17-19.

[2]李瑞敏.平面度的水平儀檢測及其數據的MATLAB處理[J].組合機床與自動化工技術，2013（3）：39-41.

[3]GB/T17421.1-1998.平面度誤差檢測[S].北京：中國標準出版社，1998.

[4]周景亮.大型平面平面度誤差的可視化數據處理[J].機床與液壓，2009，37（10）：130-132+136.