雙側雙級雙圓弧螺旋錐齒輪章動減速器動力學分析

吳亞強，姚立綱，張 俊，蔡永武，謝志宇

(福州大學機械工程及自動化學院,福建 福州 350108)

0 引言

章動減速器是基于天體行星運動原理而提出的一種新型傳動形式，具有結構緊湊、傳動比大、傳動效率高等特點，可望廣泛應用于機床、儀表、石化、航空等各類傳動裝置中.章動減速器的研究日益引起國內外學者的重視.Fanghella[1-2]通過建立章動錐齒輪行星齒輪系的動力學模型，得到了消除內部慣性力的平衡條件，并通過仿真試驗進行驗證.Saribay[3]分析了錐齒輪章動傳動系統齒面受載性能和傳動性能.姚立綱[4]提出將雙圓弧齒形作為章動傳動螺旋錐齒輪的基本齒形，建立了雙圓弧螺旋錐齒輪齒面數學模型，完成了雙圓弧螺旋錐齒輪章動傳動三維虛擬樣機的運動學、動力學實時仿真.王廣欣[5]采用ADAMS對章動面齒輪傳動模型進行動態嚙合力仿真，分析章動面齒輪副動態嚙合力的變化規律.李璐瑤[6]研究了章動傳動冠狀齒輪的齒形嚙合原理,完成了減速器的運動仿真和動力學仿真.謝志宇[7]借助ADAMS建立雙側雙級雙圓弧螺旋錐齒輪傳動章動減速器的多體動力學模型，并對章動減速器進行了動力學特性仿真.

以上文獻取得了許多有價值的研究成果，但研究對象多為借助軟件對章動齒輪進行動力學仿真.由于雙圓弧螺旋錐齒輪結構的復雜性，通過建立雙圓弧螺旋錐齒輪章動傳動系統非線性微分方程求解其振動響應的研究相對較少.通過對雙圓弧螺旋錐齒輪章動減速器的動力學分析，可對章動傳動系統動態特性、振動穩定性進行預估、分析，具有現實指導意義.有鑒于此，本研究以雙側雙級雙圓弧螺旋錐齒輪章動減速器為例，在計入時變嚙合剛度、嚙合阻尼、齒側間隙、傳遞誤差等因素的情況下，建立章動傳動系統彎-扭耦合非線性動力學模型，采用Runge-Kutta法進行數值計算，并研究了激勵頻率和支承剛度對其動態特性的影響，為后續章動減速器結構改進、動態優化設計提供參考依據.

1 動力學建模

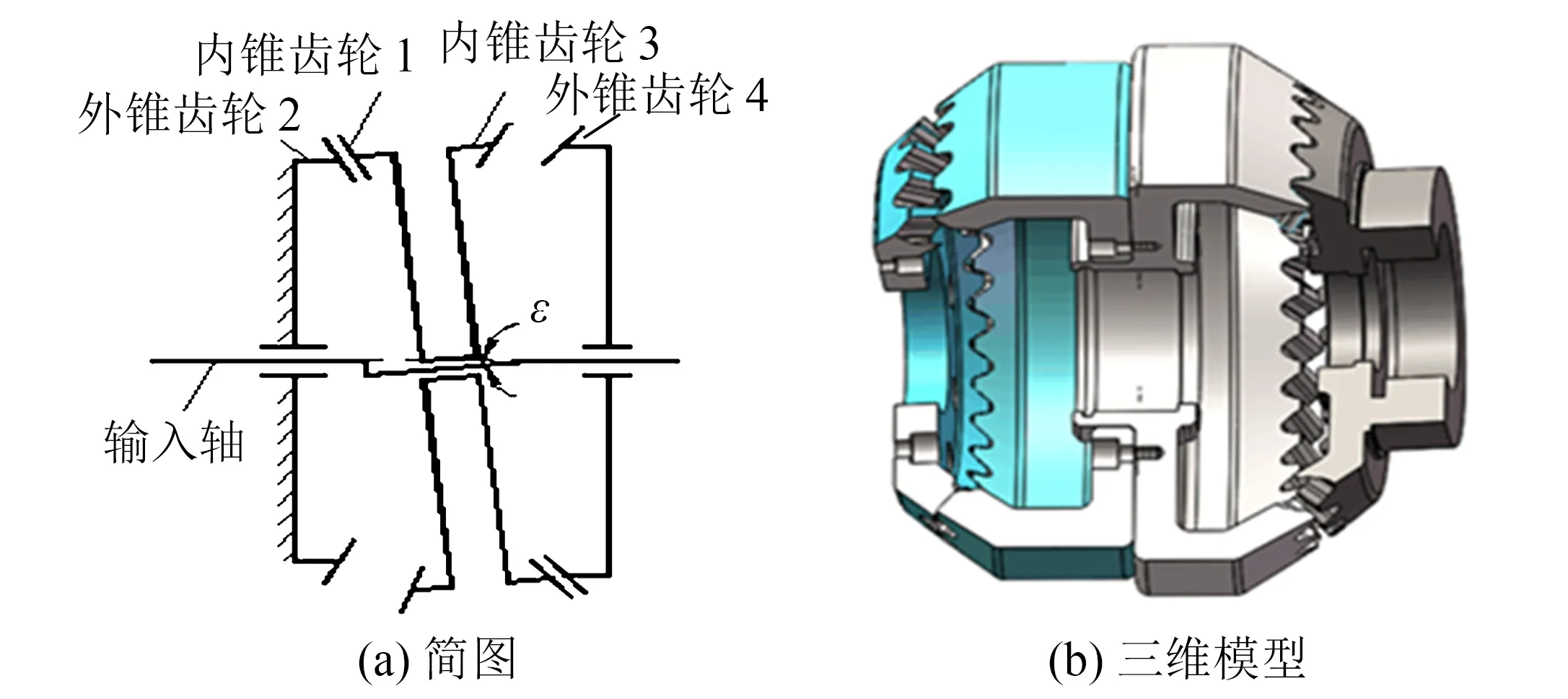
圖1 雙側雙級章動減速器機構簡圖傳動系統Fig.1 Schematic diagram of two-stage bilateral meshing nutation drive

雙側雙級章動減速器機構簡圖如圖1所示，三維模型如圖2所示.兩級齒輪副在徑向方向上為“一上一下”式嚙合，即第1級齒輪副(內錐齒輪1和外錐齒輪2)在一側嚙合，第2級齒輪副(內錐齒輪3和外錐齒輪4)在相反的另一側嚙合.內錐齒輪1、3固連在一起，做章動運動，稱為章動齒輪.外錐齒輪2與機架固連，輸入軸的水平軸線與章動齒輪所在傾斜軸線的夾角為章動角ε.齒輪副主要參數如表1所示.

表1 雙側雙級章動減速器齒輪參數Tab.1 Gear parameters of two-stage bilateral meshing nutation drive

1.1 彎-扭耦合模型

為方便雙側雙級章動減速器傳動系統動力學建模，不失一般性，作如下假設：1)不考慮齒輪嚙合時的齒面摩擦；2)系統阻尼視為一般粘性阻尼；3)由于內錐齒輪1和內錐齒輪3固連在一起，視其為一體，即內錐齒輪1和內錐齒輪3具有相同的自由度，兩齒輪的振動位移相同，兩齒輪之間不產生相對扭轉.基于上述假設，將各齒輪視為集中質量和集中慣量，輸入軸視為剛體，軸承的彈性支承通過彈簧和阻尼器來模擬.采用集中參數法建立章動減速器傳動系統的彎-扭耦合分析模型，如圖2所示.

在圖2中，內錐齒輪1和內錐齒輪3的端面重合且錐點重合于一點O,以此點為原點建立兩個坐標系：空間嚙合坐標系O-xyz和隨章動齒輪轉動的動坐標系O-x0y0z0，其中：y軸與y0軸重合，z軸與z0軸的夾角為章動角ε;T2和T4分別為輸入力矩和負載力矩;xi、yi、zi(i=13,2,4)分別為各齒輪在x、y、z方向的平移振動位移，θi(i=13,2,4)為各齒輪的扭轉位移；kpq、cpq(p=13,2,4;q=x,y,z)分別為各齒輪在3個坐標方向受到的支承剛度和支承阻尼；km j、cm j、en j(t)(j=1,2)為各齒輪副的時變嚙合剛度、嚙合阻尼、法向靜態傳遞誤差；fm j(j=1,2)為由齒側間隙構成的非線性力-位移函數.

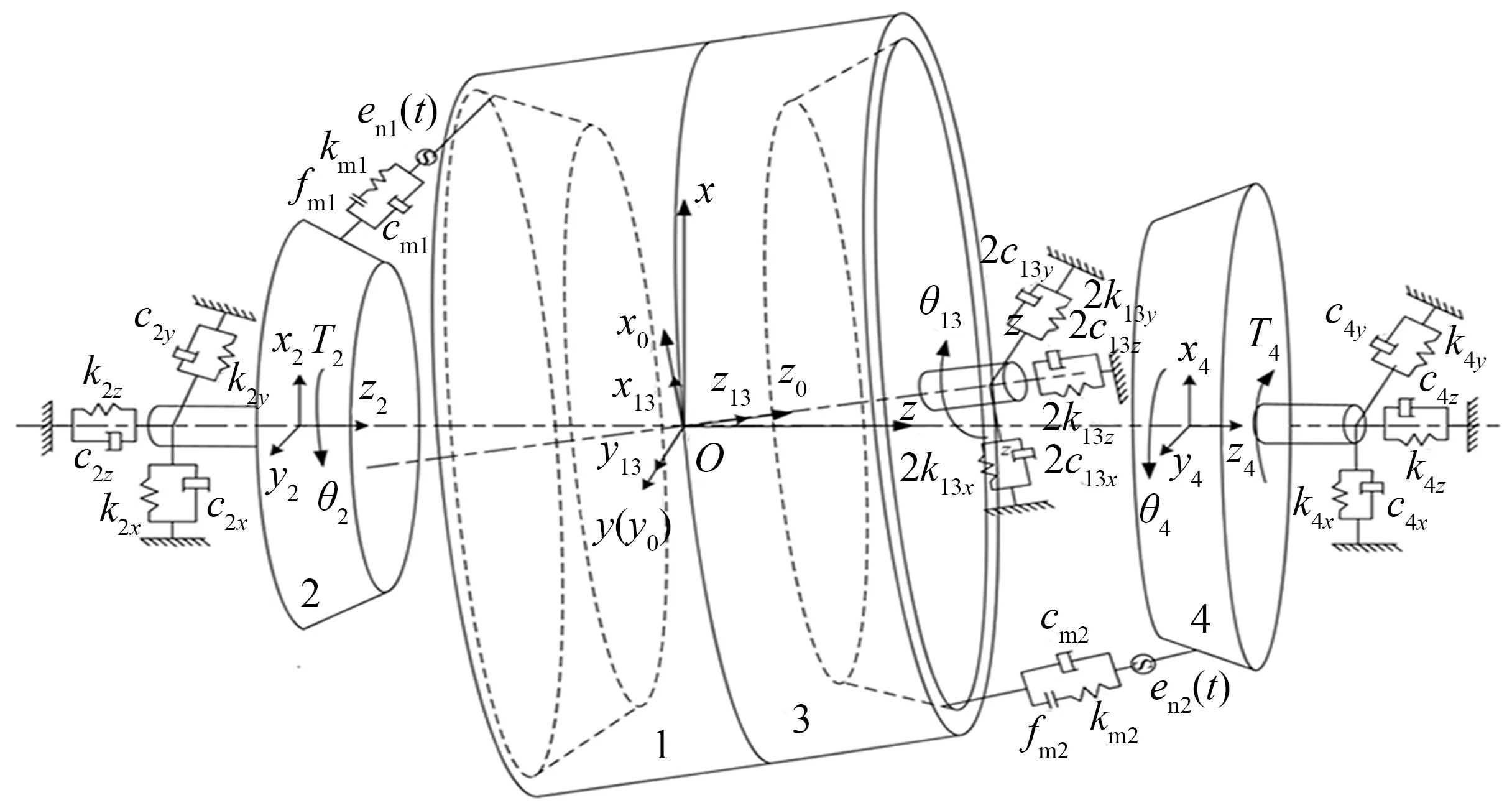
圖2 雙側雙級章動減速器傳動系統動力學模型Fig.2 Dynamic model of two-stage bilateral meshing nutation drive

1.2 系統的激勵分析

齒輪系統的動態激勵有內部激勵和外部激勵兩類.外部激勵主要指來自原動機轉矩或負載的阻力矩作用產生的激勵，包括轉速波動、轉矩波動、幾何偏心等激勵；內部激勵是指齒輪動態嚙合過程產生的激勵，主要包括剛度激勵和誤差激勵.

對于雙圓弧齒形的齒輪，其嚙合剛度定義為所有同時嚙合點單點嚙合剛度的總和,因而它與嚙合點數及嚙合位置有關.雙圓弧螺旋錐齒輪單點嚙合剛度[8]的表達式為

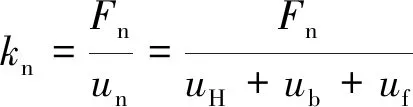
(1)

式中：Fn為作用于單個嚙合點齒面的法向接觸力；un為單個嚙合點處的綜合彈性變形.輪齒的綜合彈性變形包括嚙合點的接觸彈性變形uH、輪齒彎曲產生的輪齒接觸位置的位移ub以及軸承、軸和支撐結構的變形對接觸點變形位置的影響uf.由于uf的量級較小，因此式(1)簡化為：

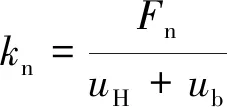
(2)

由于雙圓弧螺旋錐齒輪同時有多個嚙合點接觸，各嚙合點之間是并聯的耦合關系，故齒輪綜合嚙合剛度的表達式為：

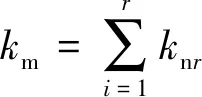
(3)

式中：r為同時接觸的嚙合點數.

雙圓弧螺旋錐齒輪的齒面非常復雜，沿齒長方向上的齒厚是變化的，其綜合嚙合剛度目前沒有解析解.利用有限元軟件ABAQUS建立雙側雙級章動減速器傳動系統有限元模型，如圖3所示，并對其進行加載接觸分析，得到嚙合點處的法向接觸力和彈性變形量，從而計算出齒輪綜合嚙合剛度.為便于求解章動傳動系統非線性動力學模型并盡量模擬真實值，采用8階Fourier級數對綜合嚙合剛度曲線進行擬合，其結果如圖4所示.

圖3 雙圓弧螺旋錐齒輪嚙合剛度Fig.3 Meshing stiffness of double circular arc spiral bevel gears

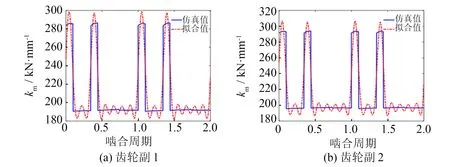
圖4 雙側雙級章動減速器傳動系統有限元模型Fig.4 Finite element model of two-stage bilateral meshing nutation drive

時變嚙合剛度km j的表達式為：

(4)

式中：kav j為齒輪副嚙合剛度的平均值；an j、bn j為諧波項嚙合剛度的幅值；ωm j為齒輪副的嚙合頻率，ωm=2πnz/60，n為各齒輪等效轉速，即將行星輪系轉化為定軸輪系后的轉速.各次諧波參數如表2所示.另外，各級齒輪副嚙合剛度的平均值分別為kav1=210 kN·mm-1，kav2=215.4 kN·mm-1.

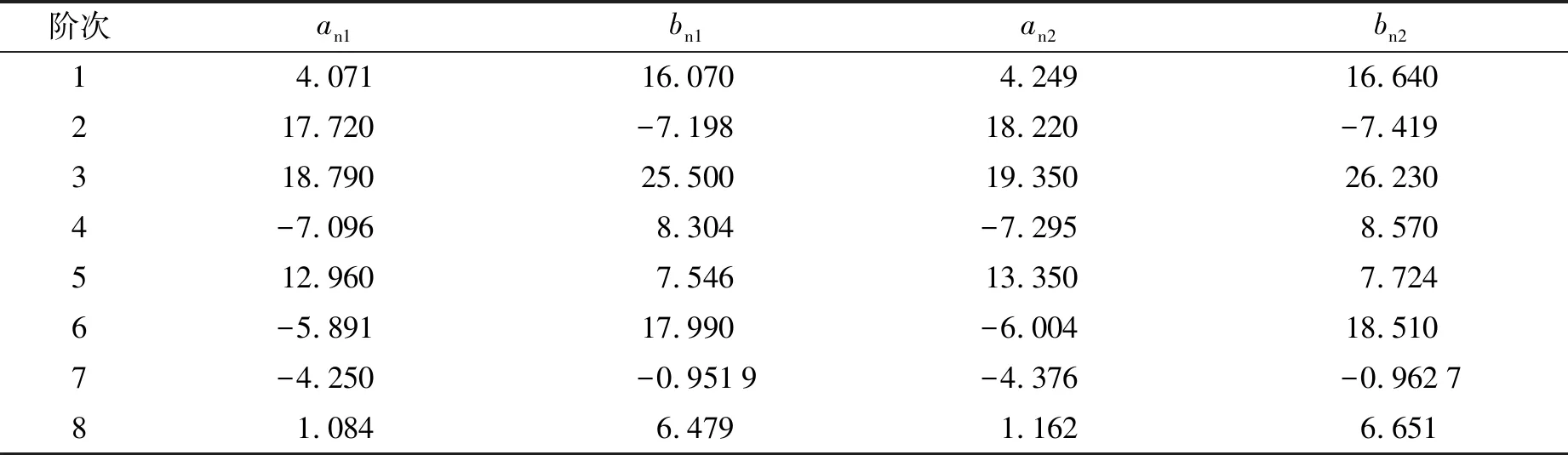
表2 嚙合剛度的各次諧波參數Tab.2 Harmonic parameters of meshing stiffness (kN·mm-1)

齒輪嚙合的靜態傳遞誤差是指實際嚙合位置與理論嚙合位置在嚙合作用線上的差值.各級齒輪副法向靜態傳遞誤差可表示為：en j(t)=er jsin(ωm jt+φj).式中：er j為各級齒輪副法向靜態傳遞誤差幅值.不失一般性，假設減速器為7級精度，參考少齒差行星減速器靜態傳遞誤差[9]，取er j=25 μm；φj為初相位，取φj=0.

1.3 運動微分方程推導

齒輪副在嚙合時的法向動載荷及其沿坐標方向的分力[10]可表示為

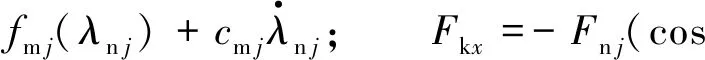
Fky=Fn jcosβcosαn;Fkz=Fn j(sinδksinαn-cosδksinβcosαn)

(5)

式中：λn j(j=1,2)為錐齒輪嚙合過程中因振動和誤差導致嚙合輪齒間產生的動態相對位移；δk(k=1,2,3,4)為各錐齒輪的節錐角;β為螺旋角;αn為法面壓力角.間隙非線性函數表達式為

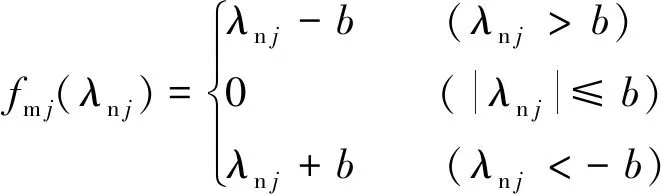
(6)

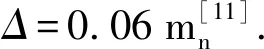
在嚙合力作用下，外錐齒輪2齒面的法向位移xn2可表示為：

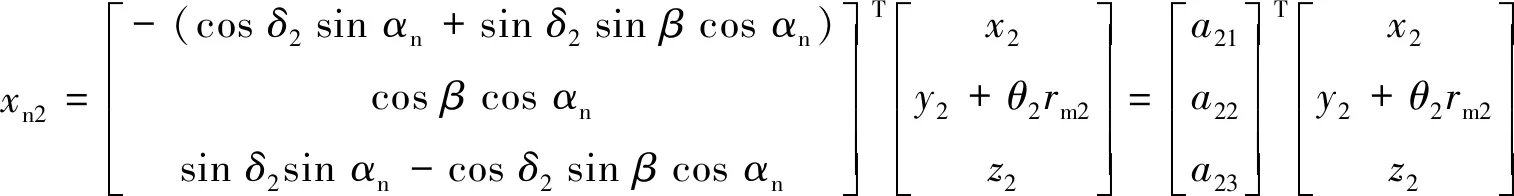
(7)

式中：rm2表示外錐齒輪2嚙合點處半徑，下文中rm1、rm3、rm4含義類似.在實際分析中，取嚙合點半徑為齒寬中點處的回轉半徑[12].

考慮到章動角的影響，章動齒輪1齒面的法向位移xn1可表示為：

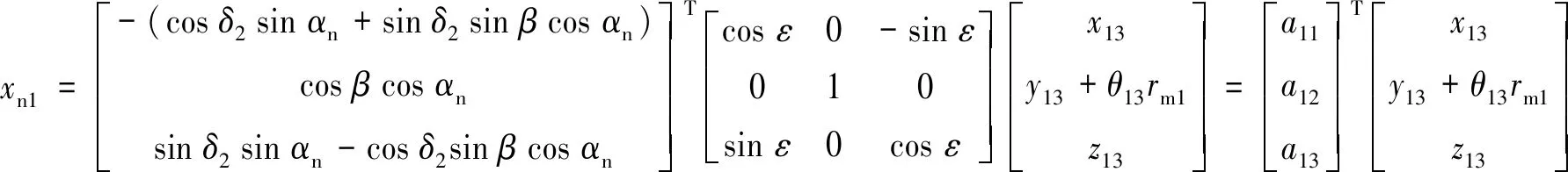
(8)

則第一級齒輪副兩齒輪嚙合過程中由于振動和誤差導致嚙合輪齒間產生的動態相對位移λn1=xn1-xn2-en1(t)；同理可得第二級齒輪副兩齒輪嚙合過程中由于振動和誤差導致嚙合輪齒間產生的動態相對位移λn2=xn3-xn4-en2(t)，其中：

考慮時變嚙合剛度、輪齒誤差、嚙合阻尼、齒側間隙等因素，根據牛頓第二定律，得到章動傳動系統的動力學微分方程如下:

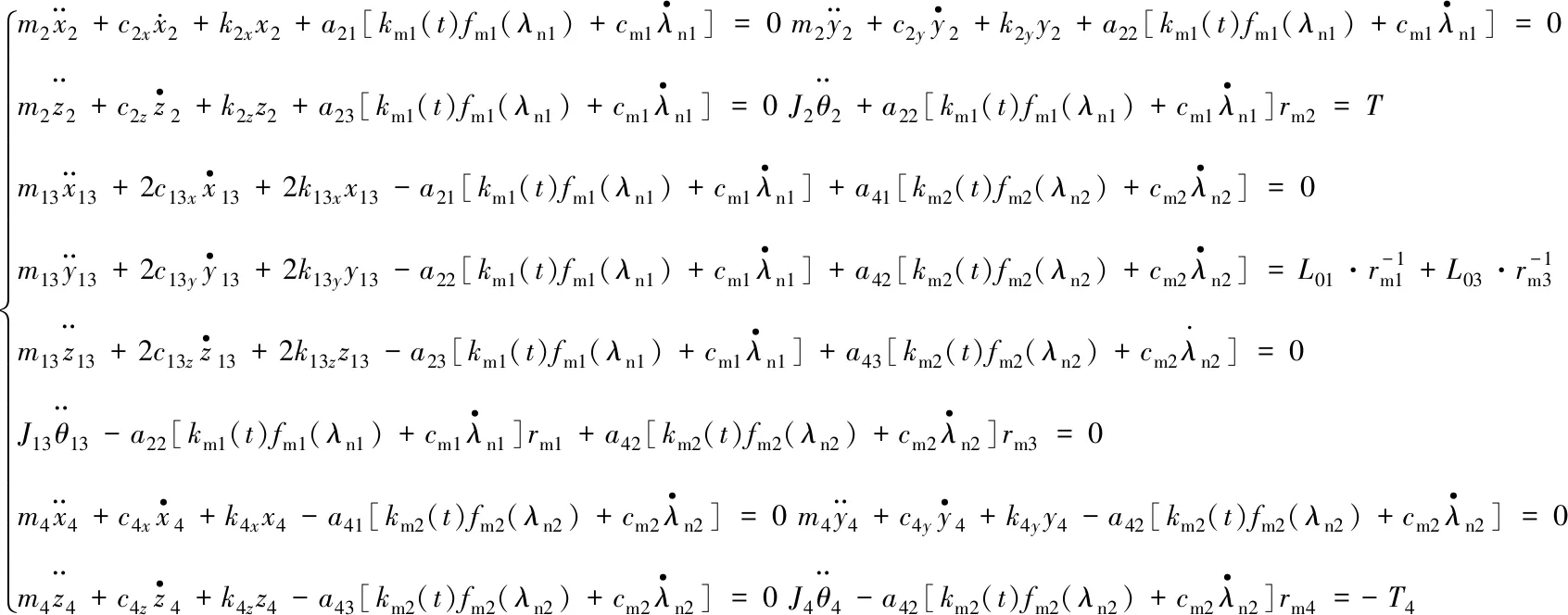
(9)

式中：mi、Ji(i=13,2,4)為各齒輪的集中質量和轉動慣量；L01、L03是兩個內錐齒輪章動運動產生的陀螺力矩，方向沿O-y軸負方向，其通式[13]為

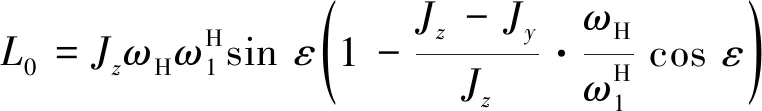
(10)

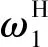
由于齒側間隙的存在，使得齒輪章動傳動系統的約束不完整，章動傳動系統存在剛體位移與不定解.為消除剛體位移，采用λn j消除方程中的θi以實現降維，式(9)第4、8、12個方程可整合為：

式中：mdk(k=1,2,3,4)為各齒輪的等效質量，mdk=Jk/rmk2；md13表示固連齒輪1和3的等效質量，md13=J13/(rm1·rm3).

定義齒輪副的動載荷系數Kj=Fn j/Pn j(j=1,2),式中：Pn j為齒輪副法向靜載荷，Pn1=T1/rm1=T2/rm2，Pn2=T3/rm3=T4/rm4;Tk(k=1,2,3,4)為各齒輪扭矩.

以齒側間隙的一半b為位移標稱尺度，引入相對位移λ1、λ2作為新的自由度，并引入一組無量綱變量其中：取第一級齒輪副的固有頻率ωn為基準頻率，其中：ωn=(kp1/me1)1/2，me1=m2(m1+m3)/(m1+m3+m2).構造系統的無量綱時間τ=ωnt進行歸一化處理，限于篇幅量綱歸一化后的微分方程組這里不再列出.

2 非線性振動特性分析

采用四階Runge-Kutta法求解章動減速器的運動微分方程，取積分時間為500Tm(Tm=2π/Ω，Ω為無量綱激勵頻率，Ω=ωm1/ωn)，舍棄積分初始的200個周期，取后面穩態響應作為系統的動態響應.

已知各齒輪支承剛度分別為：k13x=k13y=k13z=170 kN·mm-1，k2x=k2y=k2z=220 kN·mm-1，k4x=k4y=k4z= 290 kN·mm-1.以第二級齒輪副為例，分析參數對系統動態響應的影響.

2.1 激勵頻率對系統動態性能的影響

齒輪副在不同激勵頻率下的動態響應如圖5所示.隨著激勵頻率的變化，章動傳動系統出現多種振動響應.當Ω=0.9時，系統響應呈現7周期次諧波響應，即周期為7Tm的周期運動，相圖為具有一定寬度的近似橢圓曲線，龐加萊圖呈現7個散點.當Ω=1.9時，相圖為具有一定寬度且交叉纏繞的曲線帶，龐加萊圖呈現7個帶狀點集，系統處于從多周期運動到混沌運動的過渡階段，表明系統在此嚙合頻率下為擬周期運動狀態.當Ω=2.9時，相圖為互相纏繞交叉但不重復的曲線，龐加萊圖呈現有限區域內的點集，表明系統在此嚙合頻率下處于混沌運動狀態.由此可知，隨著激勵頻率的提高，章動傳動系統由多周期狀態經擬周期過渡到混沌狀態，系統非線性特性增強.激勵頻率對動載荷系數的影響如圖6所示.

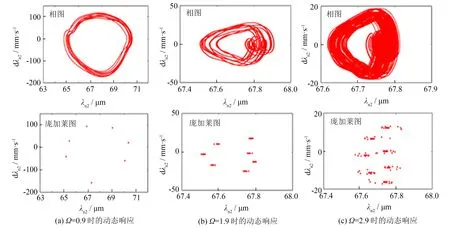
圖5 不同激勵頻率下的動態響應Fig.5 Dynamic response under different excitation frequencies

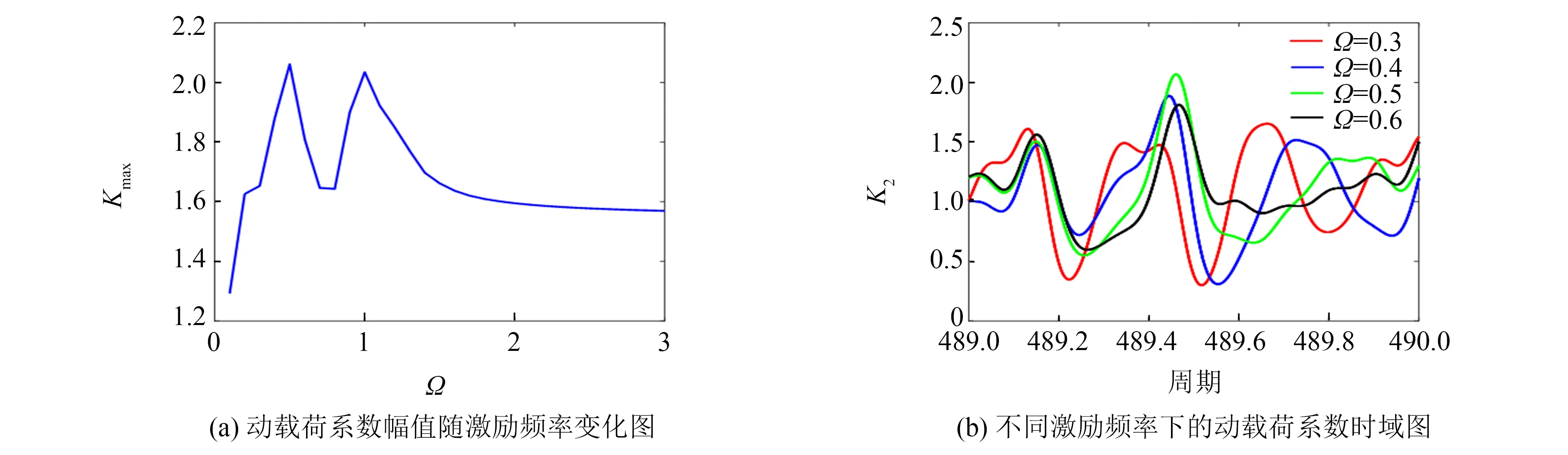
圖6 激勵頻率對動載荷系數的影響Fig.6 Influence of excitation frequency on dynamic load coefficient

圖6(a)為動載荷系數幅值Kmax隨激勵頻率的變化，當無量綱激勵頻率Ω為0.5和1.0時，動載荷系數出現峰值，系統振動最為激烈.圖6(b)為不同激勵頻率下動載荷系數時域圖，當無量綱激勵頻率Ω為0.3～0.5時，動載荷系數幅值隨激勵頻率的增大有顯著增加;但當Ω=0.6時，系統動載荷系數幅值反而下降.類似地，當無量綱激勵頻率在1.0附近時，動載荷系數有同樣的現象，此處不再贅述.因此，通過調節激勵頻率的大小可改善系統的動態特性.

2.2 支承剛度對系統動態性能的影響

章動減速器采用表1中的轉速、轉矩，改變支承剛度，得到不同支承剛度下的動載荷系數，如圖7所示.圖7(a)為動載荷系數幅值Kmax隨支撐剛度的變化.可以看出，當支承剛度倍數為0.5～3.5時，章動減速器動載荷系數幅值隨支承剛度的增加而顯著降低；當支承剛度倍數為3.5～7.0時，系統動載荷系數幅值隨支承剛度的增加逐漸增大；當支承剛度倍數大于7時，動載荷系數幅值基本不變.圖7(b)為不同支承剛度下的動載荷系數時域圖.可以看出，當支承剛度倍數由1增大到3.5時，動載荷系數幅值及變化幅度均逐漸減小;當支承剛度倍數由3.5增大到5.0時，動載荷系數幅值反而增大.因此，適當增大支承剛度可以降低系統的動載荷系數，提高章動傳動系統的穩定性.

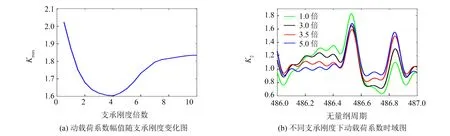
圖7 支承剛度對動載荷系數的影響Fig.7 Influence of support stiffness on dynamic load factor

3 動力學模型驗證

為驗證動力學建模的正確性，將由集中參數法求得的動態嚙合力與用ADAMS仿真得到的法向嚙合力進行對比.不失一般性，假設工況均為輸入轉速1 050 r·min-1、輸出轉速10 r·min-1、輸出轉矩170 N·m，由微分方程(9)求得的動態嚙合力如圖8所示.ADAMS仿真求解得到的齒輪法向嚙合力詳見文[7].

由集中參數法求得的兩級齒輪副穩態響應下動態嚙合力均值分別為5 877、5 628 N，由ADAMS仿真求得的兩級齒輪副穩態響應下嚙合力均值分別為6 074、5 885 N，嚙合力均值最高僅相差4.37%.集中參數法求得的嚙合力波動較大,主要是由于考慮了時變嚙合剛度.在ADMAS中計算碰撞力時剛度系數為定值，表明采用集中參數法更能反映動態嚙合力的時變性，從而驗證了本彎-扭耦合動力學模型的正確性.

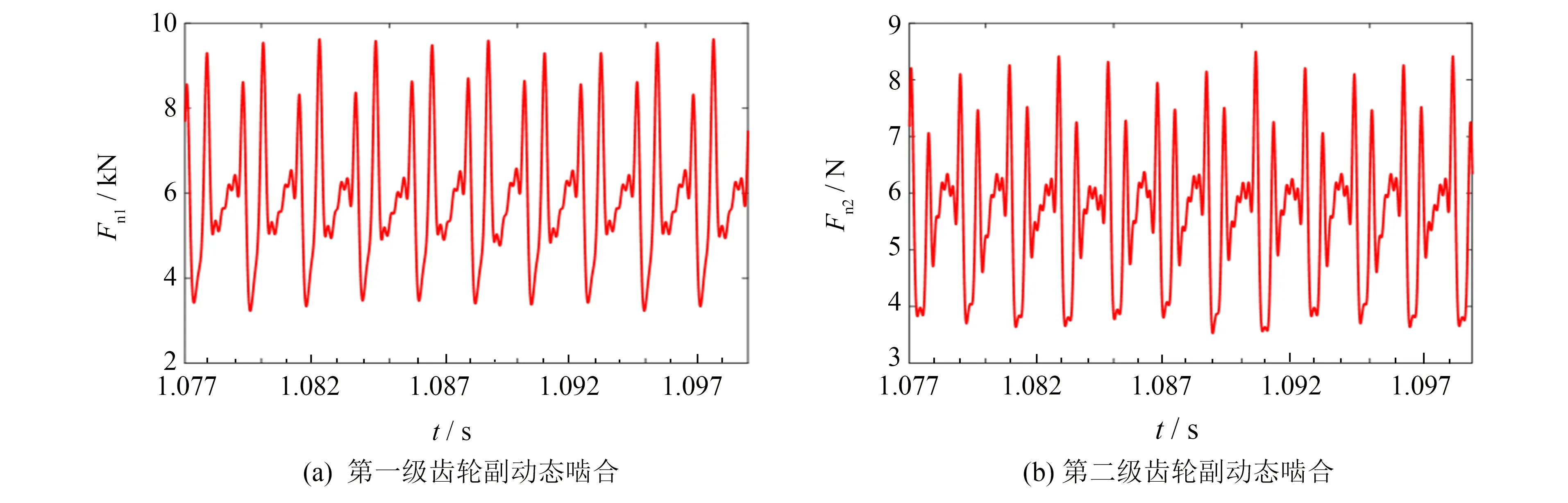
圖8 集中參數法求得的齒輪動態嚙合力Fig.8 Gear dynamic meshing force obtained by the lumped parameter method

4 結語

1)計入時變嚙合剛度、嚙合阻尼、傳遞誤差、齒側間隙等因素，建立了雙側雙級雙圓弧螺旋錐齒輪章動減速器彎-扭耦合非線性動力學模型.

2)隨著激勵頻率的增大，系統相繼呈現3類穩態響應：7周期次諧響應、擬周期響應、混沌響應.當無量綱激勵頻率等于0.5和1.0時，動載荷系數出現峰值，系統振動最為激烈.適當調節激勵頻率的大小可以改善系統的動態穩定性.

3)在支承剛度的0.5～3.5倍范圍內，系統動載荷系數隨著支承剛度的增加而降低.適當增大支承剛度可以降低章動傳動系統的動載荷系數，提高章動傳動系統的穩定性.為后續章動傳動系統動態優化設計提供一定的理論依據.

4)通過對比本模型所求解的動態嚙合力與用ADAMS軟件仿真求得的法向嚙合力，發現嚙合力均值最高僅相差4.37%，驗證了本彎-扭耦合非線性動力學模型的正確性.