屈曲約束支撐核心構件幾何參數對支撐受力性能影響分析

陳凌秀，祁 皚

(福州大學土木學院,福建 福州 350108)

0 引言

屈曲約束支撐(buckling-restrained brace,BRB)是一種耗能優良的支撐構件，許多工程將支撐運用于框架，組成屈曲約束支撐框架(buckling-restrained brace frame，BRBF).

支撐內部構件分為核心段、轉換段、連接段3個部分，其中核心段長度的取值對BRB的屈服時機以及BRB的滯回性能具有十分重要的影響，直接影響BRB的能量耗散.核心段長度太短，結構變形時，其應變將會超出支撐的極限應變，使BRB發生損壞導致框架嚴重破壞，核心段長度太長會使支撐晚于框架屈服，起不到保護框架的作用.因此選擇合理的核心段長度對支撐設計尤為重要，蔡克銓等[1]探討了具有不同核心段長度BRB的試驗性能，認為可通過調整BRB核心段長度來控制其屈服消能的時機，越短的核心段長度，框架層間位移角越小時就能屈服耗能；Mirtaheri等[2]研究了不同核心段長度對BRB耗能的影響，核心段長度越短，耗能越好，但疲勞對其性能的影響也越大；伊文漢等[3]考慮疲勞破壞對核心段長度的影響提出BRB最小核心段長度的計算方法；李國強等[4]認為可通過選擇較小的核心段長度和較低屈服點的鋼材，確保支撐先于框架發生破壞，但核心段長度不宜小于BRB工作長度的0.4倍.Hoveidae等[5]考慮材料低周疲勞、強度、以及幾何尺寸等因素，建議BRB核心段長度最小值取為其工作長度的15%～25%；Pandikkadavath等[6]研究利用有限元軟件分析了不同核心段長度BRB的滯回耗能，并著重分析短的屈曲約束支撐框架(frame fitted with BRBs of short core lengths,SBRBF))的非線性動力性能，結果表明，減小BRB核心段長度有利于減小地震反應下框架結構的層間位移角；孫治國[7]、石巖[8]推導了BRB用于橋梁結構時，核心段長度范圍的表達式.目前針對BRB核心段長度的研究主要集中在對其最小長度的研究，對其最大取值范圍的研究較少，本文通過作者推導的考慮節點板剛度的核心段應變計算公式以及有限元模擬分析，深入分析核心段幾何參數對支撐力學性能的影響，并根據分析結果，給出核心段長度的合理取值范圍.

1 屈曲約束支撐核心應變計算公式

作者推導了考慮與BRB焊接連接的節點板剛度，支撐核心段應變表達式[9]如下：

(1)

βc=0.564+0.668μc-95.172α-0.307μc2+3 201.55α2

(2)

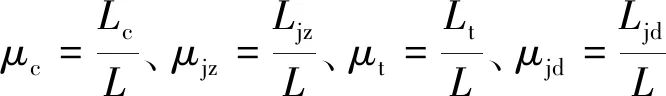
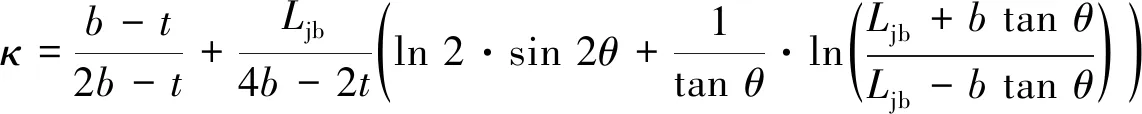
(3)

式(3)中b、t分別為節點板1-1截面的長度和厚度，如圖2所示.

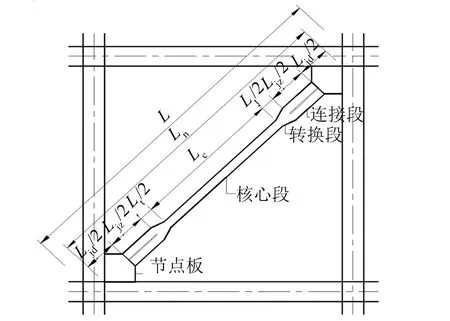
圖1 屈曲約束支撐的剛度串聯示意圖Fig.1 The series connection of BRBS

圖2 約束屈曲支撐框架節點板構造圖Fig.2 Configurations of BRB-gusset plates

公式(1)的結果已與足尺屈曲約束支撐框架的擬靜力試驗和框架實體有限元分析進行對比，三者結果吻合較好.對公式(1)進行誤差分析，結果表明公式用于計算支撐屈服時的層間位移角可以減少60%以上的誤差，并可用于支撐核心構件的優化設計.

公式(1)的參數中，對于一個給定的框架，屈曲約束支撐的軸力設計值一旦確定，μjd、μjz、μt、γjd是定值，因此只有μc、γt、γjz這三個參數可以變化.從公式(1)可看出，屈曲約束支撐可由軸向各分段面積比例及核心段長度的調整來構成所需剛度及屈服消能時機.以下分別討論這些參數對支撐力學性能的影響.

2 公式各參數對支撐受力的影響

2.1 支撐屈服時公式各參數的影響

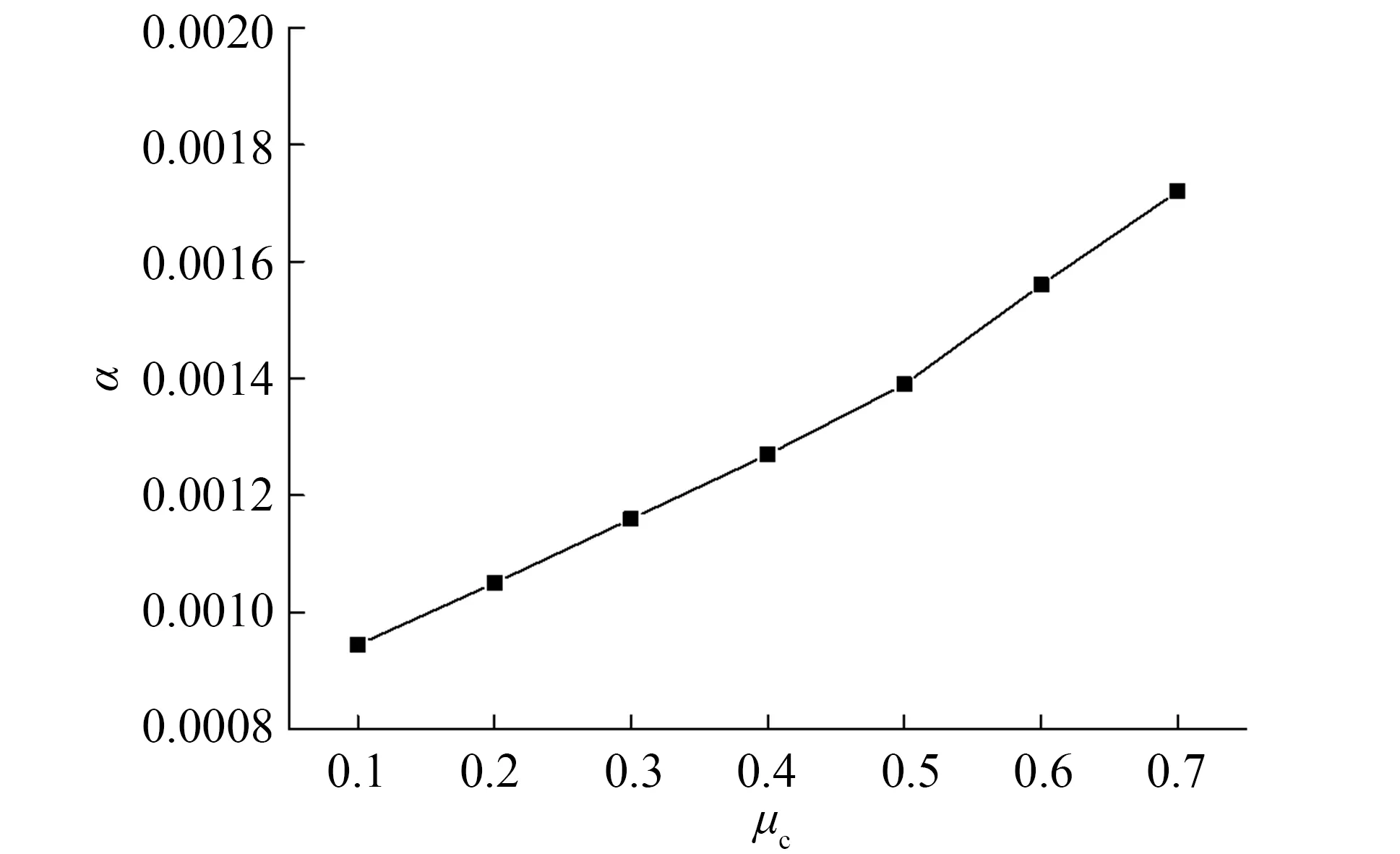
圖3 支撐屈服時框架層間位移角α隨μc變化圖Fig.3 Inter-story drift of BRBS during yielding for various μc

對于235鋼，支撐屈服應變的理論值為0.11%，將支撐屈服應變值代入式(1)中，可計算出支撐發生屈服時框架的層間位移角，保持γjz、γt值不變，變化μc值得到支撐屈服時框架所發生的層間位移角α與μc的關系圖，如圖3所示.從圖3中可看出，隨著μc值的增大，支撐發生屈服時所需的框架層間位移角α逐漸增大，即μc值越大，支撐越晚屈服.

圖4(a)為保持γjz值不變，支撐屈服時框架所發生的層間位移角α隨μc、γt變化關系圖.從圖中可看出，對于同一μc值，隨著γt值的增大，支撐發生屈服時所需的框架層間位移角α逐漸減小，即γt值越大，支撐越早屈服.這是由于在轉換段長度不變的情況下，轉換段和連接段的總剛度隨著面積的增大而增大，核心段的變形也隨之增大，支撐越早屈服.γt值在1.5～2.0之間變化時，α角減小的較為明顯.當μc<0.5時，γt對支撐進入屈服早晚的影響很大，μc≥0.5時，γt對支撐進入屈服早晚的影響小，可以忽略.這主要是由轉換段和核心段的剛度比決定的，支撐的軸力設計值一旦確定，連接段的長度就確定了，μc值越小，則轉換段的長度就越長，轉換段和連接段的總剛度就隨之減小，當總剛度減小到一定范圍時，剛度變化對核心段的變形影響就開始變得明顯.當μc等于0.5時，變化γt，所得到的轉換段和核心段的剛度比最小值為9，當轉換段和核心段的剛度比小于9時，剛度變化對核心段的變形影響趨于明顯，此時不能忽略γt對支撐進入屈服早晚的影響.

圖4(b)為保持γt值不變，支撐屈服時框架所發生的位移角α隨支撐μc、γjz變化關系圖.從圖中可看出，對于同一μc值，隨著γjz值的增大，支撐發生屈服時所需的框架層間位移角α有所減小，即γjz值越大，支撐越早屈服，但跟μc值對α的影響相比，γjz值對其的影響不十分明顯，因此可忽略γjz對支撐屈服時所需的層間位移角的影響.

由圖4知，當μc=0.7時，支撐屈服所需的層間位移角α接近鋼筋混凝土框架的彈性層間位移角限制(1/550)，若μc>0.7，α將大于1/550時，混凝土結構已經超過其彈性位移角限值，支撐還未屈服.

圖4 支撐屈服時層間位移角α隨參數變化圖Fig.4 Inter-story drift of BRBS during yielding for various parameters

2.2 支撐屈服后各參數的影響

圖5為層間位移角等于1/50時，γt=2.0，γjz=4.0時支撐應變隨μc的變化圖.從圖中可看出，支撐的平均應變隨著μc的增大而減小，這是因為在相同層間位移下，支撐的軸向變形是一致的，支撐平均應變隨著核心段長度的增加而減小.

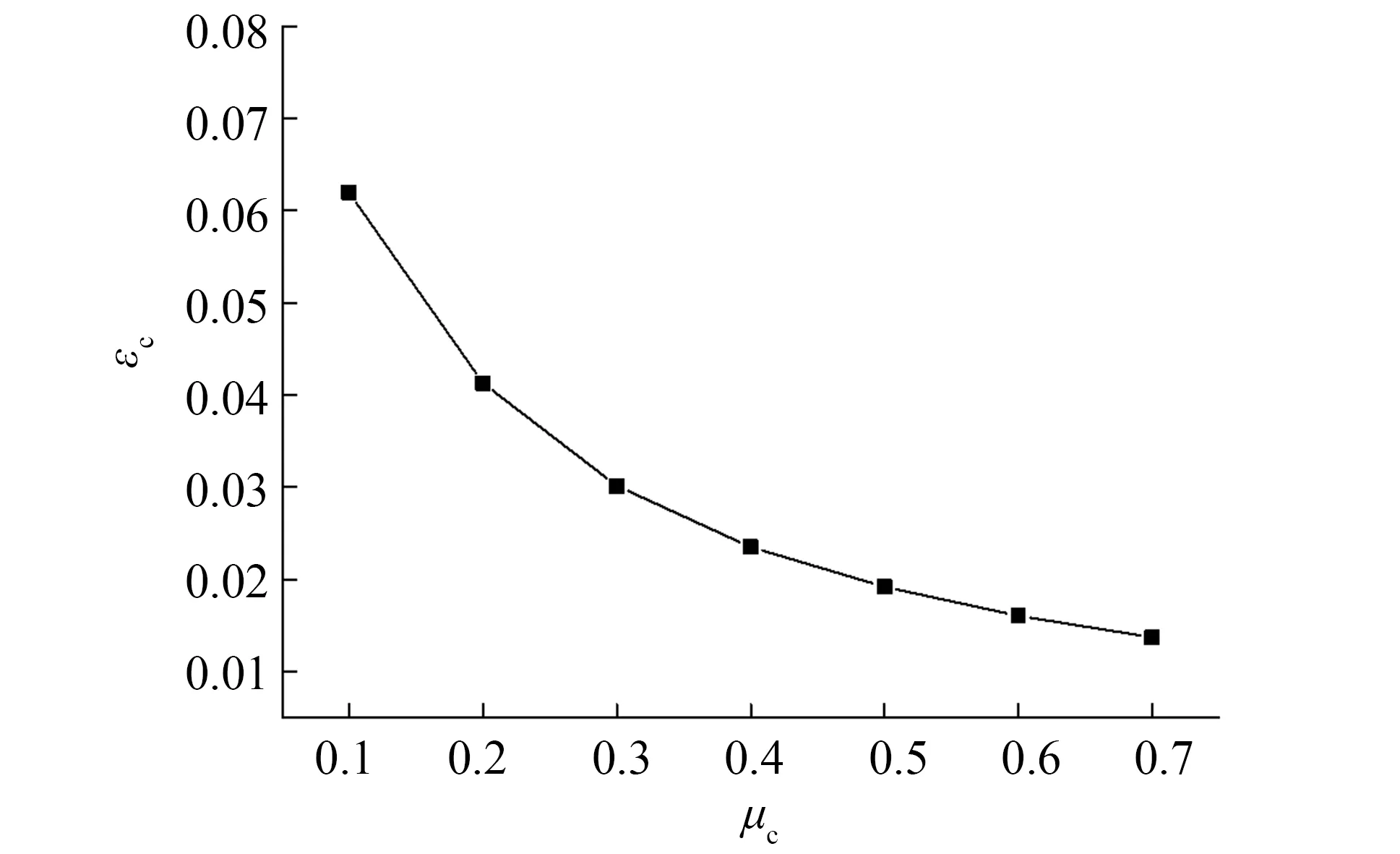
圖5 支撐核心段應變隨μc變化圖Fig.5 Core strain for various μc

圖6(a)為保持γjz不變，支撐核心段應變隨μc、γt變化圖.圖6(b)為γt保持不變，支撐核心段應變隨μc、γjz變化圖.從圖6(a)可看出，在相同的μc下，支撐應變隨著γt的減小而減小，當μc<0.2時，應變隨著γt減小的較為明顯.當μc≥0.2時，可以忽略γt的變化對支撐應變值的影響.從圖6(b)可以看出在相同的μc下，支撐應變隨著γjz的減小而減小，但減小幅度很小，可以忽略γjz對屈服后支撐應變的影響.

從圖6中還可看出,當μc小于等于0.3時，當框架層間位移角達到1/50時，支撐的核心應變將大于3%，文獻[6,10-12]認為，屈曲約束支撐核心段應變小于3% 時，能夠保持穩定的力學行為，因此在進行屈曲約束支撐設計時，μc的取值不能太小，應大于0.3.

圖6 支撐核心段應變隨參數變化圖Fig.6 Core strain for various parameters

3 有限元分析

3.1 有限元模型介紹

用ANSYS分析軟件建立屈曲約束支撐框架的實體有限元模型，模型的單元材料特性見表1，約束屈曲支撐內核和外包混凝土之間設置接觸對，分別采用Targe170目標單元和Conta173接觸單元.BRB與框架結構節點板之間的連接為焊接，建模時直接將節點板與BRB之間通過共用的節點連接.該有限元模型已通過足尺BRBF擬靜力試驗證明了有限元模型的正確性.支撐內核單元的本構關系采用雙線性彈塑性模型，屈服后支撐剛度為屈服前的0.02倍，如圖7所示.屈曲約束支撐框架實體模型如圖8所示.

表1 單元材料特性表Tab.1 Element material property sheet

圖7 支撐內核本構關系圖Fig.7 Constitutional relationship of core steel

圖8 屈曲約束支撐框架實體模型圖Fig.8 Solid model of the BRBF

3.2 有限元參數分析

在進行屈曲約束支撐設計時，支撐軸力設計值一旦確定，μjd、μjz是定值，對于大多數支撐而言，轉換段和核心段的面積比γt一般取值在1.5～2.0之間，連接段和核心段的面積比γjz一般取值為4，可變化的范圍不大；支撐核心段長度的設置則可以通過調整轉換段的長度來實現，變化范圍比較大，對支撐受力性能的影響較大，下面以實體有限元模型為基礎，研究支撐核心段與支撐兩工作點間總長的比值μc對支撐受力性能的影響.

3.2.1支撐μc值對支撐單軸受力性能的影響

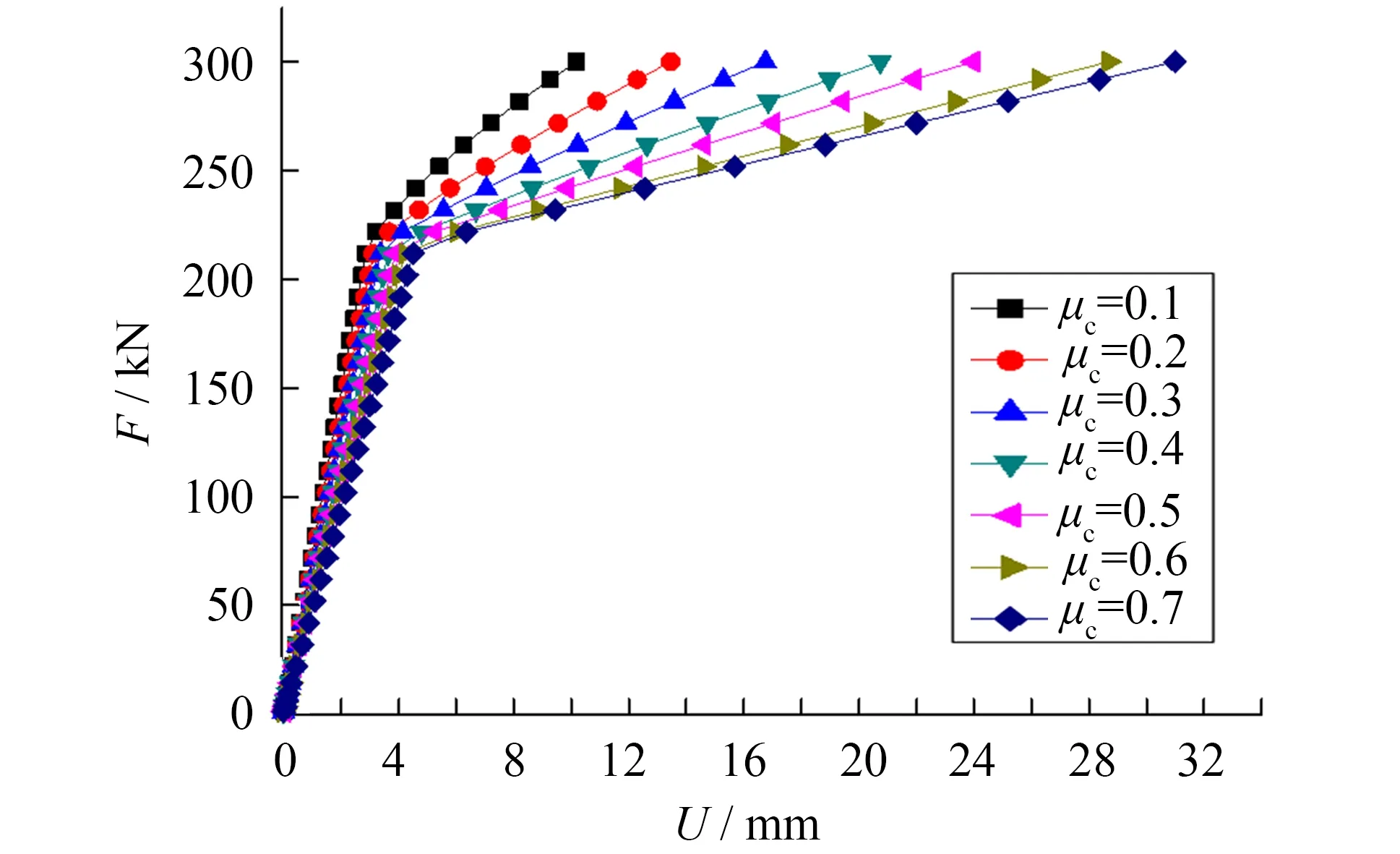
圖9 支撐單軸力位移曲線隨μc變化圖Fig.9 Relationships between force and displacement for various μc of BRBS

通過改變有限元模型中支撐核心段長度，得到不同的μc值，分別為0.1、0.2、0.3、0.4、0.5、0.6、0.7，研究不同的μc值對支撐的單軸受力性能的影響如圖9所示.從圖9可看出，隨著μc的增大，支撐越晚發生屈服，且屈服后支撐的剛度也減小的更多，支撐變形更加明顯，變化趨勢與文獻[6]的有限元模擬結果相吻合.

3.2.2支撐μc值對支撐滯回性能的影響

通過改變有限元模型中支撐核心段長度，得到不同的μc值，分別為0.1、0.3、0.5、0.7，不同的μc值對支撐滯回性能的影響.

圖10為當框架層間位移角達到1/50時，核心段受壓變形圖.當μc=0.1時，變形為平面內的側移，當μc≥0.3時開始出現平面外的正弦波變形，此時核心段將會與外包混凝土相接觸，且隨著μc的增大，波數越多，核心段的變形特點與文獻[13]中試驗及有限元模擬的結果吻合.

圖10 支撐核心段變形圖Fig.10 The deformation of the core segment

圖11為支撐核心段端部應力應變隨μc的變化圖.從圖11可看出，支撐的耗能能力隨著μc的增大而減小；隨著μc的增大，支撐端部應力應變滯回曲線的拉壓不對稱性越來越明顯，當μc=0.5時，支撐核心段端部的滯回曲線拉壓不對稱性明顯，當μc=0.7時，支撐核心段端部的滯回曲線不但拉壓不對稱性，而且隨著位移角的增大，滯回環所包圍的面積也在減小，支撐端部耗能能力開始下降.這是因為支撐核心段端部的不僅僅受到軸力的作用，還要承受一定的彎矩[14]，支撐的核心段越細長，在軸力和彎矩的共同作用下，這種的拉壓不對稱性會越明顯.因此為了保證支撐在承受往復荷載時的穩定性，μc的取值不宜太大，若支撐采用螺栓連接，還需考慮一定的連接段長度，建議μc≤0.7.

圖11 支撐核心段端部應力應變滯回曲線隨μc變化圖Fig.11 Hysteresis loop for various μc on the end of the core segment

4 結語

1)支撐核心段長度與兩工作點間總長的比值μc對其屈服消能時機影響很大，μc越小，越早進入屈服，μc越大，越晚進入屈服.

2)支撐屈服前，屈服消能時機不僅跟μc值有關，還跟轉換段與核心段面積比有關；面積比值越大，支撐越早屈服.支撐屈服后，可以忽略支撐內核各段的面積比對其應變的影響，只考慮μc對應變的影響

3)μc對支撐的滯回性能影響較大，隨著μc的減小，耗能能力增大.

4)為保證支撐穩定的力學性能，μc的合理取值范圍建議在0.3～0.7.