基于加速老化和實測載荷的立式貯存固體發動機藥柱壽命評估

王鑫， 趙汝巖， 盧洪義， 劉磊， 伍鵬

(1.海軍航空大學， 山東 煙臺 264001; 2.南昌航空大學， 江西 南昌 330063)

0 引言

固體發動機壽命主要取決于藥柱的貯存壽命，開展藥柱壽命評估研究對于確保導彈可靠性和正常發射具有十分重要意義[1]。國內外各國都非常注重發動機貯存壽命的研究與評估工作，以美國為例，早在20世紀70年代，美國就針對老化趨勢制定了長期監測計劃，并于21世紀初探索監測與數值仿真技術相結合，試圖實現壽命的在線分析[2-3]。同時國內外也有大量學者對推進劑壽命進行了研究，多以加速老化試驗為主。Michael[4]和Bilgin等[5]分別從溫度和濕度角度出發，開展不同條件下的老化試驗，建立了老化程度與推進劑貯存溫度之間的關系，測試了推進劑的力學性能。傅惠民等[6]和陳海建等[7]在傳統Arrhenius公式基礎上，分別提出改進方法，提高了預估精度。張曉軍等[8]對發動機粘接界面進行了加速老化試驗，測試了粘接界面的扯離強度，預測了發動機使用壽命。

以上推進劑壽命預估研究大都是通過加速老化試驗，并沒有考慮發動機實際承載過程，對于載荷經歷越復雜的發動機，其壽命預估結果將越不準確。基于此，袁端才等[9]、謝振波等[10]和楊繼坤等[11]相繼開展了推進劑加速老化試驗和不同貯存期的發動機點火發射過程數值仿真，基于獲得的延伸率和應變隨時間變化規律進行對比分析，得到了發動機貯存壽命。唐國金等[12]和高鳴等[13]進行了發動機常溫點火發射下的響應面隨機有限元分析，并利用應力- 強度干涉模型得到了可靠度與貯存時間的關系，進而獲取發動機壽命。與此同時，Yilmaz等[14]考慮長時貯存和公路運輸的影響，采用響應面法建立了應力- 應變的替代數學模型，計算了某置信區間內的瞬時可靠性。王永帥等[15]和張波等[16]還針對艦載立式貯存固體發動機藥柱和粘接界面的蠕變和疲勞損傷分別展開了研究，為艦載發動機壽命評估提供了一定依據。

但上述文獻未對發動機前期貯存歷程展開研究，或者考慮并不全面。對于固體發動機而言，其全壽命周期需經受固化降溫、公路運輸、臥式貯存和戰備值班以及最終的點火發射過程，固化降溫使發動機藥柱產生不可忽視的預應力和預應變，公路運輸產生的隨機振動載荷使藥柱產生累積損傷，戰備值班長時立式貯存以及周期性的低頻振動載荷會使藥柱產生不可恢復的蠕變與疲勞損傷，這些因素都將影響后續的點火發射，也影響著發動機壽命。

本文忽略臥式貯存及公路運輸載荷的影響，并在通過高溫加速老化試驗獲取延伸率隨時間變化規律的基礎上，開展不同貯存期發動機經固化降溫、立式貯存及點火發射的數值仿真，獲取點火增壓和彈射過載聯合作用下的藥柱最大von Mises應變。同時開展實測振動載荷下發動機的有限元分析，計算發動機動態立式貯存半年時間的疲勞損傷。進而通過延伸率和應變的變化規律，結合疲勞損傷值預估貯存溫度下發動機壽命，并得到了發動機前期貯存時間與動態立式貯存次數的關系式。

1 加速老化試驗

本文所選材料為某型固體火箭發動機藥柱所用的端羥基聚丁二烯(HTPB)復合推進劑。根據航天工業部標準QJ2328A—2005《復合固體推進劑高溫加速老化試驗方法》、QJ1615—89《復合固體推進劑單向拉伸試驗方法》以及QJ2487—93《復合固體推進劑單向拉伸應力松弛試驗及主曲線測定方法》，選取50 ℃、60 ℃和70 ℃ 3個溫度進行加速老化試驗，選取不同測點獲取推進劑各參數隨老化時間的變化規律。

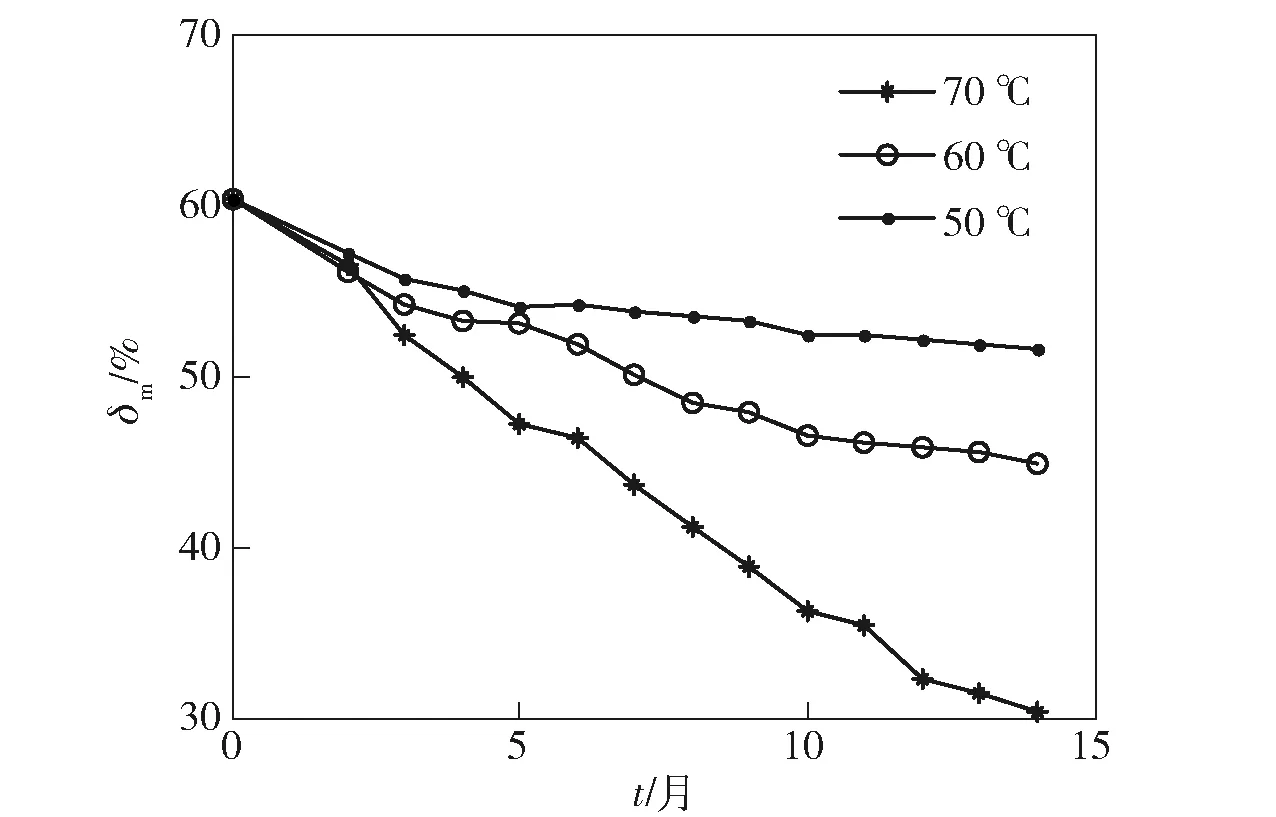
圖1 最大延伸率變化趨勢Fig.1 Changing curves of maximum extensibility

最大延伸率δm和最大抗拉強度σm結果如圖1和圖2所示，其中t為老化時間。由圖1和圖2可見：隨著老化時間增加，推進劑逐漸變硬，呈現抗拉強度和模量不斷增加，延伸率不斷減小的趨勢；同時隨著溫度升高，變化趨勢加快。

圖2 最大抗拉強度變化趨勢Fig.2 Changing curves of maximum tensile strength

通常，加速老化性能δm隨時間的變化規律可用以下3種模型進行表示，其分別記作模型1、模型2和模型3.

δm=δ0+Klgt,

(1)

δm=δ0+Kt,

(2)

δm=δ0exp (-Kt),

(3)

式中：δ0為常數；

K=Zexp (-E/(RT))，

(4)

Z為頻率因子，E為表觀活化能，R為氣體常數，T為熱力學溫度。

表1列出了試驗數據對各模型的擬合結果，其中δ1、δ2和δ3以及K1、K2和K3為擬合參數，r1、r2和r3為相關系數。

表1 各模型擬合結果

由表1可知，3個模型擬合結果都比較好，故選用較為簡單的線性模型作為最終擬合結果。根據《復合固體推進劑高溫加速老化試驗方法》標準中數據處理方法，通過(2)式和(4)式推導出貯存溫度Ts(Ts=20 ℃)條件下推進劑最大延伸率δm的變化規律為

δm=60.4-exp (29.633 3-9 361/Ts)×t.

(5)

2 三維有限元分析

2.1 模型建立及材料參數

某型固體發動機藥柱為帶有前后人工脫粘層的前后翼槽結構，具有幾何對稱性，模型結構及網格劃分如圖3所示。

圖3 發動機模型結構及網格劃分Fig.3 Structure and mesh generation of motor model

通過推進劑松弛試驗獲取其松弛模量E(t)主曲線，并用Prony級數形式表示，僅給出未老化推進劑在20 ℃下松弛模量主曲線表達式，如(6)式所示，老化試件松弛模量獲取方法同未老化試件。同時將各部件主要參數列于表2中。

E(t)=1.037+3.26e-t/0.04+2.068e-t/0.4+1.284e-t/4+
0.891e-t/40+0.587e-t/400+0.43e-t/400+0.316e-t/40 000.

(6)

表2 各部件材料參數

2.2 邊界及載荷處理

在仿真過程中主要考慮固化降溫載荷、立式貯存載荷以及點火發射與彈射增壓載荷，忽略其他載荷對發動機壽命的影響，并分別開展以下工況的有限元仿真，工況如表3所示。其中：工況1的運算可以獲取藥柱經聯合載荷作用下的最大von Mises應變發生位置；通過工況2中對立式貯存時間(立式貯存次數)的調整，探尋貯存壽命與立式貯存次數之間的關系；通過工況3計算藥柱在立式振動載荷條件下的疲勞損傷，最終得出發動機經表3所示5種載荷綜合作用下的貯存壽命。

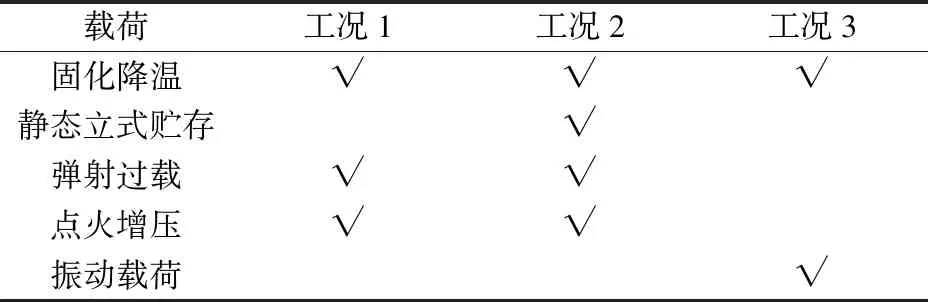
表3 各工況對應載荷歷程

在工程模擬有限元軟件Abaqus中，通過設置多個分析步來實現不同工況下聯合載荷的仿真計算，且后一載荷工況在前一載荷的仿真結果基礎上進行，并通過改變藥柱模量參數來實現推進劑老化因素的關聯。

表3中：固化降溫過程的0應力溫度為50 ℃，經過一段時間降至室溫；靜態立式貯存過程中恒定承受1g的重力載荷，長時立式貯存時對藥柱施加前期擬合的蠕變參數，即

(7)

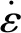
同時為簡便計算，將彈射過載與點火增壓載荷認定為線性載荷；振動載荷采用實際監測數據，選取具有代表性的100 s進行計算。前兩種工況由于邊界及載荷的對稱性，仿真對象選用1/16模型；由于工況3中振動載荷由橫搖、縱搖及垂蕩3個方向的加速度共同決定，仿真對象選用全尺寸模型。

令ax、ay和az分別表示垂蕩、橫搖及縱搖3個方向的加速度，圖4所示為經數據處理后的各方向加速度隨時間變化曲線，其中ta為加速度振動載荷采集時間。

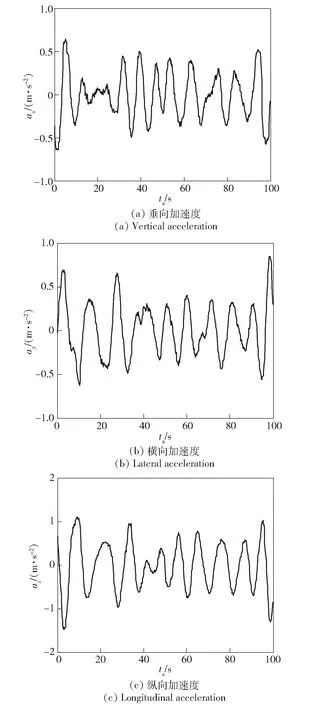
圖4 3個方向實測加速度曲線Fig.4 Accelerations in three directions

2.3 仿真結果及分析

2.3.1 立式貯存

對未老化發動機的三維數值仿真結果表明：經固化降溫載荷后，在熱應力作用下，藥柱前后人工脫粘層張開，藥柱中孔擴張，藥柱內部產生初始預應力與預應變；在立式貯存初期，在1g軸向重力載荷作用下，藥柱前人工脫粘層繼續擴張，后人工脫粘層開口距離減少，藥柱整體有向尾部下沉的趨勢；經長期靜態立式貯存載荷后，藥柱整體下沉量增大，最大位移值增大了14.82%，后人工脫粘層縫隙逐漸減小，表明藥柱在長期立式貯存下會產生蠕變。發動機藥柱在不同載荷下的位移歷程如圖5所示。由圖5可見，由于位移變化占據發動機總長的比例較小，故為清晰看清藥柱在各階段變形趨勢，圖5為放大15倍之后的結果。

圖5 立式貯存下不同階段位移變化云圖Fig.5 Displacement nephograms at different phases during vertical storage

圖6為長時立式貯存后的藥柱應變云圖，最大應變發生在藥柱前翼與中孔交匯位置，可達0.042 37.

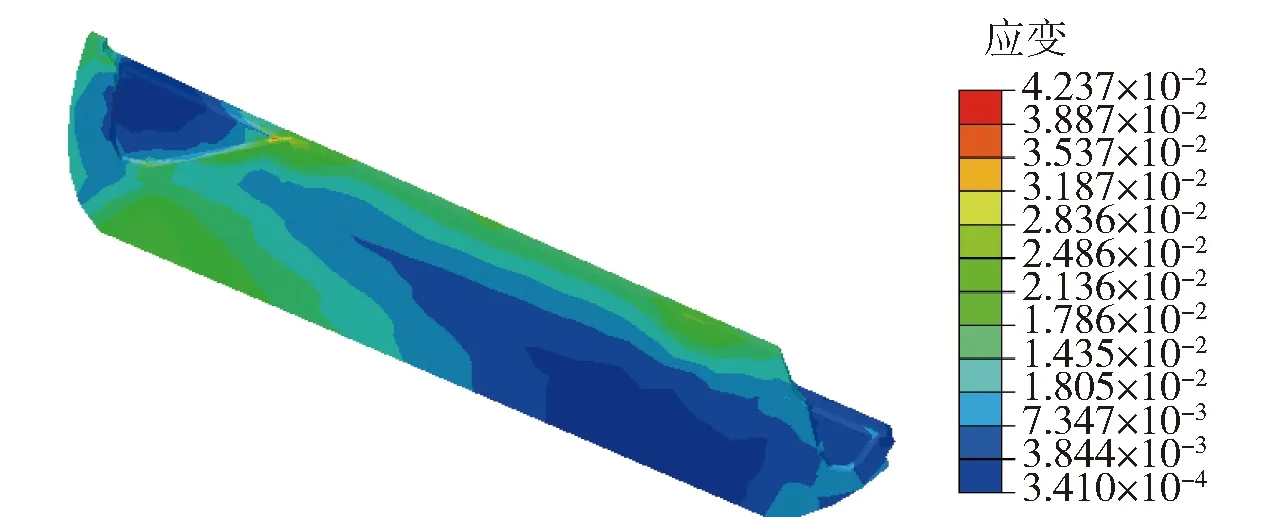
圖6 長時立式貯存后應變云圖Fig.6 Strain nephogram after long-time vertical storage

2.3.2 點火增壓和彈射過載

在遠大于重力加速度的彈射過載和點火增壓載荷聯合作用下，藥柱前后人工脫粘層與前后封頭貼緊，位移分布如圖7(a)所示。應變分布發生變化，最大von Mises應變值出現在前翼槽附近，比貯存階段增大了10倍，危險點記為點A，如圖7(b)所示。

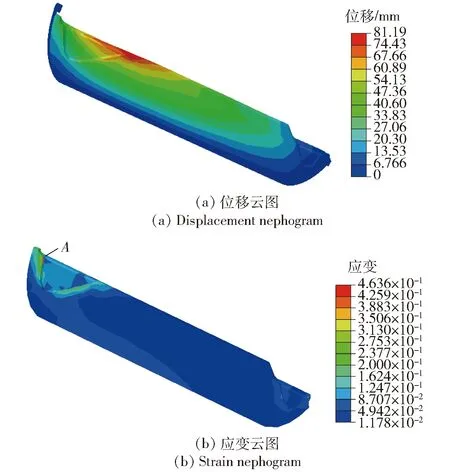
圖7 點火增壓和軸向過載仿真云圖Fig.7 Simulation nephograms under inner pressure and axial acceleration loadings

2.3.3 振動載荷

在進行固化降溫和實測振動載荷聯合作用下的數值仿真時，對ax方向施加重力載荷。圖8給出31.4 s(某一應力幅值)時藥柱外部和內部的應力分布結果，藥柱前翼及中孔處存在較明顯的應力集中。

圖8 振動載荷仿真云圖Fig.8 Simulation nephograms under vibration load

發動機藥柱在該時間點最大von Mises應力σvM值為0.066 08 MPa，遠小于推進劑的最大抗拉強度值，因此在周期性振動載荷下藥柱不會發生瞬時失效，但是周期性運動產生的累積疲勞損傷不可忽視。雖然結果表明藥柱中孔應力值較大，但計算發現其最大應力幅值為0.5 kPa，遠小于藥柱點火載荷對應的危險點A的應力幅值，因此以點A對應的應力變化趨勢作為藥柱累積損傷的計算依據，該點最大應力幅值在1.2 kPa左右，應力變化具有明顯的周期性，如圖9所示。

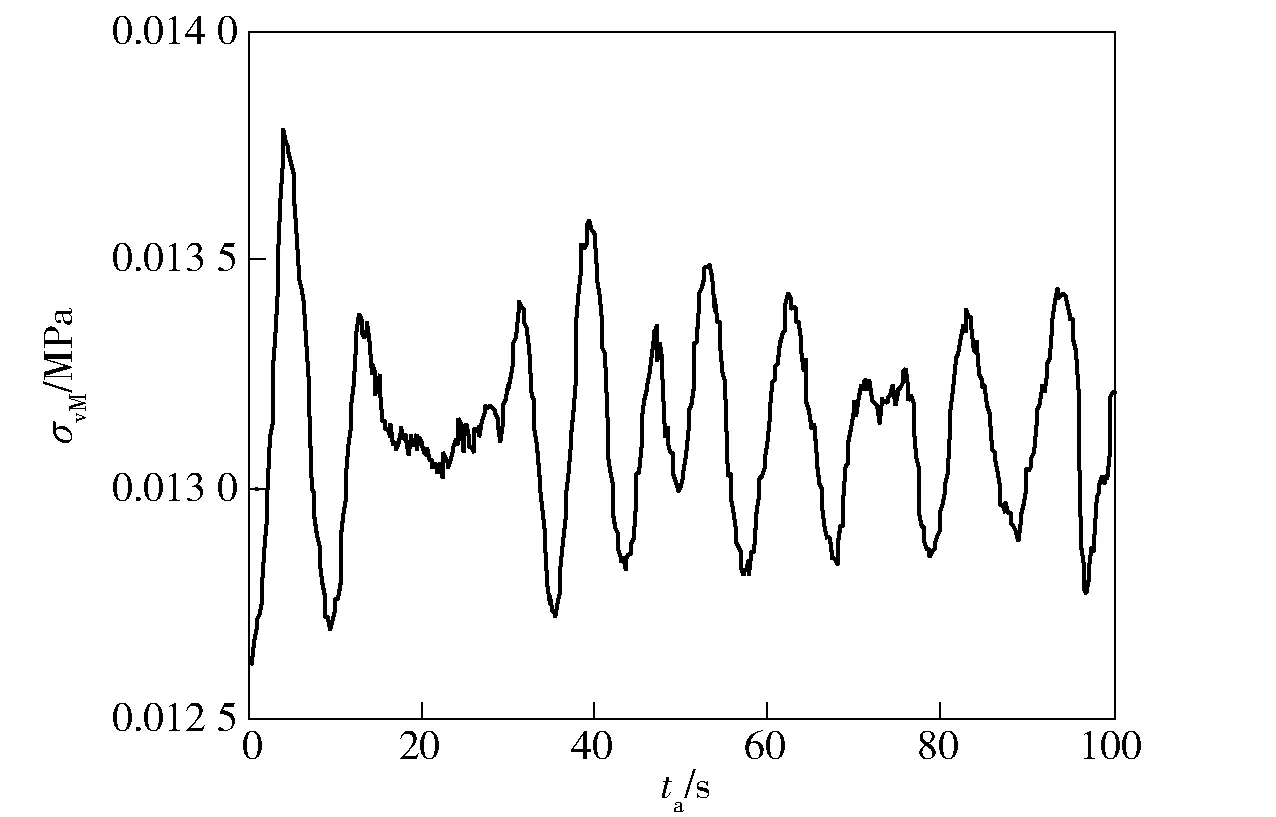
圖9 藥柱危險點應力變化規律Fig.9 Variation of stress of grain dangerous point

3 發動機藥柱貯存壽命評估

3.1 基于化學老化和立式貯存的發動機壽命評估

在前期對各工況進行數值模擬的基礎上，對工況2中立式貯存時間進行調整，以半年作為一次立式貯存周期，仿真過程中考慮不同貯存溫度和不同貯存老化時間的發動機藥柱模量變化，考慮立式貯存過程中的老化因素，忽略其他參數的影響，得到發動機經歷不同立式貯存次數下進行點火發射的仿真結果。經仿真發現，發動機經不同老化時間和靜態立式貯存時間后進行點火發射時，藥柱危險點位置并未發生變化。根據(5)式的推導方法，得出常溫下危險點von Mises應變εvM隨時間的變化規律。以工況2為例，點火之前經歷了半年時間的靜態立式貯存，考慮20%的富裕量[9]，應變表達式為

εvM=0.548 8-exp (6.921 8-2 841.2/Ts)×t.

(8)

最大von Mises應變εvM與老化試驗所得到的延伸率δm共同繪制于圖10中，在交點O處有εvM=δm成立，交點橫坐標th表示藥柱在立式貯存之前自然貯存老化的時間，即臥式貯存時間。若εvM<δm，則表明貯存多年后，發動機經歷固化降溫、靜態立貯后點火發射時產生的最大應變值小于推進劑貯存后的最大延伸率；若εvM>δm，則結果反之。因此，認為發動機臥式貯存th后歷經工況2的載荷后滿足結構完整性要求。將發動機立式貯存時間定義為tv，認為th與tv之和為發動機總的貯存壽命ttot.

圖10 應變和延伸率隨時間變化規律Fig.10 Variation of strain and extensibility with time

在該工況下，th為132.2個月，即11.02年，因此ttot=11.52年。該參數同時也表明，若發動機臥式貯存時間超過11.02年，則其無法完成1次靜態立式貯存。

3.2 考慮振動載荷的發動機壽命評估

通過雨流計數法對應力變化歷程進行計數，進而利用Miner線性損傷理論和前期擬合的推進劑疲勞本構方程計算藥柱危險點的疲勞損傷[17]。疲勞本構方程見(9)式：

lgn=8.073 3-7.800 3σ，

(9)

式中：n為推進劑的疲勞破壞次數；σ為往復拉伸試驗的應力幅值。

圖11表示100 s內應力雨流計數結果，其中C-D和C-U分別表示具有下降趨勢和上升趨勢的全循環，HC-D和HC-U分別表示具有下降趨勢和上升趨勢的半循環，圖11中共計10個全循環和5個半循環。計算得到藥柱動態立式貯存半年的累計損傷為0.017 12，損傷隨著貯存時間線性增加。

圖11 雨流計數結果Fig.11 Result of rainflow counting

以前述工況為例，考慮振動載荷下的藥柱疲勞損傷計算結果，th進一步減小，降低至129.9個月，即10.83年，發動機壽命為ttot=11.33年。表明若發動機臥式貯存時間超過10.83年，則其無法完成1次動態立式貯存。

3.3 臥式貯存時間與立式貯存次數的關系

為了探究立式貯存時間與發動機臥式貯存時間的關系，開展不同長時立式貯存期的發動機數值仿真。由于裝藥在立式貯存過程中也受老化影響，延伸率隨著貯存時間呈線性減小的趨勢。在0～20次內選擇6種貯存工況分別進行計算，由于計算結果較為密集，僅列出立式貯存0次和10次時的計算結果如圖12所示，A、B兩點分別對應兩種工況下th值。

圖12 不同立式貯存期下應變變化規律Fig.12 Variation of strain in different vertical storage times

令N表示動態立式貯存次數，圖13表示th值與N之間的關系。由圖13可見：隨著立式貯存時間tv的增加，發動機臥式貯存時間th呈減小趨勢，且變化率逐漸衰減；反之，隨著發動機臥式貯存時間th的延長，發動機后期可允許的立式貯存次數N將逐漸減小。

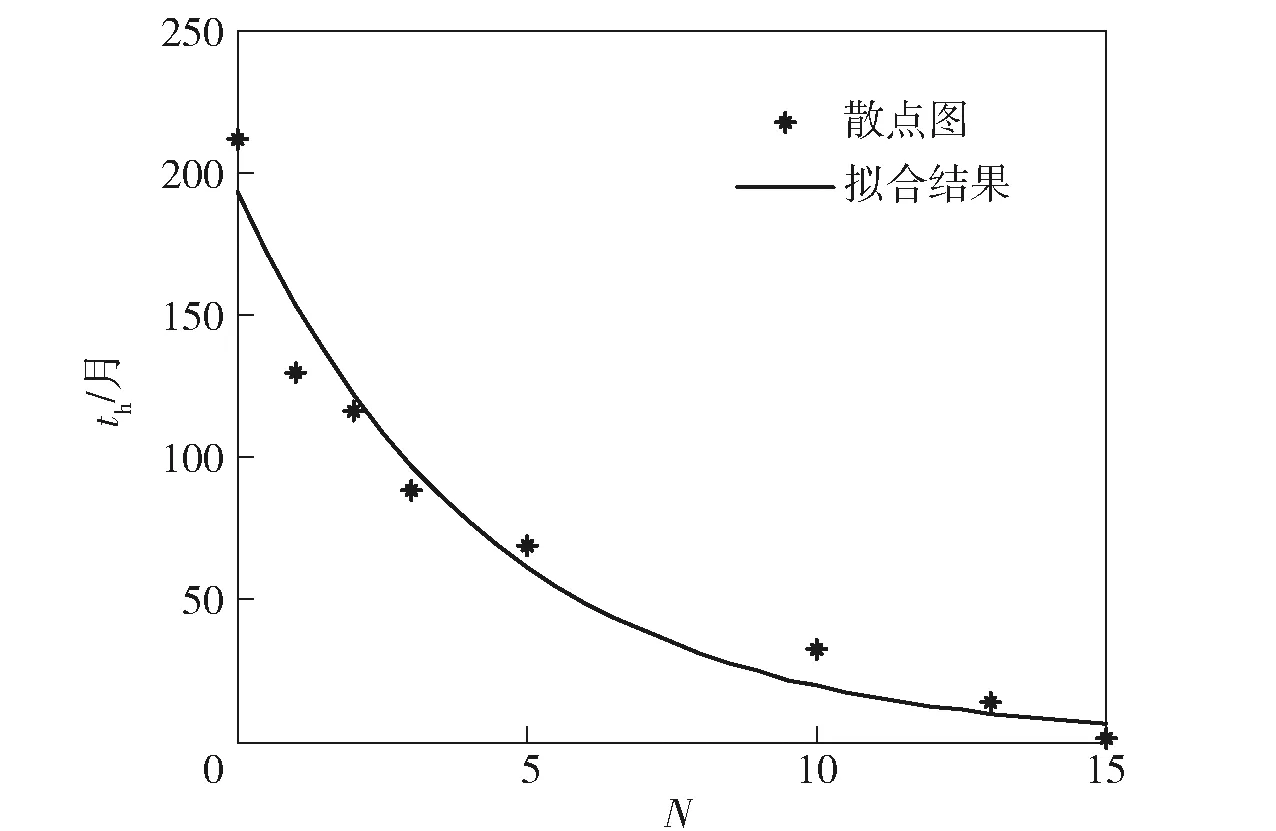
圖13 N與th之間的關系Fig.13 N vs. th

臥式貯存時間與立式貯存次數之間的關系進行擬合，將考慮到發動機從出廠至交付存在一定的時間間隔，因此th=0的情況并不存在，考慮可以用(10)式的形式來描述二者之間的關系，相關系數為96.37%，將擬合結果也繪制于圖13中。

th,min=193.3e-0.24×N.

(10)

在這里，取th,min=5月，故Nmax=15次。

ttot受th,min和N的影響，圖14表示發動機總貯存壽命ttot隨N的變化規律，隨著N的增加，發動機受老化因素和立式蠕變影響，總壽命呈減小趨勢，且變化逐漸緩慢，采用(11)式表述二者之間的關系。

ttot=9.576e-0.781 6N+8.237.

(11)

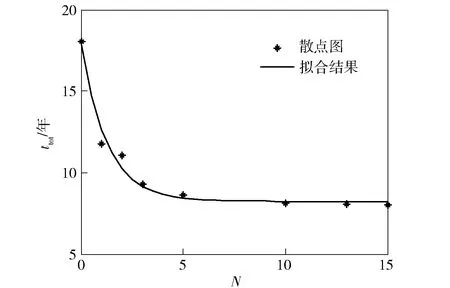
圖14 ttot隨N變化關系Fig.14 ttot vs. N

最后得出發動機總貯存壽命變化規律，考慮立式貯存時，發動機總貯存壽命介于8.24～11.75年；不考慮立式貯存時，發動機總壽命為17.81年。從結果看，立式貯存下總壽命比臥式貯存減小34.0%～53.7%，因此應對發動機立式貯存狀態引起高度重視，并應根據實際貯存情況規劃立式貯存方案。

4 結論

本文基于加速老化試驗和實測振動載荷對發動機進行了三維建模與數值仿真，預估了發動機壽命，并得出了臥式貯存時間與動態立式貯存次數之間的關系。得出主要結論如下：

1) 通過推進劑50 ℃、60 ℃和70 ℃ 3個溫度下的加速老化試驗，得出了推進劑在常溫下延伸率與貯存時間的關系式δm=60.4-exp (29.633 3-9 361/Ts)×t.

2) 有限元分析表明：在固化降溫和重力作用下，發動機前后人工脫粘層張開，藥柱整體向尾部下沉；受蠕變影響，隨著貯存時間的增加，藥柱變形量緩慢增大。之后進行點火發射，藥柱最大von Mises應變值急劇增加，發生在藥柱前翼槽。

3) 在固化降溫和實測振動載荷的聯合作用下，藥柱內部各點產生周期性的應力。藥柱危險點最大應力幅值在1.2 kPa左右，大于中孔及尾部應力幅值，藥柱動態立式貯存半年時間的累積損傷為0.017 12.

4) 對不同立式貯存時間下的發動機進行點火發射，將最大von Mises應變與延伸率進行比較，進而加之疲勞損傷，得出貯存壽命隨動態立式貯存次數的變化規律。隨著發動機貯存時間的增加，其允許立式貯存次數相應減少。

5) 推導動態立式貯存次數與臥式貯存時間之間的關系式為th=193.3e-0.24×N，同時給出最大立式貯存次數為15次，發動機總貯存壽命隨著立式貯存次數逐漸減小，介于8.24～17.81年之間。

6) 粘接界面發生破壞也是固體發動機的主要失效模式，后續應對粘接界面在聯合工況下的損傷及結構破壞展開深入研究。