基于核電廠鋁型材檢測的電磁超聲工作效率分析

李 靜

（海南核電有限公司，海南昌江 572700）

0 引言

鋁合金板材是核電廠使用的金屬材料之一[1]。電磁超聲傳感器（Electromagnetic Acoustic Transducer，EMAT）是一種非接觸型超聲發射接收裝置。電磁超聲技術檢測時無需耦合劑，無需對受檢件表面預處理，且能夠方便地產生表面波、板波、斜入射體波、垂直入射體波等多種類型的超聲波[2]，目前已成為超聲無損檢測重要技術之一[3]。利用該技術不僅可以精確地檢測板材表面缺陷，而且由于省去了耦合劑和復雜的預處理過程，可對生產過程中的高溫板材直接進行檢測，檢測效率顯著提高。

電磁超聲的缺點是效率低，為了研究影響EMAT 效率的參數，建立EMAT 模型，研究表面波EMAT 的線圈、磁鐵參數與EMAT 效率間的關系。本文將簡要介紹電磁超聲工作機理；通過建立EMAT 三維有限元模型獲得表面波EMAT 各參數與其效率間的關系；最后通過實驗驗證結論的有效性

1 EMAT 換能機理及其數學模型

EMAT 由磁鐵、線圈和鋁型材三部分組成。傳感器發射超聲波的原理如圖1 所示。發射過程中，線圈中通過發射電流。根據電磁感應定律，該電流會在鋁板內感生出渦流。渦流在磁鐵靜磁場的作用下產生洛侖茲力，洛侖茲力引發鋁板表面質點的高頻振動，從而產生超聲波。表面波的接收是其發射的逆過程。

三維實體模型由線圈、磁鐵、鋁板和空氣4 部分組成。其中，空氣單元用于模擬EMAT 工作環境中的遠場空間。由于該模型關于YOZ 平面對稱，為了減少運算量，研究中僅建立了半個EMAT 模型。隱去空氣單元后的EMAT 實體模型如圖2 所示，進一步隱去磁鐵后的實體模型如圖3 所示。所建實體模型中，EMAT 線圈的匝數為4 匝，匝間距為3 mm；釹鐵硼永磁鐵的剩磁為1.2 T；脈沖發射電流幅值為50 A，頻率為500 kHz。三維有限元模型如圖4 所示。采用共軛梯度法求解該模型，可獲得EMAT 工作過程中產生的渦流、磁場以及Lorentz 力的數值及其分布規律。

2 EMAT 效率的特性分析與研究

本節將通過求解EMAT 有限元模型獲得不同參數下換能器產生的洛倫茲力，并根據公式進一步得到所激發的表面波能量密度，最終完成EMAT 效率的特性分析與研究。

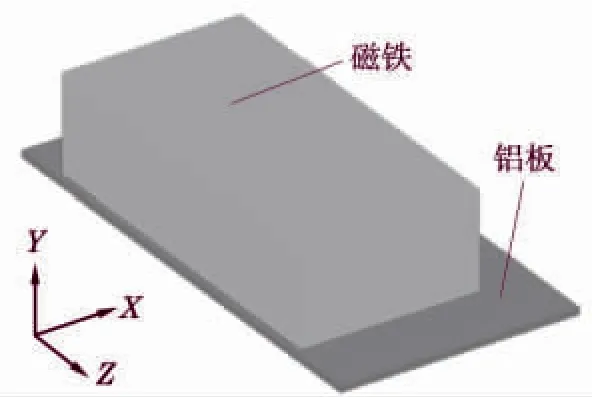
圖2 鋁板和磁鐵三維模型

以提離距離0.1 mm，導線長度30 mm，導線寬度0.5 mm，磁鐵長度60 mm，磁鐵寬度60 mm，磁鐵高度20 mm 的仿真模型為例求得的渦流分布如圖5 所示，鋁板表面的渦流主要分布于線圈正下方。磁感應強度分布如圖6 所示，磁感應強度在磁鐵中心處較弱而在邊沿處較強。鋁板表面洛倫茲力的分布如圖7 所示，鋁板表面洛倫茲力與渦流的分布規律近似，并且在磁鐵中心下方較小，在磁鐵邊沿下方較大。

為了便于分析，本文將選取鋁板中的某些典型位置進行研究。典型位置A 和B 如圖8所示。在所建模型基礎上，本文將著重分析和研究電磁超聲能量密度隨EMAT 提離距離G、線圈長度CL、線圈寬度CW、磁鐵長度ML、磁鐵寬度MW以及磁鐵高度MH等參數（圖9）變動時的變化規律，為工程應用中EMAT 效率的優化設計奠定基礎。

根據EMAT 在鋁板檢測中的實際情況，確定各參數的取值范圍，G：（0.1～1.3）mm，CL：（25～49）mm，CW：（0.1～1.7）mm，ML：（30～62）mm，MW：（46～62）mm，MH：（10～26）mm。為了使仿真模型與實驗參數一致，仿真模型中G 為0.1 mm，CL為30 mm，CW為0.5 mm，ML為 60 mm，MW為60 mm，MH為20 mm。在研究不同參數的變化規律時，保持其他5 個參數與上述參數相同。

（1）EMAT 效率與線圈長度的關系。選取（25～49）mm，步進為3 mm 的9 組線圈長度分析其對效率的影響。通過這9組數據進行最小二乘擬合得到線圈長度與效率的關系曲線（圖10）。

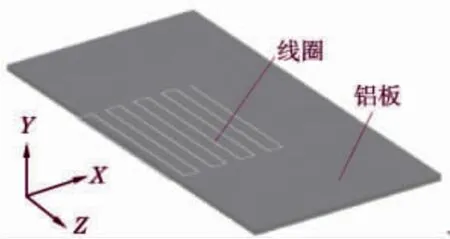
圖3 線圈與鋁板的三維模型

圖4 EMAT 三維有限元模型

圖5 渦流分布

圖6 磁感應強度分布

圖7 洛倫茲力分布

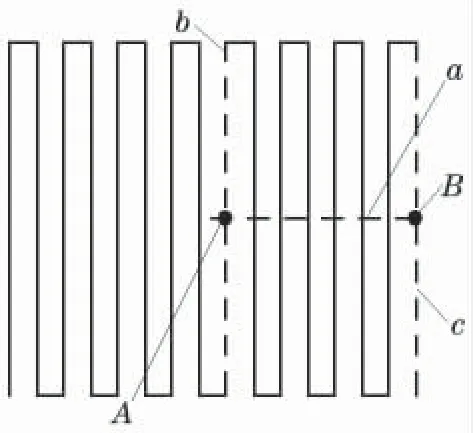
圖8 典型位置A 和B

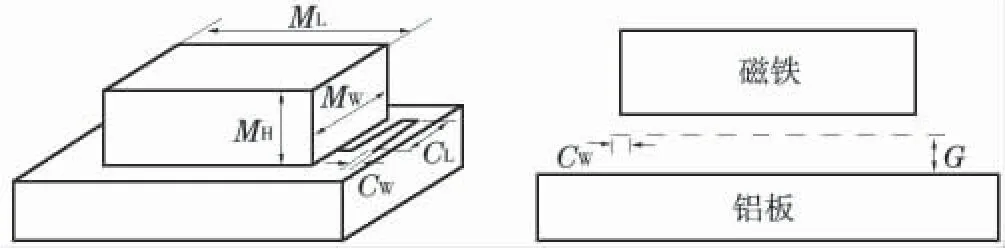
圖9 EMAT 的關鍵參數示意

EMAT 效率與洛倫茲力有關。由于G 不變使磁鐵的磁場強度和電流在鋁板表面A、B 兩點處產生的渦流保持不變，因此對洛倫茲力影響較小。改變線圈長度對提高EMAT 效率作用不大。

（2）EMAT 效率與線圈寬度的關系。選取（0.1～1.7）mm，步進為0.2 mm 的9 組線圈寬度分析其對效率的影響。通過這9 組進行最小二乘擬合得到線圈寬度與效率的關系曲線（圖11）。

曲折線圈相鄰兩根導線中交變電流產生的合磁感應強度在導線正下方最強，兩根導線中間處最弱。當線圈變寬時，相鄰導線交變電流產生的磁感應強度重疊范圍增加，磁感應強度削弱作用加強，渦流減小導致洛倫茲力降低。因此為提高效率應減小線圈寬度。

（3）EMAT 效率與磁鐵長度的關系。選取（30～62）mm，步進為4 mm 的9 組磁鐵長度分析其對效率的影響。通過這9 組數據進行最小二乘擬合得到磁鐵長度與效率的關系曲線（圖12）。

磁鐵的磁力線在邊沿處較短，磁阻較小，因此邊沿處磁感應強度較大。當磁鐵長度增加時，中心處的磁感線長度增加磁阻變大，磁感應強度減小導致渦流受到的洛侖茲力變小，效率降低。

（4）EMAT 效率與磁鐵寬度的關系。選取（46～62）mm，步進為2 mm 的9組磁鐵寬度分析其對效率的影響。通過這9 組數據進行最小二乘擬合得到磁鐵寬度與效率的關系曲線（圖13）。

磁鐵的磁力線在邊沿處較短，磁阻較小，因此邊沿處磁感應強度較大。當磁鐵寬度增加時，中心處的磁感線長度增加磁阻變大，磁感應強度減小導致渦流受到的洛侖茲力變小，效率降低。

圖10 線圈長度與效率曲線

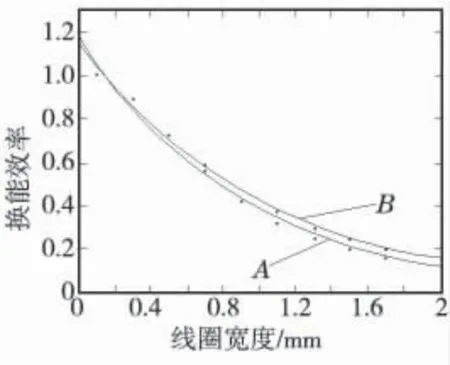
圖11 線圈寬度與效率曲線

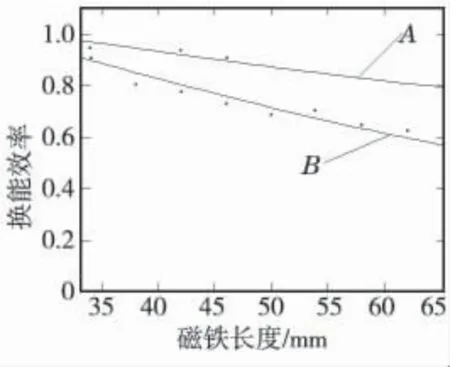
圖12 磁鐵長度與效率曲線

（5）EMAT 效率與磁鐵高度的關系。選取（10～26）mm，步進為2 mm 的9 組磁鐵高度分析其對效率的影響。通過這9 組數據進行最小二乘擬合得到磁鐵高度與效率的關系曲線（圖14）。

磁鐵高度增加時，磁感應強度增加，渦流受到的洛侖茲力增加，效率增加。

綜合對磁鐵的長寬高的實驗，為提高效率，在使用磁鐵時應在覆蓋線圈和保證磁感應強度相同的前提下，盡量選擇橫截面積較小，高度較高的磁鐵。

（6）EMAT 效率與提離距離的關系。選取（0.1～1.3）mm，公差0.15 mm 的9 組提離距離分析其對效率的影響。通過這9 組數據進行最小二乘擬合得到提離距離與效率的關系曲線（圖15）。

當提離距離增大時，交變電流產生的磁感應強度減小，鋁板表面感生出的渦流減小，渦流受到的洛侖茲力減小。因此，為提高效率應減小提離距離。

通過仿真實驗，能夠清楚地看出效率與各參數之間地關系。為提高效率，線圈應盡量減小提離距離和線圈寬度；磁鐵在保證磁感應強度前提下，應盡量減小橫截面積，增加高度。

3 實驗驗證

本文通過有限元仿真已經得出效率與各參數關系。下面將通過實驗驗證。實驗參數如下：線圈長30 mm，線圈寬0.5 mm，磁鐵長60 mm，磁鐵寬60 mm，磁鐵高20 mm，線圈匝數為8匝，匝間距3 mm，鋁板長度為500 mm，鋁板寬度為150 mm，鋁板厚度為30 mm，發射線頻率500 kHz，電流幅值為156 A。圖16 為實驗設備照片，示波器上的波形為接收換能器接收到的回波波形。

本文實驗只驗證傳感器與鋁板間距離與效率關系的有效性。首先改變發射換能器與鋁板之間的距離，然后測試接收到的回波幅值，判斷二者之間的關系是否與仿真結果吻合。表1 為實驗結果，其中，A 表示回波幅值。

仿真獲得的結果與實驗獲得的結果變化趨勢一致，但存在一定的差異其可能的原因是本文的仿真分析忽略了Z 方向的洛倫茲力，而實際中由于線圈端部電流受到的洛倫茲力沿Z 方向分布，因此導致二者存在差異；另外，本文假定縱波波速3140 m/s，橫波波速6380 m/s，而不同的鋁板在不同的溫度下其波速不同，這也會造成實驗與仿真結果不同。

圖13 磁鐵寬度與效率曲線

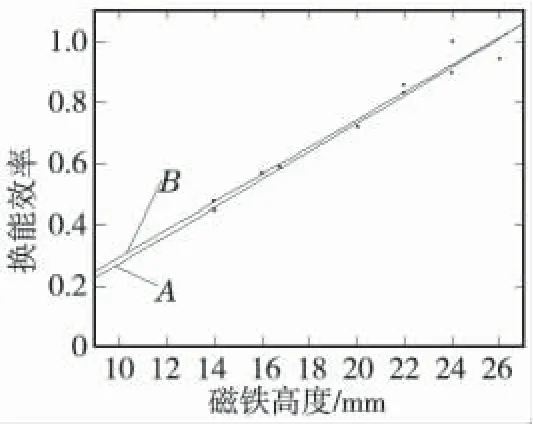
圖14 磁鐵高度與效率曲線

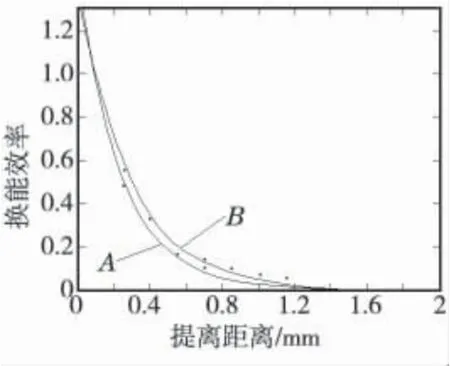
圖15 提離距離與效率曲線

圖16 實驗設備

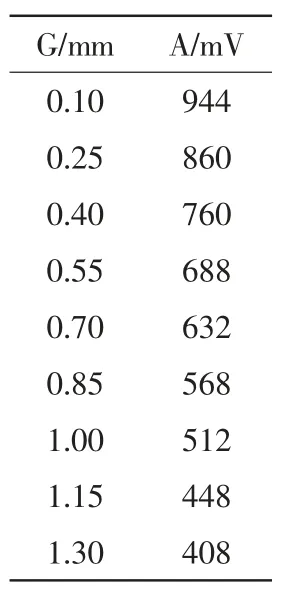
表1 提離距離實驗結果

4 結論

通過建立三維有限元模型，對用于鋁板檢測的EMAT 效率進行了分析，并通過MATLAB 曲線擬和方法獲得EMAT 關鍵參數與效率的關系曲線。以提高效率為目的研究了線圈和磁鐵參數對效率的影響。所得結論如下。

（1）線圈與鋁板表面的距離增大時，線圈內的交變磁場在鋁板表面產生的渦流減小，磁鐵在渦流處產生的磁感應強度減小，導致效率下降，因此為提高效率應減小提離距離。

（2）曲折線圈的長度增加時，磁鐵在線圈中心處的磁場和鋁板表面的渦流幾乎無變化，因此線圈長度對效率影響較小。

（3）線圈寬度增加會顯著減小鋁板表面的渦流，此時相鄰導線產生的交變磁場重疊部分增加，削弱作用增強。因此為提高效率應減小線圈寬度。

（4）磁鐵長度或寬度增加時磁鐵表面中心處磁感應強度降低。這會導致線圈中心處的效率下降。在完全覆蓋線圈和保證磁感應強度的前提下，為提高效率應盡量減小磁鐵長度或寬度。

（5）磁鐵高度增加時，磁感應強度增加，效率增加。所以增加磁鐵高度能有效提高效率。