基于譜峭度的同步提取變換方法及故障診斷應用

張 浩，張 坤，田偉康，胥永剛

（北京工業大學先進制造技術北京市重點實驗室，北京 100124）

0 引言

旋轉機械廣泛地應用于機電設備中，而在多數旋轉機械中滾動軸承起到至關重要的作用，被人們稱為機器的關節[1]。伴隨著我國科技水平的提升，在實際工況中常伴隨著高溫差、高壓力差、強噪聲等惡劣環境，在這種工況下滾動軸承很容易造成損傷并且很難保持平穩的工作狀態，極易發生輕微損傷并且較難精準確定損傷部位[2]。因此采集軸承的振動信號監測其狀態并診斷故障具有非常重要的工程應用價值[3]。同步提取變換（Synchroextracting transform，SET）通過提取短時傅里葉變換（Short-time Fourier transform，STFT）在瞬時頻率位置的時頻系數可獲得較理想的時頻譜。該方法一方面提高了時頻分辨率，另一方面亦減少了交叉項的影響，一定程度上抑制了噪聲對STFT 時頻譜的干擾，然而在SET 時頻譜的基礎上進行自適應故障診斷拓展應用方面尚待進一步研究。

在時頻分析方法中，短時傅里葉變換、Wigner-Ville[4]時頻分布、小波分析、離散小波變換、雙樹復小波變換以及近年來提出的基于自適應分解理念的同步壓縮變換（Synchrosqueezing transform，SST）等方法[5-6]。S.Vulli 針對發動機的振動研究中，利用STFT 得到信號的二維時頻譜，并成功識別出了發動機正常工況下的爆燃激勵及各種故障特征[7]。Yang Jin 比較了STFT 與其他時頻分析方法的特點與優劣，并利用發動機振動信號驗證了各種時頻方法適用范圍。J Antoni 發現信號中的非平穩分量，在時頻譜中本身的特征頻率附近具有較大的峭度值，通過計算STFT 譜中各頻點的峭度特征，有效提取到信號中的非平穩分量[8-9]。

基于時頻變換分辨率不高的問題，于剛[10]在STFT 的基礎上提出一種新的時頻分析方法SET。該方法在STFT 的基礎上用兩個窗函數對信號進行傅里葉變換，然后對得到的兩個新的一維信號對比分析，通過閾值對數據進行篩檢，最后得到一組新的數據，也就是同步提取變換后的信號。同步提取變換具有時頻分辨率高，可用于模態分解、弱信號檢測、S 變換等方法和實時計算。但該文獻中并未繼續深入研究信號的自適應提取問題。自適應獲取信號分量有利于進一步診斷故障，將SET 理論向實用方向拓展。

提出了一種基于譜峭度的自適應信號處理方法，利用峭度值對周期性沖擊信號的敏感性，將譜峭度與SET 相結合，可以快速、準確地判斷故障特征頻率的位置及自適應的提取特征頻率，再對提取的分量進行包絡分析，成功提取了滾動軸承的故障特征信息。

1 同步提取變換基本原理

同步提取變換（SET）[7]提取瞬時頻率的時頻系數，所攜帶的噪聲大大減少，魯棒性得到增強。其步驟分為以下3 步：①根據STFT 計算時頻譜；②根據相位信息估計瞬時頻率；③提取STFT在瞬時頻率位置的時頻系數。

該方法首先需要根據STFT 計算信號s（t）的時頻譜：

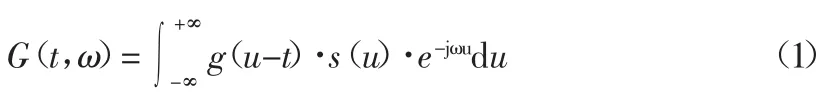
對式（1）乘以相位因子ejωt：

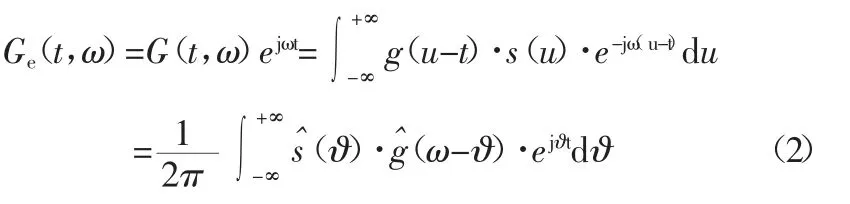
式（2）表示該方法在保證窗函數不變的前提下移動信號進行FFT 計算。根據文獻［10］此處選取的窗函數為高斯窗，窗函數越短，時間分辨率越高，窗函數越長，頻率分辨率越高。為了保證時頻圖的時頻聚集性，窗寬的選擇應該適中。具體的窗寬選擇應根據數據的長度進行確定。中設頻率為ω0的諧波信號s（t）=A·ejω0t，其頻域表示為：

將式（3）代入式（2），則時頻譜可表示為：

式（4）說明，一系列與諧波信號頻率一致的時頻系數組成諧波信號的STFT 譜。由于窗函數在頻域緊支且在0 頻率處有最大值，因此在時頻譜中頻率ω=ω0處的時頻系數幅值最大，為。此時距離ω0越遠的時頻系數幅值越小。可采用式（5）估計STFT 譜中時頻系數的瞬時頻率。

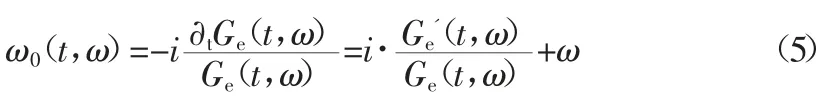
其中，?tGe（t，ω）是Ge（t，ω）對時間的一階偏導數。由此在二維時頻平面中，可以得到一個與STFT 譜系數一一對應的新的時頻譜ω0（t，ω）。

僅提取STFT 譜在瞬時頻率位置的時頻系數，對應公式可表示為：

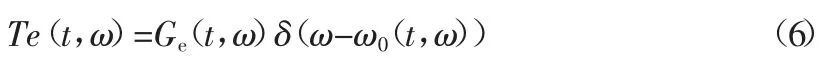
其中，δ（ω-ω0（t，ω））稱為同步提取算子。

同步抽取變換的逆變換如式（7）所示：

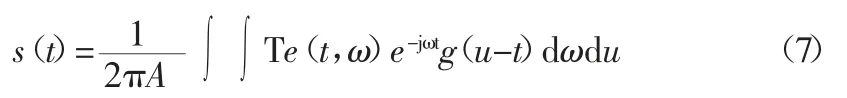
文獻［10］將信號的重構問題近似為STFT 譜的脊提取問題，但其重構方法為簡單的數據疊加處理。本文進一步研究了信號分量的分解與重構，利用順序統計濾波器對信號的邊際譜進行頻帶劃分，將時頻譜中不同的信號分量分割開來分別重構，并拓展應用于滾動軸承故障診斷中。

同步提取變換重構如式（8）所示：

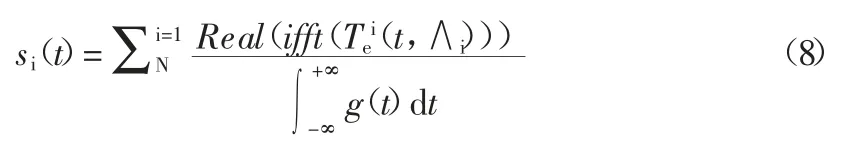
2 改進快速譜峭度

同步提取變換信號重構步驟：

快速譜峭度圖需要構建濾波器進行濾波處理，但是同步提取變換本身帶有濾波效果，不需要再次進行濾波處理。基于同步提取變換的改進快速譜峭度圖算法的流程如下：

（1）對信號進行同步提取變換。

（2）在時頻圖上對SET 處理后的信號進行連續層數劃分。

（3）對劃分好的數據進行重構。

（4）對重構后的信號求取峭度值，得到改進后的峭度圖（圖1）。

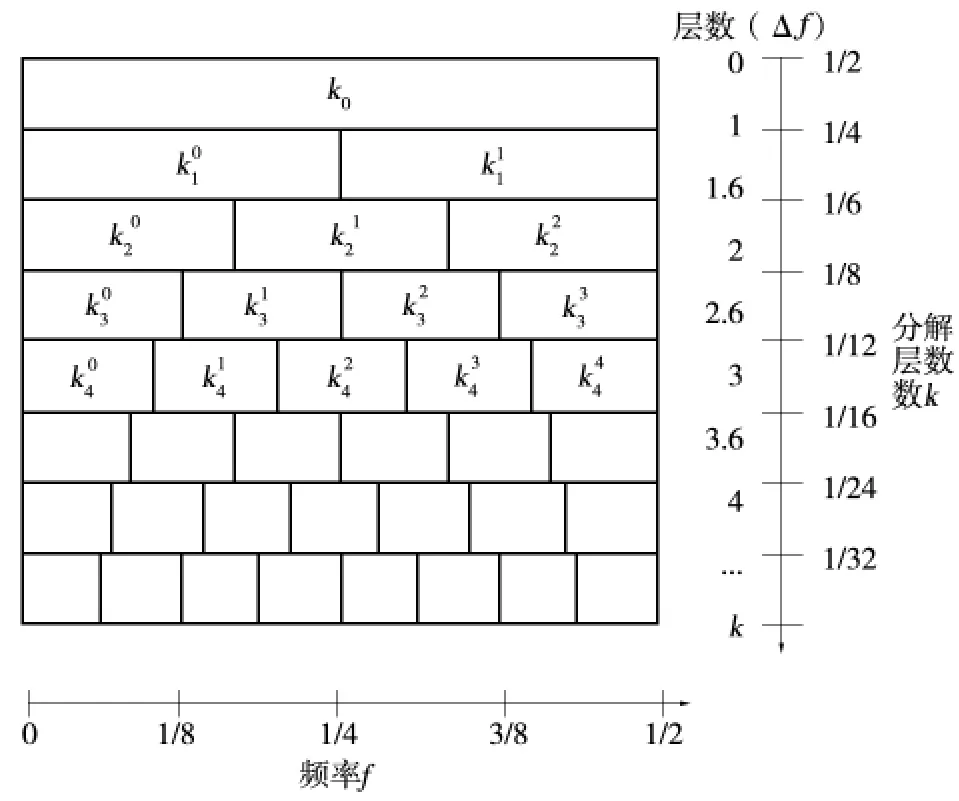
圖1 改進快速譜峭度

3 仿真信號分析

為了驗證修改方法的可行，構建一個仿真信號x（t）如式（9）所示。

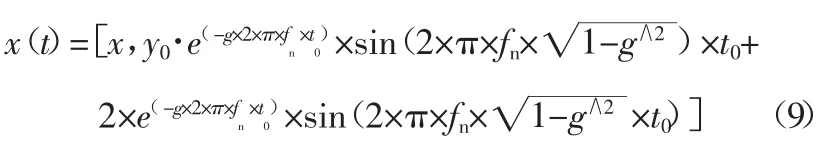
其中，fn為固有頻率，t0為單周期采樣時刻，g 為阻尼系數，y0為位移常數。

對該仿真信號添加噪聲，信噪比為-1 dB。疊加后的信號的時域波形如圖2 所示，

圖2 加噪信號波形

通過同步提取變換對信號s（t）進行處理，然后求得峭度值，最后得到峭度圖（圖3）。

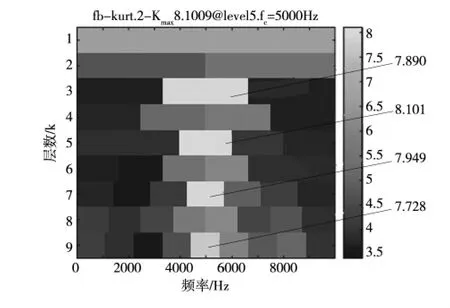
圖3 SET 改進峭度

從峭度圖中得到，峭度值最大位于第五層第三部分。這部分峭度值最大說明該頻段內的信號沖擊最為明顯，因此對該部分進行提取并作進一步分析。

在這里確定了峭度圖上最大峭度的位置，然后利用改進同步提取變換方法，對峭度最大處進行信號提取（圖4）。

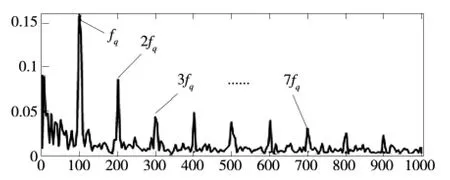
圖4 包絡分析

從圖4 中可以找到特征頻率及其倍頻，驗證了本方法的正確性。

4 實驗信號分析

取型號6307 滾動軸承并預置外圈故障，測取其振動信號。電機轉速為1496 r/min，采樣頻率7100 Hz。計算求得該軸承內圈轉頻為24.93 Hz，外圈故障特征頻率為77.3 Hz，信號的波形如圖5 所示。

圖5 原始信號波形

對信號進行同步提取變換處理，求峭度值，最后得到峭度圖（圖6）。

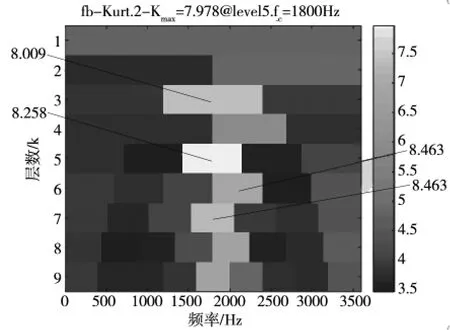
圖6 改進峭度

從峭度圖中得到，最大的峭度值位于第五層第三部分。表明該部分的周期性信息最為明顯，因此可以對其進行故障信息的提取分析。

通過對峭度圖上最大峭度位置的識別，利用改進同步提取變換方法，對峭度最大處進行信號提取（圖7）。

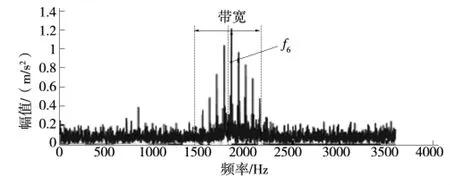
圖7 信號提取示意

對提取的信號進行包絡分析，得到包絡圖（圖8）。

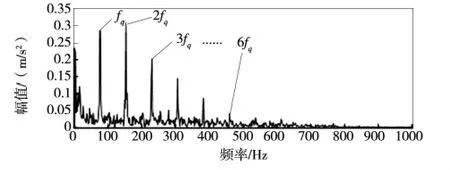
圖8 包絡分析

從圖8 中可以找到該軸承外圈故障特征頻率及其倍頻，由此可以判斷該軸承外圈出現故障。驗證了本方法的正確性。

5 結語

（1）提出了一種基于譜峭度的同步提取變換方法，實現了信號的自適應分解，可提取滾動軸承振動信號中的周期性沖擊分量。

（2）仿真信號和實驗信號驗證了該方法的可行性。

（3）將基于譜峭度的同步提取變換方法應用于滾動軸承故障診斷，可以有效地提取故障信息。