高水頭水工隧洞鋼筋混凝土襯砌承載特性分析
朱奎旭,肖 明,陳俊濤,王安亭
(1. 武漢大學 水資源與水電工程科學國家重點實驗室,武漢 430072;2. 武漢大學 水工巖石力學教育部重點實驗室,武漢 430072)
0 引 言
圓形有壓水工隧洞運行時鋼筋混凝土襯砌受內水壓力的作用,其環向應力一般表現為拉應力,在高水頭的作用下,混凝土容易超出其抗拉強度產生裂縫進而導致內水外滲。目前,針對高水頭的水工隧洞一般采用透水襯砌的設計原則,認為承擔較大內水壓力的鋼筋混凝土襯砌必然會開裂,內部的高壓水通過裂縫進入圍巖,使得隧洞外的滲透壓增大,進而對隧洞自身和圍巖的穩定產生影響[1-3]。因此合理模擬水工隧洞襯砌承載過程中的損傷開裂行為,對地下鋼筋混凝土襯砌管道設計和水工隧洞區域圍巖穩定校核具有重要意義。
針對透水襯砌的設計原則,我國《水工混凝土結構設計規范》(SL 191-2008)和《水工隧洞設計規范》(SL 279-2016)基于大量的實驗數據給出了裂縫寬度計算的近似公式,但公式具有較強的工程依賴性。潘家錚[4]提出了以圍巖和內水壓力為主要影響因素的裂縫計算方式,但該公式未考慮鋼筋對裂縫的限制作用;劉秀珍[5]基于有限元的思想,將鋼筋混凝土襯砌看成是彈性地基上的曲梁結構,但其假定圍巖不發生開裂,切向抗力沿接觸面均勻分布。針對透水襯砌的數值模擬,肖明等[6]基于彈塑性損傷有限元,提出了襯砌裂縫寬度的估算公式;蘇凱等[7]基于滲透水壓力以體力方式施加的原則,提出了圍巖和襯砌聯合承載的耦合分析方法。高水頭水工隧洞襯砌開裂不可避免,開裂后由于混凝土與鋼筋的變形不再保持協調,兩者在接觸面上勢必會產生黏結滑移。目前有關水工隧洞襯砌黏結滑移行為的研究較少,相關實驗表明黏結滑移行為對鋼筋混凝土構件的承載能力、裂縫分布均有重要影響。因此本文基于前人的研究成果,為反應襯砌開裂階段鋼筋與混凝土黏結滑移行為的影響,在彈塑性損傷有限元計算中考慮黏結應力的作用,采用耦合計算方法研究內水壓力增大過程中水工隧洞襯砌的受力損傷特征,并對損傷開裂前后滲流場及圍巖破壞區的分布進行分析。
1 鋼筋混凝土襯砌加載狀態
由鋼筋混凝土構件加載變形的特點,可將整個變形過程分為線彈性階段、彈塑性損傷階段、損傷開裂滑移階段。相鄰階段的分界點為混凝土進入損傷演化過程、混凝土單元達到極限拉應變產生開裂。水工隧洞的實際監測數據表明,襯砌的鋼筋應力一般低于其屈服強度,因此本文不考慮鋼筋的塑性行為。
1.1 線彈性階段
內水壓力較低時,鋼筋混凝土襯砌不會開裂,此時混凝土幾乎不發生損傷,鋼筋和混凝土處于彈性狀態,應力應變呈線性關系。此時,根據有限元基本方程,由鋼筋與混凝土之間的變形協調,可得到單元的彈性矩陣:
[H]e=[Hc]+[Hs]
(1)
式中:[Hc]為混凝土彈性剛度張量;[Hs]為鋼筋彈性剛度張量。混凝土視為均勻各向同性材料,鋼筋采用桿單元模型,相應的矩陣形式見文獻[8]。
1.2 彈塑性損傷階段
當混凝土單元進入塑性狀態時,混凝土損傷開始,此時混凝土的本構關系采用考慮損傷的彈塑性材料增量形式[9]:
(2)
式中:D表示材料的損傷內變量;Hep為彈塑性矩陣[6];δij為Kronecker Delta函數。單元剛度矩陣疊加形式與式(1)相同。
對于混凝土損傷,采用Mazars的混凝土拉伸試驗擬合的演化方程來模擬[10]:
(3)
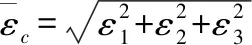
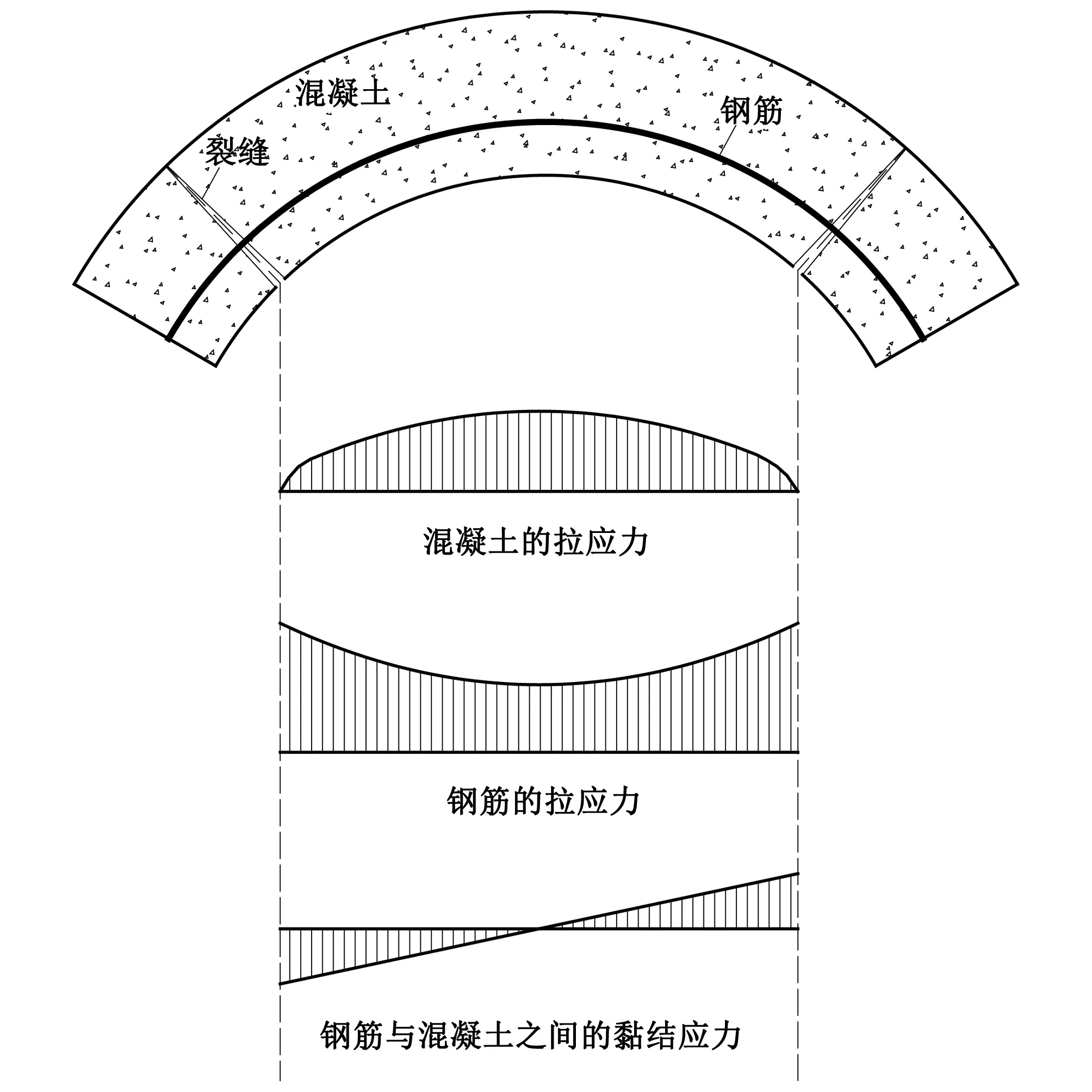
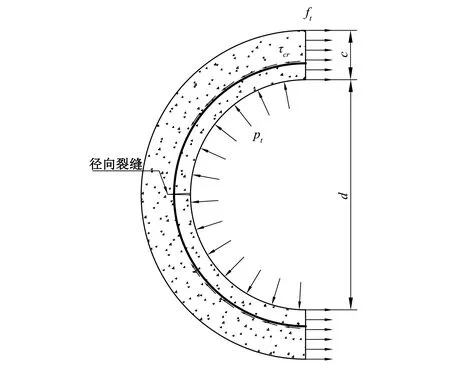
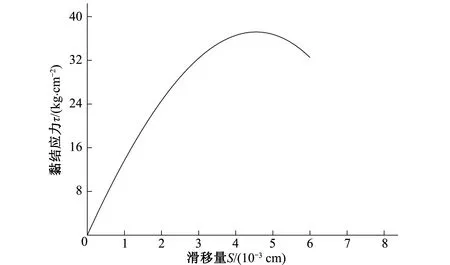
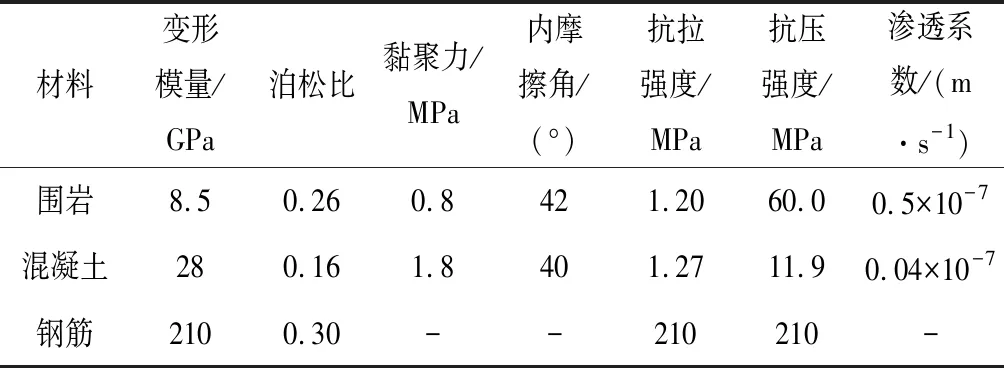
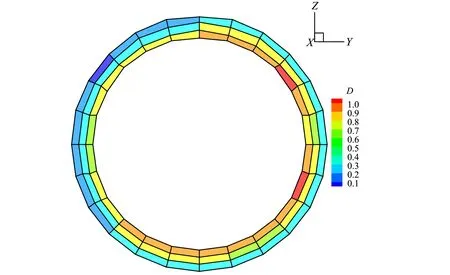
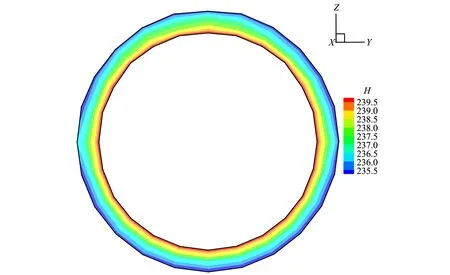
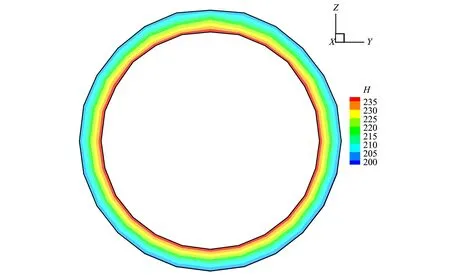
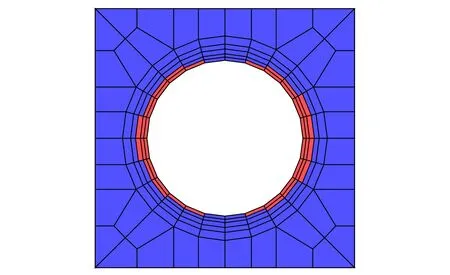
式中:At,Bt、 為試驗曲線擬合常數,對于一般混凝土0.7 一般認為當混凝土單元達到極限拉應變或者計算所得的損傷量值達到0.90后,混凝土單元產生開裂[11]。假設襯砌開裂的發展方向垂直于單元最大主應變方向,沿此方向的混凝土剛度會逐漸降低,開裂的混凝土單元剛度矩陣應按照各向異性材料進行修正[12],修正后的矩陣需轉換為整體坐標系下的應力應變矩陣: (4) 式中:βt為殘余抗剪系數,描述開裂混凝土的殘余抗剪能力;Ec、v分別為混凝土的彈性模量和泊松比。 工程監測數據表明,水工隧洞襯砌開裂后,鋼筋應力在裂縫處達到最大值,在兩個裂縫中間為最小值。鋼筋應力大小沿縱向發生變化,其表面必然有相應的黏結應力分布,如圖1所示。黏結應力的存在使得混凝土內的鋼筋平均應變小于鋼筋單獨承載時的變形,被稱為鋼筋混凝土構件的受拉剛化效應[13]。剛化效應的存在導致襯砌開裂后裂縫間的單元剛度會得到提高,使得這部分單元更易處于彈塑性損傷階段而不會產生開裂。 圖1 實驗擬合黏結應力模型Fig.1 Experimental fitting bond stress model 當水工隧洞襯砌形成徑向裂縫時,裂縫處的黏結應力達到最大值,構件達到臨界黏結狀態,此時的黏結應力稱為劈裂應力τcr,如圖2所示,可由相應的經驗公式求得[13]: (5) 式中:ft為混凝土的抗拉強度設計值;c、d為水工隧洞的形狀參數。 圖2 水工隧洞劈裂應力示意圖Fig.2 Schematic diagram of splitting stress in hydraulic tunnel Schleiss A J等[14]通過實驗數據擬合黏結應力量值在裂縫之間線性變化,在相鄰裂縫中截面處為0,如圖1所示。定義單元內鋼筋與混凝土間的黏結應力為ητcr,其中η=0~1,在相鄰裂縫中截面處取0,在含裂縫的單元處取1。 鋼筋混凝土的黏結滑移本構模型一般定義為黏結應力與滑移量之間的關系[15]: τ=14.9×103S-1.16×106S2-0.07×109S3 (6) 式中:τ為黏結應力量值;S為滑移量,即鋼筋與混凝土接觸面上的相對位移,圖3為相應的τ-S曲線。 圖3 黏結滑移曲線擬合模型Fig.3 Bond slip curve fitting model 根據襯砌單元內鋼筋與混凝土之間的黏結應力ητcr求取相應的滑移量S,由于除裂縫所在單元外,其余單元黏結應力均未達到最大黏結應力,因此計算所得滑移量S唯一。單元內鋼筋與混凝土的應變差值為Δε=S/L,L為襯砌單元內環向鋼筋的長度。襯砌單元應力可用混凝土應變Δεc表示,如式(7),有限元方程求解的未知量為襯砌單元內混凝土的位移值。 (7) [R]=(cosα·cosβsinα·cosβsinβ0 0 0)T (8) 式(7)右端第二項表示鋼筋額外伸長對應的部分應力,可用初應力法計算其等效節點荷載代入有限元控制方程中,如式(9)所示。 {Fs}e=?Ω[B]T[Hs][R]{Δε}dxdydz (9) 式中:[B]為應變計算矩陣。 襯砌的滲透損傷耦合計算采用間接耦合的方式,滲流場通過滲透體積力影響結構的應力場,進而影響材料的損傷演化;結構的損傷開裂通過改變滲透系數從而對滲流場的分布產生影響。 對于各向異性的均勻介質,根據達西定律,可以導出穩定滲流場的微分方程: (10) 式中:帶下標的k為計算坐標下的滲透系數;Q為內源;H為水頭。 對上式進行積分求和,得出三維有限元滲流方程: [A]{H}={F} (11) 式中:{H}為結點水頭列向量;{F}為滲流邊界積分得到的結點荷載;[A]為滲流有限元單元傳導矩陣。 滲流場計算完成后,滲透荷載以體積力的形式作用于應力場,形成作用在模型節點上的等效荷載[16]: (12) 式中:γ為水的重度;[N]為有限元插值形函數;H為結點水頭;Ω為單元積分域。 混凝土和圍巖的力學特性及損傷破壞機制較相近,因此基于Louis[17]鉆孔加壓實驗的滲透系數與正應力的經驗公式,考慮損傷演化對滲透系數的影響,引入滲透突跳系數ξi描述混凝土應力損傷開裂對滲流的影響。表1為不同單元狀態的滲透突跳系數ξi取值。考慮應力和損傷影響后的主應力方向滲透系數為: k=ξik0ebσi (13) 式中:k0為混凝土材料初始滲透系數;b為試驗確定的耦合系數;σi為單元有效應力。 表1 不同單元狀態下的滲透突跳系數Tab.1 Penetration mutation coefficients at different status 某電站位于我國河南省境內,設計總裝機規模1 000 MW,由上水庫、下水庫及輸水發電三大系統組成。電站上下游水庫間直線距離1.88 km,平均水頭240 m。 計算模型包括引水隧洞的上游有壓洞段、高壓岔洞段以及下游有壓洞段。本文主要針對上游有壓洞段分析,開挖洞徑為9.6 m,襯砌后過水洞徑為8.0 m,襯砌厚度為0.8 m。模型坐標系為:坐標原點位于高壓岔洞交叉中心;X軸沿洞軸線指向下游為正,范圍-124.81~58.78 m;Y軸垂直于水流方向,范圍-68.70~46.00 m;Z軸與大地坐標重合豎直向上為正,深度范圍由-29.07~380.00 m。模型共剖分475 113 個8結點等參單元,其中襯砌單元13 464 個,開挖單元6 732 個。引水隧洞區域有限元模型如圖4所示,引水隧洞鋼筋混凝土襯砌的有限元模型如圖5所示。模型中各項材料參數取值見表2。 圖4 引水隧洞區域有限元模型Fig.4 Finite element model of the diversion tunnel area 圖5 引水隧洞襯砌單元模型Fig.5 Model of the lining element of the diversion tunnel 表2 材料參數Tab.2 Parameters of materials 初始地應力場通過實測地應力反演獲得,隧洞區域第一主應力在-5~-10 MPa范圍內,屬于偏低應力場。計算程序采用課題組自主開發的三維彈塑性損傷有限元程序,并在此基礎上進行改進。對該有壓管段進行以下計算:洞室在支護條件下進行開挖;隧洞充水運行,襯砌結構在滲流場的作用下損傷開裂。為了保證非線性問題的收斂,采用梯形分級加載[18]的形式施加內水荷載,迭代平衡以滲流場和應力場收斂為標志。 (1)襯砌受力損傷分析。當內水壓力小于80 m時,鋼筋和混凝土共同承擔內水壓力,二者協調變形,混凝土未出現損傷。隨著內水壓力增大至約165 m時,大部分混凝土進入塑性損傷狀態,混凝土內部微裂隙擴展,襯砌滲透能力增強,進而對滲流場和應力場產生影響。當內水壓力全部施加并迭代平衡后,由襯砌結構的損傷系數分布圖6可知,襯砌單元損傷量值在腰拱部位達到最大,進入損傷開裂階段,向頂部和底部逐漸減小,處于彈塑性損傷階段。分析計算過程可知,由于隧洞所在區域反演得到的地應力場側壓力系數較大,在開挖過程中,隧洞開挖邊界的圍巖在腰拱兩側損傷最為嚴重,承載能力較低,從而導致在滲流-應力耦合計算中襯砌在該處受力狀態更為不利,容易進入損傷開裂狀態。 圖6 襯砌結構損傷系數Fig.6 Damage coefficient distribution of lining (2)滲流場計算結果分析。通過三維滲流場計算,可得當內水壓力增大導致襯砌損傷開裂后滲流場的分布如圖7所示。由于鋼筋與混凝土的承載能力不同,在較大的拉力荷載作用下,襯砌混凝土單元不可避免的發生損傷及開裂,損傷狀態下的混凝土由于內部的微裂隙擴展導致滲透系數顯著增加,從而影響滲流場的分布。若假定襯砌滲透系數在計算過程中保持不變,計算得到的滲流場分布如圖8所示。對比可以看出考慮 圖7 損傷開裂階段的襯砌壓力水頭等值線圖(單位:m)Fig.7 Lining pressure head contour of damage cracking stage 圖8 不考慮損傷的襯砌壓力水頭等值線圖(單位:m)Fig.8 Lining pressure head contour without considering damage 損傷開裂后襯砌內的壓力水頭極差明顯減小,相應的水力坡降有所減小。這表明考慮損傷開裂后,襯砌所承擔的內水壓力降低,部分內水壓力由襯砌轉為圍巖承擔,圍巖內部的水力坡降增大。因此基于透水襯砌的設計原則,必須要注重圍巖的防滲抗滲性能處理,防止由于內水外滲導致區域圍巖產生滲透破壞。 (3)圍巖破壞區分析。將滲流場計算得到的滲透結點荷載作用于圍巖,得到考慮損傷開裂后圍巖的破壞區分布如圖9所示。圖10是假定滲透系數不發生改變時的圍巖破壞情況。可以看出,襯砌損傷開裂后,圍巖破壞范圍有所增加,尤其在襯砌損傷嚴重部位對應的圍巖破壞體積明顯增大。這說明基于透水襯砌的設計原則,圍巖承擔的內水壓力比重增大,其受力狀態更為不利,不考慮內水外滲的水工隧洞穩定計算偏于保守。 圖9 損傷開裂階段的圍巖破壞區分布圖Fig.9 Failure zones of surrounding rocks of damage cracking stage 圖10 不考慮損傷的圍巖破壞區分布圖Fig.10 Failure zones of surrounding rocks without considering damage (4)襯砌裂縫分析。迭代平衡時,滲流場的結點水頭收斂,無滲透荷載增量,襯砌的平均損傷系數和等效滲透系數也達到定值。此時,根據損傷開裂單元的應力數值和鋼筋的變形模量,可以近似計算出相應的襯砌裂縫寬度,考慮黏結滑移后的裂縫寬度約為0.153 mm,而不考慮黏結滑移效應時約為0.168 mm,表明考慮黏結滑移作用對減小構件的裂縫寬度有利,符合相應的物理實驗規律。分別計算兩種情況下混凝土的應變數值,考慮黏結滑移后混凝土的平均拉應變約為0.57×10-4,未考慮黏結滑移時混凝土平均拉應變約為0.69×10-4,可知黏結滑移提高了裂縫間的單元剛度,降低了裂縫間混凝土的平均拉應變,從而導致已有裂縫的鋼筋混凝土構件更不易產生新的裂縫,這與水工隧洞裂縫少而寬的分布特征相符。 (1)針對高水頭水工隧洞在內水壓力增大過程中襯砌單元的力學行為,將加載過程分為三個階段:線彈性階段、彈塑性損傷階段以及損傷開裂滑移階段,對處于不同加載狀態的襯砌單元采用不同的本構關系形式。 (2)采用間接耦合的方式實現滲流與應力的耦合計算,對處于三種加載狀態的單元引用突跳系數反映其滲透系數的變化。 (3)襯砌損傷開裂后,其內部的水力梯度明顯減小,圍巖承擔的內水壓力比例增大,證明了透水襯砌設計中圍巖是內水壓力的主要載體,因此在施工中要注重隧洞區域巖體的灌漿質量。 (4)考慮黏結滑移行為后,襯砌由于受拉剛化效應的存在,其裂縫寬度有所減小,裂縫間構件的剛度會提高,更不易產生新的裂縫。這符合水工隧洞在內壓增大至一定數值時,裂縫數量不再增加,但裂縫寬度增大,裂縫呈少而寬分布的特征。 □1.3 損傷開裂滑移階段
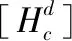
2 混凝土襯砌滲透損傷耦合計算
2.1 滲流場與等效節點荷載的數值解法
2.2 損傷開裂與滲流的耦合關系

3 工程實例
3.1 工程概況和計算條件


3.2 計算結果與分析

4 結 語

