某電站燈泡貫流式機組壓力脈動特性研究

姚 丹，馬 彪，李正貴

(1. 國際小水電中心，杭州 310002； 2.流體及動力機械教育部重點實驗室—西華大學，成都 611730)

1 概 述

黃河干流某電站安裝4臺燈泡貫流式機組，單機額定出力24.67 MW，額定流量399.7 m3/s，額定轉速68.18 r/min，具有4個槳葉(可調)和16個活動導葉。該電站自運行以后，機組出現了較嚴重的水壓力脈動甚至水力振動問題，以致多次發生諸如轉輪室裂紋、發電機轉子支架裂紋等損壞現象。

對于水輪機組的壓力脈動問題，即水輪機轉輪內部的非定常流動問題，國內外學者已有較多的研究。錢忠東等[1]采用大渦模擬方法，分析了貫流式水輪機在不同工況下的壓力脈動特性，發現額定工況下，轉輪出口振幅最大；小流量工況下，尾水管內振幅最大。李萬等[2]研究了不同湍流模型對尾水管偏心渦帶的影響，發現SST模型的適應性及模擬結果與試驗的吻合度均為最佳。姚丹等[3]結合模型試驗，闡述了水輪機模型壓力脈動的測試原理及方法。Sudsuansee等[4]對燈泡貫流式水輪機進行了非定常計算，對前緣空化及轉頻進行了分析。Luo等[5]對雙向潮汐電站燈泡貫流式水輪機受重力影響下的4種運行工況壓力脈動特性進行了分析。鄭源等[6]提出混流式水輪機運行不穩定的重要原因是尾水管內的壓力脈動，總結了減小或消除尾水管渦帶的有效措施。王正偉等[7]針對混流式水輪機的典型部分負荷工況，計算了尾水管內部由于渦帶引起的不穩定流場，得到了尾水管不同部位的壓力脈動對轉輪內壓力的影響。現有研究成果表明在某些工況下，貫流式機組會發生振幅較大的壓力脈動，但燈泡貫流式壓力脈動的內部機理以及外在表現形式還缺乏深入的研究。本文基于模型、真機試驗以及CFD數值模擬方法，對黃河某干流某燈泡貫流式水輪機組進行了壓力脈動問題研究，分析了水輪機內部的壓力脈動特性，揭示機組壓力脈動的產生機理，并分析產生轉輪室裂紋的原因。

2 研究內容

2.1 研究工況及試驗測點設置

在電站裝置空化系數下選取水頭為8 m，槳葉開度為31°、34°、37°、40°四個角度所對應的協聯工況點進行壓力脈動的試驗和計算。壓力脈動的實驗測點設置在距離轉輪出口約0.4倍轉輪直徑處[8]，如圖1所示。

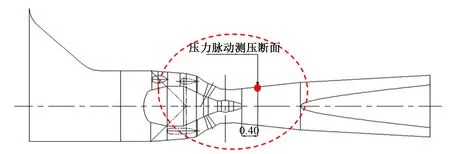
圖1 壓力脈動測點Fig.1 Location of the pressure survey point

2.2 壓力脈動的大小

壓力脈動的大小，通過壓力脈動幅值ΔH/H來表示。ΔH/H是壓力脈動波形的雙振幅值的峰值ΔH與試驗水頭H的比值[9]，其中ΔH按97%的置信概率選取，如圖2所示。

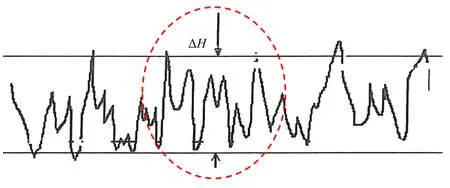
圖2 壓力脈動雙振幅示意圖Fig.2 Schematic diagram of the pressure double amplitude

2.3 壓力脈動的頻譜

利用快速傅里葉變換將復雜的振動分解，將時域轉化到頻域，通過頻域圖中分解后的頻譜值，特別是第一主頻值f1，可找到引起振動的原因[10]。為研究方便，特定義轉頻X=n/60=68.18/60=1.136 Hz，其中，n是額定轉速。本文后述的mX即表示m倍的轉頻頻率。

3 研究方法

3.1 模型試驗簡介

在燈泡貫流式機組模型試驗臺(如圖3所示)上，對機組模型轉輪進行壓力脈動試驗。同步采樣各測試通道信號，記錄時域上的模擬信號波形圖，應用軟件調用FFT分析處理模塊對信號進行頻譜分析，確定壓力脈動的頻譜特性[9]。

圖3 燈泡貫流式模型試驗臺Fig.3 Bulb tubular turbine model test stand

3.2 真機試驗簡介

利用電站機組狀態監測及跟蹤分析系統平臺(如圖4所示)，對電站真機進行壓力脈動試驗。安裝在機組尾水管的傳感器和變送器將壓力脈動物理信號轉化為電信號，傳送到相應機組的信號采集及預處理單元，得到反映機組壓力脈動的特征參數、曲線和圖表等，統一存儲到系統平臺的狀態數據服務器上[11]。

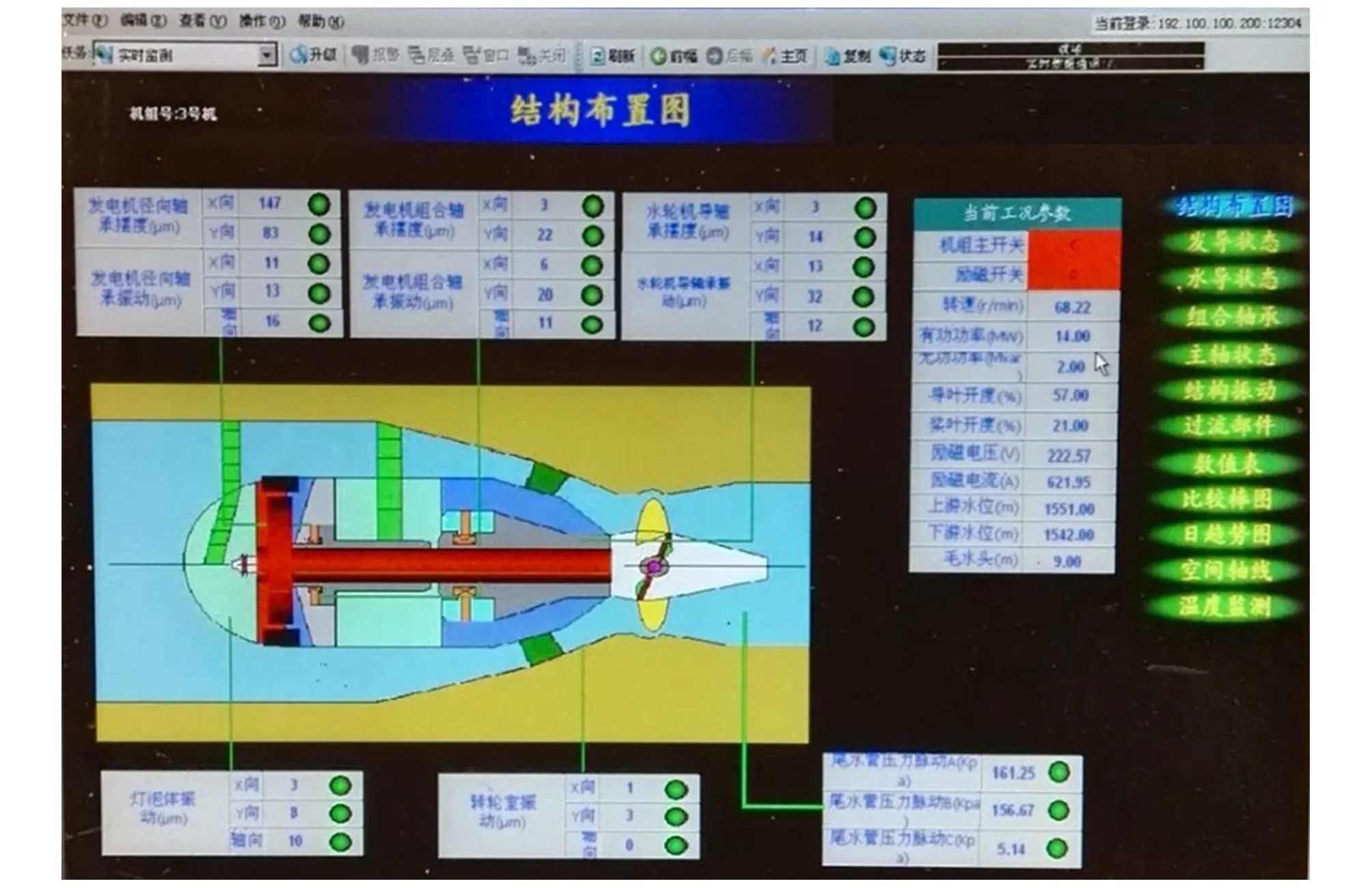
圖4 機組狀態監測及跟蹤分析系統平臺Fig.4 Stability monitoring and tracking analyzing system

3.3 CFD數值模擬計算

運用CFD數值原理對水輪機進行模擬仿真試驗，建立與真機對應的三維流體域幾何模型(如圖5所示)，采用分塊網格技術將整個子區域(進水流道、導葉、葉片、尾水管)分別進行網格劃分[12]，前流道和尾水管結構較規則，采用六面體結構化網格，而導葉和葉片是由相對復雜的不規則曲面構成的部件采用四面體非結構化網格，且對近壁面等關鍵部位進行了局部網格加密，最終將各網格子單元按照模型的順序嵌套為整體網格，如圖6所示。

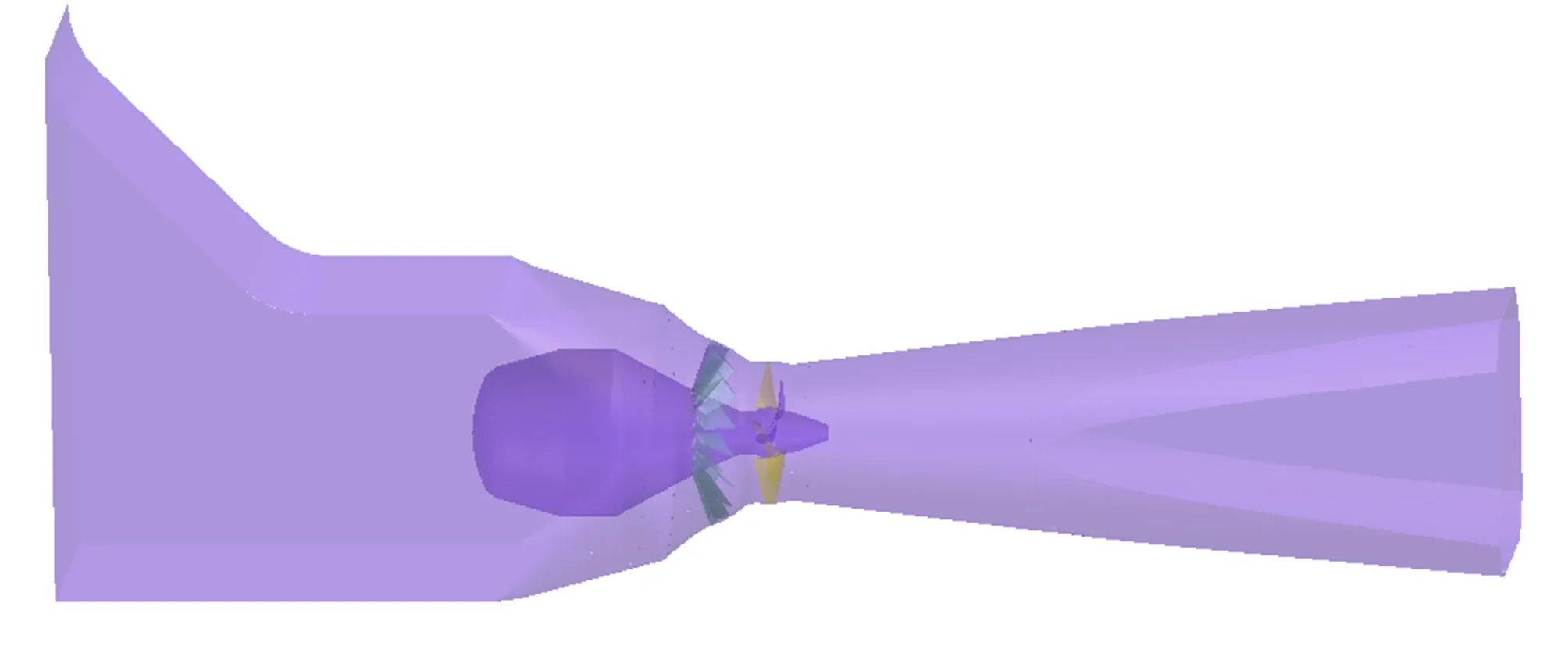
圖5 幾何模型Fig.5 Geometric model

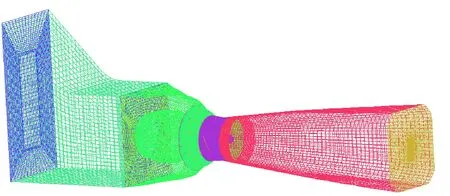
圖6 網格模型Fig.6 Mesh model

(1)網格數量的選取。隨著計算網格數量的增加，計算精度提高。當網格數量在982萬左右時，網格數量對計算結果的影響較小，外特性接近于真實情況。通過網格無關性驗證，本文計算取982萬個網格進行計算。

(2)邊界條件的選取。取流體模型的進口邊界為質量流量邊界，出口邊界為給定靜壓力邊界。當壁面靜止時，設置成壁面無滑移條件；當壁面平移或者旋轉時，通過給出壁面切應力模擬壁面滑移。在動、靜交界的耦合面設為滑移網格交界面[13]。采用SIMPLEC算法實現壓力和速度的分離求解[14]。

(3)計算湍流模型的選取。鑒于燈泡貫流式水輪機的轉輪、導葉、流道有較多曲面，會帶來大曲率流動。為了準確地模擬這種流動，本文選用如下RNGk-ε湍流模型[15]。

RNGk-ε模型k和ε的輸運方程分別為：

(1)

(2)

修正后的有效黏性系數μeff在高雷諾數時，有：

(3)

在ε方程中增加了R項，R項為：

(4)

式中：η=Sk/ε，η0=4.38 ，β=0.012。

通過修正的k、ε兩項得到新的輸運方程為：

(5)

(6)

(7)

各湍流模型常數分別為：

Cμ=0.084 5，Cε1=1.42，Cε2=1.68，σk=0.72，σε=0.75

(4)時間步長的選取。時間步長Δt按下式計算：

(8)

其中：n為轉速；nr=2，即每隔2°計算一次；Δt單位為r/min。

(5)計算收斂標準。迭代計算的收斂標準以殘差值來衡量，默認的殘差值為1×10-4。

4 研究結果

本文上述的模型試驗、真機試驗以及CFD數值模擬計算的主要結果，分別見圖7～圖9。其中，分別給出了4種不同槳葉角度運行工況下的機組壓力脈動時域、頻域圖。

模型試驗各工況的時域及頻域圖見圖7。真機試驗各工況的時域及頻域圖見圖8。CFD試驗各工況的時域及頻域圖見圖9。對模型試驗、真機試驗以及CFD數值計算結果的時域及頻域圖(圖7～圖9)中的壓力脈動幅值以及第一主頻進行統計分析，可得表1和圖10。CFD數值模擬的各工況尾水管渦核見圖11。

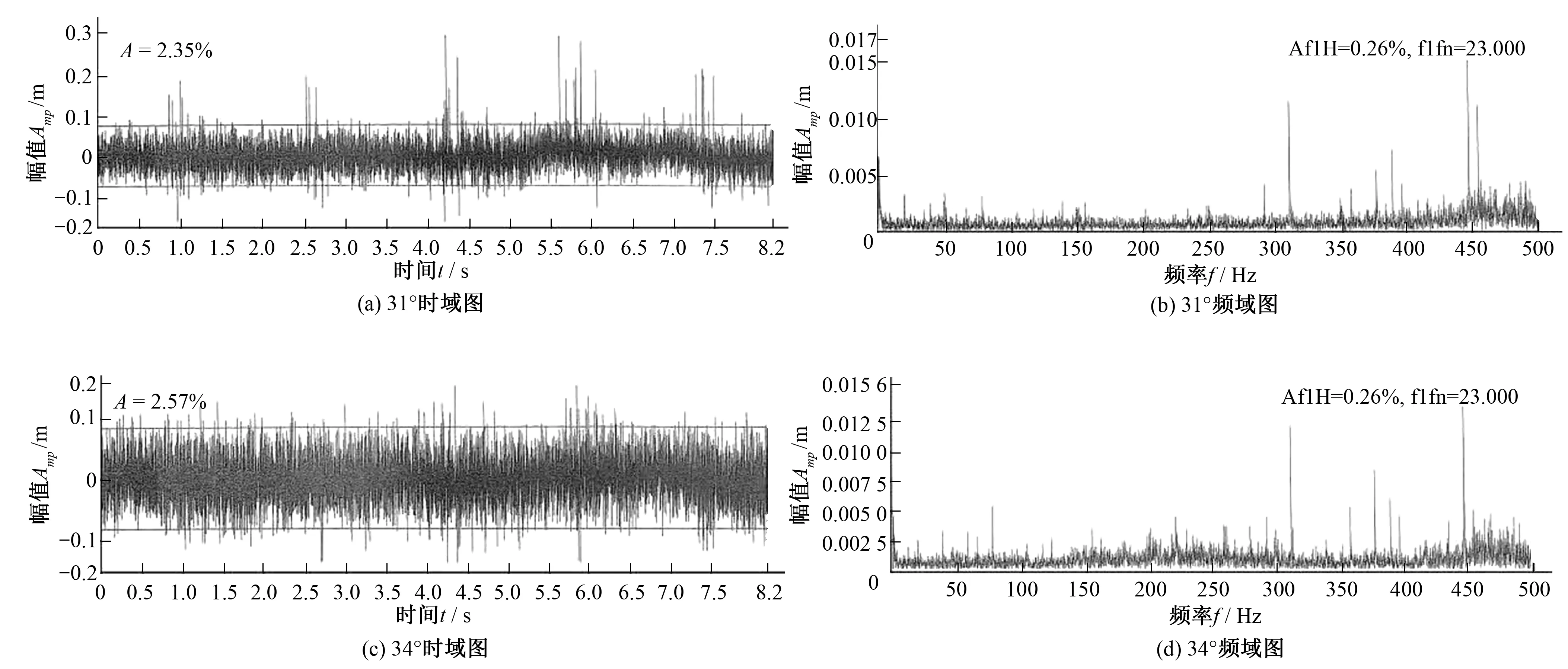
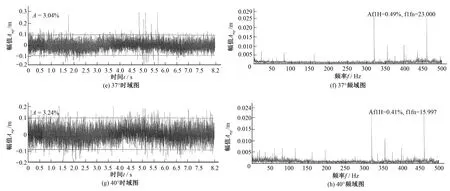
圖7 模型試驗各工況的時域及頻域圖Fig.7 Time domain chart and Spectrum chart for various working conditions in model test

5 結果分析

5.1 壓力脈動的幅值

由圖10可知，模型試驗、真機試驗、CFD數值計算結果，在所選擇的工況范圍內，隨著槳葉開度的增大，脈動幅值相應增大。但同一槳葉開度對應的脈動幅值略有不同，CFD結果最小，真機試驗結果最大。

5.2 引起壓力脈動的原因

由于本電站機組導葉數Z0=16，轉輪葉片數Z1=4，轉速n=68.18 r/min，可知導葉數z0與轉輪葉片數Z1的最大公約數K=4。

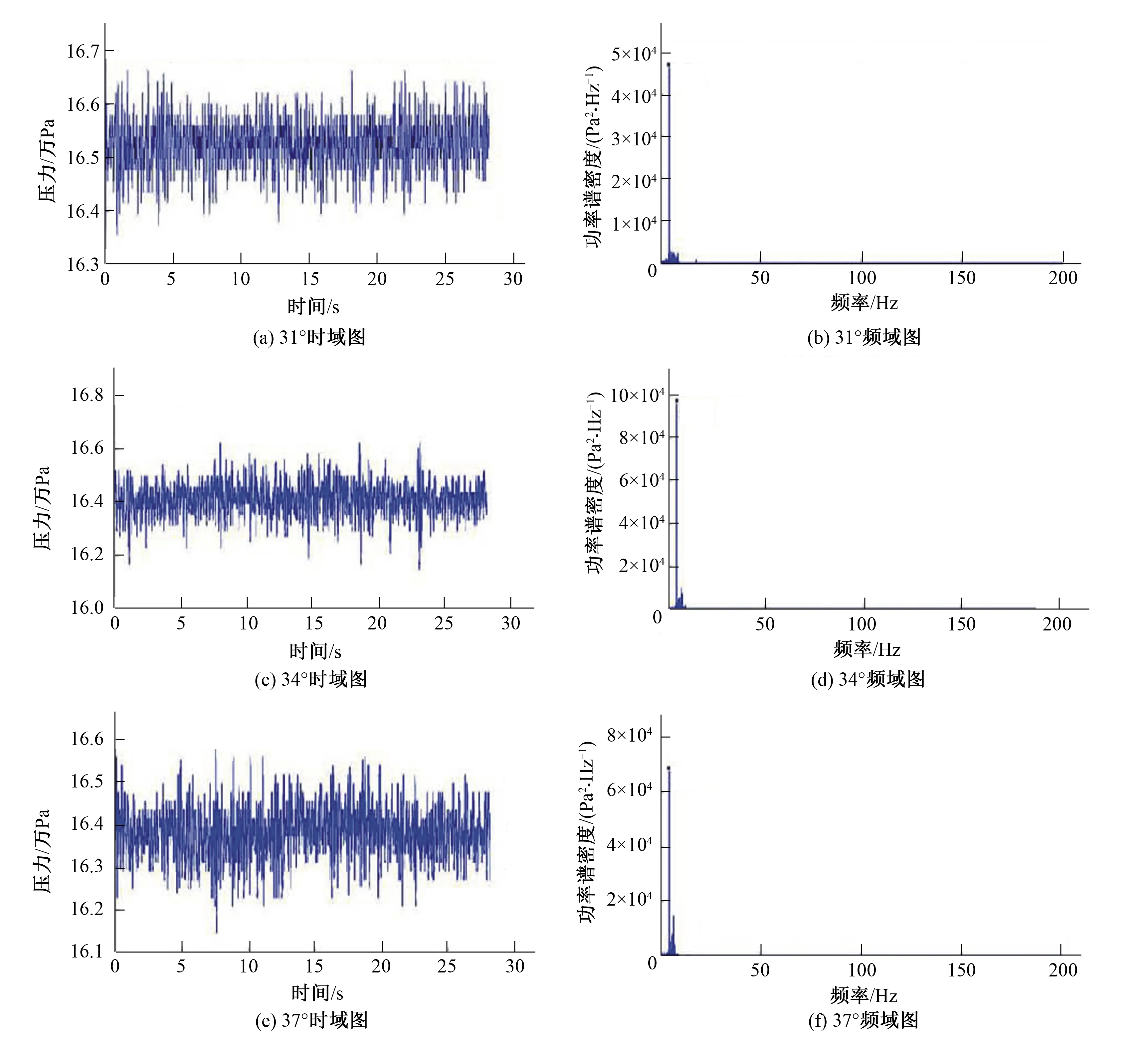
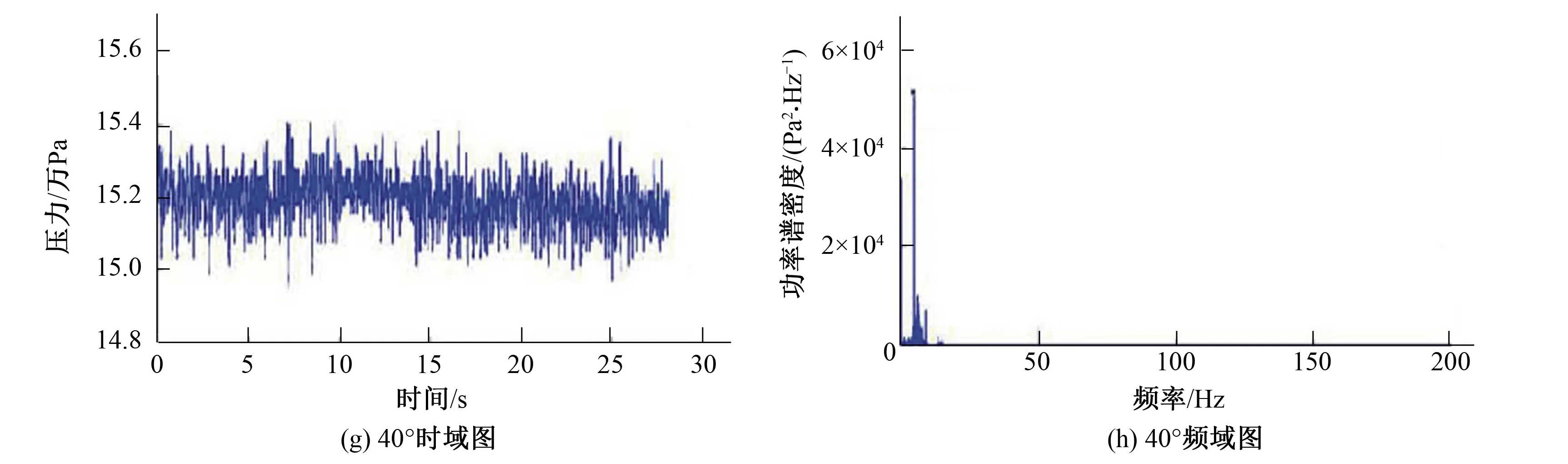
圖8 真機試驗各工況的時域及頻域圖Fig.8 Time domain chart and Spectrum chart for various working conditions in prototype test

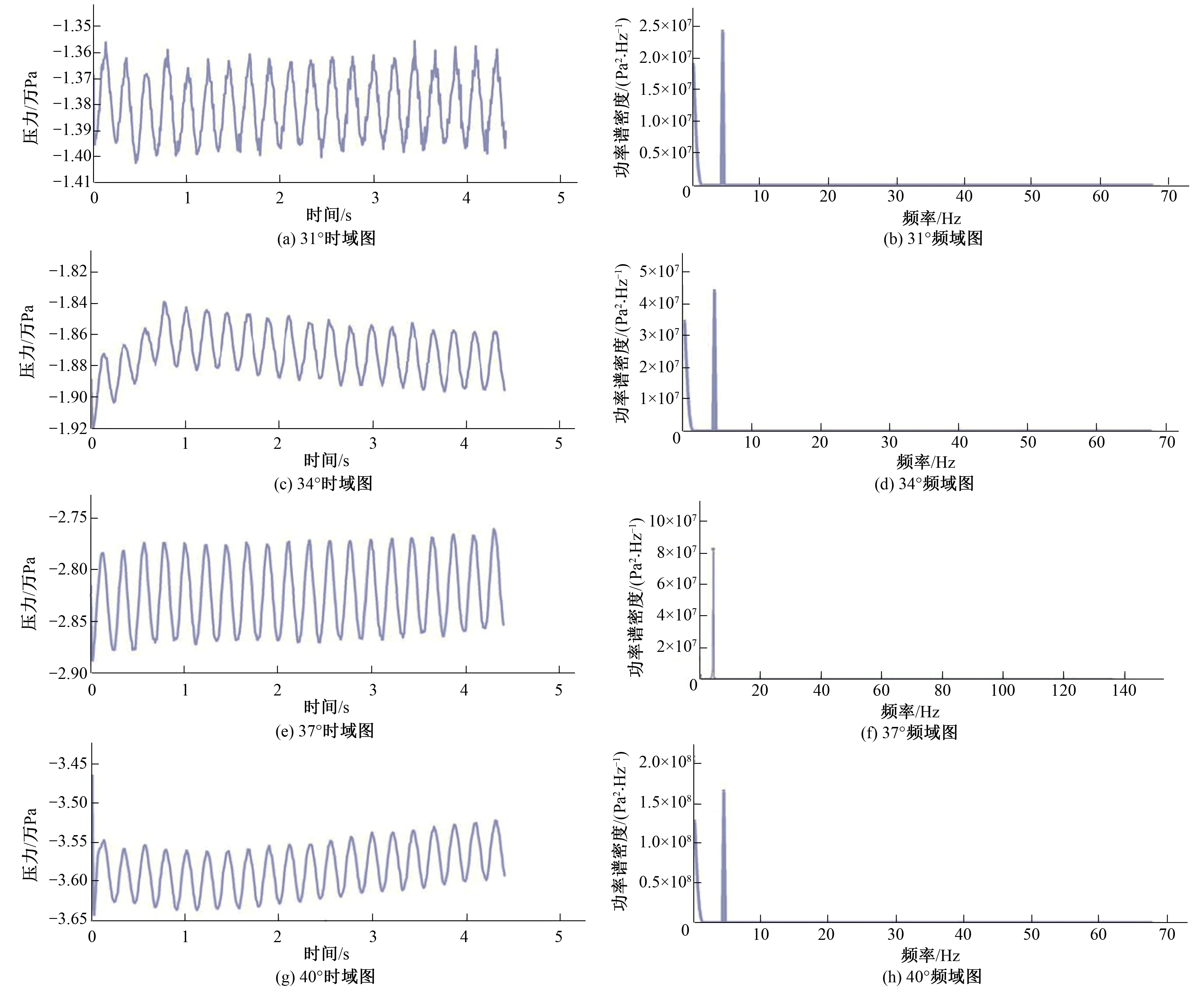
圖9 CFD試驗各工況的時域及頻域圖Fig.9 Time domain chart and Spectrum chart for various working conditions in CFD test

由表1可知，模型試驗中壓力脈動的第一主頻值與真機試驗、CFD計算結果有所不同，當槳葉開度為31°、34°、37°時，模型壓力脈動第一主頻都為23X，主要是由流場的不穩定流動；當槳葉開度為40°時，第一主頻16X與由導葉、葉片和機組旋轉疊加引起的理論計算的動靜干涉頻率值(表2)一致，因此，40°時的模型壓力脈動是由導葉、葉片和機組旋轉疊加造成的動靜干涉所致。

由表1可知，在所選的工況中，真機試驗、CFD計算的壓力脈動的第一主頻值為4X，與理論計算的動靜干涉頻率值(表2)完全一致。因此，真機壓力脈動是由轉輪旋轉引起的動靜干涉所致。

5.3 壓力脈動呈現的渦核形式

由圖11可知，對應4個不同槳葉開度的真機壓力脈動均由轉輪旋轉引起的動靜干涉所致，但其內部尾水管的渦核形式

表1 三種方法在不同工況下的壓力脈動的幅值及第一主頻Tab.1 Amplitude and first main frequency

表2 引起壓力脈動的部分原因及頻率公式Tab.2 Some causes of pressure fluctuation and frequency formula

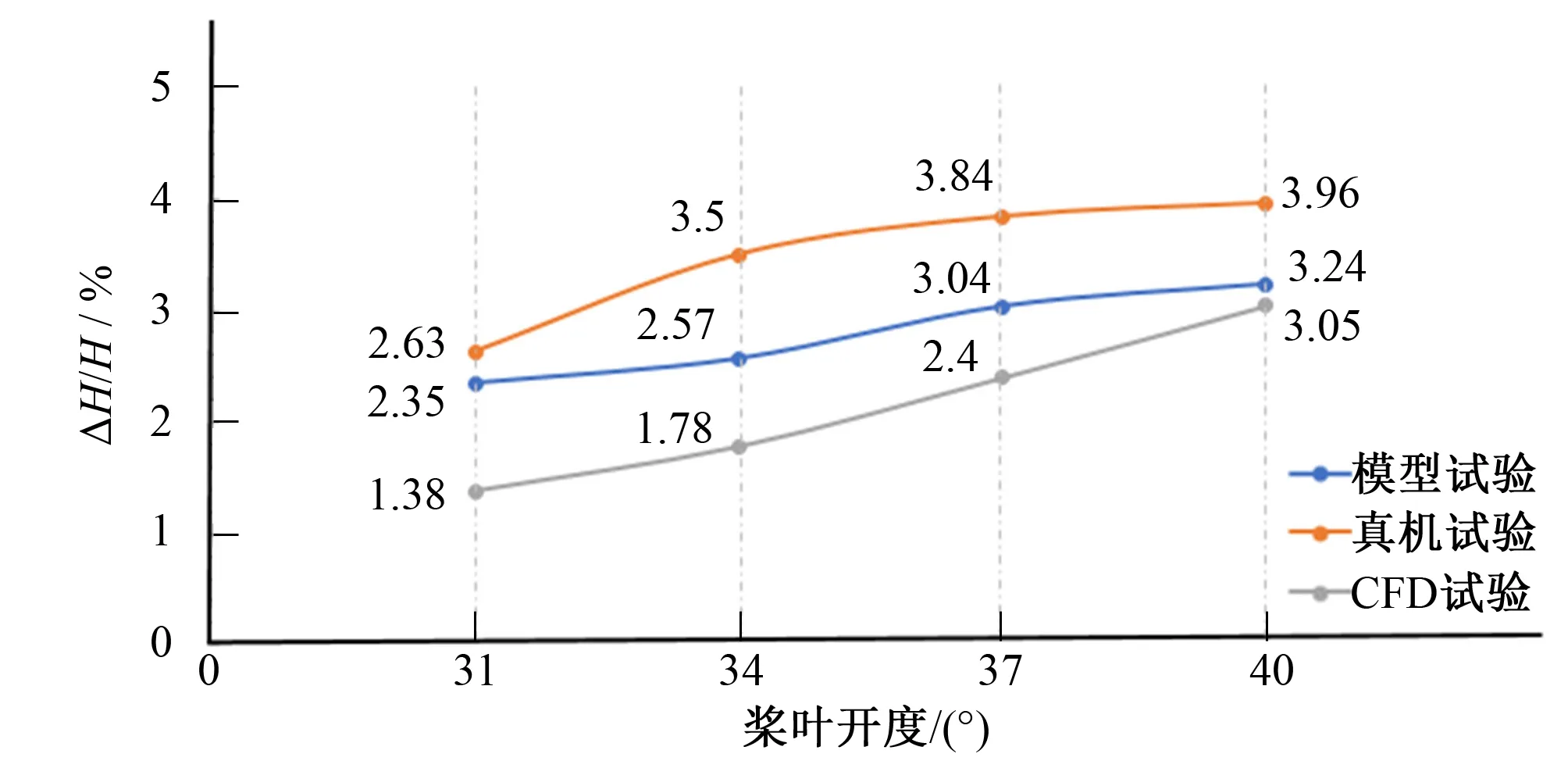
圖10 壓力脈動幅值隨開度的變化曲線Fig.10 Change curves of amplitude varies with opening degree

圖11 CFD數值模擬的各工況尾水管渦核Fig.11 Draft tube vortex for various working conditions in CFD test

卻不盡相同。尾水管漩渦的轉向與轉輪旋轉的方向一致，渦核的旋轉中心為尾水管中心線，并未發生偏心現象，渦核區域主要集中在尾水管中心軸線區域，以及尾水管的外壁，漩渦的流向是從轉輪沿著流道中心流入尾水管，并由尾水管進口向下游流出。

槳葉開度31°工況的尾水管中心渦核繞自身軸線逆時針旋轉，外壁渦核構成一個渦環，中心形狀可對稱地分為四部分，尾水管中心渦核外部環繞著四個對稱的離散渦核，很明顯與四個葉片的尾跡流有關；34°工況的尾水管中間的渦鼓是水流繞流泄水錐所致，外壁的漩渦是由于轉輪出口速度的圓周速度分量所導致；37°工況所呈現的形式與34°工況類似；40°工況的尾水管渦核無明顯的四部分渦帶，渦核呈現轉輪整體旋轉形式。

5.4 產生轉輪室裂紋的誘因分析

由于真機試驗、CFD試驗壓力脈動的第一主頻值為4X(葉片數乘以轉頻)，可知機組在運行時，水流在轉輪室隨著轉輪的旋轉而做復雜的空間運動，有一部分水流從葉片輪緣和轉輪室之間的縫隙穿過，而這部分的水流壓力很低但速度很高，呈射流狀，即“狹縫射流”。轉輪室的部分區域在轉輪葉片經過的時候，受到由射流狀水流的作用而產生低壓的水壓力；當葉片轉過此區域時，轉輪室的這部分區域又承受壓力較高的水壓力。這樣隨著機組轉輪的旋轉，轉輪室受到的水壓力在低壓和高壓之間循環往復的變換，產生頻率為葉片數乘以轉頻的振動，最終導致轉輪室部分區域出現疲勞，產生貫穿性裂紋。

6 結 語

針對某電站機組的4個不同槳葉開度的運行工況，經模型試驗、真機試驗以及CFD數值模擬計算結果的對比分析，對于燈泡貫流式機組的壓力脈動特性，得出以下結論。

(1)壓力脈動幅值隨著槳葉開度的增加而增大。

(2)真機壓力脈動是由轉輪旋轉引起的動靜干涉所致；模型機組壓力脈動主要是由流場的不穩定流動導致，個別工況的壓力脈動是由導葉、葉片和機組旋轉疊加造成的動靜干涉引起。

(3)各工況下引起真機壓力脈動的原因一致，但壓力脈動的渦核形式卻不盡相同。

(4)導致轉輪室裂紋的誘因為狹縫射流產生的疲勞破壞。

□