徑向導葉式潛水泵內部流動與非定常特性研究

王成斌，金 雷，張 帥，謝 磊，王 勇,3

(1.江蘇大學國家水泵及系統工程技術研究中心，江蘇 鎮江 212013；2.合肥恒大江海泵業股份有限公司，合肥 231131；3.江蘇大學鎮江流體工程裝備技術研究院，江蘇 鎮江 212009)

0 引 言

徑向導葉式潛水泵屬于多級泵的范疇，具有揚程高，體積小等優點，被廣泛用于農村灌溉、礦井排水等領域。對于離心泵，尤其是低、中比轉速離心泵而言，其軸功率隨著流量的增加而連續上升[1]，在大流量工況下容易出現過載，這種現象在徑向導葉式潛水泵中更為常見。另一方面，為了響應國家“節能減排”的號召，人們對于泵的效率與穩定性等方面越來越重視，針對徑向導葉式潛水泵的研究具有較高的實用價值。

隨著計算流體力學的發展，越來越多的學者和研究人員采用數值計算方法對潛水泵進行研究[2-5]。數值計算可以較準確地預測水力性能，對完善泵設計理論以及提高設計水平也有著重要意義。張憶寧[6]基于數值計算，對兩級潛水泵進行了優化設計，最終選取了葉輪葉片數Z=3，葉片出口角β2=12°的方案。崔寶玲等[7]基于CFD數值模擬，對多級潛水泵的效率進行了優化，優化后的模型效率提高了4.12%，單級揚程提高1.449 m。程效銳等[8]以5級井用潛水泵為研究對象，通過改變導葉出口邊位置提高了泵的效率和揚程。曹衛東等[9]結合正交試驗設計法與數值技術對導葉不同的兩級離心泵進行了研究，得到了較優方案，其揚程和效率分別提高1.24m和4%。施衛東等[10]采用數值模擬與性能試驗相結合的方法，驗證了等比例縮放法在潛水泵的應用。李文全等[11]基于FLUENT對井筒式潛水軸流泵出水管道進行了數值研究，獲得了進水口流量對出水管道水力特性的影響規律。Boncinelli等[12]通過數值計算得到潛水泵在不同導葉結構下的性能，從而確定導葉性能較優時的相關參數。葛明亞等[13]設計了9組不同的潛水模型泵，并與原型泵進行了數值模擬對比分析，得到了泵性能最優時的葉輪和導葉葉片數匹配方案。

目前對徑向導葉式潛水泵的內流及非定常特性的研究相對較少。本文以一臺單級徑向導葉式潛水泵為研究對象，對其內部流場、葉輪徑向力、軸向力以及壓力脈動等特性進行分析，以期為潛水泵的優化設計提供借鑒。

1 計算模型與計算設置

1.1 計算建模

本文所選用的研究對象為單級徑向導葉式潛水泵，介質為常溫清水，潛水泵結構如圖1所示；主要設計參數為流量Qd=100 m3/h，揚程Hd=21 m，轉速nd=1 450 r/min；比轉速ns=76.6。葉輪的主要參數如下：進口直徑D1=125 mm，出口直徑D2=300 mm，出口寬度b2=13，葉片數Z=4；另外正、反導葉的葉片數都為7。

采用Creo2.0軟件對計算域水體進行三維造型，為了克服邊界條件對內部流場的影響，分別在進口處加水槽，在出口處進行了延長。其中水槽為柱體，外徑為葉輪進口直徑的8倍，出口段長度為出口直徑的3倍。圖2為計算域水體圖，從左到右依次為出口延長段、反導葉、正導葉、葉輪、進水段、水槽。

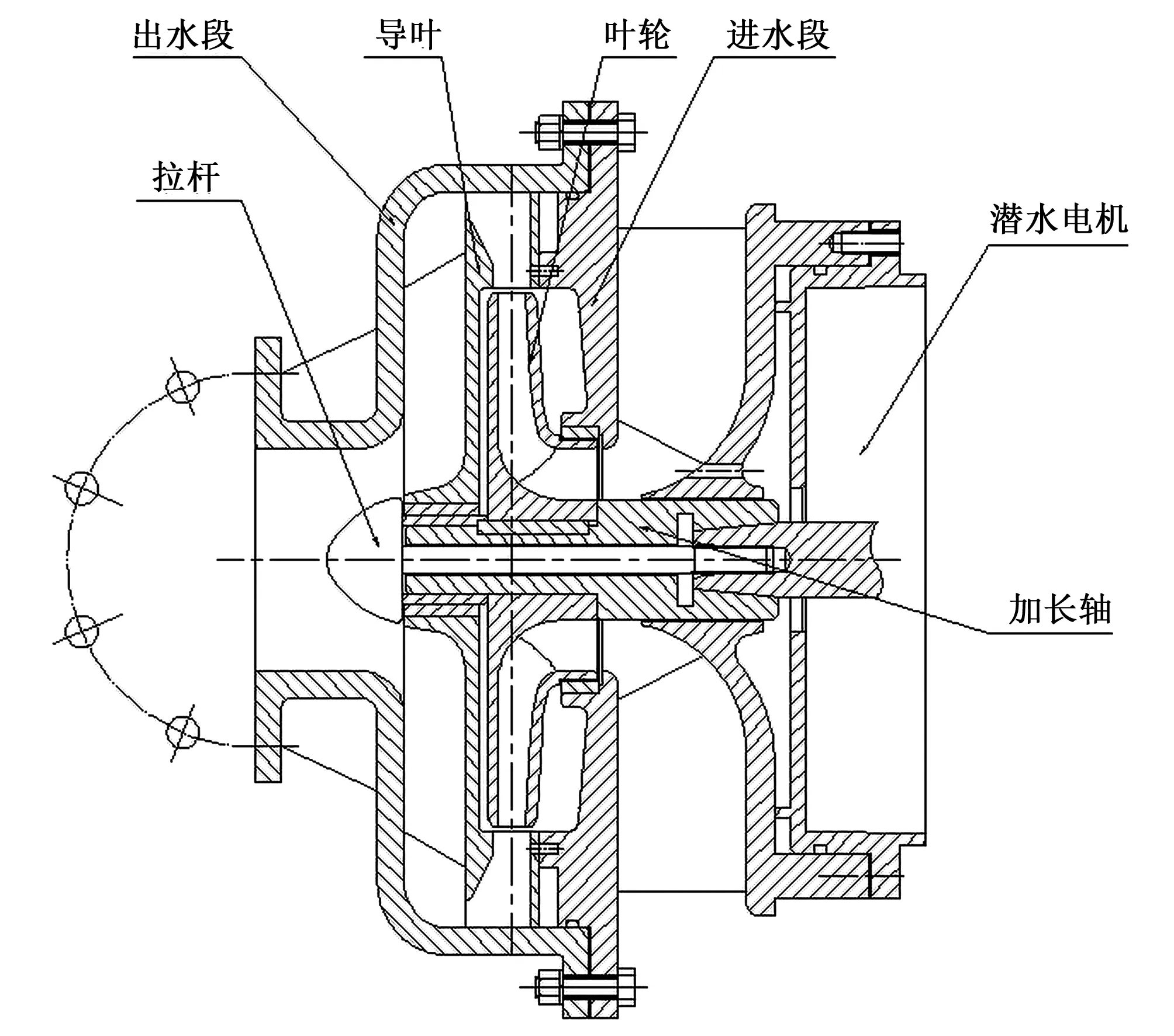
圖1 泵結構示意圖Fig.1 Pump structure diagram

圖2 計算域水體Fig.2 Water body of calculation domain

1.2 計算設置

1.2.1 網格劃分及網格無相關性分析

采用ICEM CFD軟件對計算域水體進行網格劃分。為了獲得更準確的計算結果，縮短計算時間，同時考慮葉輪的后續優化設計，現葉輪水體采用四面體非結構化網格，其余計算域水體采用六面體結構化網格。同時為了選取合適的網格數，需要對網格進行無關性檢驗。本文通過調節重要計算面拓撲線上的網格節點數，在CFX前處理設置完全相同的前提下，得到了5套不同網格數的網格，并以模擬揚程為評價標準評判，如表1所示。

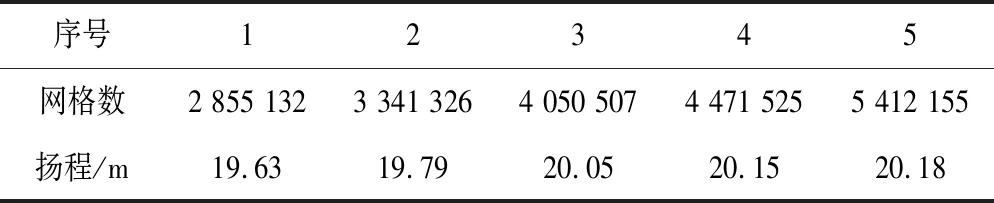
表1 網格無關性檢查Tab.1 Inspection of grid independence

由表1中可以看出，隨著網格數的逐漸增加，揚程的計算值逐漸趨于穩定。其中網格數方案4和方案5中的揚程計算結果較為接近，這說明再增加網格數對數值計算的結果影響很小。同時考慮到計算機的運算時間以及其運算能力，確定方案4為本文的計算網格方案。圖3是所確定的各計算流體域的網格。

圖3 網格劃分Fig.3 Mesh generation

1.2.2 控制方程

在離心泵數值計算中所需的控制方程包括質量方程、動量方程以及能量方程。本文中流體介質為清水，是不可壓縮介質，只需滿足質量方程和動量方程[14]。

(1)質量守恒方程：

(1)

(2)動量守恒方程：

(2)

式中：ρ為流體的密度，kg/m3；u為流體速度，m/s；x為空間坐標，i，j為不同方向分量；μ為流體動力黏度，Pa.s；Si為源項。

1.2.3 CFX數值計算設置

采用ANSYS CFX軟件進行潛水泵的數值計算，將葉輪水體設置為旋轉域，其余水體均設置為靜止域。定常計算時，葉輪與其他部件的動靜交界面采用凍結轉子模型；非定常計算時，動靜交界面采用瞬態動靜轉子模型。

本文采用對高應變率及流線彎曲程度較大的流動有較好自適應性的RNGk-ε湍流模型。邊界條件采用壓力進口和質量流量出口邊界條件組合，進口設置為總壓1 atm，出口處的質量流量的數值根據流量計算得到。固壁處設置為無滑移壁面，近壁處采用Scalable壁面函數。

定常計算時，控制方程的對流離散項采用二階高精度，將平均殘差值RMS作為計算收斂依據，設置收斂精度為10-4。非定常數值計算以定常計算結果作為初始值，時間步長設置為1.149 4×10-4s，即葉輪每旋轉1°計算一次，葉輪共計算6圈，最后一圈的數據用于本文的分析。

2 外特性計算結果及試驗驗證

為了驗證數值計算的準確性，在江蘇大學流體中心實驗室的開式試驗臺上進行試驗，試驗臺如圖4所示。得到了不同工況下外特性的試驗值，并與模擬值進行對比，如圖5所示。

由圖5可以看出，數值計算得到的性能曲線與試驗值變化趨勢相同。在設計流量下，揚程的計算值為20.15 m，與試驗值的偏差為2.6%；效率的計算值為75.42%，與試驗值的偏差為1%。除卻大流量工況(流量大于1.2Qd)，效率計算值在1.2Qd工況下的偏差最大，為4.7%，揚程計算值在0.6Qd工況下的偏差最大，為6.4%。可以看出在流量不超過1.2Qd時，對于潛水泵的計算是較為準確的；對于大流量工況下計算不準確在下文中會進行分析。同時可以看出，該潛水泵的功率曲線在大流量工況下趨于平緩，有較好的無過載性能。基于較為準確的計算結果，選取三個典型工況(0.8Qd、1.0Qd、1.2Qd)進行潛水泵內流分布、徑向力、軸向力和壓力分布分析。

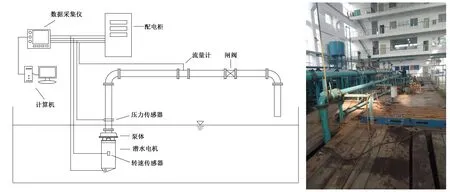
圖4 試驗裝置圖Fig.4 Diagram of test bench

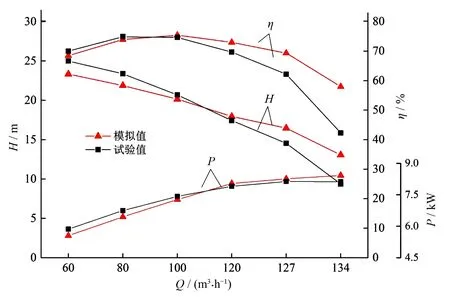
圖5 計算與試驗結果對比Fig.5 Comparison between calculation and experiment

3 計算結果分析

3.1 內流場分析

選取潛水泵的葉輪出口所在的中間截面為基準面，對潛水泵的主要部件葉輪和導葉的靜壓分布、速度分布進行分析。選取的中間截面如圖6所示。

圖6 中間截面示意圖Fig.6 Midsection diagram

(1)靜壓分布云圖。圖7分別是3個工況下，葉輪和導葉在基準面處的靜壓云圖。從圖7可以看出，在不同的流量下壓力都呈現出從葉輪進口到正導葉出口(過渡段)逐漸增大的規律。其中，在葉輪進口處壓力最低，隨著流量的增加進口低壓區面積逐漸增大。在1.2Qd工況下葉輪流道在稍微偏離進口處存在極低壓區，結合圖5在流量大于1.2Qd時揚程、效率的計算值與試驗值偏差較大，可以考慮在大流量工況下發生了汽蝕；正是由于空泡的出現，泵內的流動變得復雜，損失加劇，導致揚程下降幅度較大。在0.8Qd工況下，在葉輪出口處及正導葉內的流道壓差比較大，液流不穩定，隨著流量的增加，該處壓差逐漸減小，液流逐漸穩定。在0.8Qd與1.2Qd工況下，正導葉流道與導葉過渡段流道內存在著兩種較為穩定的壓力量級，其中0.8Qd工況下的壓力分別高于1.2Qd工況下的壓力，這與小流量下的揚程高于大流量下的揚程相對應。整體而言，設計工況下葉輪與導葉流道的壓力梯度較小，這也說明了額定工況下的潛水泵的內流比較穩定，其損失較小。

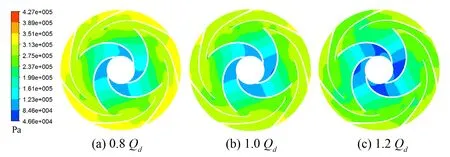
圖7 基準面靜壓分布云圖Fig.7 Static pressure distribution in midsection

(2)速度分布與流線圖。圖8給出了在基準面處的葉輪和導葉的速度分布與流線圖，其中葉輪中的速度為相對速度。從圖中可以看出，不同流量工況下，葉輪和導葉流道內均出現不同大小的低速區。對于葉輪，低速區均出現在各個流道的靠近葉片的工作面處，從進口覆蓋到約半個葉片。葉輪流道的低速區面積在小流量工況下很明顯，隨著流量的增加，低速區面積越來越小，至1.2Qd工況時已經幾乎消失；葉輪流道葉片背面處速度相對較大，且隨著流量的增加該處的速度逐漸增大。對于導葉，流道中出現大面積的低速區，結合圖7可以看出正導葉起到了動能轉化為壓力能的作用。在0.8Qd工況下低速區面積最大，以至于幾乎充滿整個流道，隨流量增加，低速區面積逐漸減小，并且低速區偏向于正導葉流道的右側葉片處。從流線圖看出，在較低流量下，在葉輪出口靠近正導葉葉片處、正導葉流道與過渡段內均存在漩渦及回流，流動紊亂；在設計流量下流動最穩定，除了個別正導葉有漩渦外，只有在過渡段流道內存在尺寸較小的渦；至較大流量工況下，導葉內的渦增多，過渡段每個流道內依舊存在大小不一的渦。由此可見，過渡段內的流動復雜，損失很大，相對而言，設計工況下的流動較穩定，與效率最高相對應。

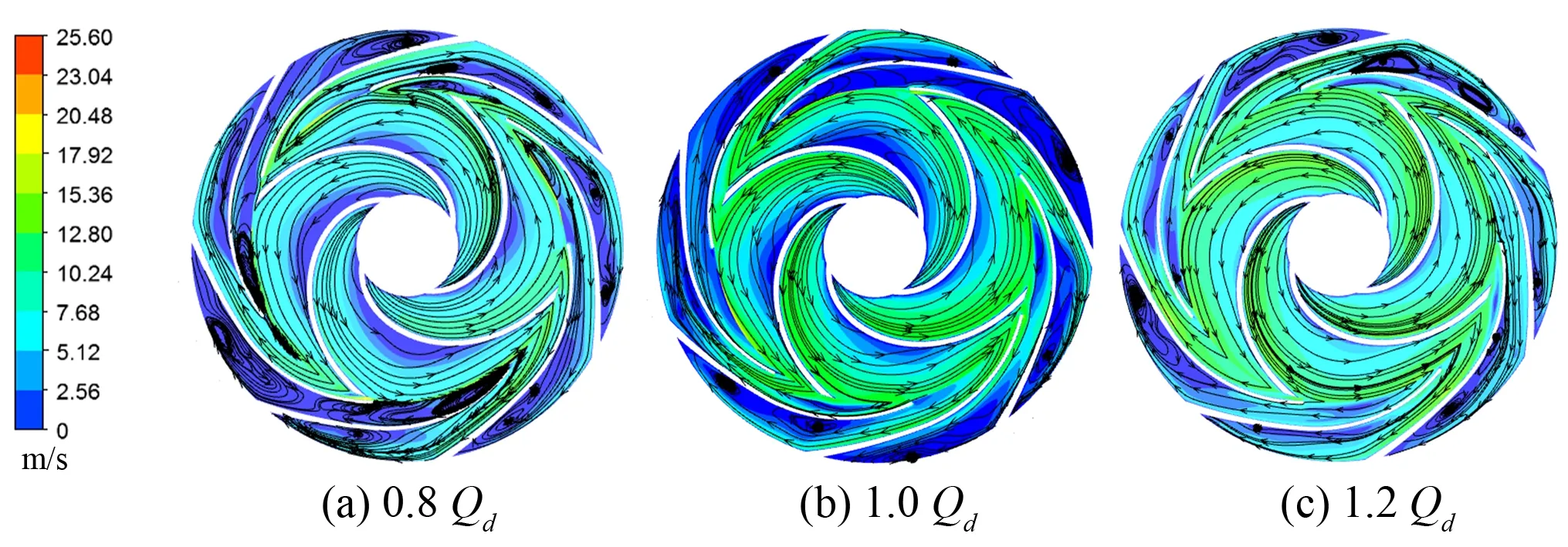
圖8 基準面速度分布與流線圖Fig.8 Velocity distribution and streamline in midsection

3.2 徑向力與軸向力分析

葉輪是泵的旋轉部件，其性能對泵的穩定性有很大的影響，接下來對潛水泵葉輪在典型工況0.8Qd、1.0Qd、1.2Qd下的徑向力與軸向力進行分析。

(1)葉輪的徑向力。圖9是潛水泵的葉輪在不同工況下的徑向力時域圖。可以看到在不同工況下，葉輪的徑向力都是圍繞一基準水平線(平均徑向力)上下有規律的波動。三個工況下，葉輪在一個旋轉周期內所受的徑向力都出現28個波峰與波谷，考慮到葉輪葉片數為4，導葉葉片數為7，說明葉輪和導葉的動靜干涉對徑向力脈動有較大影響。設計工況下的平均徑向力最小，0.8Qd工況下次之，1.2Qd工況最大，其分別為34 N、39 N與67.6 N。隨著流量的增加，葉輪所受徑向力的波動幅度逐漸增加。

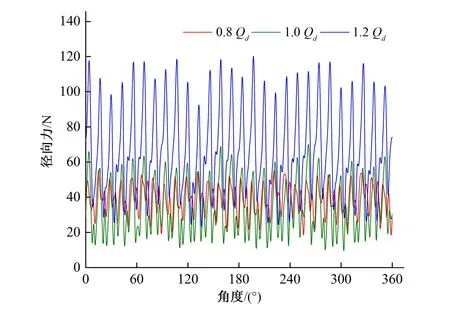
圖9 葉輪徑向力時域圖Fig.9 Time domain diagram of impeller radial force

圖10是不同工況下葉輪的徑向力分布矢量圖，其中橫、縱坐標分別代表葉輪徑向力在中間截面上相互垂直方向的分力。可以從圖中看出，三個工況下葉輪徑向力的矢量圖都呈現出四角星狀分布，這與葉輪的葉片數為4相對應。在0.8Qd工況下，矢量圖近似于一個中空的正方形，說明在該工況下徑向力變化比較穩定。設計工況下的徑向力極值大小與0.8Qd工況相近，1.2Qd工況下徑向力明顯大于其他兩個工況。

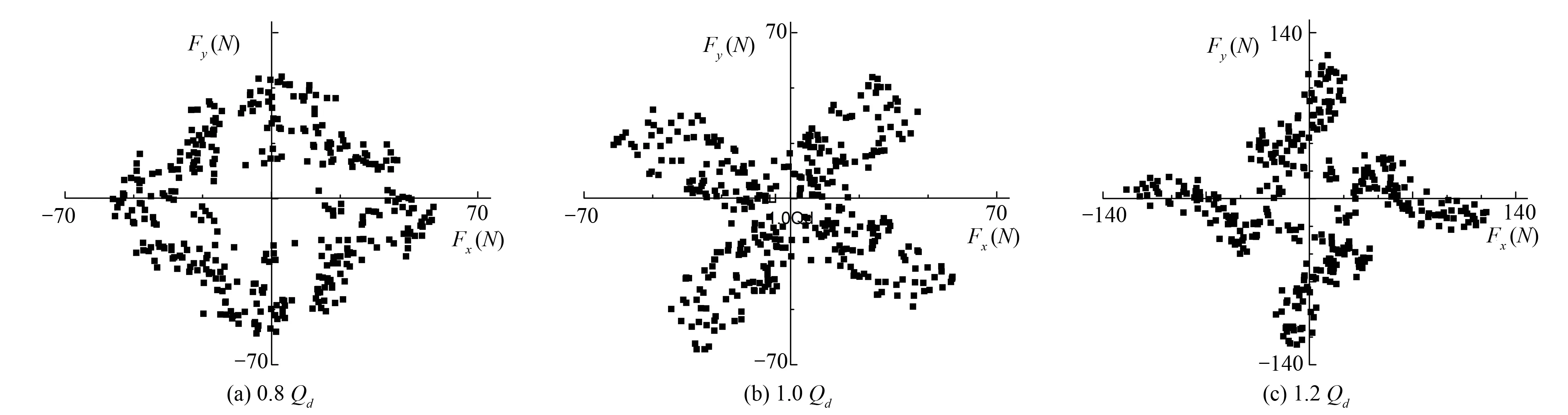
圖10 葉輪徑向力矢量圖Fig.10 Vector diagram of impeller radial force

(2)葉輪的軸向力。圖11給出了葉輪在旋轉一圈過程中不同工況下軸向力的時域圖。可以看出，不同工況下葉輪軸向力也出現28個波峰波谷，與徑向力一樣，葉輪、導葉的動靜干涉對葉輪軸向力也有較大影響。相比較徑向力的波動而言，葉輪軸向力波動振幅較小，比較穩定。隨著流量的增加，葉輪的軸向力逐漸增加，軸向力平均值分別為900 N，915 N，931 N，分別大于徑向力；同時可以看出相鄰工況下的軸向力差值幾乎相等。

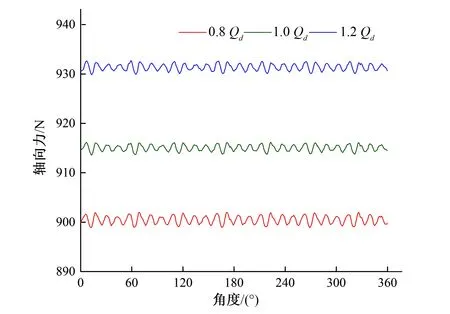
圖11 葉輪軸向力時域圖Fig.11 Time domain diagram of impeller axial force

3.3 壓力脈動分析

泵內的壓力脈動情況對于泵的運行穩定性、可靠性有很大的影響，有必要對其進行分析。本文對潛水泵的主要部件葉輪和導葉上設置壓力脈動的監測點，通過數值計算得到其非定常特性。由于葉輪和導葉流道具有對稱性，選取單個流道內的相應位置設置監測點。監測點的設置如圖12所示，其中在葉輪中間截面上的葉片工作面和背面各設置了4個監測點，葉輪流道的中間流線上設置4個監測點，彼此均勻分布；在正導葉流道、過渡段流道位于中間截面上分別設置2個監測點與1個監測點；在反導葉流道的中間截面上設置3個監測點。

圖12 壓力脈動監測點Fig.12 Monitoring points of pressure fluctuation

模擬計算的結果得到的壓力值為各個監測點在不同時刻的靜壓值，為了更加形象比較壓力大小，引入壓力系數Cp：

(3)

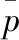
圖13是0.8Qd工況下各監測點的壓力脈動時域圖。可以看到，各監測點處的壓力脈動呈現明顯的周期性。葉輪葉片工作面和背面處的各點處的壓力脈動曲線出現7個主峰，葉輪流道中間流線處的壓力脈動除了葉輪出口外，其余主峰數也為7，與導葉葉片數7對應，可見導葉對于葉輪內部流道的壓力脈動的干涉較大。葉輪流道中間出口處至正導葉中間流道處的脈動曲線出現4個主峰，從過渡段處至反導葉流道主峰數變至28個，可以看出對于葉輪出口處及正導葉內部流場，葉輪對其脈動較大；對于正導葉出口至反導葉出口的內部流道，脈動比較復雜，主要體現出葉輪及導葉在此產生的干涉作用。

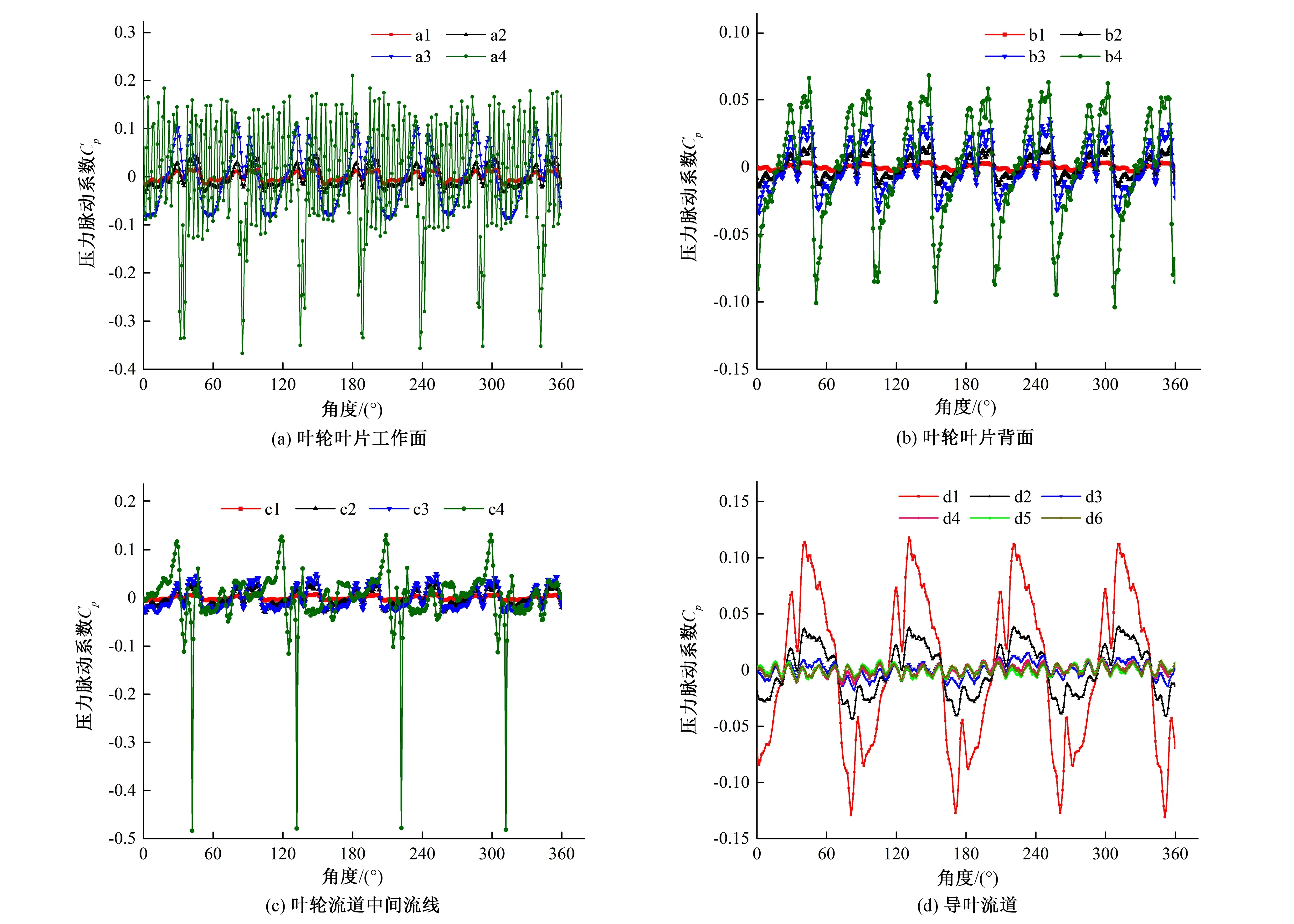
圖13 0.8Qd各監測點的壓力脈動時域圖Fig.13 Time domain diagram of pressure fluctuation at 0.8Qd

由圖13也可以看出a4處波動異常劇烈，這是由于葉片工作面直接對工作介質做功，從前文的分析可知介質進入導葉后壓力降低，故在出口處涉及能量轉化，情況比較復雜；同時參考圖7(a)可以看到該處處于幾個不同等級的壓力區的匯集處，所以壓力波動比較大。但是如上文所述葉輪在轉過不同流道的時間內也是呈現出來一定的周期性。對于葉輪葉片的工作面、背面以及中間流線，從葉輪進口至出口壓力脈動幅值都是由大到小變化；對于葉輪的單個流道的壓力脈動，從葉輪葉片的工作面至背面，其幅值沿周向逐漸減小。正導葉內的壓力脈動幅值沿徑向逐漸減小，至過渡段及反導葉段脈動穩定，并且特征趨于一致。

圖14與圖15分別是設計工況與1.2Qd工況下的壓力脈動時域圖。可以看出兩種工況下各點的壓力脈動的波動趨勢與設計工況保持一致，各點處進入高壓區與進入低壓區的時刻點相同。下面選取1.0Qd工況，也就是設計工況，來作為典型樣本進一步分析。

基于快速傅里葉變換(Fast Fourier Transform)將時域數據變換得到頻域數據，從而進行頻譜分析，如圖16所示。其中定義軸頻倍數NF：

NF=60F/n=F/Fn

(4)

式中：F為傅里葉變換后的頻率；Fn為相應轉速下泵軸的轉動頻率(APF)，本文Fn=24.17 Hz。

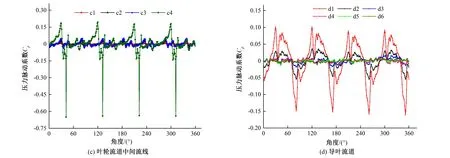
圖14 1.0Qd各監測點的壓力脈動時域圖Fig.14 Time domain diagram of pressure fluctuation at 1.0Qd

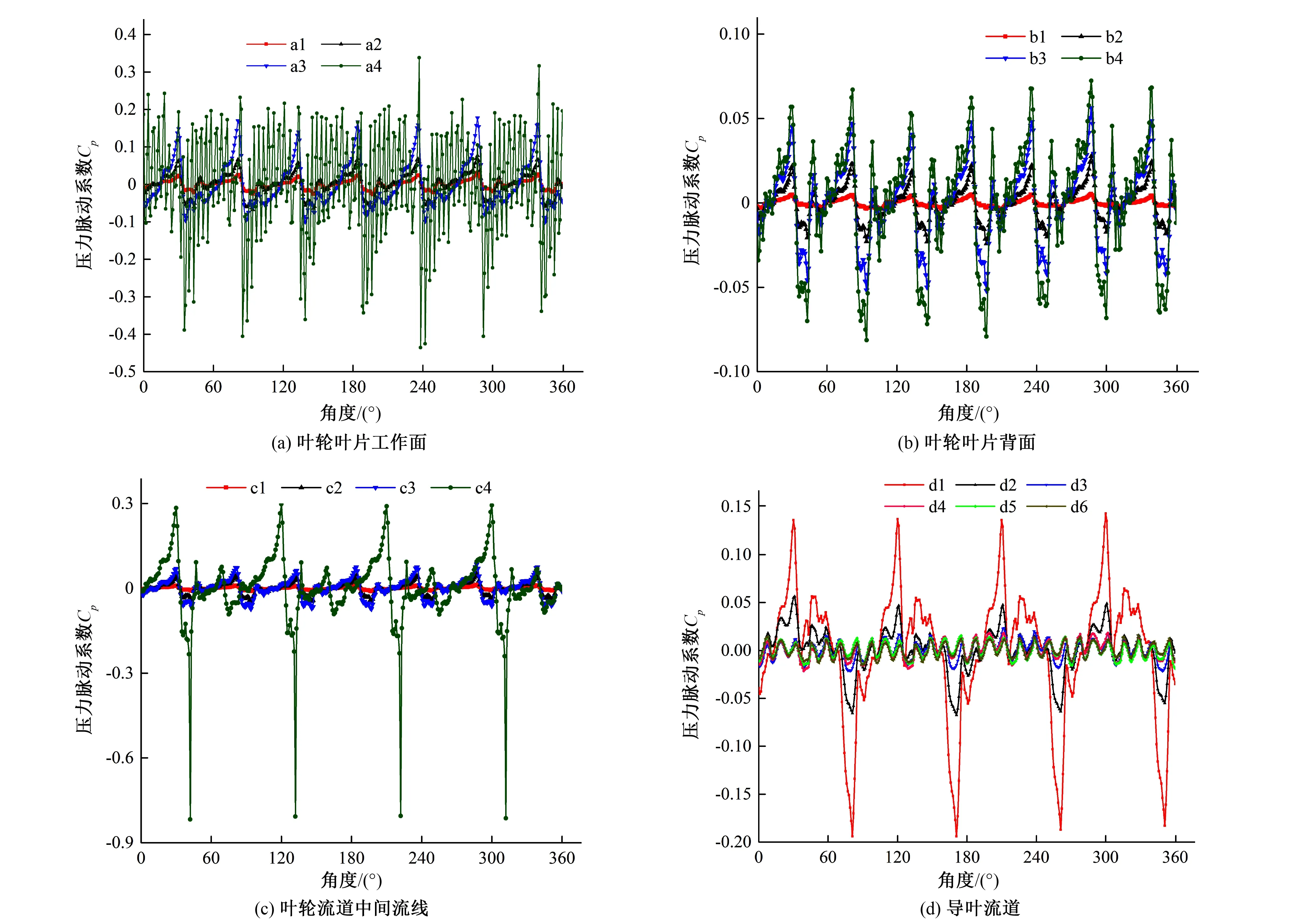
圖15 1.2Qd各監測點的壓力脈動時域圖Fig.15 Time domain diagram of pressure fluctuation at 1.2Qd

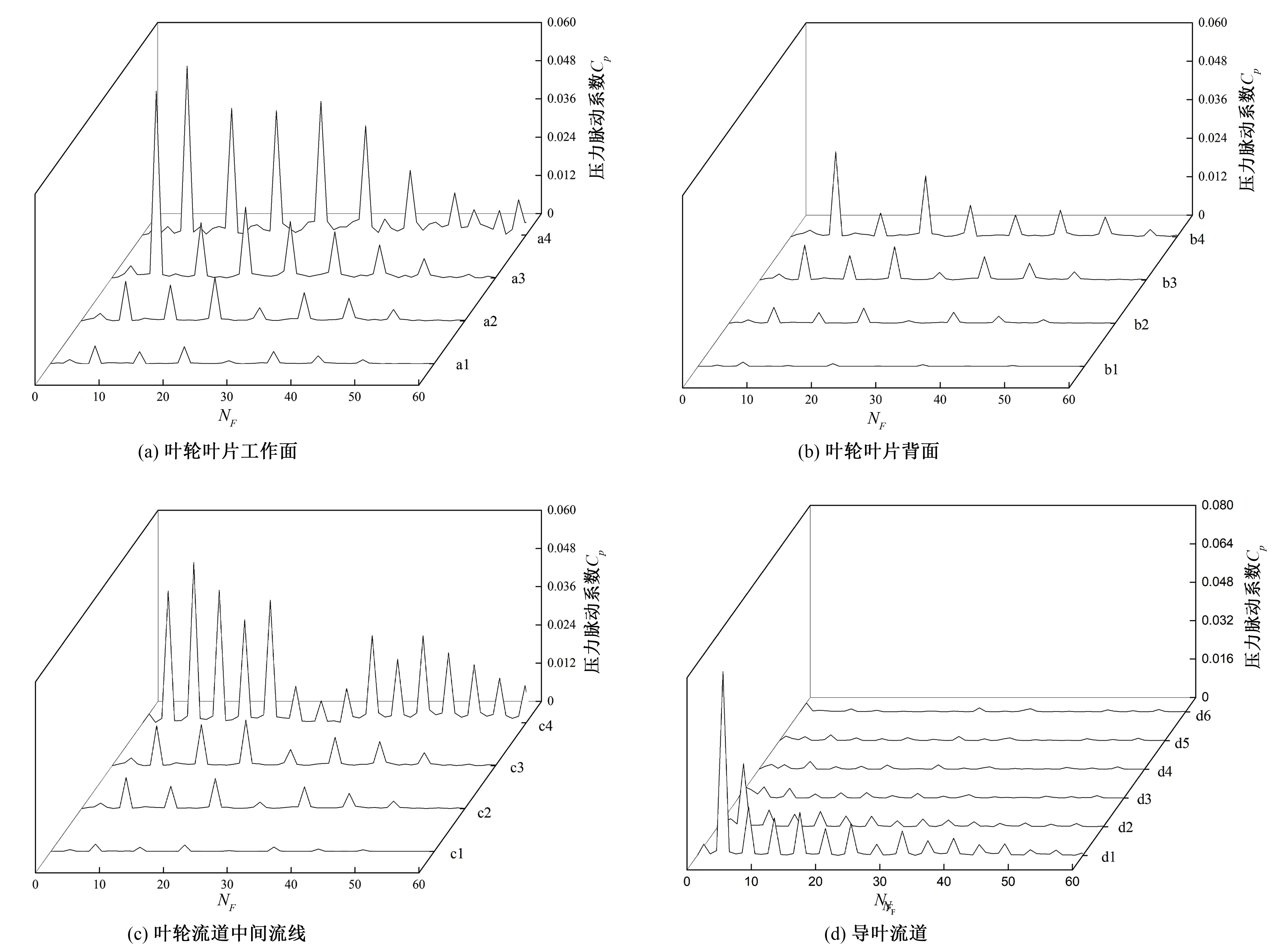
圖16 1.0Qd各監測點的壓力脈動頻域圖Fig.16 Frequency domain diagram of pressure fluctuation at 1.0Qd

由圖16可見，葉輪中無論葉片的工作面、背面還是中間流線，壓力脈動Cp幅值都是在NF為7的時候達到最大值，也就是說葉輪的壓力脈動的主頻為軸頻的7倍，即為7APF(169.17 Hz)。同時也可以發現，葉輪內除了中間流線出口處的監測點外，其余監測點的次頻都是7APF的倍數。導葉內的主頻由正導葉內的4APF逐漸變化到過渡段與反導葉內的7APF。4APF對應葉輪葉片數，7APF對應導葉葉片數，由此可見葉輪和導葉內的壓力脈動主要是葉輪與導葉的動靜干涉作用導致。

4 結 語

(1)在設計流量下，揚程與效率的計算值為20.15 m、75.42%，與試驗值的偏差分別為2.6%、1%，流量不大于1.2Qd時數值計算較為準確；在流量大于1.2Qd工況下，潛水泵發生汽蝕，導致計算偏差較大。

(2)不同流量下，導葉內的過渡段總存在大小不一的漩渦，損失較大；其中設計工況下的液流漩渦規模最小，相對最穩定。

(3)葉輪的徑向力與軸向力受葉輪與導葉的動靜干涉影響，在旋轉一圈的時間內均出現28個波峰波谷。其中軸向力的波動振幅小于徑向力，但是其平均值大于徑向力。

(4)葉輪的壓力脈動受葉輪與導葉的干涉，其主頻為軸頻的7倍(7APF)，導葉內的壓力脈動的主頻由正導葉內的4APF逐漸變化到過渡段與反導葉內的7APF。

□