海上浮式風機時域耦合程序原理及其驗證

陳嘉豪, 劉格梁, 胡志強

(1. 上海交通大學 海洋工程國家重點實驗室; 高新船舶與深海開發裝備協同創新中心，上海 200240; 2. 紐卡斯爾大學 工程學院, 紐卡斯爾 NE1 7RU，英國;3. 中國能源建設集團廣東省電力設計研究院有限公司，廣州 510663)

近十年來，由于各國日漸重視可再生能源的轉型發展，海上風電技術及其相關產業在全球呈現蓬勃發展的態勢[1].而隨著近海優質風電資源的日益開發，海上風電產業也如同過去油氣產業所經歷的變革一樣，逐漸從陸地走向海洋，從淺海過渡到中等或更深的水域，其相應的支撐平臺形式也從固定式逐漸過渡為浮式[2].但由于海上浮式風機具有復雜的多物理場耦合特性，如何準確、快速地對海上浮式風機的耦合動力特性進行數值預報，成為一直以來的研究難點與熱點問題之一[3].

目前，海上浮式風機的數值分析主要分為頻域計算和時域計算.早期研究人員主要借鑒離岸油氣工業的經驗，利用頻域分析法對海上浮式風機進行設計與分析[4-5].雖然，頻域分析法能夠快速簡便地計算海上結構物的頻域動力響應特性，但由于海上浮式風機涉及空氣動力學、水動力學、結構動力學、錨泊動力學及控制系統等技術，其動力響應具有高度的非線性特性.頻域分析法無法全面、準確地分析海上浮式風機的耦合動力響應特性.在這之后，國際上一些研究人員改寫或調用固定式風機或機械行業的計算軟件，用以時域計算并分析海上浮式風機的耦合動力特性，如FAST[6]、 HAWC2[7]、 Bladed[8]、 Adams、 Simpack等軟件.在國內，唐友剛等[9]利用水動力計算軟件(HydroD)對自主設計的新型海上浮式風機在頻域范圍內進行動力學仿真.Ma等[10]利用FAST軟件對立柱型浮式平臺耦合動力響應進行時域計算分析.趙文超等[11]利用計算流體動力學(CFD)滑移網格技術對海上浮式風機的氣動性能做了仿真計算.劉利琴等[12]針對垂直軸的海上浮式風機開發了氣動-水動力耦合數值仿真程序.當前，國內外關于海上浮式風機的全耦合時域仿真程序尚在研究中，且國內對于海上浮式風機相關理論的研究及數值程序的開發與國外同行尚有一定差距.

本文介紹自主研發的用于海上浮式風機的氣動-水動-結構-錨鏈-控制全耦合時域數值仿真程序(DARwind)的相關理論方法.在氣動計算方面，利用非定常葉素-動量理論計算風機的氣動載荷；在水動力計算方面，利用Airy線性波浪理論、勢流理論以及Morison方程計算相關的水動力載荷；在錨泊模型方面，采用準靜態的懸鏈線錨泊模型計算錨鏈張力；在多體動力學方面，利用Kane動力學方程構建系統的動力學方程，并求解各自由度的加速度信息；在柔性動力學方面，對于如塔架和槳葉等柔性體，采用高階變形模型以考慮非線性的剛柔耦合效應；對比測試DARwind程序與FAST軟件，以驗證DARwind程序在海上浮式風機數值仿真方面的有效性.本文可為海上浮式風機耦合動力理論及其相關的數值仿真程序的研發提供一定的參考依據.

1 理論模型

1.1 水動力模型

DARwind程序中，利用Airy線性波浪理論、勢流理論以及Morison方程計算相關水動力載荷[13].部分水動力參數，如：復原力系數、波浪激勵力傳遞函數、波浪輻射力傳遞函數、二階波浪力的二次傳遞函數(QTF)矩陣均由三維頻域勢流軟件，如WAMIT、Sesam等，進行頻域計算并生成.這些頻域水動力參數將作為DARwind程序的讀入數據，再依據實際計算的波幅信息、平臺的位移、速度和加速度等參數，實時生成時域水動力載荷.其中，黏性阻力采用Morison經驗公式進行修正.

波浪激勵力FW包含波浪入射力和繞射力，考慮線性化的一階波浪力，并采用諧波疊加法進行計算，即

(1)

式中：上標W為波浪激勵；fn為第n個單元規則波的頻率；εn為第n個單元規則波的相位；An為第n個單元規則波的波幅；HW(ifn)表示頻率為fn的波浪力的頻率響應函數；t為時間.

考慮自由表面記憶效應，波浪輻射力采用間接時域計算方法，利用頻域勢流理論計算可以獲得輻射水動力參數μjk、λjk，再經過下面的公式，可以得到時域輻射力

(2)

j=1,2,…,6

(3)

沿濕表面對平臺在水中受到的靜壓力積分可以獲得浮體的靜水力載荷，分為平臺正浮時的浮力和平臺發生位移時的靜水回復力，其中靜水回復力的表達式為

(4)

對于平臺的細長構件，由流體黏性引起的載荷較為明顯，勢流理論無法準確地計算該載荷.此時，可根據Morison經驗公式對勢流載荷進行黏性修正.圓柱體在lx處離散的切片長度為dl的流體黏性力FV表達式為

(5)

式中：上標V為黏性；CD為黏性系數，一般由實驗測得；D為圓柱直徑；dl為圓柱離散的切片厚度；νw為水質點在切片處垂直于切片軸向的速度分量，其值等于波浪運動導致的水質點的速度與海流引起的速度在該方向的速度分量之和；νs為切片的運動速度在垂直于切片軸向的速度分量.黏性力矩陣包含集中力和力矩，沿著圓柱總長度LC進行積分，表達式為

(6)

因此，總的水動力FH根據線性理論，為上述FW、FR、FS和FV之和，則有

FH=FW+FR+FS+FV

(7)

1.2 錨泊動力模型

錨泊系統對海上浮式風機平臺起到基本的定位和約束作用，同時影響著浮式結構物的運動響應特性.DARwind程序采用準靜態的懸鏈線錨泊模型[14]計算錨泊對平臺的約束載荷.其中，除錨泊的伸長變形外的一些動態特性，如慣性力、阻尼力、錨鏈變形彎矩均被忽略不計.

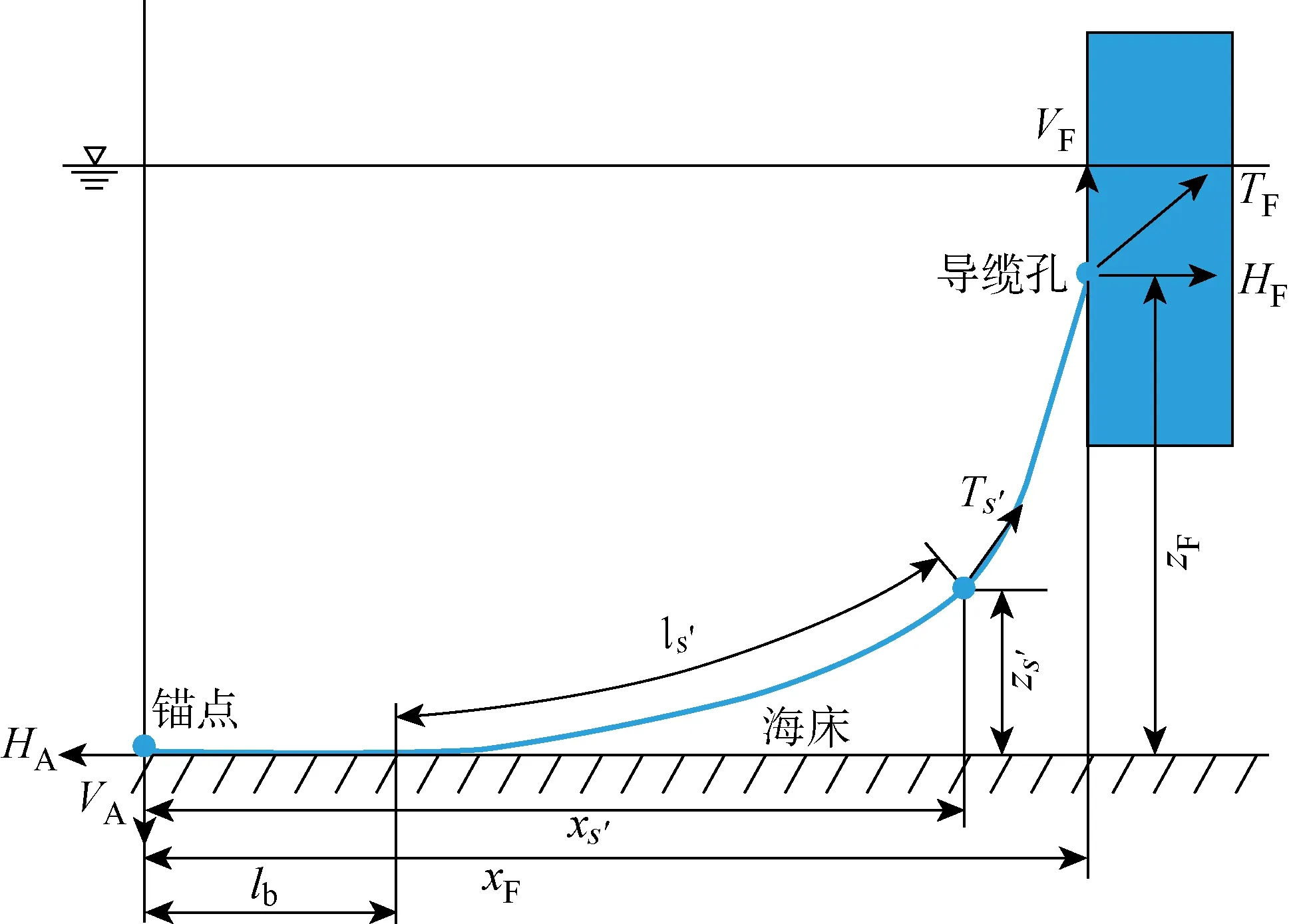
圖1 懸鏈線錨泊示意圖Fig.1 The schematic diagram of catenary mooring lines

懸鏈線錨泊模型如圖1所示.其中，錨點受到水平方向張力HA和垂直方向張力VA的作用.假定躺底段(錨鏈與海床接觸的部分)長為lb；錨鏈任意一點的張力為Ts′，水平方向的張力為Hs′，垂直方向的張力為Vs′，其距離錨點的水平距離為xs′，垂直距離為zs′，從躺底點算起的錨鏈自然長度為ls′；導纜孔的張力為TF，該張力水平方向的分力為HF，垂直方向的分力為VF；導纜孔到海底的垂直距離為zF，錨鏈整體的水平投影長度(水平距離)為xF；錨鏈的總長度為L，濕密度為w, 截面面積為A，軸向剛度為EA.

當錨鏈與海底接觸時，即lb≠0，錨點處此時沒有垂向張力作用于錨鏈.根據導纜孔和錨點之間的水平距離和垂向距離，平臺導纜孔處對錨鏈的水平張力和垂向張力有如下關系式：

(8)

(9)

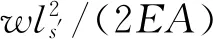
當lb=0時，錨點對錨鏈的垂向張力等于導纜孔對錨鏈的垂向張力減去錨泊質量，關系式為

VA=VF-wL

(10)

此時，導纜孔處的水平張力和垂向張力的關系式為

(11)

(12)

只要獲得錨鏈當前時刻的錨點和導纜孔的位置(一般情況下，錨點的位置保持不變，導纜孔的位置需要根據當前的平臺位置信息獲得)，通過上述非線性方程組即可求得導纜孔對平臺的約束張力.其中，非線性方程的數值求解可以借助迭代技術，如牛頓迭代法等進行數值求解.

1.3 空氣動力模型

葉素-動量法[15]結合了一維的動量理論和二維的葉素理論.動量理論是基于理想的無窮槳葉正對來流時的致動盤假定推導而獲得的.葉素理論則考慮了槳葉的實際形狀，將槳葉劃分為許多二維的翼型剖面，稱之為“葉素”.根據每一個葉素上實際入流風速計算獲得局部入流攻角，然后根據入流攻角從翼型氣動系數的數據庫中插值獲得當前翼型剖面的氣動系數，如升力系數、阻力系數和轉矩系數等.根據這些系數，結合相對入流風速即可計算獲得該剖面的氣動載荷.最后，再通過積分(疊加)各個槳葉剖面葉素的氣動載荷，計算總的風機氣動載荷.令由動量理論得到的氣動載荷和由葉素理論得到的氣動載荷在環形控制體(見圖2(a))內保持相等，即可得到各不同徑長的環形控制體內的槳葉葉素的誘導系數，其表達式為

(13)

(14)

式中：a為軸向誘導系數；a′為切向誘導系數；σ=crbBblade/(2πrb)為風輪實度，其中Bblade為槳葉數，rb為葉素的徑向長度，crb為葉素局部弦長；φ為入流角；CL和CD分別是葉素升力和阻力系數.

圖2 氣動模型示意圖Fig.2 The schematic diagram of aerodynamic model

在經典的葉素動量理論中，假定葉輪只有轉動，且來流是空間均勻和時間定常的.但對于實際的海上浮式風機而言，空氣流動是時空變化的，浮式平臺的運動也會引起槳葉的運動，加劇其相對入流風速的變化，氣動誘導系數也隨時空所變化，因此必須考慮非定常的局部氣動模型，如圖2所示.其中，α為葉素的局部入流攻角.為了簡化模型，各葉素的氣動性能只考慮小范圍控制體內的影響.其研究的單元氣動影響區域為一個扇形區域，如圖2(c)所示.該扇形區域面積是圖2(a)所示的環形控制體區域面積的1/3，即在當前時刻每個槳葉的葉素氣動計算只考慮該槳葉附近區域的影響.

當不考慮槳葉柔性變形和平臺運動所帶來的葉素運動，葉素的相對入流風速如圖2(b) 所示，其表達式為

(15)

式中：v0為上游未受干擾的入流風速大小；Ω為風輪的轉度；vrel為最終合成的相對入流風速矢量；在非定常的局部葉素-動量模型中，DARwind程序考慮了局部槳葉的葉素因平臺運動、塔架變形等引起的運動速度，以及由槳葉本身變形導致的葉素運動速度.葉素-動量法雖然計算速度快，且過去一直作為風能領域常用的可靠計算方法，但由于其并不能完全描述風場及風機的細節信息，且計算精度在特定場合可能有一定的誤差，故需要引入一些修正方法[16]，例如：通常情況下，風機槳盤面并不正對來流風，此時稱之為“偏航”狀態.對于海上浮式風機而言，由于浮式平臺的大幅度運動，這種偏航狀態更為常見，故需要考慮偏航狀態下的氣動修正；另外，由于動量理論假定葉片數量為無窮多，但實際的風輪葉片數量是有限的，風機尾流渦系與無窮槳葉的理想風輪的尾流場有差別，此時需要采用Prandtl葉尖損失模型進行修正；當軸向誘導因子約大于0.4時，簡單的動量理論不再適用，此時需要使用 Glarert 經驗公式[16-17]進行適當的修正，以使數值計算結果與實際結果更為符合.上述所提及的修正理論均被采用并編入DARwind程序的氣動模型中，程序中的葉素-動量法是一個反復迭代求解誘導系數直至收斂的過程，其計算速度關系到程序整體的仿真速度，所以此模塊還需要采用一些算法的優化技術以提高迭代計算的收斂速度.

1.4 動力學模型

海上浮式風機的多個不同部件擁有不同的特性，可各自根據相對變形量簡化為剛性體或柔性體，因此海上浮式風機模型為一個剛柔耦合的多體系統.采用浮動坐標系[18]描述剛柔耦合多體系統的運動關系.該方法采用兩套坐標系描述每個部件的位置、方向及變形：① 全局坐標系，用以描述各部件的位置和方向；② 各部件的隨體坐標系，用以描述部件的柔性變形場.其中對于柔性體，如塔架和槳葉，其變形場采用模態疊加法進行有限模態的近似離散，變形量U如下所示：

U=ΘQ

(16)

式中：Θ為模態形狀函數矩陣；Q為模態坐標(廣義坐標)矩陣.研究表明[19-20]：當柔性體進行大范圍運動時，尤其是高速旋轉運動，用傳統的線性化方法將會產生較大的數值誤差.因此在DARwind程序中，柔性體(塔架和槳葉)均被近似為三維的Euler-Bernoulli 模型.當發生大范圍的運動時，梁的側向變形會導致軸向的耦合收縮效應，并且隨著運動頻率的增加，柔性體的剛度將會隨之增加，該效應稱為剛柔混合多體的“動力剛化”.三維梁模型的高階非線性耦合變形量可簡化為

(17)

式中：ush是由梁結構側向變形引起的軸向收縮量；uy0和uz0分別是梁側向變形量關于局部隨體坐標系y，z方向的分量.當考慮高階非線性耦合變形效應時，上述的柔性變形可以表示為

(18)

其中非線性高階耦合效應矩陣H為

(19)

(20)

式中：下標x為對應物理量的坐標分量.通過上述的浮動坐標系法及模態離散，可以描述系統各部件的各個質點之間的運動學模型.研究中需要構建系統的動力學控制方程，以求解系統在外力和系統約束作用下各自由度的信息.采用Kane動力學方程[21]構建系統動力學控制方程.這種方法兼具矢量力學和分析力學特點，既避免了出現理想約束反力，也避免了對動力學函數進行求導，減少了計算工作量，且易于拓展和推廣.

一個質點系統，關于第j個廣義速度的Kane方程可表示為

Fj+F*j=0

(21)

廣義主動力Fj以及廣義慣性力F*j分別計算如下：

(24)

(25)

式中：Bki和Dki分別為部件i的平動和轉動的加速度余項，其解析表達式較為復雜，可通過線速度和角速度關于時間的一階導數推導而得，需要注意各個部件的坐標系之間的轉換關系.

對于剛柔伺服多體耦合的海上浮式風機系統，其Kane方程可表示為

(28)

Nr+Nf+Ns=N

將式(28)中的各部件的廣義主動力和慣性力分別進行累計計算，則有

(29)

(30)

式中：Fi和Mi分別為部件i的動力學參考點的力和力矩；mi和Ii分別為部件i的質量和轉動慣量；式(29)右端第一項為剛體和柔性體的廣義主動力，比起剛體，柔性體中存在額外的結構變形能Ei；式(29)右端的第二項為控制器的廣義主動力或內力；式(30)右端為剛體和柔性體的廣義慣性力和力矩.在海上浮式風機系統中，浮式支撐平臺、機艙、轉軸和輪轂結構均視為剛體，塔架和槳葉均視為柔性體.需將柔性體劃分為許多微小單元，對每個微單元分別建立Kane方程，故柔性體的存在增加了動力學方程的復雜度和計算量.

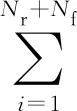
[IiDi+ωi×(Iiωi)]}=0

(31)

令

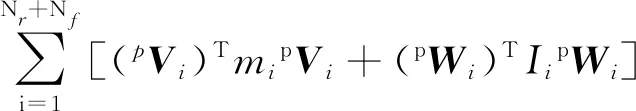
(32)

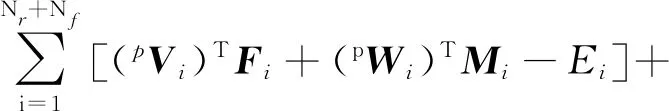
[IiDi+ωi×(Iiωi)]}

(33)

(34)

1.5 控制系統模型

DARwind程序采用發電機轉矩控制器和槳距角控制器.當風速小于額定風速時，以優化風能捕獲效率為目標，通過調節發電機轉矩進而調節風機的最佳葉尖速比；當風速達到或超過額定風速后，則主要通過改變槳距角控制系統調節氣動性能，進而達到穩定功率的目的.

圖3 發電機轉矩控制Fig.3 Generator-torque control

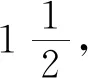
槳距角控制器采用比例-積分統一變槳機制，其表達式為

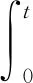
(35)

式中：θ為槳距角；Δθ為當前需要改變的槳距角度；t為槳距角控制器的執行時間；ΔΩ為當前風輪轉速與目標轉速之差；KP=KPc/[1+(θ/θc)]為槳距角控制器的比例項，其中θc為當槳距角為此值時，功率對槳距角的導數為槳距角等于0時所對應的導數的2倍，KPc為θc槳距角下的比例項；KI=KIc/ [1+(θ/θc)]為槳距角控制器的積分項，KIc為θc槳距角下的積分項.二者的具體取值需要根據實時的槳距角動態進行調整，其推導過程可參考文獻[22].

1.6 程序計算流程

運用上述理論模型構建用于海上浮式風機動力性能預報的DARwind程序，計算流程如下：

(1) 程序開始時，讀入標記參數、結構信息及環境信息等，用以初始化計算模型.

(2) 在每一個計算時間步下，程序需要根據平臺的位置、速度信息及平臺參考點處的波浪場信息生成相應的水動力載荷；根據槳葉的變形、運動及局部槳葉在當前時空的風場風速，利用非穩態葉素-動量法計算氣動載荷；根據平臺的位置信息計算導纜孔的位置；利用懸鏈線錨泊模型計算當前錨鏈對平臺的約束力.另外，程序還考慮了重力、浮力及控制器的作用力等參數.

(3) 經過步驟(2)求得所有環境載荷后，通過Kane方程構建系統動力學控制方程，求得當前各自由度的加速度信息，并利用4階Runge-Kutta時間積分法遞推下一時刻各自由度的位置及速度信息.

(4) 程序依次循環直到預設的結束時間.

相比于其他類似程序，DARwind程序有兩方面的創新[23]：一方面，該程序可以非常簡便地根據不同計算目的，對海上浮式風機系統建立不同的多體系統方案.例如：當需要快速獲得海上浮式風機系統的動力特性時，可將整個系統作為單體模型；當需要適中的計算速度和精度時，可以將整個系統作為多剛體結構，忽略柔性結構的影響；當需要較為準確的系統模型時，可將海上浮式風機系統作為剛柔耦合多體模型.另一方面，DARwind程序中創新地采用了高階的剛柔耦合模型，考慮了剛體運動對柔性體動力性能的影響.

2 對比驗證

DARwind程序將與美國國家可再生能源實驗室(NREL)的風機仿真FAST 程序[6]進行對比分析，以驗證DARwind程序在海上浮式風機數值仿真方面的有效性.采用OC3-Hywind Spar海上浮式風機作為研究對象，如圖4所示，關于該海上浮式風機更詳細的信息可以參考文獻[24].

圖4 OC3-Hywind Spar海上浮式風機[24]Fig.4 OC3-Hywind Spar floating offshore wind turbine[24]

2.1 固有頻率測試

在相同的模型參數設置下，DARwind和FAST程序在自由衰減運動中測得的固有頻率以及無因次阻尼系數如表1所示.由表1可知, 除了縱搖運動具有微小的差異之外，DARwind以及FAST程序的自由衰減運動的特性都是非常接近的.該結果表明DARwind程序能準確地反映海上浮式風機系統的質量、慣性、靜水回復力、錨鏈剛度及水動力阻尼等特性.

表1 DARwind和FAST程序中的運動固有頻率與無因次阻尼系數

Tab.1 Natural frequency and damping coefficient of platform motions in DARwind and FAST softwares

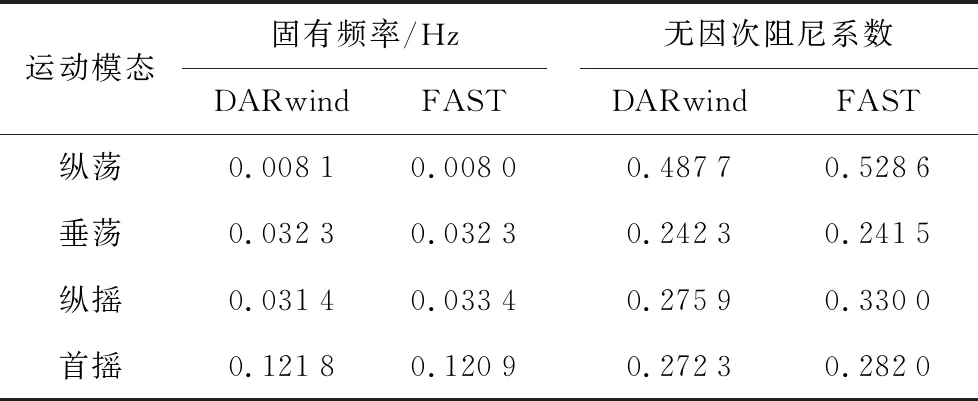
運動模態固有頻率/HzDARwindFAST無因次阻尼系數DARwindFAST縱蕩0.00810.00800.48770.5286垂蕩0.03230.03230.24230.2415縱搖0.03140.03340.27590.3300首搖0.12180.12090.27230.2820

2.2 風工況

海上浮式風機是用以捕獲風能的離岸設備，對其氣動性能及結構變形的預測對海上浮式風機而言同樣也是需要重點考慮的因素.對DARwind程序進行穩態風工況測試，測試結果如表2所示.數值計算中，風速空間均勻且時間定常；轉速為風輪轉速；槳距角設置為0°.當不考慮控制系統的作用且平臺固定時，該工況的測試結果如表3所示.由表3可知，DARwind 程序的氣動載荷值(氣動推力和氣動轉矩)比FAST程序的氣動載荷值略大，這可能是由于兩個數值軟件在氣動理論方法上的差異所導致的.DARwind程序采用的是基于葉素扇形影響區域的局部非穩態氣動模型；而FAST程序則采用的是基于風輪整體的穩態氣動模型.在塔架和槳葉的變形方面，相比于FAST程序，DARwind程序的計算結果相對較小，但兩者差別不大.這主要是由于DARwind程序采用了高階的剛柔耦合模型(見式(17)～(20))，考慮了剛體運動對柔性體的影響.當柔性體發生大范圍運動(如高速轉動)時，柔性體的剛度會隨之提高，變形也會隨之減小.總體而言，無論是氣動性能還是結構彈性動力特性，兩個程序的計算結果都比較接近，這驗證了上述柔性體變形理論及葉素-動量理論在海上漂浮式風機時域計算的有效性.

表2 穩態風工況測試Tab.2 Steady wind cases

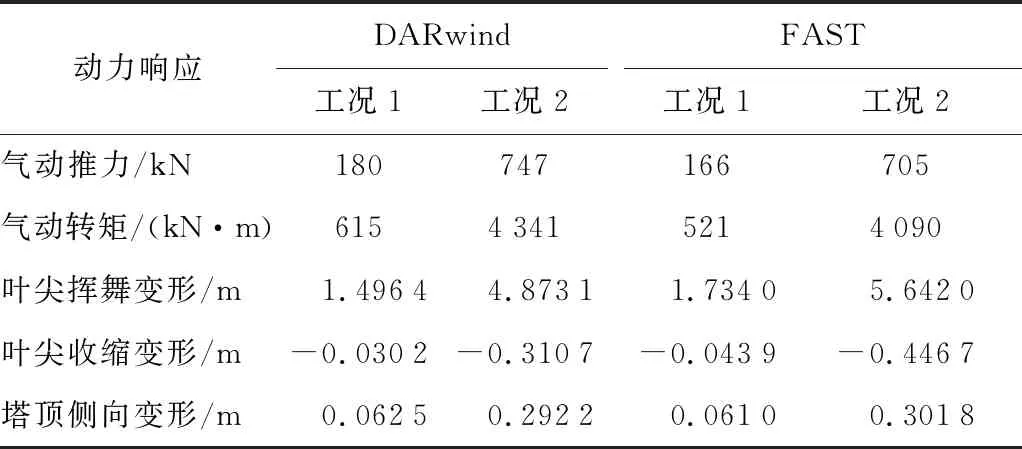
表3 氣動載荷與葉尖變形量Tab.3 Aerodynamic loads and blade-tip deflection

2.3 風波聯合工況

海上浮式風機工作于有風及波浪載荷共同作用的海洋環境下，因此，對浮式平臺運動特性的預報顯得尤為重要.下文將驗證DARwind程序在風波聯合工況下的運動特性.測試風速為額定風速(11.4 m/s)；風輪保持額定轉速(12.1 r/min)；槳距角統一設置為0°；不考慮控制器的作用；波浪模型參考“北海聯合海浪計劃”(Jonswap)波浪譜，有義波高Hs為2.0 m；譜峰周期Tp為8.0 s；譜形參數r設置為3.3.DARwind 和 FAST 程序的縱蕩及縱搖的功率譜密度對比如圖5所示.由圖5可知，兩種數值程序在風波聯合工況下的運動特性吻合得較好，且均能反映出縱蕩及縱搖運動中明顯的共振響應、波浪能量區的強迫運動響應、縱蕩及縱搖的耦合運動效應.

圖5 平臺運動功率譜密度Fig.5 Power spectral density of platform motion

2.4 控制系統模型

在海上浮式風機正常運轉的過程中，控制系統起著重要的作用，不但能夠調節海上浮式風機的氣動載荷與發電功率，而且對海上浮式風機的運動響應有著重要的影響.在變槳距控制過程中，通過槳葉的槳距角、風機功率等參數的變化情況，驗證 DARwind 程序控制系統的有效性.測試中，海上浮式風機的平臺受載荷運動的影響，對控制系統的要求比較高，有別于傳統的固定式風機.在該控制系統下，槳距角隨時間的變化情況如圖6(a)所示，發電機功率隨時間的變化情況如圖6(b)所示.由圖6(a)可知，上述測試過程中的槳距角隨時間的變化呈現出波動，這是由于平臺運動導致槳葉的相對入流風速急劇變化導致的.此時，為了保持發電機功率的穩定，槳距角也需要進行相應的調整.對比這兩個程序的計算結果，總體上DARwind程序的槳距角變化波動稍微大一些，但是兩者的變化情況基本相同.圖6(b)中的發電機功率也有類似的情況.其主要原因是由于在額定工況時，FAST程序的轉矩控制依然在進行調整，而DARwind程序在額定工況下選擇穩定發電機轉矩，以減少軸系疲勞損傷.此時，變槳距控制器成為了DARwind程序唯一的發電機功率調節手段，所以其槳距角的波動會相對大一些.

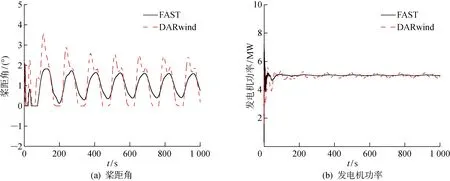
圖6 控制系統下的槳距角及發電機功率隨時間的變化情況Fig.6 Blade pitch angle and generator power vary with time

3 結語

本文介紹了海上浮式風機時域耦合仿真程序——DARwind程序的相關理論，并做了相應的數值驗證分析.研究結果表明：所采用的理論方法在海上浮式風機時域耦合計算中是有效的，DARwind程序能夠有效地仿真并準確地預報海上浮式風機復雜的時域耦合動力響應特性.然而，當前的DARwind程序仍有進一步發展和優化的空間，如：可以進一步提升氣動模型精度，尤其對于海上浮式風機大范圍搖擺運動導致的復雜尾流場而言；當前的控制系統也可以采用更為高級的控制方式，如神經網絡控制、模糊控制等現代智能化控制方式.