沉積路徑對激光增材制造結構件殘余應力的影響

張義福, 張 華, 朱政強, 蘇展展

(1. 南昌大學 機電工程學院, 南昌 330031; 2. 九江學院 機械與材料工程學院, 九江 332005)

激光金屬沉積(Laser Metal Deposition，LMD)是向熔池中注入金屬粉末制造零部件的一種快速成形工藝，已成功制造出工具鋼、高合金鋼和鎳基合金等零部件.工件受到不均勻的溫度變化時，其內部會產生殘余應力，殘余應力的累積導致沉積層變形開裂，影響LMD增材制造技術的應用.H13工具鋼是模具和工具行業的重要材料，其沉積結構主要由回火和和非回火馬氏體組成[1-2].在高冷卻速率下，工具鋼發生馬氏體轉變，成為引起殘余應力的又一原因.控制熱輸入、基材預熱、沉積層熱處理和基材與沉積層間感應加熱等技術可有效降低沉積工件殘余應力[3-4].如果殘余應力值已知，則便于選擇最優降低殘余應力的工藝參數.有限元分析是焊接過程中分析應力的數值模擬工具，可有效預測H13工具鋼在LMD制造工藝中的殘余應力.

Vasinonta等[5]建立了304不銹鋼激光沉積薄壁結構的2D熱力學模型，研究了激光功率和速度等工藝參數對熔池尺寸以及沉積壁殘余應力分布的影響.但該模型忽略了沉積壁自由面與周圍區域的對流和輻射.此外，該模型未考慮熱源在熔池區域的分布.Fu等[6]開發了三維有限元仿真模型模擬Ti6Al4V多層沉積，以理解溫度梯度機制，該模型結合了基于物理學層堆積方法和移動熱流，預測了熔池的形狀和尺寸.Cheng等[7-8]認為傳熱機制主要是通過粉末層與固化層傳導，但忽略了基材和表面輻射的熱損失[9].Luo等[10]詳細闡述了激光束熔化和電子束熔化沉積過程的數值模擬方法，分析了零件模型、工藝參數、網格方案和溫度等對模擬結果的影響，但其研究未分析氣體-金屬粉末流的影響機制.Steen等[11]使用生死單元技術建立了3D熱有限元模型，該模型以熱傳導作為唯一的傳熱模式，分析了沉積薄壁過程的熱行為，將熔池中的單元節點設置為熔化或過熱溫度以模擬熱輸入，確定了相對于零件幾何形狀的熱梯度位置，對減少零件制造中的變形和熱應力起到一定的指導作用.

因應力梯度小，對熱傳遞影響較小，如果采用熱-力全耦合分析會使熱和機械驅動力發生單向數據流，所以采用熱-力順序耦合分析方法模擬LMD過程.本文建立了H13工具鋼激光沉積過程的3D熱-力順序耦合有限元模型，采用生死單元技術模擬金屬沉積.首先進行3D瞬態熱分析，將獲得的全局溫度歷程加載到應力模型中.分析了之字形和單向沉積路徑對薄壁結構熱分布和殘余應力分布的影響.該模型考慮了材料在加工過程中的高度非線性熱物理和熱機屬性以及材料相變.

1 激光沉積過程有限元模擬

1.1 熱流本構方程建立

在熱-力耦合作用下以熱傳導為主的熱流控制能量平衡函數為

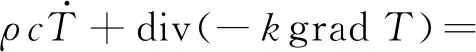
(1)

式中：ρ為密度；c為比熱容，

激光金屬沉積的溫度場源于激光束的熱輸入，其熱傳導方程由擴散熱流、對流熱流以及移動熱源組成：

(2)

粉末在4個對稱徑向相對于激光束呈30° 角以35 m/s的流速注入第1相互作用區，由于作用時間短且料流中粉末的體積分數小，所以可忽略激光與粉末的相互作用.向由基材和粉末材料組成的熔融區施加移動體熱源載荷時，新注入熔池的粉末將受到熔池熱量和激光束熱量的綜合作用.假設激光束能量的分布為均勻分布.金屬對激光(波長λ=1 064 nm)的吸收率(a)隨溫度在30%～40%內變化，則單位體積熱輸入(QV)可定義為

(3)

式中：P為激光功率.

對流和輻射的邊界條件為

(4)

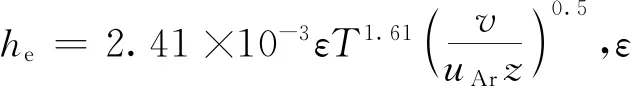
采用Fluent開發氣體/金屬粉末流CFD模型分析強制對流的熱損失參數.沉積壁周邊氣體速度分布可用于計算傳熱模型的邊界條件，如圖1所示.圖1(a)顯示了壁面上的強烈氣流區域，這些區域為強制對流區，該模型為熱傳遞模型的邊界條件計算提供了重要的數據.根據氣體速度和已經沉積壁面高度計算he(圖1(b)).沉積過程中工件溫度梯度高，材料屬性為非線性，即熱容量和熱導率為溫度的函數.相變潛熱對材料的固-固和固-液相變有很大的影響，H13工具鋼相變和等溫轉變(Time Temperature Transformation,TTT)曲線如圖2所示[12-14]，圖中：L為液相；F為鐵素體；A為奧氏體；C為碳化物；M3C為(FeCr)3C；M7C3為(FeCr)7C3；P為珠光體；B為貝氏體；M為馬氏體；MS為馬氏體轉變開始線；wc為碳的質量分數.20%，40%，80%奧氏體的等溫轉變曲線為圖中所指的3條虛線.由于激光-金屬相互作用過程中材料的溫度梯度較高，所以H13工具鋼的固-固相轉變為馬氏體相變.相變潛熱和凝固變化發生在有限溫度區間內，可通過總焓法的等效溫度分布表示，從而可獲得激光沉積過程中金屬熔化和凝固的數值解.相變潛熱效應以熱容形式等效，避免有限元分析過程中的數值不穩定性.

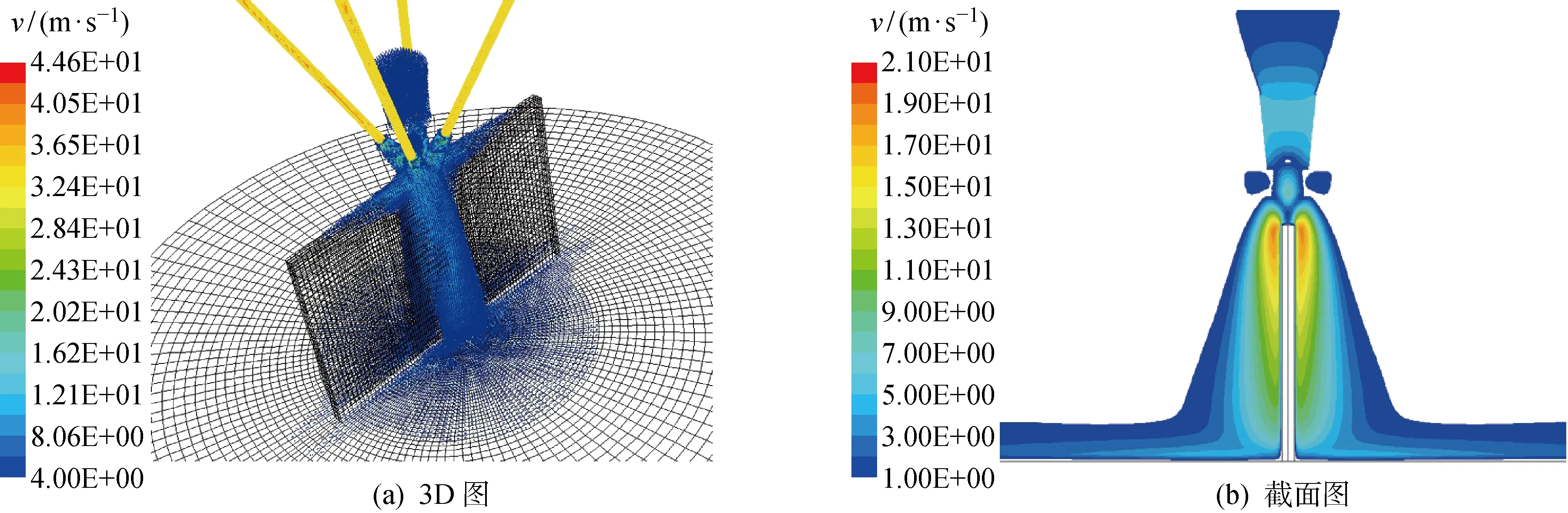
圖1 沉積壁周邊氣流速度等值線圖Fig.1 Velocity contours of gas flow around deposition wall

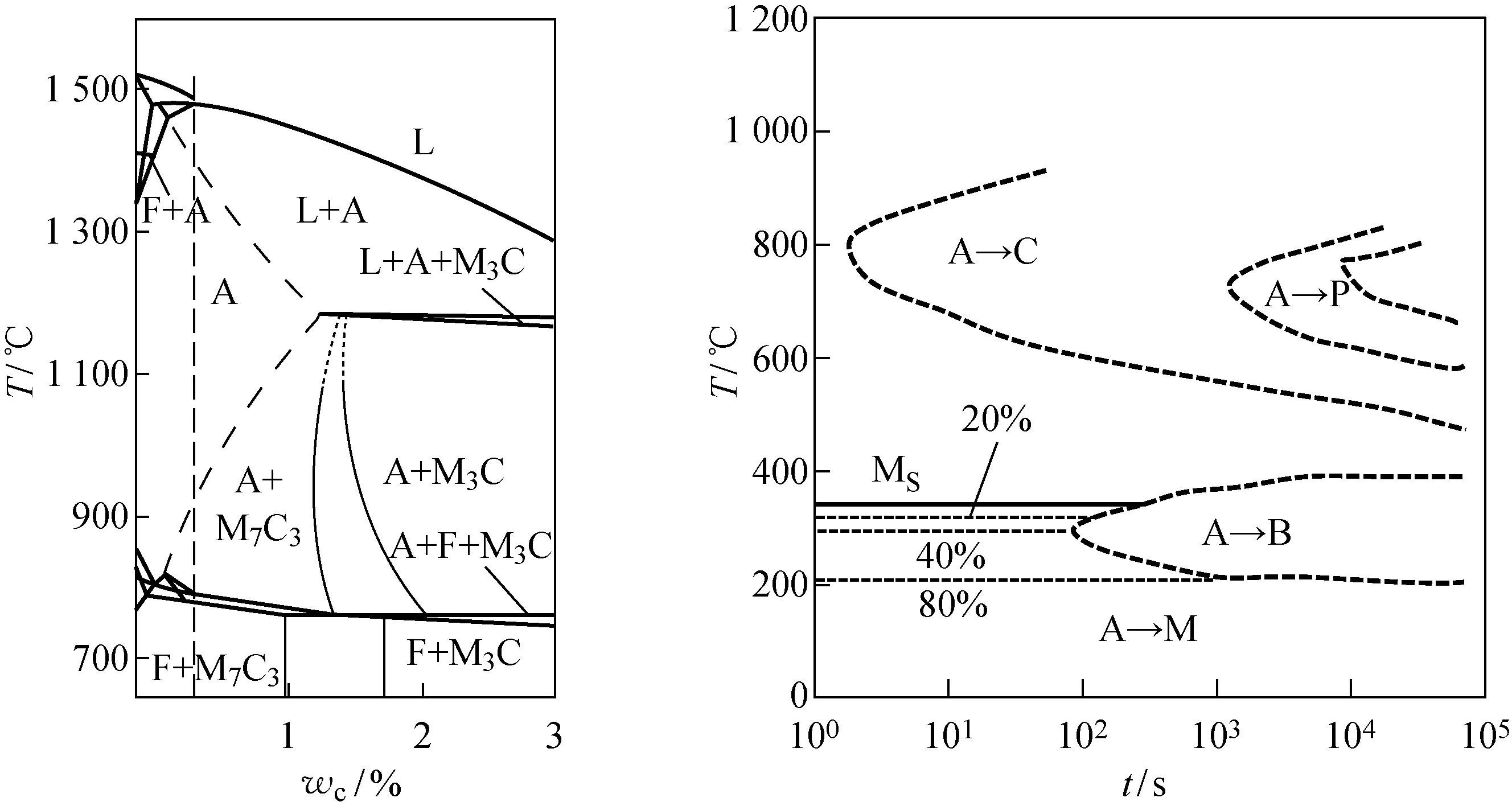
圖2 H13工具鋼相圖和TTT曲線圖[12-14]Fig.2 H13 tool steel phase diagram and TTT diagram[12-14]

1.2 熱-力順序耦合有限元模型

之字形直壁通過來回移動激光頭進行沉積制造，單向直壁每層之間的定位方向相同.H13工具鋼粉末質量流量為8 g/min，基板尺寸為40 mm×20 mm×6 mm，沉積60層，每層尺寸為30 mm×1.1 mm×0.325 mm.激光功率為200 W，焊接速度為5 mm/s，熱-力分析單元類型分別為SOLID70和SOLID45的8節點六面體網格單元，模型在笛卡爾坐標系中創建，垂直于沉積方向的水平坐標定義為x方向，沿著沉積方向的水平坐標為y方向，垂直坐標為z方向.模型單元數為 7 452，節點數為 11 028，直壁模型如圖3所示.仿真過程含2個分析步：① 采用ANSYS參數化設計語言APDL對移動熱源以及自適應邊界條件進行建模，通過熱質和熱流條件采用單元生死技術描述材料的順序沉積過程，部分已沉積外表面為對流或輻射表面，因此邊界條件采用單元生死技術.該步驟的關鍵為建立熱流本構方程.② 將沉積過程的溫度場分布歷程計算結果作為熱載荷加載至工件中，同時定義剛性基板邊界條件，以防止剛體移動，減小剛體移動對沉積件的應力影響，最終獲得殘余應力分布情況.

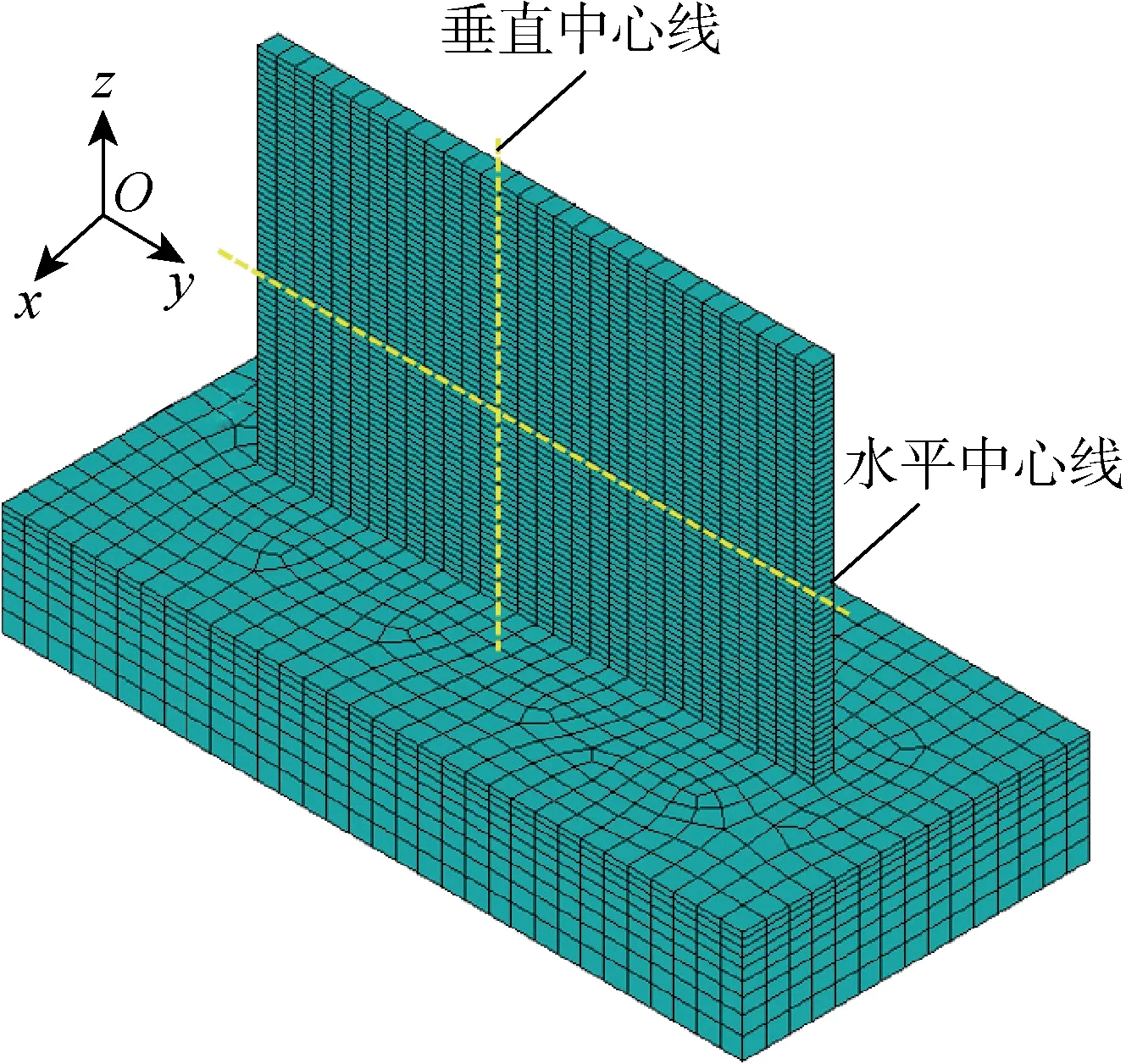
圖3 直壁網格Fig.3 Straight wall mesh

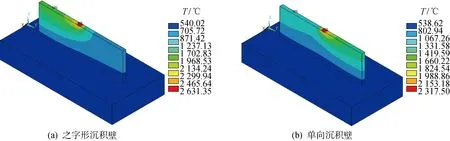
圖5 第31沉積層溫度場分布云圖Fig.5 Temperature contours of the 31st layer

H13工具鋼的熱物理性能參數和熱機性能參數參見文獻[12-15].熱容等效變化代表相變潛熱效應，屈服強度變化代表相變誘導塑性效應，熱膨脹等效變化引起相變階段體積改變.熱力學模型采用雙線性各向同性硬化模型，使用Mises屈服準則和各向同性硬化假設.沉積過程中產生的總應變(dεij)包括彈性應變(dεeij)、塑性應變(dεpij)、熱應變(dεTij)和馬氏體相變引起的變形(dεtpij)，總應變表達式為

dεij=dεeij+dεpij+dεtpij+dεTij

(5)

i,j=1,2,3

2 沉積模擬結果及分析

2.1 溫度場分布

以沉積開始作為時間起點，第31沉積層始于180 s，結束于186 s，其最高瞬態溫度隨時間的變化規律如圖4所示.圖5為第31沉積層溫度場分布云圖.可以看出，沉積熔池中的峰值溫度遠高于母材的熔點值，與類似工藝條件下的實驗結果相當[2,10]；側壁熱云圖與實驗一致[9]；沿直壁頂面以恒定功率和移動速度沉積過程中熱云圖達穩態分布；之字形沉積時，鄰近沉積壁邊緣的熔池尺寸增大并深入沉積壁，這是因為自由邊緣熱沉體積減小，此外移動反向、速度降低且每一個移動增量步均使沉積壁熱輸入量增加；單向沉積時，自由邊緣熔池尺寸增大不顯著，這是因為無激光反向即激光束從終點到起始點重新高速定位使熱輸入量在自由邊緣相對較低.

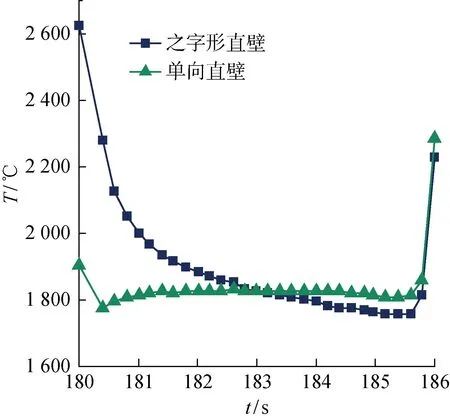
圖4 第31沉積層最高瞬態溫度曲線Fig.4 Maximum transient temperature curve of the 31st layer

2.2 應力場分析

激光沉積過程中材料受不均勻熱應力，圖6為在第31層沉積過程中t=182 s時第30層表面縱向殘余應力(σy)的分布曲線.可見，由于熔融金屬不承受負載，所以激光束所達下方應力接近于0.熱膨脹效應使沉積熔池前方即激光束前方存在塑性壓縮區，同時熱收縮效應使沉積熔池后方即激光束后方存在塑性拉伸區.受前一層沉積應力發展的影響，在壓縮區前方存在塑性拉伸區，這些區域被一條從拉伸狀態到壓縮狀態的彈性載荷帶所分割.

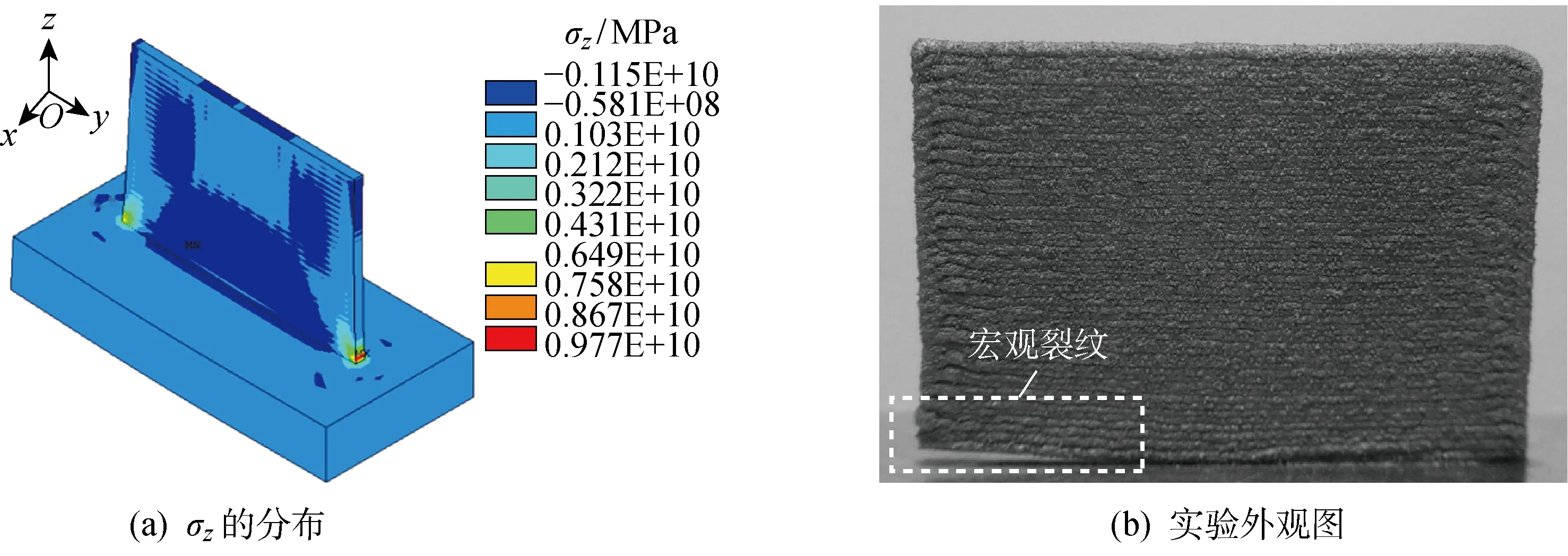
圖7 之字形沉積壁軸向殘余應力σz和實驗外觀圖Fig.7 Axial residual stress σz and experimental appearance of zig-zag deposition wall

圖8 之字形沉積壁殘余應力分布Fig.8 Residual stress distribution of zig-zag depositional wall

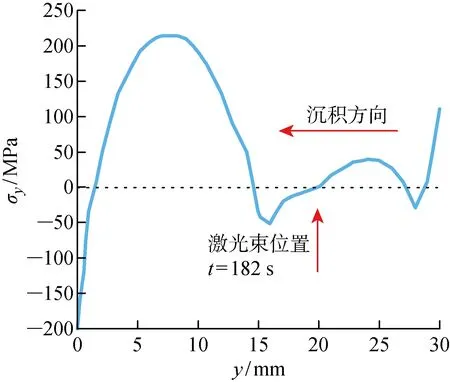
圖6 第30層沿y路徑殘余應力分布曲線Fig.6 Residual stress distribution along the y path in the 30th layer

沉積完成并空冷后，工件所受的不均勻溫度場消失，相應的彈性應力消失，此時所剩的應力即為殘余應力.將數值計算結果與文獻[13]的結果進行對比.之字形沉積壁軸向殘余應力(σz)的分布云圖如圖7(a)所示.可見，沉積壁底部拐角局部出現超過H13工具鋼拉伸強度的拉應力值，驗證了沉積壁拐角出現宏觀裂紋的實驗結果(圖7(b))，裂紋將使鄰近基材沉積壁產生應力松弛.

圖8所示為沿第30層沉積層垂直中心線和水平中心線的殘余應力分量分布曲線，與文獻[16]中的中子衍射殘余應力實驗結果相吻合.文獻[16]的中子衍射殘余應力測量試驗是在不同尺寸(22 mm×1 mm×15 mm)和材料(AISI 410)工件的沉積壁上進行的，在所有代表垂直z方向的橫坐標應力分布圖中均為從自由端指向基材.由圖8(a)可見：σz沿自由端至基材方向增加，σx趨近于為零；在鄰近壁底σy較大，在沉積壁中心收斂為0，說明靠近自由端面的應力在y方向為單軸分布，靠近基材應力分布復雜，σy在沉積壁中心受到自由端和基材的近距離耦合影響.圖8(b)所示的沿水平中心線路徑的應力分布曲線沿y向的拉壓應力分布滿足應力與力矩平衡條件；σz在沉積壁中心主要為壓應力，而在自由邊附近轉變為拉應力，其來源可能為基材剛性約束；拉應力朝基材方向上升，成為部分區域產生裂紋的主要應力來源；而遠離基材自由邊為壓縮應力，這可能是因為沉積過程中受主動力發展的影響(圖6)；當激光束在反向時間點停留時，熱量傳遞至沉積件的深度增加，從而熔池在負z方向上延伸；自由邊緣熔池下方材料受壓縮應力歷程，該處材料不會因激光束反向而產生彈性卸載至拉伸應力狀態.

圖10 單向沉積壁殘余應力σz和實驗外觀圖Fig.10 Residual stress σz and experimental appearance of one-way deposition wall

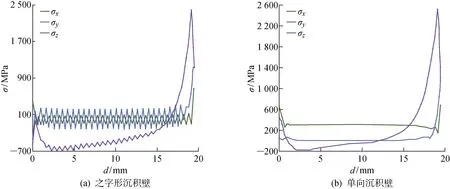
圖11 沿終了自由端殘余應力Fig.11 Residual stress along the ending free edge

圖9所示為之字形沉積壁沿水平中心線的殘余切應力(τxy)分布曲線，可以看出，相鄰兩層的σxy的正負號相反，而在單向沉積壁中則正負號相同，說明沉積路徑影響切應力的發展趨勢.

單向沉積壁沉積過程中，溫度梯度相對較低(圖5)，因此可預測單向沉積壁的殘余應力值低于之字形沉積壁.單向沉積壁殘余應力的分布云圖如圖10(a)所示.沉積壁底部拐角處局部殘余應力高于工件拉伸強度，導致沉積壁底部拐角產生宏觀裂紋，如圖10(b)所示.由于沉積路徑不同，相對垂直中心線的自由邊緣殘余應力不對稱，沉積末端自由邊緣拉應力較高，沿中心層縱向和軸向應力分布與之字形沉積壁應力分布類似.

圖11所示為不同沉積路徑下沉積終了時自由端的殘余應力分布曲線，其中d為測試點距自由端底部的距離.可以看出，之字形沉積壁和單向沉積壁

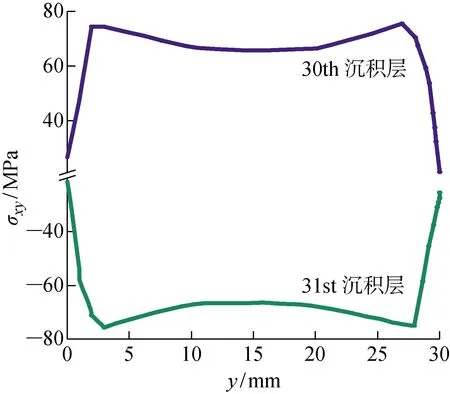
圖9 之字形沉積壁沿水平中心線的σxy分布曲線Fig.9 Distribution curve of σxy for zig-zag deposition wall along horizontal centerline

的應力分布存在差異.其原因為在同一瞬時節點兩者的溫度產生不同程度的波動，單向沉積路徑下的節點溫度梯度變化幅度相對均勻，上升速度緩慢，有利于降低節點溫度峰值及溫度梯度；而采用之字形沉積路徑的節點溫度隨時間呈周期性波動且波動幅值較大，使沉積壁沿終了自由端的殘余應力呈周期性波動.單向沉積路徑無激光束反向，因此z向上殘余壓應力值較低，且各應力分量σx，σy以及σz與σxy均具有相同的正負號.

3 結論

使用有限元分析方法開發了LMD過程的三維熱-力順序耦合模型.主要研究結果如下：

(1) 在直壁結構的近自由邊處存在高拉伸殘余應力，在遠自由邊處存在壓應力.沉積壁和基材之間的殘余應力導致拐角處出現裂紋.

(2) 之字形沉積路徑在沉積層中誘導不同正負號的殘余切應力，單向沉積壁殘余應力略低于之字形沉積壁的殘余應力.

(3) 三維有限元分析有助于識別殘余應力分布，從而確定不同工藝參數對結構關鍵區域的影響，并可優化特定幾何形狀零件的LMD工藝參數.