導(dǎo)數(shù)壓軸題
——零點個數(shù)問題中應(yīng)用零點定理的取值技巧

■王天一

近幾年導(dǎo)數(shù)壓軸題中常出現(xiàn)證明函數(shù)零點個數(shù)或已知零點個數(shù)求參數(shù)范圍的問題。解答這類題的思路主要是結(jié)合函數(shù)的單調(diào)性，應(yīng)用函數(shù)零點定理找出使函數(shù)出現(xiàn)正、負(fù)的函數(shù)值。其中找出符合零點定理成立的恰當(dāng)數(shù)值是順利攻克這類題的難點，下面通過高考經(jīng)典試題例談取值的兩個技巧。

技巧一：簡化運算，恰當(dāng)取值

例題(2019年全國卷Ⅰ)已知函數(shù)f(x)=sinx-ln(1+x)，f'(x)為f(x)的導(dǎo)數(shù)。證明：

(1)f(x)在區(qū)間內(nèi)存在唯一極大值點;

(2)f(x)有且僅有兩個零點。

證明：(1)略。

(2)若f(x)=sinx-ln(1+x)存在零點，需使sinx=ln(1+x)。又x∈(-1，+∞)，sinx∈[-1，1]，則ln(1+x)∈[-1，1]，解得，需證f(x)必須在區(qū)間上存在兩個零點。

f'(x)=cosx-，由(1)及f'(0)=0，可得，可知f'(x)在區(qū)間上存在兩個零點0和x0，其中。當(dāng)時，f'(x)＜0，f(x)單調(diào)遞減;當(dāng)x∈(0，x0)時，f'(x)＞0，f(x)單調(diào)遞增;當(dāng)x∈(x0，e-1)時，f'(x)＜0，f(x)單調(diào)遞減。因為f(0)=0，又f(x0)＞0，f(e-1)=sin(e-1)-lne=sin(e-1)-1＜0，所以f(x)在區(qū)間(x0，e-1)內(nèi)存在唯一零點。

由上述可知，f(x)有且僅有兩個零點。

技巧二：合理待定，放縮估算

例題(2016年全國卷Ⅰ改編)已知a＞0，求證函數(shù)f(x)=(x-2)ex+a(x-1)2有兩個零點。

證明：f'(x)=(x-1)(ex+2a)，當(dāng)a＞0時，f(x)在區(qū)間(-∞，1)上遞減，在區(qū)間(1，+∞)上遞增，所以f(x)min=f(1)=-e＜0。由f(2)=a＞0，可知函數(shù)f(x)在區(qū)間(1，2)內(nèi)有一個零點。觀察可知f(0)＜0，當(dāng)x→-∞時，f(x)→+∞，只需找到一值b，使f(b)＞0，即可證明函數(shù)f(x)有兩個零點。下面運用待定系數(shù)且結(jié)合放縮法找到b的精確值。

由題意可知，需確定的b值比1小，越小越精確，則eb→0。當(dāng)a＞0時，若存在正整數(shù)λ滿足eb＜λa，利于計算，則有f(b)=(b-2)eb+a(b-1)2＞(b-2)λa+a(b-1)2=a[(b-1)2+λ(b-2)]。若(b-1)2+λ(b-2)＞0成立，觀察可知當(dāng)時滿足題意。故取b＜0且時，有2)+a(b-1)2=，如圖1所示。故函數(shù)f(x)在區(qū)間(b，1)和(1，2)內(nèi)各有一個零點。

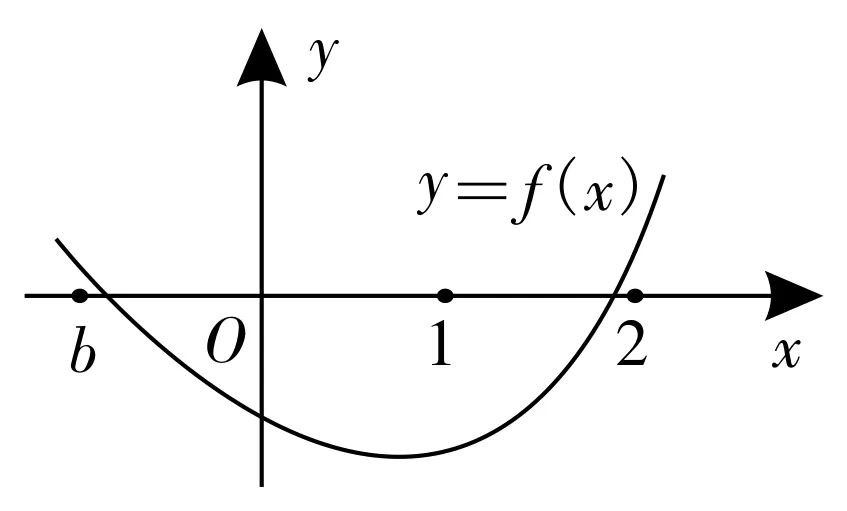
圖1

總結(jié)：以上探究“取值點”的思維過程可以概括為設(shè)出“取值點”，運用分析法，列出不等關(guān)系，將超越不等式通過放縮轉(zhuǎn)化為有理不等式，通過求解或賦值，來不斷探尋式子成立的條件，直到找出合適的數(shù)值。